3.2 : Déterminer des formules empiriques et moléculaires
- Page ID
- 193889
- Calculez la composition en pourcentage d'un composé
- Déterminer la formule empirique d'un composé
- Déterminer la formule moléculaire d'un composé
Dans la section précédente, nous avons discuté de la relation entre la masse apparente d'une substance et le nombre d'atomes ou de molécules qu'elle contient (moles). Compte tenu de la formule chimique de la substance, nous avons pu déterminer la quantité de substance (moles) à partir de sa masse, et vice versa. Mais que se passe-t-il si la formule chimique d'une substance est inconnue ? Dans cette section, nous verrons comment appliquer ces mêmes principes afin de dériver les formules chimiques de substances inconnues à partir de mesures de masse expérimentales.
Composition en pourcentage
La composition élémentaire d'un composé définit son identité chimique, et les formules chimiques constituent la manière la plus succincte de représenter cette composition élémentaire. Lorsque la formule d'un composé est inconnue, la mesure de la masse de chacun de ses éléments constitutifs est souvent la première étape du processus de détermination expérimentale de la formule. Les résultats de ces mesures permettent de calculer la composition en pourcentage du composé, définie comme le pourcentage en masse de chaque élément du composé. Prenons l'exemple d'un composé gazeux composé uniquement de carbone et d'hydrogène. La composition en pourcentage de ce composé peut être représentée comme suit :
\[\mathrm{\%H=\dfrac{mass\: H}{mass\: compound}\times100\%} \nonumber \]
\[\mathrm{\%C=\dfrac{mass\: C}{mass\: compound}\times100\%} \nonumber \]
Si l'analyse d'un échantillon de 10,0 g de ce gaz révélait qu'il contient 2,5 g de H et 7,5 g de C, la composition en pourcentage serait calculée comme étant de 25 % de H et de 75 % de C :
\[\mathrm{\%H=\dfrac{2.5\:g\: H}{10.0\:g\: compound}\times100\%=25\%} \nonumber \]
\[\mathrm{\%C=\dfrac{7.5\:g\: C}{10.0\:g\: compound}\times100\%=75\%} \nonumber \]
L'analyse d'un échantillon de 12,04 g d'un composé liquide composé de carbone, d'hydrogène et d'azote a révélé que ce composé contenait 7,34 g de C, 1,85 g de H et 2,85 g de N. Quelle est la composition en pourcentage de ce composé ?
Solution
Pour calculer la composition en pourcentage, nous divisons la masse dérivée expérimentalement de chaque élément par la masse globale du composé, puis nous la convertissons en pourcentage :
\[\mathrm{\%C=\dfrac{7.34\:g\: C}{12.04\:g\: compound}\times100\%=61.0\%} \nonumber \]
\[\mathrm{\%H=\dfrac{1.85\:g\: H}{12.04\:g\: compound}\times100\%=15.4\%} \nonumber \]
\[\mathrm{\%N=\dfrac{2.85\:g\: N}{12.04\:g\: compound}\times100\%=23.7\%} \nonumber \]
Les résultats de l'analyse indiquent que le composé contient 61,0 % de C, 15,4 % de H et 23,7 % de N en masse.
Un échantillon de 24,81 g d'un composé gazeux contenant uniquement du carbone, de l'oxygène et du chlore est déterminé comme contenant 3,01 g de C, 4,00 g O et 17,81 g de Cl. Quelle est la composition en pourcentage de ce composé ?
- Réponse
-
12,1 % C, 16,1 % O, 71,8 % Cl
Détermination du pourcentage de composition à partir de la masse
La composition en pourcentage est également utile pour évaluer l'abondance relative d'un élément donné dans différents composés de formules connues. Prenons l'exemple des engrais azotés courants tels que l'ammoniac (NH 3), le nitrate d'ammonium (NH 4 NO 3) et l'urée (CH 4 N 2 O). L'élément azote étant l'ingrédient actif utilisé à des fins agricoles, le pourcentage massique d'azote dans le composé est une préoccupation pratique et économique pour les consommateurs qui choisissent parmi ces engrais. Pour ce type d'applications, la composition en pourcentage d'un composé est facilement dérivée de sa masse nominale et des masses atomiques de ses éléments constitutifs. Une molécule de NH 3 contient un atome N pesant 14,01 amu et trois atomes H pesant au total (3 × 1,008 amu) = 3,024 amu. La masse d'ammoniac selon la formule est donc (14,01 amu + 3,024 amu) = 17,03 amu, et sa composition en pourcentage est la suivante :
\[\mathrm{\%N=\dfrac{14.01\:amu\: N}{17.03\:amu\:NH_3}\times100\%=82.27\%} \nonumber \]
\[\mathrm{\%H=\dfrac{3.024\:amu\: N}{17.03\:amu\:NH_3}\times100\%=17.76\%} \nonumber \]
La même approche peut être adoptée en considérant une paire de molécules, une douzaine de molécules ou une mole de molécules, etc. La dernière quantité est la plus pratique et impliquerait simplement l'utilisation de masses molaires au lieu des masses atomiques et des masses de formule, comme le montre l'exemple démontré\(\PageIndex{2}\). Tant que nous connaissons la formule chimique de la substance en question, nous pouvons facilement déduire la composition en pourcentage à partir de la masse de la formule ou de la masse molaire.
L'aspirine est un composé dont la formule moléculaire est C 9 H 8 O 4. Quelle est sa composition en pourcentage ?
Solution
Pour calculer la composition en pourcentage, nous devons connaître les masses de C, H et O dans une masse connue de C 9 H 8 O 4. Il convient de considérer 1 mol de C 9 H 8 O 4 et d'utiliser sa masse molaire (180,159 g/mole, déterminée à partir de la formule chimique) pour calculer les pourcentages de chacun de ses éléments :
\ [\ begin {align*}
\ % \ ce C&= \ mathrm {\ dfrac {9 \ :mol \ : C \ fois molaire \ : masse \ : C} {molaire \ : masse \ : \ ce {C9H18O4}} \ times100= \ dfrac {9 \ times12,01 \ :g/mol} \ nonnumber {180,159 \ :g/mol} \ times 100 = \ dfrac {108,09 \ :g/mol} {180,159 \ :g/mol} \ fois100} \ nonnumber \ \
\ % \ ce C&= \ mathrm {60,00 \, \ % \, C} \ nonnumber
\ end {align*} \ nonumber \]
\ [\ begin {align*}
\ % \ ce H&= \ mathrm {\ dfrac {8 \ :mol \ : H \ fois molaire \ : masse \ : H} {molaire \ : masse \ : \ ce {C9H18O4}} \ fois 100= \ dfrac {8 \ fois 1,008 \ :g/mol} \ fois 100 = \ dfrac {8,064 \ :g/mol} {180,159 \ :g/mol} \ fois 100} \ nonnumber \ \ \ %
\ ce H&=4,476 \, \ % \, \ ce H \ nonnumber
\ end {align*} \ nonumber \]
\ [\ begin {align*}
\ % \ ce O&= \ mathrm {\ dfrac {4 \ :mol \ : O \ fois molaire \ : masse \ : O} {molaire \ : masse \ : \ ce {C9H18O4}} \ fois 100= \ dfrac {4 \ fois 16,00 \ :g/mol} \ nonnumber {180,159 \ :g/mol} \ fois 100 = \ dfrac {64,00 \ :g/mol} {180,159 \ :g/mol} \ fois 100} \ nonnumber \ \
\ % \ ce O&=35,52 \ % \ nonnumber
\ end {align*} \ nonumber \]
Notez que la somme de ces pourcentages est égale à 100,00 % lorsqu'elle est arrondie de manière appropriée.
À trois chiffres significatifs, quel est le pourcentage massique de fer dans le composé\(Fe_2O_3\) ?
- Réponse
-
69,9 % Fe
Détermination des formules empiriques
Comme indiqué précédemment, l'approche la plus courante pour déterminer la formule chimique d'un composé consiste à mesurer d'abord les masses de ses éléments constitutifs. Cependant, nous devons garder à l'esprit que les formules chimiques représentent les nombres relatifs, et non les masses, des atomes de la substance. Par conséquent, toutes les données expérimentales concernant la masse doivent être utilisées pour dériver le nombre correspondant d'atomes dans le composé. Pour ce faire, nous pouvons utiliser des masses molaires pour convertir la masse de chaque élément en un nombre de moles. Nous examinons ensuite les moles de chaque élément les uns par rapport aux autres, en convertissant ces nombres en un ratio de nombres entiers qui peut être utilisé pour dériver la formule empirique de la substance. Considérons un échantillon de composé dont on a déterminé qu'il contient 1,71 g de C et 0,287 g de H. Les nombres d'atomes correspondants (en moles) sont les suivants :
\[\mathrm{1.71\:g\: C\times \dfrac{1\:mol\: C}{12.01\:g\: C}=0.142\:mol\: C} \nonumber \]
\[\mathrm{0.287\:g\: H\times \dfrac{1\:mol\: H}{1.008\:g\: H}=0.284\:mol\: H} \nonumber \]
Ainsi, nous pouvons représenter avec précision ce composé avec la formule C 0,142 H 0,284. Bien entendu, selon la convention acceptée, les formules contiennent des indices entiers, qui peuvent être obtenus en divisant chaque indice par le plus petit indice :
\[\ce C_{\Large{\frac{0.142}{0.142}}}\:\ce H_{\Large{\frac{0.284}{0.142}}}\ce{\:or\:CH2} \nonumber \]
(Rappelez-vous que les indices de « 1 » ne sont pas écrits, mais supposés si aucun autre nombre n'est présent.)
La formule empirique de ce composé est donc le CH 2. Il peut s'agir ou non de la formule moléculaire du composé ; toutefois, nous aurions besoin d'informations supplémentaires pour effectuer cette détermination (comme indiqué plus loin dans cette section).
Prenons comme autre exemple un échantillon d'un composé dont il a été déterminé qu'il contient 5,31 g de Cl et 8,40 g d'O. En suivant la même approche, on obtient une formule empirique provisoire de :
\[\mathrm{Cl_{0.150}O_{0.525}=Cl_{\Large{\frac{0.150}{0.150}}}\: O_{\Large{\frac{0.525}{0.150}}}=ClO_{3.5}} \nonumber \]
Dans ce cas, la division par le plus petit indice nous laisse toujours un indice décimal dans la formule empirique. Pour convertir cela en un nombre entier, nous devons multiplier chacun des indices par deux, en conservant le même rapport atomique et en obtenant Cl 2 O 7 comme formule empirique finale.
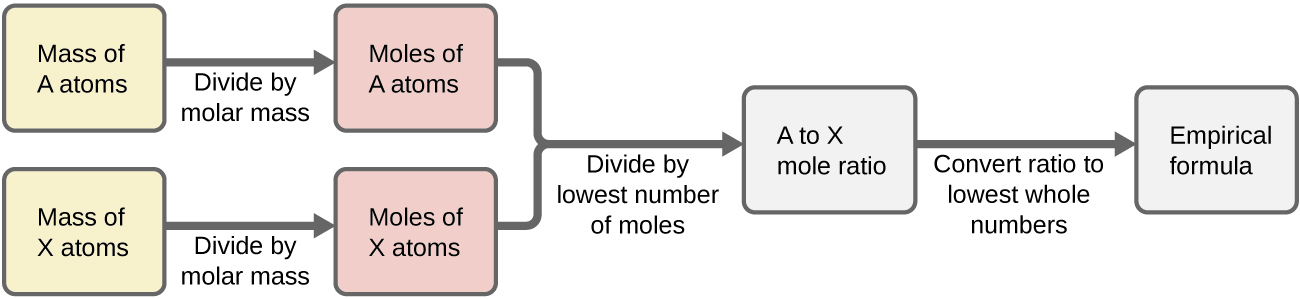
En résumé, les formules empiriques sont dérivées des masses d'éléments mesurées expérimentalement par :
- Dériver le nombre de moles de chaque élément à partir de sa masse
- Diviser la quantité molaire de chaque élément par la plus petite quantité molaire pour obtenir des indices pour une formule empirique provisoire
- Multiplier tous les coefficients par un entier, si nécessaire, pour obtenir le plus petit rapport d'indices entre nombres entiers
La figure\(\PageIndex{1}\) décrit cette procédure sous forme d'organigramme pour une substance contenant les éléments A et X.
Un échantillon d'hématite minérale noire (Figure\(\PageIndex{2}\)), un oxyde de fer présent dans de nombreux minerais de fer, contient 34,97 g de fer et 15,03 g d'oxygène. Quelle est la formule empirique de l'hématite ?

Solution
Pour ce problème, on nous donne la masse en grammes de chaque élément. Commencez par trouver les taupes de chacun :
\ [\ begin {align*}
\ mathrm {34,97 \ :g \ : Fe \ left (\ dfrac {mol \ : Fe} {55,85 \ :g} \ right)} &= \ mathrm {0,6261 \ :mol \ : Fe} \ nonnumber \ \ \ nonumber \ \
\ mathrm {15.03 \ :g \ : O \ left (\ dfrac {mol \ : O} {16.00 \ :g} \ right)} &= \ mathrm {0,9394 \ :mol \ : O} \ nonumber
\ end {align*} \ nonnumber \]
Ensuite, déterminez le rapport molaire fer/oxygène en divisant par le plus petit nombre de moles :
\[\mathrm{\dfrac{0.6261}{0.6261}=1.000\:mol\: Fe} \nonumber \]
\[\mathrm{\dfrac{0.9394}{0.6261}=1.500\:mol\: O} \nonumber \]
Le rapport est de 1 000 moles de fer pour 1 500 moles d'oxygène (Fe 1 O 1,5). Enfin, multipliez le ratio par deux pour obtenir le plus petit indice entier possible tout en maintenant le bon rapport fer/oxygène :
\[\mathrm{2(Fe_1O_{1.5})=Fe_2O_3} \nonumber \]
La formule empirique est\(Fe_2O_3\).
Quelle est la formule empirique d'un composé si un échantillon contient 0,130 g d'azote et 0,370 g d'oxygène ?
- Réponse
-
\(N_2O_5\)
Vidéo\(\PageIndex{1}\) : D'autres exemples pratiques illustrant la dérivation de formules empiriques sont présentés dans le bref clip vidéo.
Dériver des formules empiriques à partir de la
Enfin, en ce qui concerne la dérivation de formules empiriques, considérez les cas dans lesquels la composition en pourcentage d'un composé est disponible plutôt que les masses absolues des éléments constitutifs du composé. Dans de tels cas, la composition en pourcentage peut être utilisée pour calculer les masses d'éléments présents dans n'importe quelle masse appropriée de composé ; ces masses peuvent ensuite être utilisées pour dériver la formule empirique de la manière habituelle.
La fermentation bactérienne du grain pour produire de l'éthanol forme un gaz dont la composition en pourcentage est de 27,29 % de C et de 72,71 % d'O (Figure\(\PageIndex{3}\)). Quelle est la formule empirique de ce gaz ?

Solution
Comme l'échelle des pourcentages est de 100, il est plus pratique de calculer la masse des éléments présents dans un échantillon pesant 100 g. Le calcul est « très pratique » car, selon la définition de la composition en pourcentage, la masse d'un élément donné en grammes est numériquement équivalente à la masse de l'élément pourcentage. Cette équivalence numérique résulte de la définition de l'unité « pourcentage », dont le nom est dérivé de l'expression latine per centum qui signifie « par cent ». Compte tenu de cette définition, les pourcentages massiques fournis peuvent être plus facilement exprimés en fractions :
\ [\ begin {align*}
27,29 \, \ % \, \ ce C&= \ mathrm {\ dfrac {27.29 \ :g \ : C} {100 \ :g \ : composé}} \ nonnumber \ \ \ 72,71 \, \ % \, \ ce O&= \ mathrm {\ dfrac {
72.71 \ :g \ : O} {100 \ % \, \ ce O&= \ mathrm {72,71 \ :g \ : O} {100 \ \ :g \ : composé}}
\ nonumber \ end {align*} \ nonnumber \]
Les quantités molaires de carbone et d'hydrogène dans un échantillon de 100 g sont calculées en divisant la masse de chaque élément par sa masse molaire :
\ [\ begin {align*}
\ mathrm {27,29 \ :g \ : C \ left (\ dfrac {mol \ : C} {12,01 \ :g} \ right)} &= \ mathrm {2,272 \ :mol \ : C} \ nonnumber \ \ \ nonnumber \ \
\ mathrm {72.71 \ :g \ : O \ left (\ dfrac {mol \ : O} {16.00 \ :g} \ right)} &= \ mathrm {4.544 \ :mol \ : O} \ nonumber
\ end {align*} \ nonnumber \]
Les coefficients de la formule empirique provisoire sont obtenus en divisant chaque quantité molaire par la plus faible des deux valeurs suivantes :
\[\mathrm{\dfrac{2.272\:mol\: C}{2.272}=1} \nonumber \]
\[\mathrm{\dfrac{4.544\:mol\: O}{2.272}=2} \nonumber \]
Comme le rapport obtenu est d'un atome de carbone pour deux atomes d'oxygène, la formule empirique est CO 2.
Quelle est la formule empirique d'un composé contenant 40,0 % de C, 6,71 % de H et 53,28 % de O ?
- Réponse
-
\(CH_2O\)
Dérivation de formules moléculaires
Rappelons que les formules empiriques sont des symboles représentant le nombre relatif des éléments d'un composé. Pour déterminer le nombre absolu d'atomes qui composent une seule molécule d'un composé covalent, il faut connaître à la fois sa formule empirique et sa masse moléculaire ou masse molaire. Ces quantités peuvent être déterminées expérimentalement par différentes techniques de mesure. La masse moléculaire, par exemple, est souvent dérivée du spectre de masse du composé (voir la discussion de cette technique dans le chapitre précédent sur les atomes et les molécules). La masse molaire peut être mesurée par un certain nombre de méthodes expérimentales, dont beaucoup seront présentées dans les chapitres suivants de ce texte.
Les formules moléculaires sont dérivées en comparant la masse moléculaire ou molaire du composé à sa masse de formule empirique. Comme son nom l'indique, la masse d'une formule empirique est la somme des masses atomiques moyennes de tous les atomes représentés dans une formule empirique. Si nous connaissons la masse moléculaire (ou molaire) de la substance, nous pouvons la diviser par la masse de la formule empirique afin d'identifier le nombre d'unités de formule empirique par molécule, que nous désignons par n :
\[\mathrm{\dfrac{molecular\: or\: molar\: mass\left(amu\: or\:\dfrac{g}{mol}\right)}{empirical\: formula\: mass\left(amu\: or\:\dfrac{g}{mol}\right)}= \mathit n\: formula\: units/molecule} \nonumber \]
La formule moléculaire est ensuite obtenue en multipliant chaque indice de la formule empirique par n, comme le montre la formule empirique générique A x B y :
\[\mathrm{(A_xB_y)_n=A_{nx}B_{nx}} \nonumber \]
Prenons l'exemple d'un composé covalent dont la formule empirique est déterminée comme étant le CH 2 O. La masse de la formule empirique pour ce composé est d'environ 30 amu (la somme de 12 amu pour un atome de C, de 2 amu pour deux atomes de H et de 16 amu pour un atome d'O). Si la masse moléculaire du composé est déterminée à 180 amu, cela indique que les molécules de ce composé contiennent six fois le nombre d'atomes représentés dans la formule empirique :
\[\mathrm{\dfrac{180\:amu/molecule}{30\:\dfrac{amu}{formula\: unit}}=6\:formula\: units/molecule} \nonumber \]
Les molécules de ce composé sont alors représentées par des formules moléculaires dont les indices sont six fois supérieurs à ceux de la formule empirique :
\[\ce{(CH2O)6}=\ce{C6H12O6} \nonumber \]
Notez que cette même approche peut être utilisée lorsque la masse molaire (g/mol) au lieu de la masse moléculaire (amu) est utilisée. Dans ce cas, nous considérons simplement une mole d'unités et de molécules de formule empirique, par opposition à des unités et des molécules uniques.
La nicotine, un alcaloïde de la famille des morelles qui est principalement responsable de la dépendance des cigarettes, contient 74,02 % de C, 8,710 % de H et 17,27 % de N. Si 40,57 g de nicotine contiennent 0,2500 mol de nicotine, quelle est la formule moléculaire ?
Solution
Pour déterminer la formule moléculaire à partir des données fournies, il faudra comparer la masse de formule empirique du composé à sa masse molaire. Dans un premier temps, utilisez la composition en pourcentage pour obtenir la formule empirique du composé. En supposant que cela soit pratique, un échantillon de 100 g de nicotine produit les quantités molaires suivantes de ses éléments :
\ [\ begin {alignat} {2}
& \ mathrm {(74,02 \ :g \ : C) \ left (\ dfrac {1 \ :mol \ : C} {12,01 \ :g \ : C} \ right)} &= \ : \ mathrm {6,163 \ :mol \ : C} \ \
& \ mathrm {(8,710 \ :g \ : H) left (\ dfrac {1 \ :mol \ : H} {1,01 \ :g \ : H} \ right)} &= \ : \ mathrm {8,624 \ :mol \ : H} \ \
& \ mathrm {(17,27 \ :g \ : N) \ left (\ dfrac {1 \ :mol \ : N} {14.01 \ :g \ : N} \ right)} &= \ : \ mathrm {1,233 \ :mol \ : N}
\ end {alignat} \ nonnumber \]
Ensuite, nous calculons les rapports molaires de ces éléments par rapport à l'élément le moins abondant,\(\ce{N}\).
\(6.163 \: \text{mol} \: \ce{C}\)/\(1.233 \: \text{mol} \: \ce{N}\)= 5
\(8.264 \: \text{mol} \: \ce{H}\)/\(1.233 \: \text{mol} \: \ce{N}\)= 7
\(1.233 \: \text{mol} \: \ce{N}\)/\(1.233\: \text{mol} \: \ce{N}\)= 1
1,233 = 1,233 =\(1.000 \: \text{mol} \: \ce{N}\)
6,163 =\(4.998 \: \text{mol} \: \ce{C}\)
8,624/1,233 =\(6.994 \: \text{mol} \: \ce{H}\)
Les rapports molaires C-N et H-to-N étant suffisamment proches des nombres entiers, la formule empirique est C 5 H 7 N. La masse de la formule empirique pour ce composé est donc de 81,13 amu/unité de formule, soit 81,13 g/mol unité de formule.
Nous calculons la masse molaire de la nicotine à partir de la masse et de la quantité molaire de composé données :
\[\mathrm{\dfrac{40.57\:g\: nicotine}{0.2500\:mol\: nicotine}=\dfrac{162.3\:g}{mol}} \nonumber \]
La comparaison de la masse molaire et de la masse de la formule empirique indique que chaque molécule de nicotine contient deux unités de formule :
\[\mathrm{\dfrac{162.3\:g/mol}{81.13\:\dfrac{g}{formula\: unit}}=2\:formula\: units/molecule} \nonumber \]
Ainsi, nous pouvons déduire la formule moléculaire de la nicotine à partir de la formule empirique en multipliant chaque indice par deux :
\[\ce{(C5H7N)2}=\ce{C10H14N2} \nonumber \]
Quelle est la formule moléculaire d'un composé dont la composition en pourcentage est de 49,47 % de C, 5,201 % de H, 28,84 % de N et 16,48 % O, et dont la masse moléculaire est de 194,2 amu ?
- Réponse
-
C 8 H 10 N 4 O 2
Résumé
L'identité chimique d'une substance est définie par les types et le nombre relatif d'atomes composant ses entités fondamentales (molécules dans le cas des composés covalents, ions dans le cas des composés ioniques). La composition en pourcentage d'un composé fournit le pourcentage massique de chaque élément du composé, et elle est souvent déterminée expérimentalement et utilisée pour dériver la formule empirique du composé. La masse de formule empirique d'un composé covalent peut être comparée à la masse moléculaire ou molaire du composé pour obtenir une formule moléculaire.
Équations clés
- \(\mathrm{\%X=\dfrac{mass\: X}{mass\: compound}\times100\%}\)
- \(\mathrm{\dfrac{molecular\: or\: molar\: mass\left(amu\: or\:\dfrac{g}{mol}\right)}{empirical\: formula\: mass\left(amu\: or\:\dfrac{g}{mol}\right)}=\mathit n\: formula\: units/molecule}\)
- (A x B y) n = A x B ny
Lexique
- composition en pourcentage
- pourcentage en masse des différents éléments d'un composé
- masse de formule empirique
- somme des masses atomiques moyennes pour tous les atomes représentés dans une formule empirique


