Skip to main content
Global

Chapitre 11 Exercices de révision

  1. Last updated
  2. Save as PDF
  • Page ID
    194498

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Exercices de révision des

    Formules de distance et de point médian ; cercles

    Exercice\(\PageIndex{1}\) Use the Distance Formula

    Dans les exercices suivants, déterminez la distance entre les points. Si nécessaire, arrondissez au dixième le plus proche.

    1. \((-5,1)\)et\((-1,4)\)
    2. \((-2,5)\)et\((1,5)\)
    3. \((8,2)\)et\((-7,-3)\)
    4. \((1,-4)\)et\((5,-5)\)
    Réponse

    2. \(d=3\)

    4. \(d=\sqrt{17}, d \approx 4.1\)

    Exercice\(\PageIndex{2}\) Use the Midpoint Formula

    Dans les exercices suivants, trouvez le milieu des segments de ligne dont les extrémités sont indiquées.

    1. \((-2,-6)\)et\((-4,-2)\)
    2. \((3,7)\)et\((5,1)\)
    3. \((-8,-10)\)et\((9,5)\)
    4. \((-3,2)\)et\((6,-9)\)
    Réponse

    2. \((4,4)\)

    4. \(\left(\frac{3}{2},-\frac{7}{2}\right)\)

    Exercice\(\PageIndex{3}\) Write the Equation of a Circle in Standard Form

    Dans les exercices suivants, écrivez la forme standard de l'équation du cercle avec les informations données.

    1. le rayon est\(15\) et le centre est\((0,0)\)
    2. le rayon est\(\sqrt{7}\) et le centre est\((0,0)\)
    3. le rayon est\(9\) et le centre est\((-3,5)\)
    4. le rayon est\(7\) et le centre est\((-2,-5)\)
    5. le centre est\((3,6)\) et un point du cercle est\((3,-2)\)
    6. le centre est\((2,2)\) et un point du cercle est\((4,4)\)
    Réponse

    2. \(x^{2}+y^{2}=7\)

    4. \((x+2)^{2}+(y+5)^{2}=49\)

    6. \((x-2)^{2}+(y-2)^{2}=8\)

    Exercice\(\PageIndex{4}\) Graph a Circle

    Dans les exercices suivants,

    1. Trouvez le centre et le rayon, puis
    2. Tracez chaque cercle.
    1. \(2 x^{2}+2 y^{2}=450\)
    2. \(3 x^{2}+3 y^{2}=432\)
    3. \((x+3)^{2}+(y-5)^{2}=81\)
    4. \((x+2)^{2}+(y+5)^{2}=49\)
    5. \(x^{2}+y^{2}-6 x-12 y-19=0\)
    6. \(x^{2}+y^{2}-4 y-60=0\)
    Réponse

    2.

    1. rayon :\(12,\) centre :\((0,0)\)
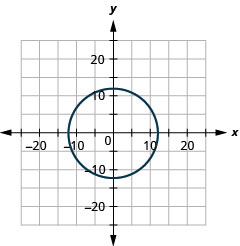
    La figure montre un cercle tracé sur le plan de coordonnées x y. L'axe X du plan va de moins 20 à 20. L'axe Y du plan va de moins 15 à 15. Le centre du cercle est (0, 0) et le rayon du cercle est 12.
    Figure 11.E.1

    4.

    1. rayon :\(7,\) centre :\((-2,-5)\)
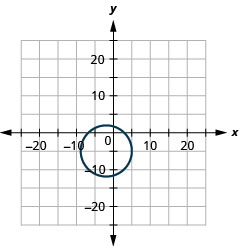
    La figure montre un cercle tracé sur le plan de coordonnées x y. L'axe X du plan va de moins 20 à 20. L'axe Y du plan va de moins 15 à 15. Le centre du cercle est (moins 2, moins 5) et le rayon du cercle est 7.
    Figure 11.E.2

    6.

    1. rayon :\(8,\) centre :\((0,2)\)
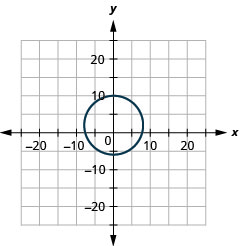
    La figure montre un cercle tracé sur le plan de coordonnées x y. L'axe X du plan va de moins 20 à 20. L'axe Y du plan va de moins 15 à 15. Le centre du cercle est (0, 2) et le rayon du cercle est 8.
    Figure 11.E.3

    Paraboles

    Exercice\(\PageIndex{5}\) Graph Vertical Parabolas

    Dans les exercices suivants, tracez chaque équation à l'aide de ses propriétés.

    1. \(y=x^{2}+4 x-3\)
    2. \(y=2 x^{2}+10 x+7\)
    3. \(y=-6 x^{2}+12 x-1\)
    4. \(y=-x^{2}+10 x\)
    Réponse

    2.

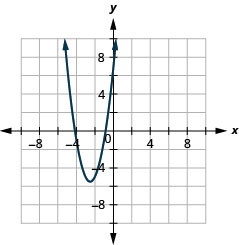
    La figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 7 à 7. Le sommet est (moins cinq moitiés, moins onze moitiés) et la parabole passe par les points (négatif 4, négatif 1) et (négatif 1, négatif 1).
    Figure 11.E.4

    4.

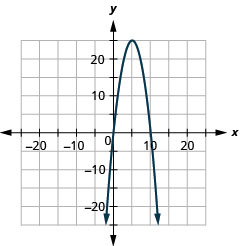
    La figure montre une parabole s'ouvrant vers le bas tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 36 à 36. L'axe Y du plan va de moins 26 à 26. Le sommet est (5, 25) et la parabole passe par les points (2, 16) et (8, 16).
    Figure 11.E.5
    Exercice\(\PageIndex{6}\) Graph Vertical Parabolas

    Dans les exercices suivants,

    1. Écrivez l'équation sous forme standard, puis
    2. Utilisez les propriétés du formulaire standard pour représenter graphiquement l'équation.
    1. \(y=x^{2}+4 x+7\)
    2. \(y=2 x^{2}-4 x-2\)
    3. \(y=-3 x^{2}-18 x-29\)
    4. \(y=-x^{2}+12 x-35\)
    Réponse

    2.

    1. \(y=2(x-1)^{2}-4\)
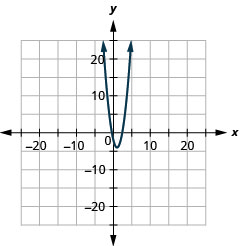
    La figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 22 à 22. L'axe Y du plan va de moins 16 à 16. Le sommet est (1, négatif 4) et la parabole passe par les points (0, moins 2) et (2, moins 2).
    Figure 11.E.6

    4.

    1. \(y=-(x-6)^{2}+1\)
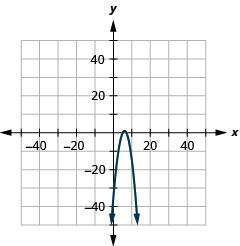
    La figure montre une parabole s'ouvrant vers le bas tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 60 à 60. L'axe Y du plan va de moins 46 à 46. Le sommet est (6, 1) et la parabole passe par les points (5, 0) et (7, 0).
    Figure 11.E.7
    Exercice\(\PageIndex{7}\) Graph Horizontal Parabolas

    Dans les exercices suivants, tracez chaque équation à l'aide de ses propriétés.

    1. \(x=2 y^{2}\)
    2. \(x=2 y^{2}+4 y+6\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(x=-3 y^{2}\)
    Réponse

    2.

    La figure montre une parabole s'ouvrant vers la droite tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 8 à 8. Le sommet est (4, négatif 1) et la parabole passe par les points (6, 0) et (6, négatif 2).
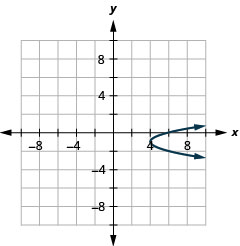
    Figure 11.E.8

    4.

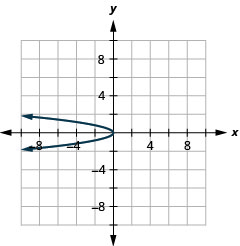
    La figure montre une parabole s'ouvrant vers la gauche tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 8 à 8. Le sommet est (0, 0) et la parabole passe par les points (négatif 3, 1) et (négatif 3, négatif 1).
    Figure 11.E.9
    Exercice\(\PageIndex{8}\) Graph Horizontal Parabolas

    Dans les exercices suivants,

    1. Écrivez l'équation sous forme standard, puis
    2. Utilisez les propriétés du formulaire standard pour représenter graphiquement l'équation.
    1. \(x=4 y^{2}+8 y\)
    2. \(x=y^{2}+4 y+5\)
    3. \(x=-y^{2}-6 y-7\)
    4. \(x=-2 y^{2}+4 y\)
    Réponse

    2.

    1. \(x=(y+2)^{2}+1\)
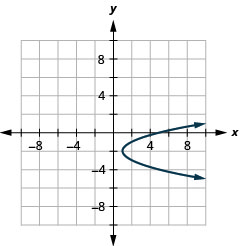
    La figure montre une parabole s'ouvrant vers la droite tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 8 à 8. Le sommet est (1, négatif 2) et la parabole passe par les points (5, 0) et (5, moins 4).
    Figure 11.E.10

    4.

    1. \(x=-2(y-1)^{2}+2\)
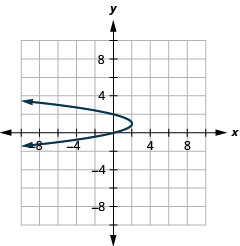
    La figure montre une parabole s'ouvrant vers la gauche tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 8 à 8. Le sommet est (2, négatif 3) et la parabole passe par les points (0, 2) et (0, 0).
    Figure 11.E.11
    Exercice\(\PageIndex{9}\) Solve Applications with Parabolas

    Dans les exercices suivants, créez l'équation de l'arc parabolique formé dans la fondation du pont illustré. Donnez la réponse sous une forme standard.

    1.

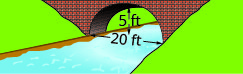
    La figure montre un arc parabolique formé dans les fondations du pont. L'arche mesure 5 pieds de haut et 20 pieds de large.
    Figure 11.E.12

    2.

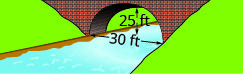
    La figure montre un arc parabolique formé dans les fondations du pont. L'arche mesure 25 pieds de haut et 30 pieds de large.
    Figure 11.E.13
    Réponse

    2. \(y=-\frac{1}{9} x^{2}+\frac{10}{3} x\)

    Ellipses

    Exercice\(\PageIndex{10}\) Graph an Ellipse with Center at the Origin

    Dans les exercices suivants, tracez chaque ellipse.

    1. \(\frac{x^{2}}{36}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{4}+\frac{y^{2}}{81}=1\)
    3. \(49 x^{2}+64 y^{2}=3136\)
    4. \(9 x^{2}+y^{2}=9\)
    Réponse

    2.

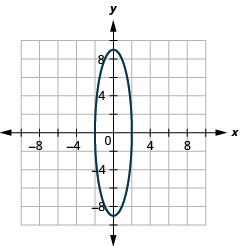
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'ellipse possède un centre à (0, 0), un grand axe vertical, des sommets à (0, plus ou moins 9) et des co-sommets à (plus ou moins 2, 0).
    Figure 11.E.14

    4.

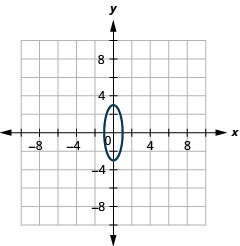
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 9 à 9. L'axe Y du plan va de moins 7 à 7. L'ellipse possède un centre à (0, 0), un grand axe vertical, des sommets à (0, plus ou moins 3) et des co-sommets à (plus ou moins 1, 0).
    Figure 11.E.15
    Exercice\(\PageIndex{11}\) Find the Equation of an Ellipse with Center at the Origin

    Dans les exercices suivants, trouvez l'équation de l'ellipse illustrée sur le graphique.

    1.

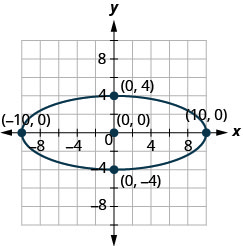
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'ellipse possède un centre à (0, 0), un axe principal horizontal, des sommets à (plus ou moins 10, 0) et des co-sommets à (0, plus ou moins 4).
    Figure 11.E.16

    2.

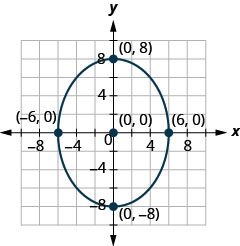
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'ellipse possède un centre à (0, 0), un grand axe vertical, des sommets à (0, plus ou moins 8) et des co-sommets à (plus ou moins 6, 0).
    Figure 11.E.17
    Réponse

    2. \(\frac{x^{2}}{36}+\frac{y^{2}}{64}=1\)

    Exercice\(\PageIndex{12}\) Graph an Ellipse with Center Not at the Origin

    Dans les exercices suivants, tracez chaque ellipse.

    1. \(\frac{(x-1)^{2}}{25}+\frac{(y-6)^{2}}{4}=1\)
    2. \(\frac{(x+4)^{2}}{16}+\frac{(y+1)^{2}}{9}=1\)
    3. \(\frac{(x-5)^{2}}{16}+\frac{(y+3)^{2}}{36}=1\)
    4. \(\frac{(x+3)^{2}}{9}+\frac{(y-2)^{2}}{25}=1\)
    Réponse

    2.

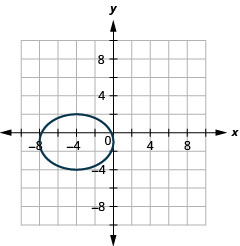
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'ellipse possède un centre en (négatif 4, négatif 1), un axe principal horizontal, des sommets en (négatif 8, négatif 1) et (0, négatif 1) et des co-sommets en (négatif 4, 2) et (négatif 4, négatif 4).
    Figure 11.E.18

    4.

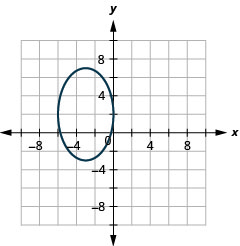
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'ellipse possède un centre en (négatif 3, 2), un grand axe vertical, des sommets en (négatif 3, 7) et (négatif 3, moins 3) et des co-sommets en (négatif 6, 2) et (0, 2).
    Figure 11.E.19
    Exercice\(\PageIndex{13}\) Graph an Ellipse with Center Not at the Origin

    Dans les exercices suivants,

    1. Écrivez l'équation sous forme standard et
    2. Graphe.
    1. \(x^{2}+y^{2}+12 x+40 y+120=0\)
    2. \(25 x^{2}+4 y^{2}-150 x-56 y+321=0\)
    3. \(25 x^{2}+4 y^{2}+150 x+125=0\)
    4. \(4 x^{2}+9 y^{2}-126 x+405=0\)
    Réponse

    2.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
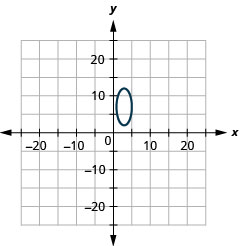
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 18 à 18. L'axe Y du plan va de moins 14 à 14. L'ellipse possède un centre en (3, 7), un grand axe vertical, des sommets en (3, 2) et (3, 12) et des co-sommets en (moins 1, 7) et (5, 7).
    Figure 11.E.20

    4.

    1. \(\frac{x^{2}}{9}+\frac{(y-7)^{2}}{4}=1\)
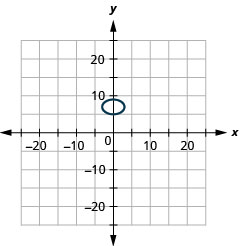
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 15 à 15. L'axe Y du plan va de moins 11 à 11. L'ellipse possède un centre en (0, 7), un axe principal horizontal, des sommets en (3, 7) et (moins 3, 7) et des co-sommets en (0, 5) et (0, 9).
    Figure 11.E.21
    Exercice\(\PageIndex{14}\) Solve Applications with Ellipses

    Dans les exercices suivants, écrivez l'équation de l'ellipse décrite.

    1. Une comète se déplace sur une orbite elliptique autour du soleil. La comète se rapproche le plus du soleil approximativement\(10\) au et la plus éloignée se trouve à peu près\(90\) au UA. Le soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de la comète.
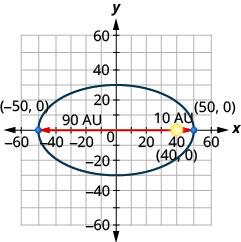
    La figure montre un modèle d'une orbite elliptique autour du soleil sur le plan de coordonnées x y. L'ellipse a un centre en (0, 0), un grand axe horizontal, des sommets marqués à (plus ou moins 50, 0), le soleil marqué comme foyer et étiqueté (50, 0), la distance la plus proche entre la comète et le soleil est marquée par 10 A U, et la plus éloignée d'une comète est marquée par 90 A U.
    Figure 11.E.22
    Réponse

    1. Résoudre

    Hyperboles

    Exercice\(\PageIndex{15}\) Graph a Hyperbola with Center at \((0,0)\)

    Dans les exercices suivants, tracez un graphique.

    1. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    2. \(\frac{y^{2}}{49}-\frac{x^{2}}{16}=1\)
    3. \(9 y^{2}-16 x^{2}=144\)
    4. \(16 x^{2}-4 y^{2}=64\)
    Réponse

    1.

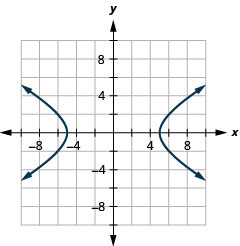
    La figure montre une hyperbole tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 12 à 12. L'axe Y du plan va de moins 9 à 9. L'hyperbole a un centre en (0, 0) et des branches qui passent par les sommets (plus ou moins 5, 0) et qui s'ouvrent à gauche et à droite.
    Figure 11.E.23

    3.

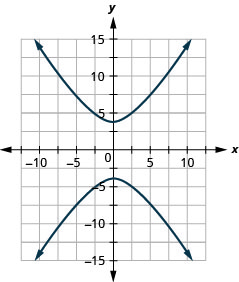
    La figure montre une hyperbole tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 19 à 19. L'axe Y du plan va de moins 15 à 15. L'hyperbole a un centre en (0, 0) et des branches qui passent par les sommets (0, plus ou moins 4) et qui s'ouvrent de haut en bas.
    Figure 11.E.24
    Exercice\(\PageIndex{16}\) Graph a Hyperbola with Center at \((h,k)\)

    Dans les exercices suivants, tracez un graphique.

    1. \(\frac{(x+1)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{9}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-2)^{2}}{9}=1\)
    Réponse

    1.

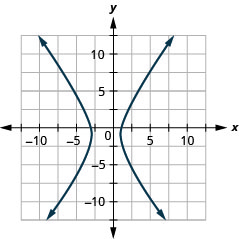
    La figure montre une hyperbole tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'hyperbole a un centre en (négatif 1, moins 1) et des branches qui passent par les sommets (négatif 3, négatif 1) et (1, négatif 1), et qui s'ouvrent à gauche et à droite.
    Figure 11.E.25

    3.

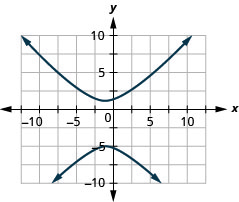
    La figure montre une hyperbole tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'hyperbole a un centre en (négatif 1, moins 2) et des branches qui passent par les sommets (négatif 1, 1) et (négatif 1, négatif 5), et qui s'ouvrent de haut en bas.
    Figure 11.E.26
    Exercice\(\PageIndex{17}\) Graph a Hyperbola with Center at \((h,k)\)

    Dans les exercices suivants,

    1. Écrivez l'équation sous forme standard et
    2. Graphe.
    1. \(4 x^{2}-16 y^{2}+8 x+96 y-204=0\)
    2. \(16 x^{2}-4 y^{2}-64 x-24 y-36=0\)
    3. \(4 y^{2}-16 x^{2}+32 x-8 y-76=0\)
    4. \(36 y^{2}-16 x^{2}-96 x+216 y-396=0\)
    Réponse

    1.

    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
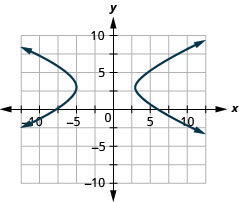
    La figure montre une hyperbole tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'hyperbole a un centre en (négatif 1, 3) et des branches qui passent par les sommets (négatif 5, 3) et (3, 3), et qui s'ouvrent à gauche et à droite.
    Figure 11.E.27

    3.

    1. \(\frac{(y-1)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)
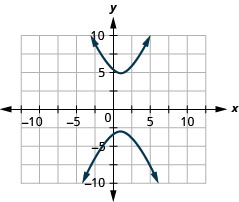
    La figure montre une hyperbole tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'hyperbole a un centre en (1, 1) et des branches qui passent par les sommets (1, moins 3) et (1, 5), et qui s'ouvrent de haut en bas.
    Figure 11.E.28
    Exercice\(\PageIndex{18}\) Identify the Graph of Each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    Dans les exercices suivants, identifiez le type de graphique.

      1. \(16 y^{2}-9 x^{2}-36 x-96 y-36=0\)
      2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      3. \(y=x^{2}-2 x+3\)
      4. \(25 x^{2}+9 y^{2}=225\)
      1. \(x^{2}+y^{2}+4 x-10 y+25=0\)
      2. \(y^{2}-x^{2}-4 y+2 x-6=0\)
      3. \(x=-y^{2}-2 y+3\)
      4. \(16 x^{2}+9 y^{2}=144\)
    Réponse

    1.

    1. Hyperbole
    2. cercle
    3. Parabole
    4. Ellipse

    Résoudre des systèmes d'équations non linéaires

    Exercice\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Graphing

    Dans les exercices suivants, résolvez le système d'équations à l'aide de graphiques.

    1. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y=-5}\end{array}\right.\)
    Réponse

    1.

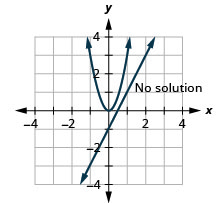
    La figure montre une parabole et une ligne tracées sur le plan de coordonnées x y. L'axe X du plan va de moins 5 à 5. L'axe Y du plan va de moins 4 à 4. La parabole a un sommet en (0, 0) et s'ouvre vers le haut. La droite a une pente de 2 avec une intersection y à moins 1. La parabole et la ligne ne se croisent pas, donc le système n'a pas de solution.
    Figure 11.E.29

    3.

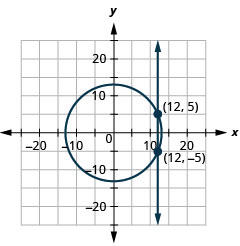
    La figure montre un cercle et une ligne tracés sur le plan de coordonnées x y. L'axe X du plan va de moins 20 à 20. L'axe Y du plan va de moins 15 à 15. Le cercle a un centre en (0, 0) et un rayon de 13. La ligne est verticale. Le cercle et la ligne se croisent aux points (12, 5) et (12, moins 5), qui sont étiquetés. La solution du système est (12, 5) et (12, négatif 5)
    Figure 11.E.30
    Exercice\(\PageIndex{20}\) Solve a System of Nonlinear Equations Using Substitution

    Dans les exercices suivants, résolvez le système d'équations en utilisant la substitution.

    1. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=-2 x+2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x-y=4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {y-x=5}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)
    Réponse

    1. \((-1,4)\)

    3. Aucune solution

    Exercice\(\PageIndex{21}\) Solve a System of Nonlinear Equations Using Elimination

    Dans les exercices suivants, résolvez le système d'équations en utilisant l'élimination.

    1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y-1=0}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}-y^{2}=5} \\ {-2 x^{2}-3 y^{2}=-30}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {3 y^{2}-4 x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=14} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
    Réponse

    1. \((-\sqrt{7}, 3),(\sqrt{7}, 3)\)

    3. \((-3,0),(0,-2),(0,2)\)

    Exercice\(\PageIndex{22}\) Use a System of Nonlinear Equations to Solve Applications

    Dans les exercices suivants, résolvez le problème à l'aide d'un système d'équations.

    1. La somme des carrés de deux nombres est\(25\). La différence entre les chiffres est\(1\). Trouve les numéros.
    2. La différence entre les carrés de deux nombres est\(45\). La différence entre le carré du premier nombre et le double du carré du deuxième nombre est\(9\). Trouve les numéros.
    3. Le périmètre d'un rectangle est de\(58\) mètres et sa superficie est de mètres\(210\) carrés. Détermine la longueur et la largeur du rectangle.
    4. Colton a acheté un four à micro-ondes plus grand pour sa cuisine. La diagonale de l'avant du micro-ondes mesure des\(34\) pouces. La façade a également une superficie de pouces\(480\) carrés. Quelles sont la longueur et la largeur du micro-ondes ?
    Réponse

    1. \(-3\)et\(-4\) ou\(4\) et\(3\)

    3. Si la longueur est\(14\) en pouces, la largeur est\(15\) en pouces. Si la longueur est\(15\) en pouces, la largeur est\(14\) en pouces.

    Test d'entraînement

    Exercice\(\PageIndex{23}\)

    Dans les exercices suivants, déterminez la distance entre les points et le milieu du segment de ligne dont les extrémités sont indiquées. Si nécessaire, arrondissez au dixième le plus proche.

    1. \((-4,-3)\)et\((-10,-11)\)
    2. \((6,8)\)et\((-5,-3)\)
    Réponse

    1. Distance :\(10,\) point médian :\((-7,-7)\)

    Exercice\(\PageIndex{24}\)

    Dans les exercices suivants, écrivez la forme standard de l'équation du cercle avec les informations données.

    1. le rayon est\(11\) et le centre est\((0,0)\)
    2. le rayon est\(12\) et le centre est\((10,-2)\)
    3. le centre est\((-2,3)\) et un point du cercle est\((2,-3)\)
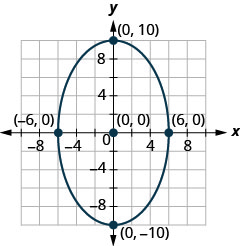
    4. Trouvez l'équation de l'ellipse illustrée sur le graphique.
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'ellipse possède un centre à (0, 0), un grand axe vertical, des sommets à (0, plus ou moins 10) et des co-sommets à (plus ou moins 6, 0).
    Figure 11.E.31
    Réponse

    1. \(x^{2}+y^{2}=121\)

    3. \((x+2)^{2}+(y-3)^{2}=52\)

    Exercice\(\PageIndex{25}\)

    Dans les exercices suivants,

    1. Identifiez le type de graphe de chaque équation sous la forme d'un cercle, d'une parabole, d'une ellipse ou d'une hyperbole, et
    2. Tracez l'équation.
    1. \(4 x^{2}+49 y^{2}=196\)
    2. \(y=3(x-2)^{2}-2\)
    3. \(3 x^{2}+3 y^{2}=27\)
    4. \(\frac{y^{2}}{100}-\frac{x^{2}}{36}=1\)
    5. \(\frac{x^{2}}{16}+\frac{y^{2}}{81}=1\)
    6. \(x=2 y^{2}+10 y+7\)
    7. \(64 x^{2}-9 y^{2}=576\)
    Réponse

    1.

    1. Ellipse
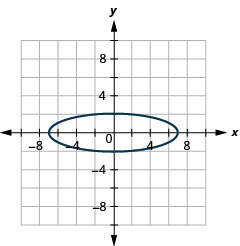
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 8 à 8. L'ellipse possède un centre à (0, 0), un axe principal horizontal, des sommets à (plus ou moins 7, 0) et des co-sommets à (0, plus ou moins 2).
    Figure 11.E.32

    3.

    1. cercle
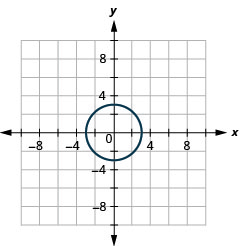
    La figure montre un cercle tracé sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 8 à 8. Le cercle parabolique a un centre en (0, 0) et un rayon de 3.
    Figure 11.E.33

    5.

    1. Ellipse
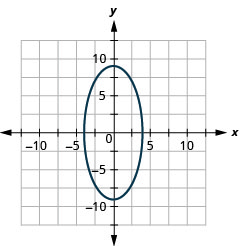
    La figure montre une ellipse tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'ellipse possède un centre à (0, 0), un grand axe vertical, des sommets à (0, plus ou moins 9) et des co-sommets à (plus ou moins 4, 0).
    Figure 11.E.34

    7.

    1. Hyperbole
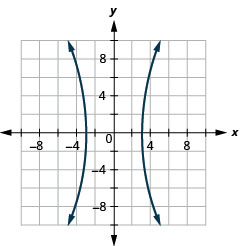
    La figure montre une hyperbole tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 8 à 8. L'hyperbole a un centre en (0, 0) et des branches qui passent par les sommets (plus ou moins 3, 0) et qui s'ouvrent à gauche et à droite.
    Figure 11.E.35
    Exercice\(\PageIndex{26}\)

    Dans les exercices suivants,

    1. Identifiez le type de graphe de chaque équation sous forme de cercle, de parabole, d'ellipse ou d'hyperbole,
    2. Écrivez l'équation sous forme standard, et
    3. Tracez l'équation.
    1. \(25 x^{2}+64 y^{2}+200 x-256 y-944=0\)
    2. \(x^{2}+y^{2}+10 x+6 y+30=0\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(9 x^{2}-25 y^{2}-36 x-50 y-214=0\)
    5. \(y=x^{2}+6 x+8\)
    6. Résolvez le système d'équations non linéaire en graphiant :\(\left\{\begin{array}{l}{3 y^{2}-x=0} \\ {y=-2 x-1}\end{array}\right.\).
    7. Résolvez le système d'équations non linéaire en utilisant la substitution :\(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {y=-x-4}\end{array}\right.\).
    8. Résolvez le système d'équations non linéaire en utilisant l'élimination :\(\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
    9. Créez l'équation de l'arc parabolique formé dans la fondation du pont illustré. Donnez la réponse sous\(y=a x^{2}+b x+c\) forme.
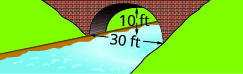
    La figure montre un arc parabolique formé dans les fondations du pont. L'arche mesure 10 pieds de haut et 30 pieds de large.
    Figure 11.E.36

    10. Une comète se déplace sur une orbite elliptique autour du soleil. La comète se rapproche le plus du soleil approximativement\(20\) au et la plus éloignée se trouve à peu près\(70\) au UA. Le soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de la comète.

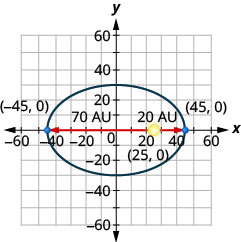
    La figure montre un modèle d'une orbite elliptique autour du soleil sur le plan de coordonnées x y. L'ellipse a un centre en (0, 0), un grand axe horizontal, des sommets marqués à (plus ou moins 45, 0), le soleil marqué comme foyer et étiqueté (25, 0), la distance la plus proche entre la comète et le soleil est marquée par 20 A U, et la plus éloignée d'une comète est marquée par 70 A U.
    Figure 11.E.37

    11. La somme de deux nombres est\(22\) et le produit est\(−240\). Trouve les numéros.

    12. Pour son anniversaire, les grands-parents d'Olive lui ont acheté un nouveau téléviseur à écran large. Avant de l'ouvrir, elle veut s'assurer qu'il s'adapte à son centre de divertissement. Le téléviseur est\(55\) ». La taille d'un téléviseur est mesurée sur la diagonale de l'écran et un écran large a une longueur supérieure à la largeur. L'écran a également une surface de pouces\(1452\) carrés. Son centre de divertissement dispose d'un insert pour le téléviseur d'une longueur de\(50\) pouces et d'une largeur de\(40\) pouces. Quelles sont la longueur et la largeur de l'écran de télévision et conviendra-t-il au centre de divertissement d'Olive ?

    Réponse

    2.

    1. cercle
    2. \((x+5)^{2}+(y+3)^{2}=4\)
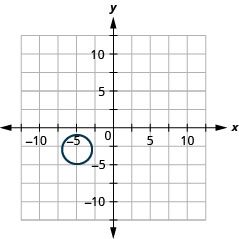
    La figure montre un cercle tracé sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. Le cercle a un centre en (moins 5, moins 3) et un rayon 2.
    Figure 11.E.38

    4.

    1. Hyperbole
    2. \(\frac{(x-2)^{2}}{25}-\frac{(y+1)^{2}}{9}=1\)
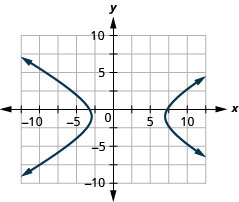
    La figure montre une hyperbole tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 14 à 14. L'axe Y du plan va de moins 10 à 10. L'hyperbole a un centre en (2, moins 1) et des branches qui passent par les sommets (négatif 3, négatif 1) et (7, négatif 1) qui s'ouvrent à gauche et à droite.
    Figure 11.E.39

    6. Aucune solution

    8. \((0,-3),(0,3)\)

    10. \(\frac{x^{2}}{2025}+\frac{y^{2}}{1400}=1\)

    12. La longueur est\(44\) en pouces et la largeur en\(33\) pouces. Le téléviseur s'adaptera au centre de divertissement d'Olive.

    Lexique

    système d'équations non linéaires
    Un système d'équations non linéaires est un système dans lequel au moins l'une des équations n'est pas linéaire.