11.6 : Résolution de systèmes d'équations non linéaires

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Résolvez un système d'équations non linéaires à l'aide de graphiques
• Résolvez un système d'équations non linéaires par substitution
• Résolvez un système d'équations non linéaires par élimination
• Utiliser un système d'équations non linéaires pour résoudre des applications

Avant de commencer, répondez à ce questionnaire de préparation.

1. Résolvez le système en représentant graphiquement :$\left\{\begin{array}{l}{x-3 y=-3} \\ {x+y=5}\end{array}\right.$.
   Si vous avez oublié ce problème, consultez l'exemple 4.2.
2. Résolvez le système par substitution :$\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.$
   si vous avez oublié ce problème, consultez l'exemple 4.7.
3. Résolvez le système par élimination :$\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.$
   si vous avez oublié ce problème, consultez l'exemple 4.9.

Résolvez un système d'équations non linéaires à l'aide de graphiques

Nous avons appris à résoudre des systèmes d'équations linéaires à deux variables par représentation graphique, substitution et élimination. Nous utiliserons ces mêmes méthodes lorsque nous examinerons des systèmes d'équations non linéaires comportant deux équations et deux variables. Un système d'équations non linéaires est un système dans lequel au moins l'une des équations n'est pas linéaire.

Par exemple, chacun des systèmes suivants est un système d'équations non linéaires.

$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right. \left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right. \left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$

Définition$\PageIndex{1}$

Un système d'équations non linéaires est un système dans lequel au moins l'une des équations n'est pas linéaire.

Tout comme pour les systèmes d'équations linéaires, la solution d'un système non linéaire est une paire ordonnée qui rend les deux équations vraies. Dans un système non linéaire, il peut y avoir plusieurs solutions. Nous allons le voir en résolvant un système d'équations non linéaires par représentation graphique.

Lorsque nous avons résolu des systèmes d'équations linéaires, la solution du système était le point d'intersection des deux droites. Avec les systèmes d'équations non linéaires, les graphes peuvent être des cercles, des paraboles ou des hyperboles et il peut y avoir plusieurs points d'intersection, et donc plusieurs solutions. Une fois que vous avez identifié les graphes, visualisez les différentes manières dont les graphes peuvent se croiser et ainsi le nombre de solutions possibles.

Pour résoudre des systèmes d'équations non linéaires à l'aide de graphes, nous utilisons essentiellement les mêmes étapes que pour les systèmes d'équations linéaires légèrement modifiés pour les équations non linéaires. Les étapes sont répertoriées ci-dessous à titre de référence.

Résolvez un système d'équations non linéaires en traçant un graphique.

1. Identifiez le graphique de chaque équation. Esquissez les options d'intersection possibles.
2. Tracez la première équation.
3. Tracez la deuxième équation sur le même système de coordonnées rectangulaires.
4. Déterminez si les graphes se croisent.
5. Identifiez les points d'intersection.
6. Vérifiez que chaque paire ordonnée est une solution aux deux équations d'origine.

Exemple$\PageIndex{1}$

Résolvez le système en représentant graphiquement :$\left\{\begin{array}{l}{x-y=-2} \\ {y=x^{2}}\end{array}\right.$

Solution :

Tableau 11.5.1

Identifiez chaque graphique.	$\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.$
Esquissez les options possibles pour l'intersection d'une parabole et d'une droite.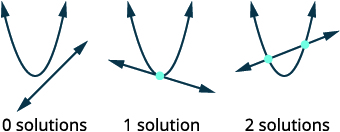
Tracez la ligne,$x-y=-2$. Forme d'interception en pente$y=x+2$. Tracez la parabole,$y=x^{2}$.
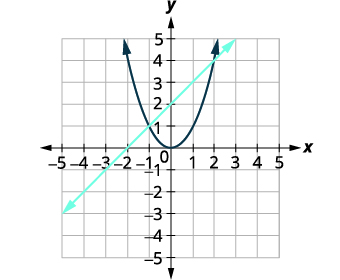Identifiez les points d'intersection.	Les points d'intersection semblent être$(2,3)$ et$(-1,1)$.
Assurez-vous que chaque solution répond aux deux équations. $(2,4)$ $\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}$ $(-1,1)$ $\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}$
	Les solutions sont$(2,4)$ et$(-1,1)$.

Exercice$\PageIndex{1}$

Résolvez le système en représentant graphiquement :$\left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$.

Réponse

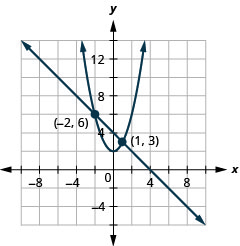
Graphique 11.5.3

Exercice$\PageIndex{2}$

Résolvez le système en représentant graphiquement :$\left\{\begin{array}{l}{x-y=-1} \\ {y=-x^{2}+3}\end{array}\right.$

Réponse

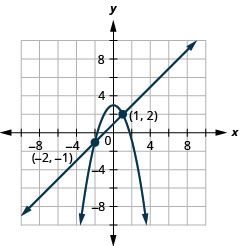
Graphique 11.5.4

Pour identifier le graphe de chaque équation, gardez à l'esprit les caractéristiques des$y^{2}$ termes$x^{2}$ et de chaque conique.

Exemple$\PageIndex{2}$

Résolvez le système en représentant graphiquement :$\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$.

Solution :

Tableau 11.5.2

Identifiez chaque graphique.	$\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.$
Esquissez les options possibles pour l'intersection d'un cercle et d'une ligne.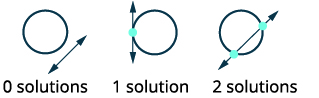
Tracez le cercle,$(x-2)^{2}+(y+3)^{2}=4$ Centre :$(2,-3)$ rayon :$2$ Tracez la ligne,$y=-1$. Il s'agit d'une ligne horizontale.
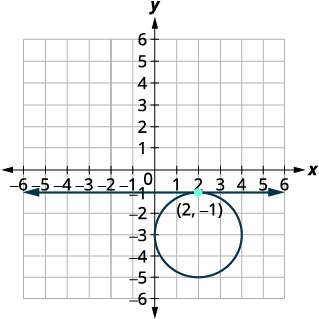Identifiez les points d'intersection.	Le point d'intersection semble être$(2,-1)$.
Assurez-vous que la solution répond aux deux équations. $(2,-1)$ $\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}$
	La solution est$(2,-1)$

Exercice$\PageIndex{3}$

Résolvez le système en représentant graphiquement :$\left\{\begin{array}{l}{x=-6} \\ {(x+3)^{2}+(y-1)^{2}=9}\end{array}\right.$

Réponse

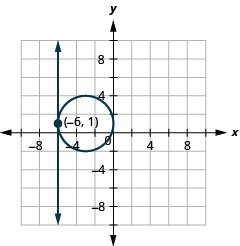
Graphique 11.5.7

Exercice$\PageIndex{4}$

Résolvez le système en représentant graphiquement :$\left\{\begin{array}{l}{y=4} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$

Réponse

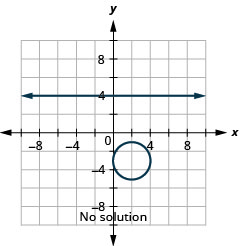
Graphique 11.5.8

Résoudre un système d'équations non linéaires par substitution

La méthode graphique fonctionne bien lorsque les points d'intersection sont des nombres entiers et sont donc faciles à lire sur le graphique. Mais le plus souvent, il est difficile de lire les coordonnées des points d'intersection. La méthode de substitution est une méthode algébrique qui fonctionne bien dans de nombreuses situations. Cela fonctionne particulièrement bien lorsqu'il est facile de résoudre l'une des équations pour l'une des variables.

La méthode de substitution est très similaire à la méthode de substitution que nous avons utilisée pour les systèmes d'équations linéaires. Les étapes sont répertoriées ci-dessous à titre de référence.

Résoudre un système d'équations non linéaires par substitution

1. Identifiez le graphique de chaque équation. Esquissez les options d'intersection possibles.
2. Résolvez l'une des équations pour l'une des variables.
3. Remplacez l'expression de l'étape 2 dans l'autre équation.
4. Résolvez l'équation résultante.
5. Remplacez chaque solution de l'étape 4 dans l'une des équations d'origine pour trouver l'autre variable.
6. Écrivez chaque solution sous la forme d'une paire ordonnée.
7. Vérifiez que chaque paire ordonnée est une solution aux deux équations d'origine.

Exemple$\PageIndex{3}$

Résolvez le système en utilisant la substitution :$\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right.$

Solution :

Tableau 11.5.3

Identifiez chaque graphique.	$\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.$
Esquissez les options possibles pour l'intersection d'une ellipse et d'une ligne.
L'équation$y=3x-3$ est résolue pour$y$.
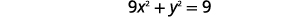Remplacez$3x-3$$y$ par dans la première équation.
Résolvez l'équation pour$x$.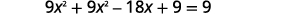
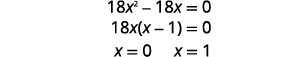$x=0$Substituez et$x=1$ entrez$y=3x-3$ pour trouver$y$ -.
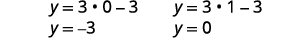	Les paires commandées sont$(0,-3), (1,0)$.
Vérifiez les deux paires ordonnées dans les deux équations. $(0,-3)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}$ $(1,0)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}$
	Les solutions sont$(0,-3), (1,0)$.

Exercice$\PageIndex{5}$

Résolvez le système en utilisant la substitution :$\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {y=\frac{1}{3} x-3}\end{array}\right.$

Réponse

Aucune solution

Exercice$\PageIndex{6}$

Résolvez le système en utilisant la substitution :$\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=x+2}\end{array}\right.$

Réponse

$\left(-\frac{4}{5}, \frac{6}{5}\right),(0,2)$

Jusqu'à présent, chaque système d'équations non linéaires a eu au moins une solution. L'exemple suivant montrera une autre option.

Exemple$\PageIndex{4}$

Résolvez le système en utilisant la substitution :$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=x-2}\end{array}\right.$

Solution :

Tableau 11.5.4

Identifiez chaque graphique.	$\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.$
Esquissez les options possibles pour l'intersection d'une parabole et d'une droite.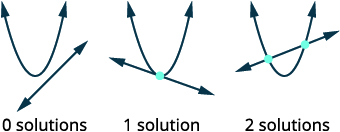
L'équation$y=x-2$ est résolue pour$y$.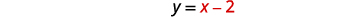
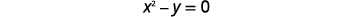Remplacez$x-2$$y$ par dans la première équation.
Résolvez l'équation pour$x$.
Cela ne prend pas facilement en compte, nous pouvons donc vérifier le discriminant.
$\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}$	Le discriminant est négatif, il n'y a donc pas de véritable solution. Le système n'a pas de solution.

Exercice$\PageIndex{7}$

Résolvez le système en utilisant la substitution :$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=2 x-3}\end{array}\right.$

Réponse

Aucune solution

Exercice$\PageIndex{8}$

Résolvez le système en utilisant la substitution :$\left\{\begin{array}{l}{y^{2}-x=0} \\ {y=3 x-2}\end{array}\right.$

Réponse

$\left(\frac{4}{9},-\frac{2}{3}\right),(1,1)$

Résoudre un système d'équations non linéaires par élimination

Lorsque nous avons étudié des systèmes d'équations linéaires, nous avons utilisé la méthode d'élimination pour résoudre le système. Nous pouvons également utiliser l'élimination pour résoudre des systèmes d'équations non linéaires. Cela fonctionne bien lorsque les deux variables sont mises au carré dans les équations. Lorsque nous utilisons l'élimination, nous essayons de faire en sorte que les coefficients d'une variable soient opposés. Ainsi, lorsque nous additionnons les équations, cette variable est éliminée.

La méthode d'élimination est très similaire à la méthode d'élimination que nous avons utilisée pour les systèmes d'équations linéaires. Les étapes sont répertoriées à titre de référence.

Résoudre un système d'équations par élimination

1. Identifiez le graphique de chaque équation. Esquissez les options d'intersection possibles.
2. Écrivez les deux équations sous forme standard.
3. Faites en sorte que les coefficients d'une variable soient opposés.
   Déterminez quelle variable vous allez éliminer.
   Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés.
4. Ajoutez les équations résultant de l'étape 3 pour éliminer une variable.
5. Résolvez pour la variable restante.
6. Remplacez chaque solution de l'étape 5 par l'une des équations d'origine. Résolvez ensuite pour l'autre variable.
7. Écrivez chaque solution sous la forme d'une paire ordonnée.
8. Vérifiez que chaque paire ordonnée est une solution aux deux équations d'origine.

Exemple$\PageIndex{5}$

Résolvez le système par élimination :$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=4}\end{array}\right.$

Solution :

Tableau 11.5.5

Identifiez chaque graphique.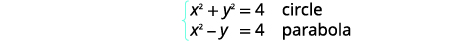
Esquissez les options possibles pour l'intersection d'un cercle et d'une parabole.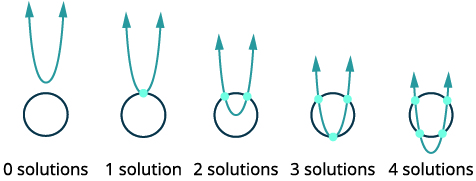
Les deux équations sont présentées sous forme standard.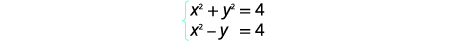
Pour obtenir les coefficients opposés de$x^{2}$, nous allons multiplier la deuxième équation par$-1$.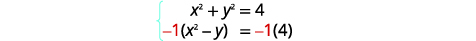
Simplifiez.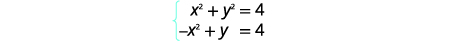
Ajoutez les deux équations pour éliminer$x^{2}$/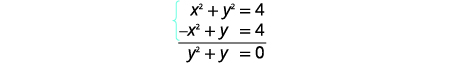
Résolvez pour$y$.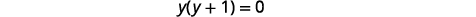
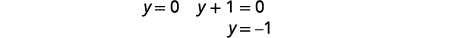Remplacez$y=0$ et$y=-1$ dans l'une des équations originales. Alors résolvez pour$x$.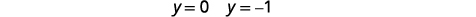
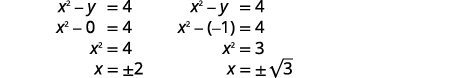Écrivez chaque solution sous la forme d'une paire ordonnée.	Les paires commandées sont$(-2,0)(2,0)$. $(\sqrt{3},-1)(-\sqrt{3},-1)$
Vérifiez que chaque paire ordonnée est une solution aux deux équations d'origine.
Nous vous laisserons le soin de vérifier chacune des quatre solutions.	Les solutions sont$(-2,0),(2,0),(\sqrt{3},-1)$, et$(-\sqrt{3},-1)$.

Exercice$\PageIndex{9}$

Résolvez le système par élimination :$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right.$

Réponse

$(-3,0),(3,0),(-2 \sqrt{2},-1),(2 \sqrt{2},-1)$

Exercice$\PageIndex{10}$

Résolvez le système par élimination :$\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {-x+y^{2}=1}\end{array}\right.$

Réponse

$(-1,0),(0,1),(0,-1)$

Il existe également quatre options lorsque l'on considère un cercle et une hyperbole.

Exemple$\PageIndex{6}$

Résolvez le système par élimination :$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$

Solution :

Tableau 11.5.6

Identifiez chaque graphique.	$\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.$
Esquissez les options possibles pour l'intersection d'un cercle et d'une hyperbole.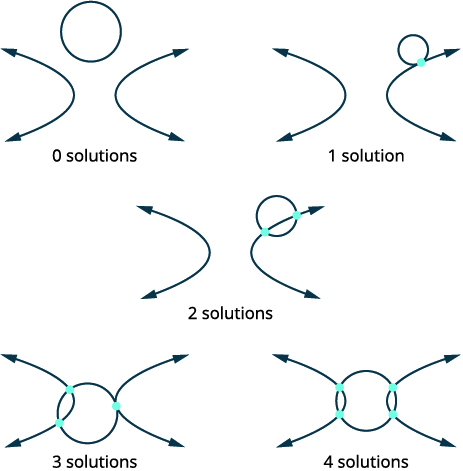
Les deux équations sont présentées sous forme standard.	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$
Les coefficients de$y^{2}$ sont opposés, nous allons donc ajouter les équations.	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$ $2 x^{2}=8$
Simplifiez.	$x^{2}=4$ $x=\pm 2$ $x=2 \quad x=-2$
Remplacez$x=2$ et$x=-2$ dans l'une des équations originales. Alors résolvez pour$y$.	$\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}$
Écrivez chaque solution sous la forme d'une paire ordonnée.	Les paires ordonnées sont$(-2, \sqrt{3}),(-2,-\sqrt{3})$,$(2, \sqrt{3}),$ et$(2,-\sqrt{3})$.
Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.
Nous vous laisserons le soin de vérifier chacune des quatre solutions.	Les solutions sont$(-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})$, et$(2,-\sqrt{3})$.

Exercice$\PageIndex{11}$

Résolvez le système par élimination :$\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y^{2}-x^{2}=7}\end{array}\right.$

Réponse

$(-3,-4),(-3,4),(3,-4),(3,4)$

Exercice$\PageIndex{12}$

Résolvez le système par élimination :$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y^{2}=4}\end{array}\right.$

Réponse

$(-2,0),(2,0)$

Utiliser un système d'équations non linéaires pour résoudre des applications

Les systèmes d'équations non linéaires peuvent être utilisés pour modéliser et résoudre de nombreuses applications. Nous allons prendre comme exemple une situation géométrique quotidienne.

Exemple$\PageIndex{7}$

La différence entre les carrés de deux nombres est$15$. La somme des nombres est$5$. Trouve les numéros.

Solution :

Tableau 11.5.7

Identifiez ce que nous recherchons.	Deux numéros différents.
Définissez les variables.	$x$=premier chiffre $y$=deuxième numéro
Traduisez les informations en un système d'équations.
Première phrase.	La différence entre les carrés de deux nombres est$15$.
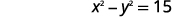Deuxième phrase.	La somme des nombres est$5$.
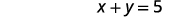Résolvez le système par substitution.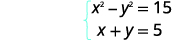
Résolvez la deuxième équation pour$x$.
Substituer$x$ dans la première équation.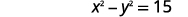
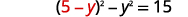Développez et simplifiez.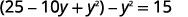
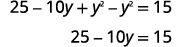Résolvez pour$y$.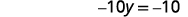
Remettre dans la deuxième équation.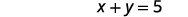
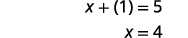	Les chiffres sont$1$ et$4$.

Exercice$\PageIndex{13}$

La différence entre les carrés de deux nombres est$−20$. La somme des nombres est$10$. Trouve les numéros.

Réponse

$4$et$6$

Exercice$\PageIndex{14}$

La différence entre les carrés de deux nombres est$35$. La somme des nombres est$−1$. Trouve les numéros.

Réponse

$-18$et$17$

Exemple$\PageIndex{8}$

Myra a acheté un$25$ « petit » téléviseur pour sa cuisine. La taille d'un téléviseur est mesurée sur la diagonale de l'écran. L'écran a également une surface de pouces$300$ carrés. Quelles sont la longueur et la largeur de l'écran du téléviseur ?

Solution :

Tableau 11.5.8

Identifiez ce que nous recherchons.	La longueur et la largeur du rectangle.
Définissez les variables.	Soit$x$ la largeur du rectangle $y$= longueur du rectangle
Dessinez un diagramme pour vous aider à visualiser la situation.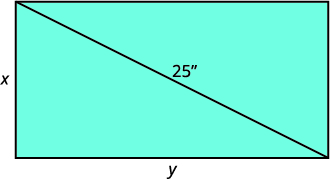
	La superficie est en pouces$300$ carrés.
Traduisez les informations en un système d'équations.	La diagonale du triangle droit est$25$ en pouces.
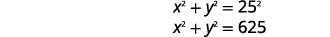	La surface du rectangle est en pouces$300$ carrés.
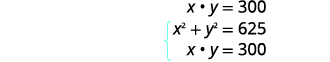Résolvez le système en utilisant la substitution.
Résolvez la deuxième équation pour$x$.
Substituer$x$ dans la première équation.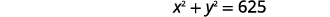
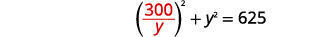Simplifiez.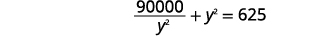
Multipliez par$y^{2}$ pour effacer les fractions.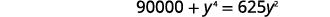
Mettre sous forme standard.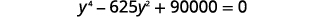
Résolvez par factorisation.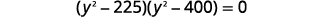
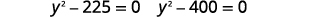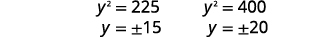Comme$y$ c'est un côté du rectangle, nous supprimons les valeurs négatives.
Remettre dans la deuxième équation.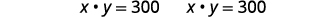
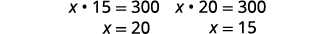	Si la longueur est$15$ en pouces, la largeur est$20$ en pouces.
	Si la longueur est$20$ en pouces, la largeur est$15$ en pouces.

Exercice$\PageIndex{15}$

Edgar a acheté une$20$ « petite » télévision pour son garage. La taille d'un téléviseur est mesurée sur la diagonale de l'écran. L'écran a également une surface de pouces$192$ carrés. Quelles sont la longueur et la largeur de l'écran du téléviseur ?

Réponse

Si la longueur est$12$ en pouces, la largeur est$16$ en pouces. Si la longueur est$16$ en pouces, la largeur est$12$ en pouces.

Exercice$\PageIndex{16}$

La famille Harper a acheté un petit four à micro-ondes pour sa chambre familiale. La diagonale de la porte mesure$15$ en pouces. La porte a également une superficie de pouces$108$ carrés. Quelles sont la longueur et la largeur de la porte du four à micro-ondes ?

Réponse

Si la longueur est$12$ en pouces, la largeur est$9$ en pouces. Si la longueur est$9$ en pouces, la largeur est$12$ en pouces.

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre des équations non linéaires.

• Systèmes d'équations non linéaires
• Résolvez un système d'équations non linéaires
• Résoudre un système d'équations non linéaires par élimination
• Système d'équations non linéaires — Application à une zone et à un périmètre

Concepts clés

• Comment résoudre un système d'équations non linéaires par représentation graphique.
  1. Identifiez le graphique de chaque équation. Esquissez les options d'intersection possibles.
  2. Tracez la première équation.
  3. Tracez la deuxième équation sur le même système de coordonnées rectangulaires.
  4. Déterminez si les graphes se croisent.
  5. Identifiez les points d'intersection.
  6. Vérifiez que chaque paire ordonnée est une solution aux deux équations d'origine.
• Comment résoudre un système d'équations non linéaires par substitution.
  1. Identifiez le graphique de chaque équation. Esquissez les options d'intersection possibles.
  2. Résolvez l'une des équations pour l'une des variables.
  3. Remplacez l'expression de l'étape 2 dans l'autre équation.
  4. Résolvez l'équation résultante.
  5. Remplacez chaque solution de l'étape 4 dans l'une des équations d'origine pour trouver l'autre variable.
  6. Écrivez chaque solution sous la forme d'une paire ordonnée.
  7. Vérifiez que chaque paire ordonnée est une solution aux deux équations d'origine.
• Comment résoudre un système d'équations par élimination.
  1. Identifiez le graphique de chaque équation. Esquissez les options d'intersection possibles.
  2. Écrivez les deux équations sous forme standard.
  3. Faites en sorte que les coefficients d'une variable soient opposés.
     Déterminez quelle variable vous allez éliminer.
     Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés.
  4. Ajoutez les équations résultant de l'étape 3 pour éliminer une variable.
  5. Résolvez pour la variable restante.
  6. Remplacez chaque solution de l'étape 5 par l'une des équations d'origine. Résolvez ensuite pour l'autre variable.
  7. Écrivez chaque solution sous la forme d'une paire ordonnée.
  8. Vérifiez que chaque paire ordonnée est une solution aux deux équations d'origine.