Home
Français
Algèbre intermédiaire (OpenStax)
9 : Équations et fonctions quadratiques
9.8 : Représenter graphiquement des fonctions quadratiques à l'aide

9.8 : Représenter graphiquement des fonctions quadratiques à l'aide

Last updated
Save as PDF

Page ID: 194345

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Représenter graphiquement les fonctions quadratiques du formulaire$f(x)=x^{2}+k$
Représenter graphiquement les fonctions quadratiques du formulaire$f(x)=(x−h)^{2}$
Représenter graphiquement les fonctions quadratiques du formulaire$f(x)=ax^{2}$
Représenter graphiquement des fonctions quadratiques en utilisant
Trouvez une fonction quadratique à partir de son graphique

Avant de commencer, répondez à ce questionnaire de préparation.

Représentez graphiquement la fonction$f(x)=x^{2}$ en traçant des points.
Si vous avez oublié ce problème, consultez l'exemple 3.54.
Facteur complètement :$y^{2}−14y+49$.
Si vous avez oublié ce problème, consultez l'exemple 6.24.
Facteur complètement :$2x^{2}−16x+32$.
Si vous avez oublié ce problème, consultez l'exemple 6.26.

Représenter graphiquement les fonctions quadratiques du formulaire$f(x)=x^{2}+k$

Dans la dernière section, nous avons appris à représenter graphiquement des fonctions quadratiques à l'aide de leurs propriétés. Une autre méthode consiste à commencer par le graphe de base$f(x)=x^{2}$ et à le « déplacer » en fonction des informations données dans l'équation de la fonction. C'est ce que nous appelons la représentation graphique de fonctions quadratiques utilisant des transformations.

Dans le premier exemple, nous allons représenter graphiquement la fonction quadratique$f(x)=x^{2}$ en traçant des points. Ensuite, nous verrons quel effet l'ajout d'une constante$k$, à l'équation aura sur le graphique de la nouvelle fonction$f(x)=x^{2}+k$.

Exemple$\PageIndex{1}$

Graphe$f(x)=x^{2}$$g(x)=x^{2}+2$, et$h(x)=x^{2}−2$ sur le même système de coordonnées rectangulaires. Décrivez l'effet de l'ajout d'une constante à la fonction sur la parabole de base.

Solution :

Le fait de tracer des points nous aidera à voir l'effet des constantes sur le$f(x)=x^{2}$ graphique de base. Nous remplissons le tableau pour les trois fonctions.

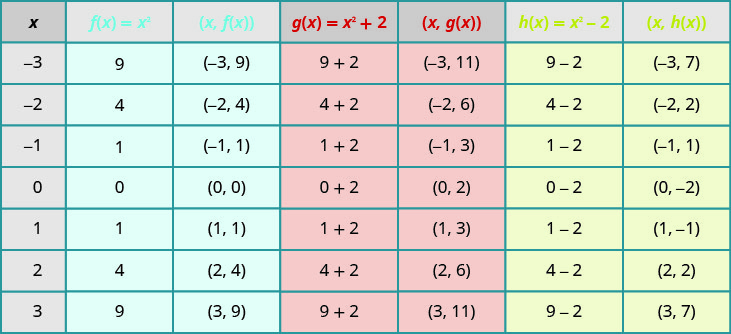
Tableau illustrant l'effet des constantes sur la fonction de base de x au carré. Le tableau comporte sept colonnes intitulées x, f de x est égal à x au carré, la paire ordonnée (x, f de x), g de x est égal à x au carré plus 2, la paire ordonnée (x, g de x), h de x est égal à x au carré moins 2 et la paire ordonnée (x, h de x). Dans la colonne x, les valeurs indiquées sont négatives 3, négatives 2, négatives 1, 0, 1, 2 et 3. Dans la colonne f de x égale x au carré, les valeurs sont 9, 4, 1, 0, 1, 4 et 9. Dans la colonne (x, f ou x), les paires ordonnées (négatif 3, 9), (négatif 2, 4), (négatif 1, 1), (0, 0), (1, 1), (2, 4) et (3, 9) sont données. La colonne g de x égale x au carré plus 2 contient les expressions 9 plus 2, 4 plus 2, 1 plus 2, 0 plus 2, 1 plus 2, 1 plus 2, 4 plus 2 et 9 plus 2. La colonne (x, g ou x) contient les paires ordonnées de (négatif 3, 11), (négatif 2, 6), (négatif 1, 3), (0, 2), (1, 3), (2, 6) et (3, 11). Dans la colonne h où x est égal à x au carré moins 2, les expressions données sont 9 moins 2, 4 moins 2, 1 moins 2, 0 moins 2, 1 moins 2, 1 moins 2, 4 moins 2 et 9 moins 2. Dans la dernière colonne, (x, h ou x), contient les paires ordonnées (négatif 3, 7), (négatif 2, 2), (négatif 1, négatif 1), (0, négatif 2), (1, négatif 1), (2, 2) et (3, 7). — Graphique 9.7.1

Les$g(x)$ valeurs sont deux de plus que les$f(x)$ valeurs. De plus, les$h(x)$ valeurs sont inférieures de deux aux$f(x)$ valeurs. Nous allons maintenant représenter graphiquement les trois fonctions sur le même système de coordonnées rectangulaires.

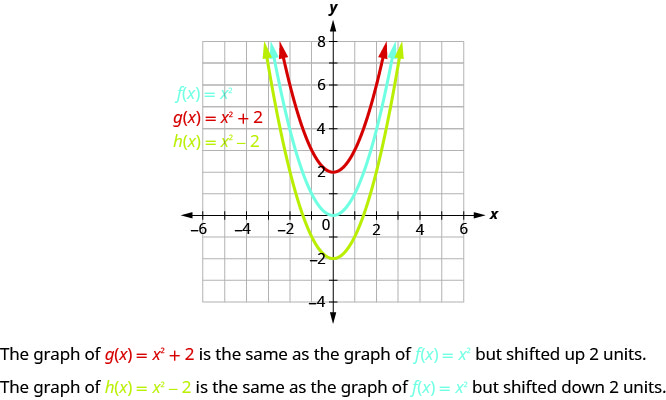
Cette figure montre 3 paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. Le milieu est le graphe de f si x est égal à x, au carré, a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La parabole supérieure a été déplacée de 2 unités vers le haut et de 2 unités vers le bas. — Graphique 9.7.2

Le graphique de$g(x)=x^{2}+2$ est identique à celui des$2$ unités,$f(x)=x^{2}$ mais décalé vers le haut.

Le graphique de$h(x)=x^{2}−2$ est identique à celui des$2$ unités,$f(x)=x^{2}$ mais décalé vers le bas.

Exercice$\PageIndex{1}$

Graphe$f(x)=x^{2}, g(x)=x^{2}+1,$ et$h(x)=x^{2}-1$ sur le même système de coordonnées rectangulaires.
Décrivez l'effet de l'ajout d'une constante à la fonction sur la parabole de base.

Réponse

un.

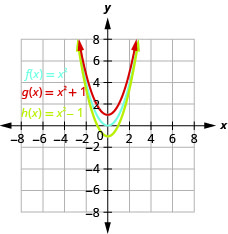
Cette figure montre 3 paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. Le graphique du milieu est de f si x est égal à x, au carré, a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe supérieure a été déplacée d'une unité vers le haut et d'une unité vers le bas. — Graphique 9.7.3

b. Le graphique de$g(x)=x^{2}+1$ est identique à celui de l'$1$unité$f(x)=x^{2}$ mais décalée vers le haut. Le graphique de$h(x)=x^{2}−1$ est identique à celui de l'$1$unité$f(x)=x^{2}$, mais décalé vers le bas.

Exercice$\PageIndex{2}$

Graphe$f(x)=x^{2}, g(x)=x^{2}+6,$ et$h(x)=x^{2}-6$ sur le même système de coordonnées rectangulaires.
Décrivez l'effet de l'ajout d'une constante à la fonction sur la parabole de base.

Réponse

un.

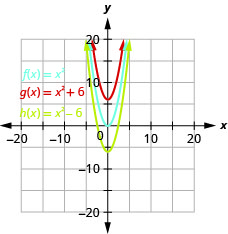
Cette figure montre 3 paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. La courbe du milieu est le graphique de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe supérieure a été déplacée de 6 unités vers le haut et de 6 unités vers le bas. — Graphique 9.7.4

b. Le graphique de$h(x)=x^{2}+6$ est identique à celui des$6$ unités,$f(x)=x^{2}$ mais décalé vers le haut. Le graphique de$h(x)=x^{2}-6$ est identique à celui des$6$ unités,$f(x)=x^{2}$ mais décalé vers le bas.

Le dernier exemple nous montre que pour représenter graphiquement une fonction quadratique de la forme$f(x)=x^{2}+k$, nous prenons le graphe parabolique de base de$f(x)=x^{2}$ et le décalons verticalement vers le haut$(k>0)$ ou vers le bas$(k<0)$.

Cette transformation s'appelle un décalage vertical.

Tracez une fonction quadratique du formulaire à$f(x)=x^{2}+k$ l'aide d'un décalage vertical

Le graphe de$f(x)=x^{2}+k$ déplace le graphe des$k$ unités$f(x)=x^{2}$ verticales.

Si$k>0$, déplacez la parabole verticalement vers le haut$k$ d'unités.
Si$k<0$, déplacez la parabole verticalement vers le bas en$|k|$ unités.

Maintenant que nous avons vu l'effet de la constante$k$, il est facile de représenter graphiquement les fonctions du formulaire$f(x)=x^{2}+k$. Nous commençons simplement par la parabole de base de,$f(x)=x^{2}$ puis nous la décalons vers le haut ou vers le bas.

Il peut être utile de s'entraîner$f(x)=x^{2}$ rapidement à dessiner. Nous connaissons les valeurs et pouvons esquisser le graphique à partir de là.

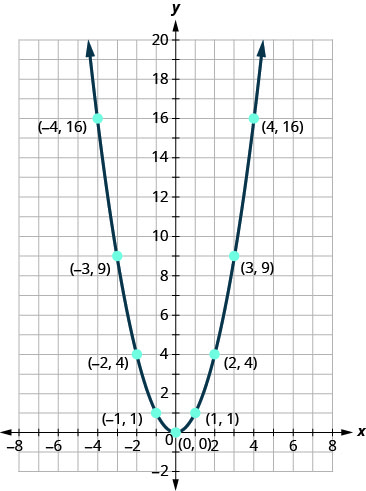
Cette figure montre une parabole s'ouvrant vers le haut sur le plan de coordonnées x y, avec un sommet (0, 0). Les autres points de la courbe sont situés à (négatif 4, 16), (négatif 3, 9), (négatif 2, 4), (négatif 1, 1), (1, 1), (2, 4), (3, 9) et (4, 16). — Graphique 9.7.5

Une fois que nous connaîtrons cette parabole, il sera facile d'appliquer les transformations. L'exemple suivant nécessitera un décalage vertical.

Exemple$\PageIndex{2}$

$f(x)=x^{2}−3$Tracez en utilisant un décalage vertical.

Solution :

Tableau 9.7.1
Nous dessinons d'abord le graphique de$f(x)=x^{2}$ sur la grille.	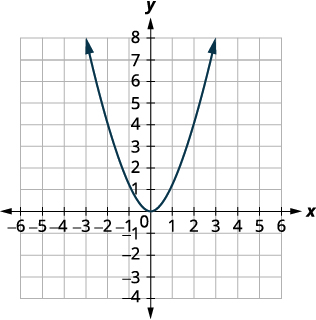$Cette figure montre une parabole s'ouvrant vers le haut sur le plan de coordonnées x y avec un sommet de (0, 0) avec les autres points de la courbe situés à (moins 1, 1) et (1, 1). C'est le graphe de f si x est égal à x au carré.$
Déterminez$k$.	$.$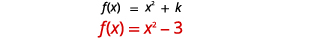
	$.$
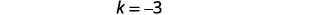Déplace le graphique$f(x)=x^{2}$ vers le bas$3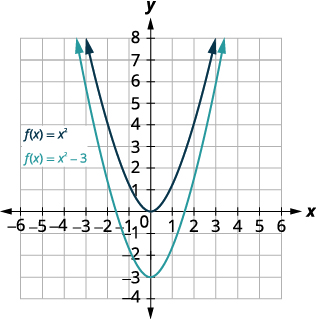$.	$Cette figure montre deux paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. La courbe supérieure est le graphique de f si x est égal à x au carré dont le sommet est (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe inférieure a été déplacée de 3 unités vers le bas.$

Exercice$\PageIndex{3}$

$f(x)=x^{2}−5$Tracez en utilisant un décalage vertical.

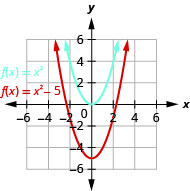
Réponse: $Cette figure montre deux paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. La courbe supérieure est le graphique de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe inférieure a été déplacée de 5 unités vers le bas.$
Graphique 9.7.10

Exercice$\PageIndex{4}$

$f(x)=x^{2}+7$Tracez en utilisant un décalage vertical.

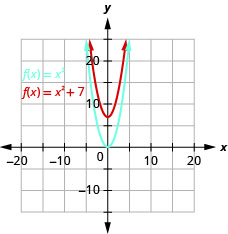
Réponse: $Cette figure montre deux paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. La courbe du bas est le graphique de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe supérieure a été remontée de 7 unités.$
Graphique 9.7.11

Représenter graphiquement les fonctions quadratiques du formulaire$f(x)=(x-h)^{2}$

Dans le premier exemple, nous avons représenté graphiquement la fonction quadratique$f(x)=x^{2}$ en traçant des points, puis nous avons vu l'effet de l'ajout d'une constante$k$ à la fonction sur le graphe résultant de la nouvelle fonction$f(x)=x^{2}+k$.

Nous allons maintenant explorer l'effet de la soustraction d'une constante,$h$, de$x$ has sur le graphe résultant de la nouvelle fonction$f(x)=(x−h)^{2}$.

Exemple$\PageIndex{3}$

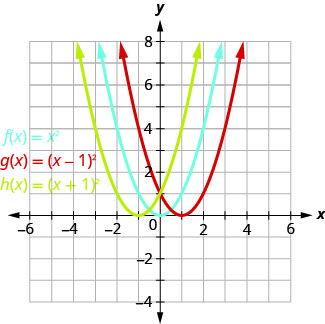
Graphe$f(x)=x^{2}, g(x)=(x-1)^{2},$ et$h(x)=(x+1)^{2}$ sur le même système de coordonnées rectangulaires. Décrivez l'effet de l'ajout d'une constante à la fonction sur la parabole de base.

Solution :

Le fait de tracer des points nous aidera à voir l'effet des constantes sur le$f(x)=x^{2}$ graphique de base. Nous remplissons le tableau pour les trois fonctions.

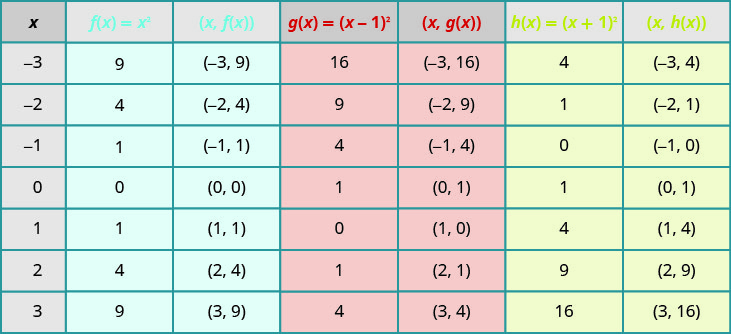
Les$g(x)$ valeurs et les$h(x)$ valeurs partagent les mêmes nombres$0, 1, 4, 9$, et$16$, mais elles sont décalées.

La figure indique sur la première ligne que le graphique de g de x est égal à la quantité x moins 1 carré est identique au graphique de f de x égal à x au carré mais décalé vers la droite d'une unité. La deuxième ligne indique que le graphique de h de x est égal à la quantité x plus 1 au carré est le même que le graphique de f si x est égal à x au carré mais décalé vers la gauche d'une unité. La troisième ligne de la figure indique que g de x est égal à la quantité x moins 1 au carré avec une flèche en dessous pointant vers la droite avec 1 unité écrite à côté. Enfin, il donne h de x égal à la quantité de x plus 1 au carré avec une flèche en dessous pointant vers la gauche avec 1 unité écrite à côté. — Graphique 9.7.14

Exercice$\PageIndex{5}$

Graphe$f(x)=x^{2}, g(x)=(x+2)^{2},$ et$h(x)=(x-2)^{2}$ sur le même système de coordonnées rectangulaires.
Décrivez l'effet de l'ajout d'une constante à la fonction sur la parabole de base.

Réponse

un.

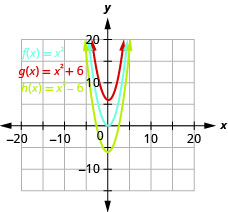
b. Le graphique de$g(x)=(x+2)^{2}$ est identique à celui des$2$ unités vers la gauche$f(x)=x^{2}$, mais décalées. Le graphique de$h(x)=(x−2)^{2}$ est identique à celui des$2$ unités,$f(x)=x^{2}$ mais décalé vers la droite.

Exercice$\PageIndex{6}$

Graphe$f(x)=x^{2}, g(x)=x^{2}+5,$ et$h(x)=x^{2}-5$ sur le même système de coordonnées rectangulaires.
Décrivez l'effet de l'ajout d'une constante à la fonction sur la parabole de base.

Réponse

un.

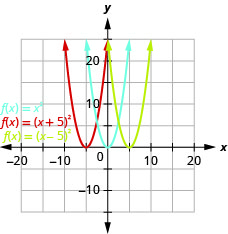
b. Le graphique de$g(x)=(x+5)^{2}$ est identique à celui des$5$ unités vers la gauche$f(x)=x^{2}$, mais décalées. Le graphique de$h(x)=(x-5)^{2}$ est identique à celui des$5$ unités droites$f(x)=x^{2}$, mais décalées.

Le dernier exemple nous montre que pour représenter graphiquement une fonction quadratique de la forme$f(x)=(x−h)^{2}$, nous prenons le graphe parabolique de base de$f(x)=x^{2}$ et nous le décalons vers la gauche$(h>0)$ ou vers la droite$(h<0)$.

Cette transformation s'appelle un décalage horizontal.

Tracez une fonction quadratique du formulaire à$f(x)=(x-h)^{2}$ l'aide d'un décalage horizontal

Le graphe de$f(x)=(x-h)^{2}$ déplace le graphe des$h$ unités$f(x)=x^{2}$ horizontales.

Si$h>0$, déplacez la parabole horizontalement vers la gauche en$h$ unités.
Si$h<0$, décalez la parabole horizontalement en$|h|$ unités droites.

Maintenant que nous avons vu l'effet de la constante$h$, il est facile de représenter graphiquement les fonctions du formulaire$f(x)=(x−h)^{2}$. Nous commençons simplement par la parabole de base de,$f(x)=x^{2}$ puis nous la décalons vers la gauche ou la droite.

L'exemple suivant nécessitera un décalage horizontal.

Exemple$\PageIndex{4}$

$f(x)=(x−6)^{2}$Tracez en utilisant un décalage horizontal.

Solution :

Tableau 9.7.2
Nous dessinons d'abord le graphique de$f(x)=x^{2}$ sur la grille.	$.$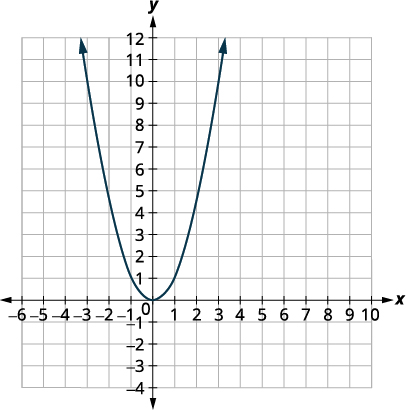
Déterminez$h$.	$.$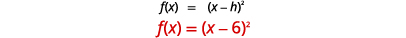
	$.$
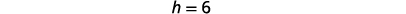Déplace le graphique$f(x)=x^{2}$ vers les bonnes$6$ unités.	$.$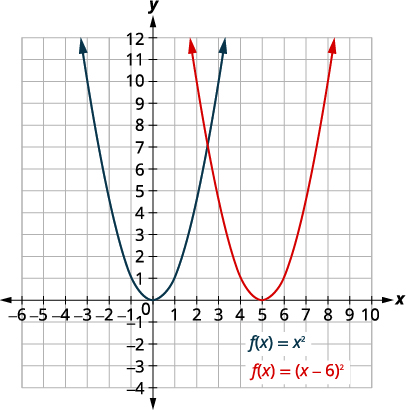

Exercice$\PageIndex{7}$

$f(x)=(x−4)^{2}$Tracez en utilisant un décalage horizontal.

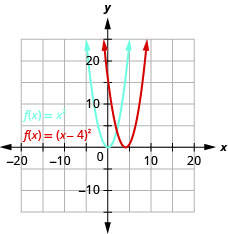
Réponse: $Cette figure montre deux paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. La courbe de gauche est le graphique de f si x est égal à x au carré dont le sommet est (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe droite a été déplacée de 4 unités vers la droite.$
Graphique 9.7.21

Exercice$\PageIndex{8}$

$f(x)=(x+6)^{2}$Tracez en utilisant un décalage horizontal.

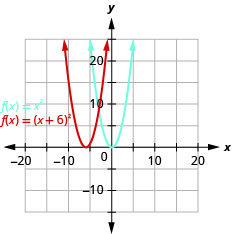
Réponse: $Cette figure montre deux paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. La courbe de droite est le graphe de f si x est égal à x au carré qui a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe de gauche a été déplacée vers la gauche de 6 unités.$
Graphique 9.7.22

Maintenant que nous connaissons l'effet des constantes$h$$k$, nous allons représenter graphiquement une fonction quadratique de la forme$f(x)=(x-h)^{2}+k$ en dessinant d'abord la parabole de base, puis en effectuant un décalage horizontal suivi d'un décalage vertical. Nous pourrions effectuer le décalage vertical suivi du décalage horizontal, mais la plupart des étudiants préfèrent le décalage horizontal suivi du décalage vertical.

Exemple$\PageIndex{5}$

Graphe$f(x)=(x+1)^{2}-2$ utilisant des transformations.

Solution :

Cette fonction impliquera deux transformations et nous avons besoin d'un plan.

Déterminons d'abord les constantes$h, k$.

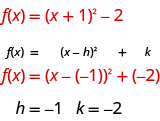
F de x est égal à la quantité x peluche 1 au carré moins 2 est indiqué sur la ligne supérieure et f de x est égal à la quantité x moins h au carré moins k sur la deuxième ligne. L'équation donnée a été modifiée en f si x est égal à la quantité de x moins 1 carré et moins 2 sur la troisième ligne. La dernière ligne indique que h est égal à moins 1 et k est égal à moins 2. — Graphique 9.7.23

La$h$ constante nous donne un décalage horizontal et la$k$ donne un décalage vertical.

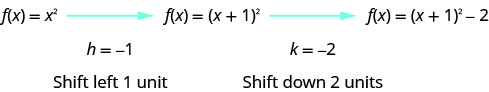
F de x égal x au carré est donné avec une flèche partant de celui-ci pointant vers f de x égale la quantité x plus 1 au carré avec une flèche partant de celui-ci pointant vers f de x égale la quantité x plus 1 au carré moins 2. Les lignes suivantes indiquent que h est égal à moins 1, ce qui signifie un décalage vers la gauche d'une unité et k est égal à moins 2, ce qui signifie un décalage de 2 unités — Graphique 9.7.24

Nous dessinons d'abord le graphique de$f(x)=x^{2}$ sur la grille.

La figure indique sur la première ligne que le graphique de f de x est égal à la quantité x plus 1 au carré est le même que le graphique de f de x égal x au carré mais décalé vers la gauche d'une unité. La deuxième ligne indique que le graphique de f de x est égal à la quantité x plus 1 au carré moins 2 est le même que le graphique de f de x est égal à la quantité x plus 1 au carré mais décalé de 2 unités vers le bas. — Graphique 9.7.25

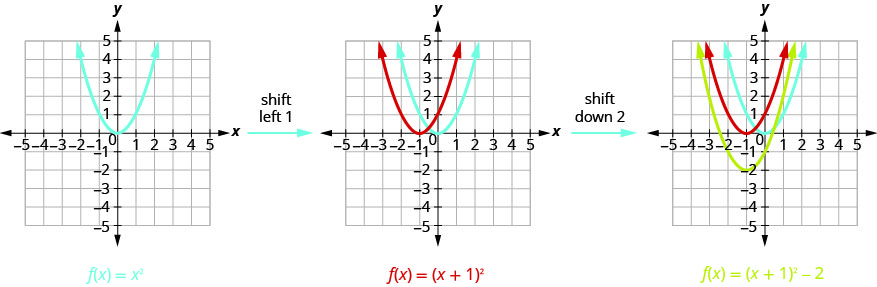
Le premier graphique montre 1 parabole s'ouvrant vers le haut sur le plan de coordonnées x y. C'est le graphe de f si x est égal à x au carré qui a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). En décalant ce graphe de f de x égal x au carré à gauche 1, nous passons au graphique suivant, qui montre le f original de x égal x au carré, puis une autre courbe déplacée vers la gauche d'une unité pour produire f de x égal à la quantité de x plus 1 au carré. En déplaçant f de x égale la quantité de x plus 1 au carré vers le bas de 1, nous passons au graphique final, qui montre que le f initial de x est égal à x au carré et que le f de x est égal à la quantité de x plus 1, puis une autre courbe déplacée vers le bas de 1 pour produire f de x égal à la quantité de x plus 1 au carré moins 2. — Graphique 9.7.26

Exercice$\PageIndex{9}$

Graphe$f(x)=(x+2)^{2}-3$ utilisant des transformations.

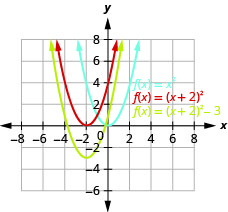
Réponse: $Cette figure montre 3 paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. L'un est le graphe de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). Ensuite, la fonction d'origine est déplacée de 2 unités vers la gauche pour produire f de x égal à la quantité de x plus 2 au carré. La courbe finale est produite en descendant de 3 unités pour produire f de x égal à la quantité de x plus 2 au carré moins 3.$
Graphique 9.7.27

Exercice$\PageIndex{10}$

Graphe$f(x)=(x-3)^{2}+1$ utilisant des transformations.

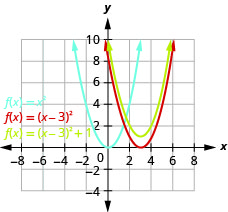
Réponse: $Cette figure montre 3 paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. L'un est le graphe de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). Ensuite, la fonction d'origine est déplacée de 3 unités vers la droite pour produire f de x égal à la quantité de x moins 3 au carré. La courbe finale est produite en remontant d'une unité pour produire f de x égal à la quantité de x moins 3 au carré plus 1.$
Graphique 9.7.28

Représenter graphiquement les fonctions quadratiques du formulaire$f(x)=ax^{2}$

Jusqu'à présent, nous avons représenté graphiquement la fonction quadratique,$f(x)=x^{2}$ puis nous avons vu l'effet de l'inclusion d'une constante$h$ ou$k$ dans l'équation sur le graphe résultant de la nouvelle fonction. Nous allons maintenant explorer l'effet du coefficient$a$ sur le graphe résultant de la nouvelle fonction$f(x)=ax^{2}$.

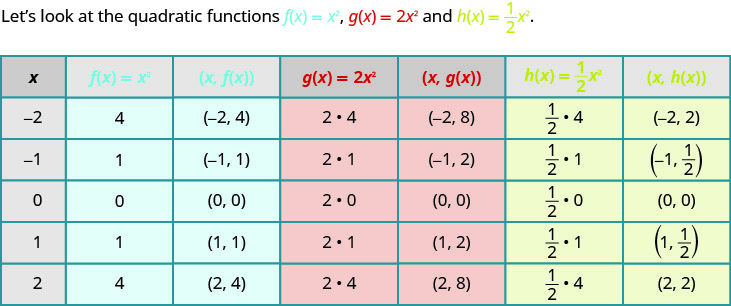
Si nous représentons ces fonctions sous forme graphique, nous pouvons voir l'effet de la constante$a$, en supposant$a>0$.

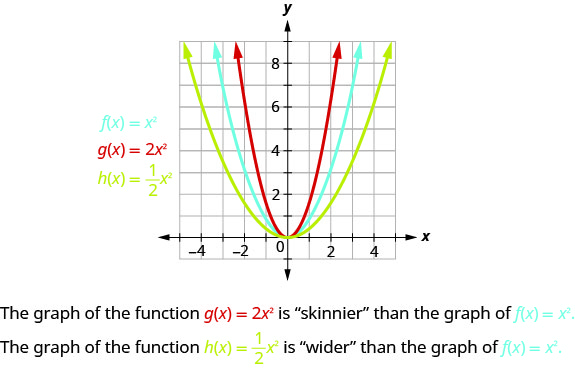
Cette figure montre 3 paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. L'un est le graphe de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe la plus fine de g de x est égale à 2 fois x carré et possède un sommet à (0,0) et les autres points de (moins 1, la moitié) et (1, la moitié). La courbe la plus large, h de x est égal à la moitié du carré, a un sommet à (0,0) et les autres points de (moins 2, 2) et (2,2). — Graphique 9.7.30

Pour représenter graphiquement une fonction avec une constante,$a$ il est plus facile de choisir quelques points$f(x)=x^{2}$ et de multiplier les$y$ valeurs par$a$.

Représentation graphique d'une fonction quadratique de la forme$f(x)=ax^{2}$

Le coefficient de$a$ la fonction$f(x)=ax^{2}$ affecte le graphe en l'$f(x)=x^{2}$étirant ou en le comprimant.

Si$0<|a|<1$, le graphe de$f(x)=ax^{2}$ sera « plus large » que le graphique de$f(x)=x^{2}$.
Si$|a|>1$, le graphique de$f(x)=ax^{2}$ sera « plus fin » que le graphique de$f(x)=x^{2}$.

Exemple$\PageIndex{6}$

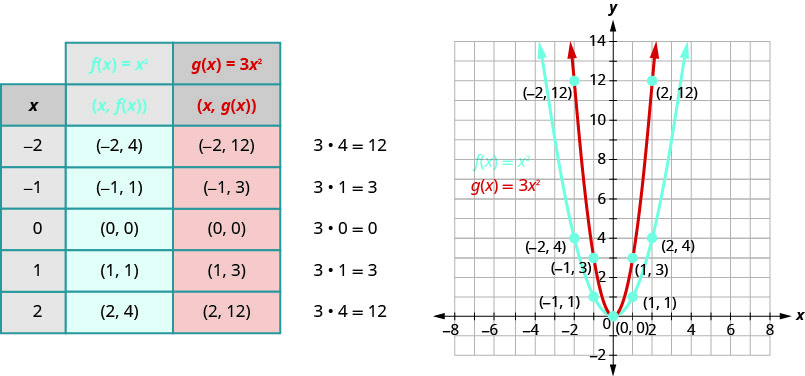
Graphe$f(x)=3x^{2}$.

Solution :

Nous allons représenter graphiquement les fonctions$f(x)=x^{2}$ et$g(x)=3x^{2}$ sur la même grille. Nous allons choisir quelques points,$f(x)=x^{2}$ puis multiplier les$y$ valeurs par pour$3$ obtenir les points pour$g(x)=3x^{2}$.

Le tableau décrit l'effet des constantes sur la fonction de base de x au carré. Le tableau comporte 3 colonnes intitulées x, f de x est égal à x au carré avec la paire ordonnée (x, f de x), et g de x est égal à 3 fois x au carré avec la paire ordonnée (x, g de x). Dans la colonne x, les valeurs indiquées sont négatives 2, négatives 1, 0, 1 et 2. Si f de x est égal à x au carré avec la paire ordonnée (x, f de x), les paires ordonnées (négatif 2, 4), (négatif 1, 1), (0, 0), (1, 1) et (2, 4) sont données. La colonne g de x est égale à 3 fois x au carré avec la paire ordonnée (x, g de x). La colonne contient les paires ordonnées de (négatif 2, 12) parce que 3 fois 4 est égal à 12, (négatif 1, 3) parce que 3 fois 1 est égal à 3, (0, 0) parce que 3 fois 0 est égal à 0, (1, 3) parce que 3 fois 1 est égal à 3, et (2,12) parce que 3 fois 4 est égal à 12. Le graphique à côté du tableau montre deux paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. L'un est le graphe de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points indiqués sur la courbe sont situés à (négatif 2, 4) (négatif 1, 1), (1, 1) et (2,4). La courbe la plus fine de g de x est égale à 3 fois x au carré et possède un sommet à (0,0) et les autres points indiqués par (moins 2, 12), (négatif 1, 3), (1, 3) et (2,12). — Graphique 9.7.31

Exercice$\PageIndex{11}$

Graphe$f(x)=-3x^{2}$.

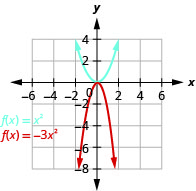
Réponse: $Le graphique montre la parabole s'ouvrant vers le haut sur le plan de coordonnées x y de f si x est égal à x carré dont le sommet est (0, 0). Les autres points indiqués sur la courbe sont situés à (négatif 2, 4) (négatif 1, 1), (1, 1) et (2,4). On voit également une parabole s'ouvrant vers le bas de f de x égale moins 3 fois x au carré. Il a un sommet de (0,0) avec les autres points à (négatif 1, moins 3) et (1, négatif 3)$
Graphique 9.7.32

Exercice$\PageIndex{12}$

Graphe$f(x)=2x^{2}$.

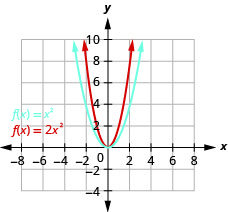
Réponse: $Cette figure montre deux paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. L'un est le graphe de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe la plus fine de f de x est égale à 2 fois x carré et possède un sommet à (0,0) et les autres points de (moins 1, la moitié) et (1, la moitié).$
Graphique 9.7.33

Fonctions quadratiques graphiques à l'aide de transformations

Nous avons appris comment$a, h$ les constantes et$k$ les$f(x)=x^{2}+k, f(x)=(x−h)^{2}$ fonctions$f(x)=ax^{2}$ affectent leurs graphes. Nous pouvons maintenant les assembler et représenter graphiquement les fonctions quadratiques en les$f(x)=ax^{2}+bx+c$ insérant d'abord dans le formulaire$f(x)=a(x−h)^{2}+k$ en complétant le carré. Cette forme est parfois appelée forme de sommet ou forme standard.

Nous devons faire attention à ajouter et à soustraire le nombre du même côté de la fonction pour compléter le carré. Nous ne pouvons pas ajouter le nombre des deux côtés comme nous l'avons fait lorsque nous avons complété le carré avec des équations quadratiques.

Cette figure montre la différence lorsque vous complétez le carré avec une équation quadratique et une fonction quadratique. Pour l'équation quadratique, commencez par x au carré plus 8 fois x plus 6 égale zéro. Soustrayez 6 des deux côtés pour obtenir x au carré plus 8 fois x est égal à moins 6 tout en laissant de l'espace pour compléter le carré. Ensuite, complétez le carré en ajoutant 16 des deux côtés pour obtenir x peluche carrée 8 fois x peluche 16 égale moins 6 peluche 16. Le facteur pour obtenir la quantité x plus 4 au carré est égal à 10. Pour la fonction quadratique, commencez par f si x est égal à x au carré plus 8 fois x plus 6. La deuxième ligne indique de laisser un espace entre les 8 fois x et les 6 afin de compléter le carré. Complétez le carré en ajoutant 16 et en soustrayant 16 du même côté pour obtenir f de x égal x au carré plus 8 fois x peluche 16 plus 6 moins 16. Le facteur pour obtenir f de x est égal à la quantité de x peluche 4 au carré moins 10. — Graphique 9.7.34

Lorsque nous complétons le carré dans une fonction avec un coefficient$x^{2}$ qui n'est pas un, nous devons factoriser ce coefficient uniquement à partir des$x$ termes. Nous ne le prenons pas en compte à partir du terme constant. Il est souvent utile de déplacer le terme constant un peu vers la droite pour qu'il soit plus facile de se concentrer uniquement sur les$x$ termes.

Une fois que nous avons obtenu la constante que nous voulons compléter, nous devons penser à la multiplier par ce coefficient avant de la soustraire.

Exemple$\PageIndex{7}$

Réécrivez le$f(x)=a(x−h)^{2}+k$ formulaire$f(x)=−3x^{2}−6x−1$ en complétant le carré.

Solution :

Tableau 9.7.3
	$.$
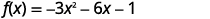Séparez les$x$ termes de la constante.	$.$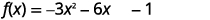
Facturez le coefficient de$x^{2}, -3$.	$.$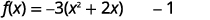
Préparez-vous à terminer le carré.	$.$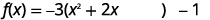
Prenez la moitié$2$ et mettez-la au carré pour compléter le carré$(\frac{1}{2}\cdot 2)^{2}=1$
La constante$1$ complète le carré entre parenthèses, mais les parenthèses sont multipliées par$-3$. Nous ajoutons donc vraiment$-3$. Il faut ensuite ajouter$3$ pour ne pas modifier la valeur de la fonction.	$.$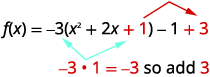
Réécrivez le trinôme sous forme de carré et soustrayez les constantes.	$.$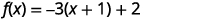
La fonction se trouve désormais dans le$f(x)=a(x-h)^{2}+k$ formulaire.	$.$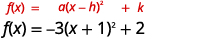

Exercice$\PageIndex{13}$

Réécrivez le$f(x)=a(x−h)^{2}+k$ formulaire$f(x)=−4x^{2}−8x+1$ en complétant le carré.

Réponse: $f(x)=-4(x+1)^{2}+5$

Exercice$\PageIndex{14}$

Réécrivez le$f(x)=a(x−h)^{2}+k$ formulaire$f(x)=2x^{2}−8x+3$ en complétant le carré.

Réponse: $f(x)=2(x-2)^{2}-5$

Une fois que nous avons placé la fonction dans le$f(x)=(x−h)^{2}+k$ formulaire, nous pouvons utiliser les transformations comme nous l'avons fait dans les derniers problèmes. L'exemple suivant nous montrera comment procéder.

Exemple$\PageIndex{8}$

$f(x)=x^{2}+6x+5$Tracez en utilisant des transformations.

Solution :

Étape 1 : Réécrivez la fonction sous forme de$f(x)=a(x-h)^{2}+k$ sommet en complétant le carré.

Tableau 9.7.4
	$.$
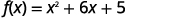Séparez les$x$ termes de la constante.	$.$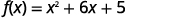
Prenez la moitié$6$ et mettez-la au carré pour compléter le carré. $(\frac{1}{2}\cdot 6)^{2}=9$
Nous ajoutons$9$ et soustrayons$9$ à la fois pour ne pas modifier la valeur de la fonction.	$.$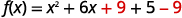
Réécrivez le trinôme sous forme de carré et soustrayez les constantes.	$.$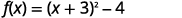
La fonction se trouve désormais dans le$f(x)=(x-h)^{2}+k$ formulaire.	$.$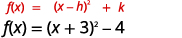

Étape 2 : Représenter graphiquement la fonction à l'aide de transformations

En regardant les$h, k$ valeurs, nous voyons que le graphique prend le graphe de$f(x)=x^{2}$ et le déplace vers les unités de gauche et vers les$3$$4$ unités inférieures.

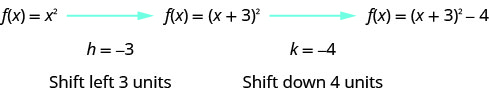
F de x égal x au carré est donné avec une flèche partant de celui-ci pointant vers f de x égale la quantité x plus 3 au carré avec une flèche partant de celui-ci pointant vers f de x égale la quantité x plus 3 au carré moins 4. Les lignes suivantes indiquent que h est égal à moins 3, ce qui signifie décaler vers la gauche de 3 unités et k est égal à moins 4, ce qui signifie un décalage de 4 — Graphique 9.7.47

Nous dessinons d'abord le graphique de$f(x)=x^{2}$ sur la grille.

Pour que le graphe f de x soit égal à la quantité x plus 3 au carré, décalez le graphe de f si x est égal à x carrés vers la gauche de 3 unités. Pour que le graphique f de x soit égal à la quantité x plus 3 au carré moins 4, décalez le graphique de la quantité x plus 3 au carré de 4 unités vers le bas. — Graphique 9.7.48

Exercice$\PageIndex{15}$

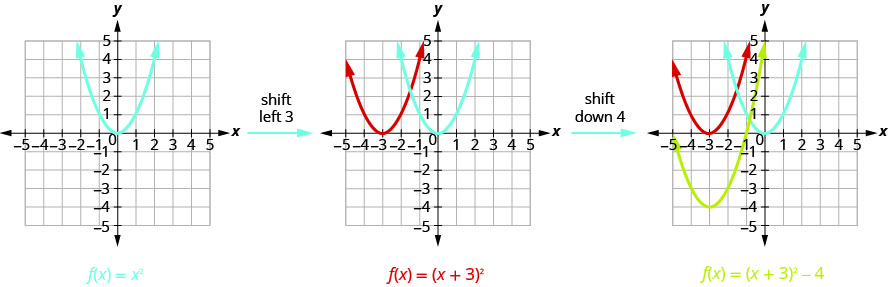
$f(x)=x^{2}+2x-3$Tracez en utilisant des transformations.

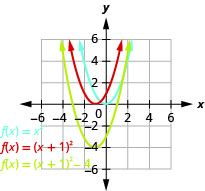
Réponse: $Cette figure montre 3 paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. L'un est le graphe de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe vers la gauche a été déplacée d'une unité vers la gauche pour produire f de x égal à la quantité de x plus 1 au carré. Le troisième graphique a été déplacé de 4 unités vers le bas pour produire f de x égal à la quantité de x plus 1 au carré moins 4.$
Graphique 9.7.50

Exercice$\PageIndex{16}$

$f(x)=x^{2}-8x+12$Tracez en utilisant des transformations.

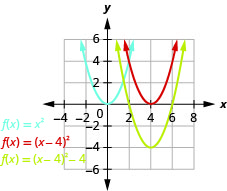
Réponse: $Cette figure montre 3 paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. L'un est le graphe de f si x est égal à x au carré et a un sommet de (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe de droite a été déplacée de 4 unités vers la droite pour produire f de x égal à la quantité de x moins 4 au carré. Le troisième graphique a été déplacé de 4 unités vers le bas pour produire f de x égal à la quantité de x moins 4 au carré moins 4.$
Graphique 9.7.51

Nous listons les étapes pour créer un graphe en fonction quadratique à l'aide de transformations ici.

Tracer une fonction quadratique à l'aide de transformations

Réécrivez la fonction$f(x)=a(x-h)^{2}+k$ sous forme en complétant le carré.
Tracez la fonction en utilisant des transformations.

Exemple$\PageIndex{9}$

$f(x)=-2x^{2}-4x+2$Tracez en utilisant des transformations.

Solution :

Étape 1 : Réécrivez la fonction sous forme de$f(x)=a(x-h)^{2}+k$ sommet en complétant le carré.

Tableau 9.7.5
	$.$
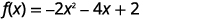Séparez les$x$ termes de la constante.	$.$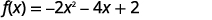
Nous avons besoin que le coefficient$x^{2}$ de soit un. Nous prenons$-2$ en compte les$x$ termes.	$.$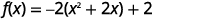
Prenez la moitié$2$ et mettez-la au carré pour compléter le carré. $(\frac{1}{2}\cdot 2)^{2}=1$
Nous ajoutons$1$ pour compléter le carré entre parenthèses, mais les parenthèses sont multipliées par$-2$. Nous ajoutons donc vraiment$-2$. Pour ne pas modifier la valeur de la fonction, nous ajoutons$2$.	$.$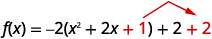
Réécrivez le trinôme sous forme de carré et soustrayez les constantes.	$.$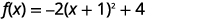
La fonction se trouve désormais dans le$f(x)=a(x-h)^{2}+k$ formulaire.	$.$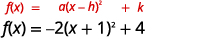

Étape 2 : Représenter graphiquement la fonction à l'aide de transformations

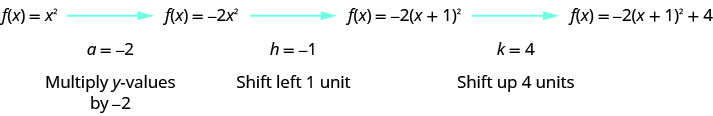
F de x égal x au carré est donné par une flèche partant de celui-ci pointant vers f de x égal à moins 2 fois x au carré avec une flèche partant de celui-ci pointant vers f de x égale moins 2 fois la quantité x plus 1 au carré. Une flèche en sort pour pointer vers f si x est égal à moins 2 fois la quantité x plus 1 au carré plus 4. La ligne suivante indique que a est égal à moins 2, ce qui signifie que vous multipliez les valeurs y par moins 2, puis h est égal à moins 1, ce qui signifie un décalage d'une unité vers la gauche et k est égal à 4, ce qui signifie un décalage de 4 — Graphique 9.7.58

Nous dessinons d'abord le graphique de$f(x)=x^{2}$ sur la grille.

Pour représenter graphiquement f de x égal à moins 2 fois x au carré, multipliez les valeurs y dans la parabole de f si x est égal à x au carré par moins 2. Pour tracer f de x égal moins 2 fois la quantité x plus 1 au carré, décalez le graphe de f si x est égal à moins 2 fois x au carré vers la gauche d'une unité. Pour que le graphe f de x soit égal à moins 2 fois la quantité x plus 1 au carré plus 4, décalez le graphe de f si x est égal à moins 2 fois la quantité x plus 1 au carré de 4 unités. — Graphique 9.7.59

Exercice$\PageIndex{17}$

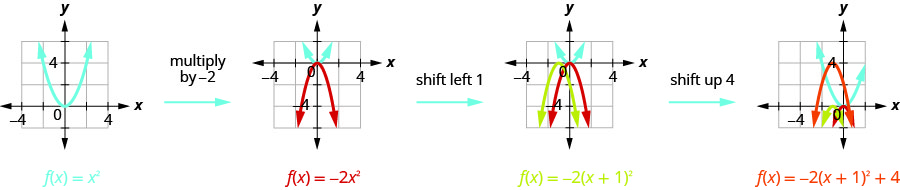
$f(x)=-3x^{2}+12x-4$Tracez en utilisant des transformations.

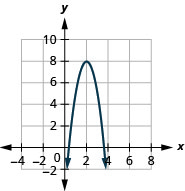
Réponse: $Cette figure montre une parabole s'ouvrant vers le bas sur le plan de coordonnées x y avec un sommet de (2,8) et d'autres points de (1,5) et (3,5).$
Graphique 9.7.61

Exercice$\PageIndex{18}$

$f(x)=−2x^{2}+12x−9$Tracez en utilisant des transformations.

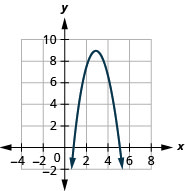
Réponse: $Cette figure montre une parabole s'ouvrant vers le bas sur le plan de coordonnées x y avec un sommet de (3, 9) et d'autres points de (1, 1) et (5, 1).$
Graphique 9.7.62

Maintenant que nous avons terminé le carré pour mettre en$f(x)=a(x−h)^{2}+k$ forme une fonction quadratique, nous pouvons également utiliser cette technique pour représenter graphiquement la fonction en utilisant ses propriétés, comme dans la section précédente.

Si nous regardons les derniers exemples, nous voyons que le sommet est lié aux constantes$h$ et$k$.

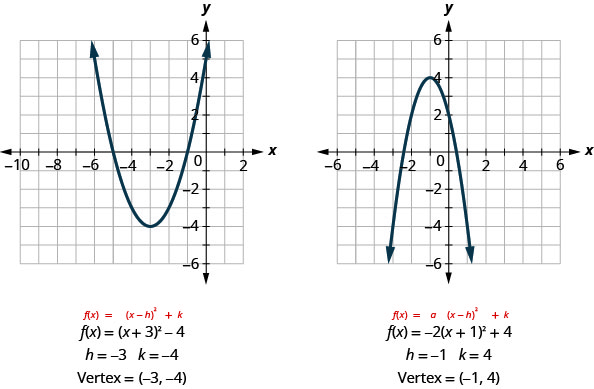
Le premier graphique montre une parabole s'ouvrant vers le haut sur le plan de coordonnées x y avec un sommet de (moins 3, moins 4) avec les autres points de (0, moins 5) et (0, moins 1). Sous le graphique, il montre la forme standard d'une parabole, f de x est égal à la quantité x moins h au carré plus k, l'équation de la parabole f de x étant égale à la quantité de x plus 3 au carré moins 4 où h est égal à moins 3 et k est égal à moins 4. Le deuxième graphique montre une parabole s'ouvrant vers le bas sur le plan de coordonnées x y avec un sommet de (moins 1, 4) et d'autres points de (0,2) et (négatif 2,2). Sous le graphique, il montre la forme standard d'une parabole, f de x est égal à a fois la quantité x moins h au carré plus k, avec l'équation de la parabole f de x égale moins 2 fois la quantité de x plus 1 au carré plus 4 où h est égal à moins 1 et k est égal à 4. — Graphique 9.7.63

Dans chaque cas, le sommet est$(h,k)$. L'axe de symétrie est également la ligne$x=h$.

Nous réécrivons nos étapes de représentation graphique d'une fonction quadratique à l'aide de propriétés correspondant au moment où la fonction est sous$f(x)=a(x−h)^{2}+k$ forme.

Représenter graphiquement une fonction quadratique dans le formulaire à$f(x)=a(x-h)^{2}+k$ l'aide de propriétés

Réécrivez le$f(x)=a(x-h)^{2}+k$ formulaire de la fonction.
Déterminez si la parabole s'ouvre vers le$a>0$ haut ou vers le bas$a<0$.
Trouvez l'axe de symétrie,$x=h$.
Trouvez le sommet,$(h,k$.
Trouvez le$y$ -intercept. Trouvez le point symétrique par rapport à l'$y$intersection -sur l'axe de symétrie.
Trouvez les$x$ -intercepts.
Tracez la parabole.

Exemple$\PageIndex{10}$

Réécrire$f(x)=2 x^{2}+4 x+5$ dans le$f(x)=a(x-h)^{2}+k$ formulaire
Tracez la fonction à l'aide

Solution :

Tableau 9.7.6
Réécrivez la fonction$f(x)=a(x-h)^{2}+k$ sous forme en complétant le carré.	$f(x)=2 x^{2}+4 x+5$
	$f(x)=2\left(x^{2}+2 x\right)+5$
	$f(x)=2\left(x^{2}+2 x+1\right)+5-2$
	$f(x)=2(x+1)^{2}+3$
Identifiez les constantes$a, h, k$.	$a=2 h=-1 k=3$
Depuis$a=2$, la parabole s'ouvre vers le haut.	$.$
L'axe de symétrie est$x=h$.	L'axe de symétrie est$x=-1$.
Le sommet est$(h,k)$.	Le sommet est$(-1,3)$.
Trouvez le$y$ -intercept en trouvant$f(0)$.	$f(0)=2 \cdot 0^{2}+4 \cdot 0+5$
	$f(0)=5$
	$y$-intercepter$(0,5)$
Trouvez le point symétrique par rapport à$(0,5)$ l'axe de symétrie.	$(-2,5)$
Trouvez les$x$ -intercepts.	Le discriminant est négatif, il n'y a donc pas de$x$ -intercepts. Tracez la parabole.
	$.$

Exercice$\PageIndex{19}$

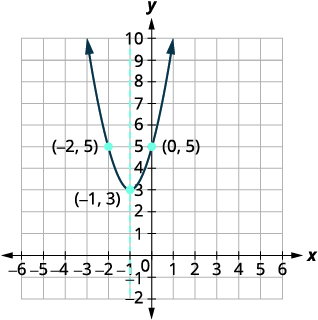Réécrire$f(x)=3 x^{2}-6 x+5$ dans le$f(x)=a(x-h)^{2}+k$ formulaire
Tracez la fonction à l'aide

Réponse

$f(x)=3(x-1)^{2}+2$
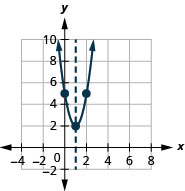
$Le graphique présenté est une parabole orientée vers le haut avec un sommet (1, 2) et une intersection y (0, 5). L'axe de symétrie est indiqué, x est égal à 1.$
Graphique 9.7.66

Exercice$\PageIndex{20}$

Réécrire$f(x)=-2 x^{2}+8 x-7$ dans le$f(x)=a(x-h)^{2}+k$ formulaire
Tracez la fonction à l'aide

Réponse

$f(x)=-2(x-2)^{2}+1$
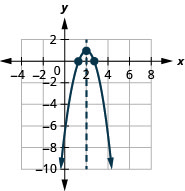
$Le graphique présenté est une parabole orientée vers le bas avec un sommet (2, 1) et des points d'intersection en X (1, 0) et (3, 0). L'axe de symétrie est indiqué, x est égal à 2.$
Graphique 9.7.67

Trouver une fonction quadratique à partir de son graphe

Jusqu'à présent, nous avons commencé par une fonction, puis nous avons trouvé son graphique.

Nous allons maintenant inverser le processus. En commençant par le graphique, nous allons trouver la fonction.

Exemple$\PageIndex{11}$

Déterminez la fonction quadratique dont le graphique est affiché.

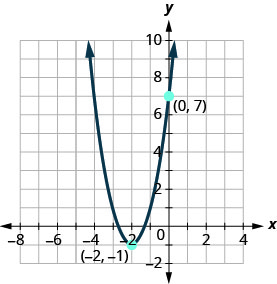
Le graphique présenté est une parabole orientée vers le haut avec un sommet (négatif 2, négatif 1) et une intersection y (0, 7). — Graphique 9.7.68

Solution :

Comme il est quadratique, nous commençons par le$f(x)=a(x−h)^{2}+k$ formulaire.

Le sommet,$(h,k)$, est$(−2,−1)$ tel$h=−2$ et$k=−1$.

$f(x)=a(x-(-2))^{2}-1$

Pour le trouver$a$, nous utilisons l'$y$option -intercept,$(0,7)$.

Donc$f(0)=7$.

$7=a(0+2)^{2}-1$

Résolvez pour$a$.

$\begin{array}{l}{7=4 a-1} \\ {8=4 a} \\ {2=a}\end{array}$

Écrivez la fonction.

$f(x)=a(x-h)^{2}+k$

Remplacez par$h=-2, k=-1$ et$a=2$.

$f(x)=2(x+2)^{2}-1$

Exercice$\PageIndex{21}$

Écrivez la fonction quadratique$f(x)=a(x−h)^{2}+k$ sous la forme dont le graphique est affiché.

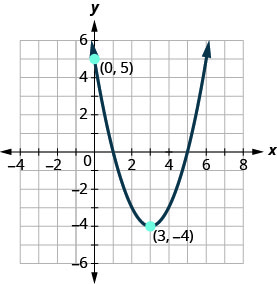
Le graphique présenté est une parabole orientée vers le haut avec sommet (3, négatif 4) et intersection y (0, 5). — Graphique 9.7.69

Réponse: $f(x)=(x-3)^{2}-4$

Exercice$\PageIndex{22}$

Déterminez la fonction quadratique dont le graphique est affiché.

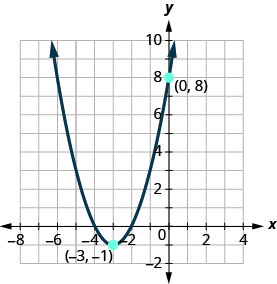
Le graphique présenté est une parabole orientée vers le haut avec un sommet (négatif 3, négatif 1) et une intersection y (0, 8). — Graphique 9.7.70

Réponse: $f(x)=(x+3)^{2}-1$

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à représenter graphiquement des fonctions quadratiques à l'aide de transformations.

Concepts clés

Tracez une fonction quadratique du formulaire à$f(x)=x^{2}+k$ l'aide d'un décalage vertical
- Le graphe de$f(x)=x^{2}+k$ déplace le graphe des$k$ unités$f(x)=x^{2}$ verticales.
  - Si$k>0$, déplacez la parabole verticalement vers le haut$k$ d'unités.
  - Si$k<0$, déplacez la parabole verticalement vers le bas en$|k|$ unités.
Tracez une fonction quadratique du formulaire à$f(x)=(x−h)^{2}$ l'aide d'un décalage horizontal
- Le graphe de$f(x)=(x−h)^{2}$ déplace le graphe des$h$ unités$f(x)=x^{2}$ horizontales.
  - Si$h>0$, déplacez la parabole horizontalement vers la gauche en$h$ unités.
  - Si$h<0$, décalez la parabole horizontalement en$|h|$ unités droites.
Graphe d'une fonction quadratique de la forme$f(x)=ax^{2}$
- Le coefficient de$a$ la fonction$f(x)=ax^{2}$ affecte le graphe en l'$f(x)=x^{2}$étirant ou en le comprimant.
  Si$0<|a|<1$, alors le graphe de$f(x)=ax^{2}$ sera « plus large » que le graphique de$f(x)=x^{2}$.
  Si$|a|>1$, alors le graphique de$f(x)=ax^{2}$ sera « plus fin » que le graphique de$f(x)=x^{2}$.
Comment représenter graphiquement une fonction quadratique à l'aide de transformations
1. Réécrivez la fonction$f(x)=a(x−h)^{2}+k$ sous forme en complétant le carré.
2. Tracez la fonction en utilisant des transformations.
Tracez une fonction quadratique sous la forme d'un sommet à$f(x)=a(x−h)^{2}+k$ l'aide de propriétés
1. Réécrivez la fonction dans le$f(x)=a(x−h)^{2}+k$ formulaire.
2. Déterminez si la parabole s'ouvre vers le$a>0$ haut ou vers le bas$a<0$.
3. Trouvez l'axe de symétrie,$x=h$.
4. Trouvez le sommet,$(h,k)$.
5. Trouvez le$y$ -intercept. Trouvez le point symétrique par rapport à l'$y$intersection -sur l'axe de symétrie.
6. Trouvez les$x$ -intercepts, si possible.
7. Tracez la parabole.

Réécrivez la fonction\(f(x)=a(x-h)^{2}+k\) sous forme en complétant le carré.	\(f(x)=2 x^{2}+4 x+5\)
	\(f(x)=2\left(x^{2}+2 x\right)+5\)
	\(f(x)=2\left(x^{2}+2 x+1\right)+5-2\)
	\(f(x)=2(x+1)^{2}+3\)
Identifiez les constantes\(a, h, k\).	\(a=2 h=-1 k=3\)
Depuis\(a=2\), la parabole s'ouvre vers le haut.	$.$
L'axe de symétrie est\(x=h\).	L'axe de symétrie est\(x=-1\).
Le sommet est\((h,k)\).	Le sommet est\((-1,3)\).
Trouvez le\(y\) -intercept en trouvant\(f(0)\).	\(f(0)=2 \cdot 0^{2}+4 \cdot 0+5\)
	\(f(0)=5\)
	\(y\)-intercepter\((0,5)\)
Trouvez le point symétrique par rapport à\((0,5)\) l'axe de symétrie.	\((-2,5)\)
Trouvez les\(x\) -intercepts.	Le discriminant est négatif, il n'y a donc pas de\(x\) -intercepts. Tracez la parabole.
	$.$

Exemple\(\PageIndex{1}\)

Exercice\(\PageIndex{1}\)

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{2}\)

Exercice\(\PageIndex{3}\)

Exercice\(\PageIndex{4}\)

Exemple\(\PageIndex{3}\)

Exercice\(\PageIndex{5}\)

Exercice\(\PageIndex{6}\)

Exemple\(\PageIndex{4}\)

Exercice\(\PageIndex{7}\)

Exercice\(\PageIndex{8}\)

Exemple\(\PageIndex{5}\)

Exercice\(\PageIndex{9}\)

Exercice\(\PageIndex{10}\)

Exemple\(\PageIndex{6}\)

Exercice\(\PageIndex{11}\)

Exercice\(\PageIndex{12}\)

Exemple\(\PageIndex{7}\)

Exercice\(\PageIndex{13}\)

Exercice\(\PageIndex{14}\)

Exemple\(\PageIndex{8}\)

Exercice\(\PageIndex{15}\)

Exercice\(\PageIndex{16}\)

Exemple\(\PageIndex{9}\)

Exercice\(\PageIndex{17}\)

Exercice\(\PageIndex{18}\)

Exemple\(\PageIndex{10}\)

Exercice\(\PageIndex{19}\)

Exercice\(\PageIndex{20}\)

Exemple\(\PageIndex{11}\)

Exercice\(\PageIndex{21}\)

Exercice\(\PageIndex{22}\)

Nous dessinons d'abord le graphique de\(f(x)=x^{2}\) sur la grille.	$Cette figure montre une parabole s'ouvrant vers le haut sur le plan de coordonnées x y avec un sommet de (0, 0) avec les autres points de la courbe situés à (moins 1, 1) et (1, 1). C'est le graphe de f si x est égal à x au carré.$
Déterminez\(k\).	$.$
	$.$
Déplace le graphique\(f(x)=x^{2}\) vers le bas\(3\).	$Cette figure montre deux paraboles s'ouvrant vers le haut sur le plan de coordonnées x y. La courbe supérieure est le graphique de f si x est égal à x au carré dont le sommet est (0, 0). Les autres points de la courbe sont situés à (moins 1, 1) et (1, 1). La courbe inférieure a été déplacée de 3 unités vers le bas.$

Nous dessinons d'abord le graphique de\(f(x)=x^{2}\) sur la grille.	$.$
Déterminez\(h\).	$.$
	$.$
Déplace le graphique\(f(x)=x^{2}\) vers les bonnes\(6\) unités.	$.$

	$.$
Séparez les\(x\) termes de la constante.	$.$
Facturez le coefficient de\(x^{2}, -3\).	$.$
Préparez-vous à terminer le carré.	$.$
Prenez la moitié\(2\) et mettez-la au carré pour compléter le carré\((\frac{1}{2}\cdot 2)^{2}=1\)
La constante\(1\) complète le carré entre parenthèses, mais les parenthèses sont multipliées par\(-3\). Nous ajoutons donc vraiment\(-3\). Il faut ensuite ajouter\(3\) pour ne pas modifier la valeur de la fonction.	$.$
Réécrivez le trinôme sous forme de carré et soustrayez les constantes.	$.$
La fonction se trouve désormais dans le\(f(x)=a(x-h)^{2}+k\) formulaire.	$.$

	$.$
Séparez les\(x\) termes de la constante.	$.$
Prenez la moitié\(6\) et mettez-la au carré pour compléter le carré. \((\frac{1}{2}\cdot 6)^{2}=9\)
Nous ajoutons\(9\) et soustrayons\(9\) à la fois pour ne pas modifier la valeur de la fonction.	$.$
Réécrivez le trinôme sous forme de carré et soustrayez les constantes.	$.$
La fonction se trouve désormais dans le\(f(x)=(x-h)^{2}+k\) formulaire.	$.$

	$.$
Séparez les\(x\) termes de la constante.	$.$
Nous avons besoin que le coefficient\(x^{2}\) de soit un. Nous prenons\(-2\) en compte les\(x\) termes.	$.$
Prenez la moitié\(2\) et mettez-la au carré pour compléter le carré. \((\frac{1}{2}\cdot 2)^{2}=1\)
Nous ajoutons\(1\) pour compléter le carré entre parenthèses, mais les parenthèses sont multipliées par\(-2\). Nous ajoutons donc vraiment\(-2\). Pour ne pas modifier la valeur de la fonction, nous ajoutons\(2\).	$.$
Réécrivez le trinôme sous forme de carré et soustrayez les constantes.	$.$
La fonction se trouve désormais dans le\(f(x)=a(x-h)^{2}+k\) formulaire.	$.$

Objectifs d'apprentissage

Représenter graphiquement les fonctions quadratiques du formulaire\(f(x)=x^{2}+k\)

Exemple\(\PageIndex{1}\)

Exercice\(\PageIndex{1}\)

Exercice\(\PageIndex{2}\)

Tracez une fonction quadratique du formulaire à\(f(x)=x^{2}+k\) l'aide d'un décalage vertical

Exemple\(\PageIndex{2}\)

Exercice\(\PageIndex{3}\)

Exercice\(\PageIndex{4}\)

Représenter graphiquement les fonctions quadratiques du formulaire\(f(x)=(x-h)^{2}\)

Exemple\(\PageIndex{3}\)

Exercice\(\PageIndex{5}\)

Exercice\(\PageIndex{6}\)

Tracez une fonction quadratique du formulaire à\(f(x)=(x-h)^{2}\) l'aide d'un décalage horizontal

Exemple\(\PageIndex{4}\)

Exercice\(\PageIndex{7}\)

Exercice\(\PageIndex{8}\)

Exemple\(\PageIndex{5}\)

Exercice\(\PageIndex{9}\)

Exercice\(\PageIndex{10}\)

Représenter graphiquement les fonctions quadratiques du formulaire\(f(x)=ax^{2}\)

Représentation graphique d'une fonction quadratique de la forme\(f(x)=ax^{2}\)

Exemple\(\PageIndex{6}\)

Exercice\(\PageIndex{11}\)

Exercice\(\PageIndex{12}\)

Fonctions quadratiques graphiques à l'aide de transformations

Exemple\(\PageIndex{7}\)

Exercice\(\PageIndex{13}\)

Exercice\(\PageIndex{14}\)

Exemple\(\PageIndex{8}\)

Exercice\(\PageIndex{15}\)

Exercice\(\PageIndex{16}\)

Tracer une fonction quadratique à l'aide de transformations

Exemple\(\PageIndex{9}\)

Exercice\(\PageIndex{17}\)

Exercice\(\PageIndex{18}\)

Représenter graphiquement une fonction quadratique dans le formulaire à\(f(x)=a(x-h)^{2}+k\) l'aide de propriétés

Exemple\(\PageIndex{10}\)

Exercice\(\PageIndex{19}\)

Exercice\(\PageIndex{20}\)

Trouver une fonction quadratique à partir de son graphe

Exemple\(\PageIndex{11}\)

Exercice\(\PageIndex{21}\)

Exercice\(\PageIndex{22}\)

Concepts clés