Skip to main content
Global

9.7E : Tracez des fonctions quadratiques à l'aide de propriétés (exercices)

  1. Last updated
  2. Save as PDF
  • Page ID
    194389

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La pratique rend parfait

    Exercices 1 à 4 : Reconnaître le graphe d'une fonction quadratique

    Dans les exercices suivants, tracez les fonctions en traçant des points.

    1. \(f(x)=x^{2}+3\)

    2. \(f(x)=x^{2}-3\)

    3. \(y=-x^{2}+1\)

    4. \(f(x)=-x^{2}-1\)

    Réponse

    1.

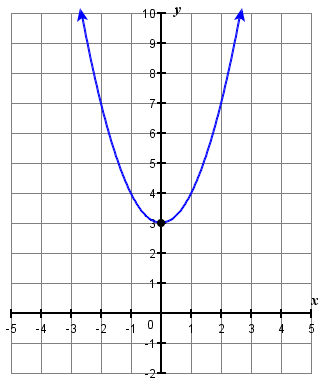
    clipboard_eb78a0f78325e7c8a9cceea709788ca1d.png

    3.

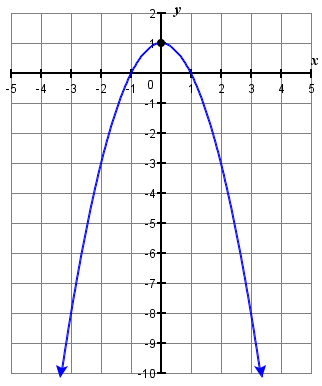
    clipboard_ef318ed788d73edacb2b69f9a778e9ce9.png

    Exercices 5 à 8 : Reconnaître le graphe d'une fonction quadratique

    Pour chacun des exercices suivants, déterminez si la parabole s'ouvre vers le haut ou vers le bas.

    5. a.\(f(x)=-2 x^{2}-6 x-7\) b.\(f(x)=6 x^{2}+2 x+3\)

    6. a.\(f(x)=4 x^{2}+x-4\) b.\(f(x)=-9 x^{2}-24 x-16\)

    7. a.\(f(x)=-3 x^{2}+5 x-1\) b.\(f(x)=2 x^{2}-4 x+5\)

    8. a.\(f(x)=x^{2}+3 x-4\) b.\(f(x)=-4 x^{2}-12 x-9\)

    Réponse

    5. a. en bas b. en haut

    7. a. en bas b. en haut

    Exercices 9 à 12 : Déterminer l'axe de symétrie et le sommet d'une parabole

    Dans les fonctions suivantes, recherchez

    1. L'équation de l'axe de symétrie
    2. Le sommet de son graphe

    9. \(f(x)=x^{2}+8 x-1\)

    10. \(f(x)=x^{2}+10 x+25\)

    11. \(f(x)=-x^{2}+2 x+5\)

    12. \(f(x)=-2 x^{2}-8 x-3\)

    Réponse

    9. a. Axe de symétrie :\(x=-4\) b. Sommet :\((-4,-17)\)

    11. a. Axe de symétrie :\(x=1\) b. Sommet :\((1,2)\)

    Exercices 13 à 24 : Trouvez les points d'intersection d'une parabole

    Dans les exercices suivants, trouvez les points d'intersection de la parabole dont la fonction est donnée.

    13. \(f(x)=x^{2}+7 x+6\)

    14. \(f(x)=x^{2}+10 x-11\)

    15. \(f(x)=x^{2}+8 x+12\)

    16. \(f(x)=x^{2}+5 x+6\)

    17. \(f(x)=-x^{2}+8 x-19\)

    18. \(f(x)=-3 x^{2}+x-1\)

    19. \(f(x)=x^{2}+6 x+13\)

    20. \(f(x)=x^{2}+8 x+12\)

    21. \(f(x)=4 x^{2}-20 x+25\)

    22. \(f(x)=-x^{2}-14 x-49\)

    23. \(f(x)=-x^{2}-6 x-9\)

    24. \(f(x)=4 x^{2}+4 x+1\)

    Réponse

    13. \(y\)-intercepter :\((0,6)\) ;\(x\) -interception (s) :\((-1,0), (-6,0)\)

    15. \(y\)-intercepter :\((0,12)\) ;\(x\) -interception (s) :\((-2,0), (-6,0)\)

    17. \(y\)-intercept :\((0,-19)\) ;\(x\) -intercept (s) : aucun

    19. \(y\)-intercept :\((0,13)\) ;\(x\) -intercept (s) : aucun

    21. \(y\)-intercepter :\((0,-16)\) ;\(x\) -interception (s) :\((\frac{5}{2},0)\)

    23. \(y\)-intercepter :\((0,9)\) ;\(x\) -interception (s) :\((-3,0)\)

    Exercices 25 à 42 : Représenter graphiquement des fonctions quadratiques à l'aide

    Dans les exercices suivants, tracez la fonction sous forme graphique à l'aide de ses propriétés.

    25. \(f(x)=x^{2}+6 x+5\)

    26. \(f(x)=x^{2}+4 x-12\)

    27. \(f(x)=x^{2}+4 x+3\)

    28. \(f(x)=x^{2}-6 x+8\)

    29. \(f(x)=9 x^{2}+12 x+4\)

    30. \(f(x)=-x^{2}+8 x-16\)

    31. \(f(x)=-x^{2}+2 x-7\)

    32. \(f(x)=5 x^{2}+2\)

    33. \(f(x)=2 x^{2}-4 x+1\)

    34. \(f(x)=3 x^{2}-6 x-1\)

    35. \(f(x)=2 x^{2}-4 x+2\)

    36. \(f(x)=-4 x^{2}-6 x-2\)

    37. \(f(x)=-x^{2}-4 x+2\)

    38. \(f(x)=x^{2}+6 x+8\)

    39. \(f(x)=5 x^{2}-10 x+8\)

    40. \(f(x)=-16 x^{2}+24 x-9\)

    41. \(f(x)=3 x^{2}+18 x+20\)

    42. \(f(x)=-2 x^{2}+8 x-10\)

    Réponse

    25.

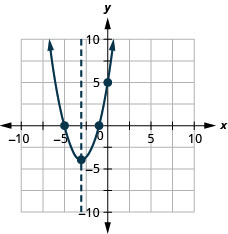
    Cette figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 10 à 10. La parabole a un sommet en (négatif 3, négatif 4). L'intersection y, point (0, 5), est tracée de même que les interceptions en X (négatif 5, 0) et (négatif 1, 0).
    Graphique 9.6.136

    27.

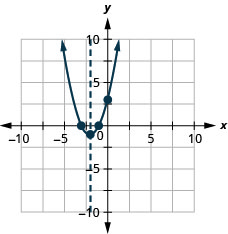
    Cette figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 10 à 10. La parabole a un sommet en (négatif 2, négatif 1). L'intersection y, point (0, 3), est tracée de même que les interceptions en X (négatif 3, 0) et (négatif 1, 0).
    Graphique 9.6.137

    29.

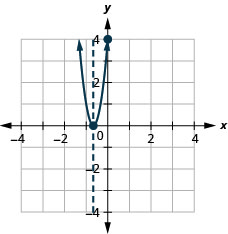
    Cette figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 4 à 4. L'axe Y du plan va de moins 4 à 4. La parabole a un sommet à (moins 2 tiers, 0). L'intersection Y, point (0, 4), est tracée. L'axe de symétrie, x est égal à moins 2 tiers, est tracé sous la forme d'une ligne verticale en pointillés.
    Graphique 9.6.138

    31.

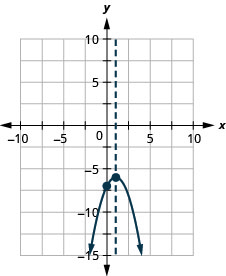
    Cette figure montre une parabole s'ouvrant vers le bas tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 15 à 10. La parabole a un sommet en (1, négatif 6). L'intersection Y, point (0, moins 7), est tracée. L'axe de symétrie, x est égal à 1, est tracé sous la forme d'une ligne verticale en pointillés.
    Graphique 9.6.139

    33.

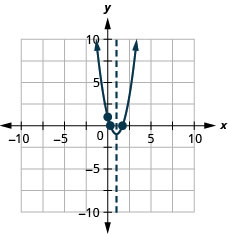
    Cette figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 10 à 10. La parabole a un sommet en (1, négatif 1). L'intersection y, point (0, 1), est tracée comme le sont les interceptions X, approximativement (0,3, 0) et (1,7, 0). L'axe de symétrie est la ligne verticale x égale à 1, tracée en pointillés.
    Graphique 9.6.140

    35.

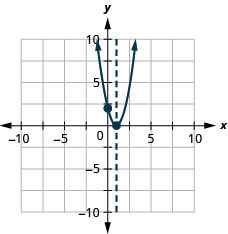
    Cette figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 10 à 10. La parabole a un sommet en (1, 0). Ce point est la seule intersection X. L'intersection Y, point (0, 2), est tracée. L'axe de symétrie est la ligne verticale x égale à 1, tracée en pointillés.
    Graphique 9.6.141

    37.

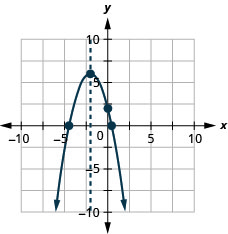
    Cette figure montre une parabole s'ouvrant vers le bas tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 10 à 10. La parabole a un sommet en (négatif 2, 6). L'intersection y, point (0, 2), est tracée comme le sont les interceptions X, approximativement (négatif 4,4, 0) et (0,4, 0). L'axe de symétrie est la ligne verticale x égale à 2, tracée en pointillés.
    Graphique 9.6.142

    39.

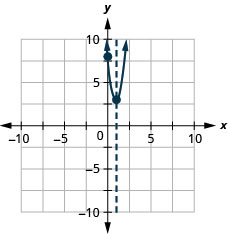
    Cette figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 10 à 10. La parabole a un sommet en (1, 3). L'intersection y, point (0, 8), est tracée ; il n'y a pas d'intersection X. L'axe de symétrie est la ligne verticale x égale à 1, tracée en pointillés.
    Graphique 9.6.143

    41.

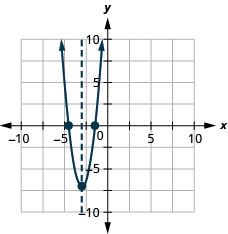
    Cette figure montre une parabole s'ouvrant vers le haut tracée sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe Y du plan va de moins 10 à 10. La parabole a un sommet en (négatif 3, négatif 7). Les points d'intersection X sont tracés aux points approximatifs (moins 4,5, 0) et (moins 1,5, 0). L'axe de symétrie est la ligne verticale x égale moins 3, tracée en pointillés.
    Graphique 9.6.144
    Exercices 43 à 48 : Résolvez les applications maximales et minimales

    Dans les exercices suivants, déterminez la valeur maximale ou minimale de chaque fonction.

    43. \(f(x)=2 x^{2}+x-1\)

    44. \(y=-4 x^{2}+12 x-5\)

    45. \(y=x^{2}-6 x+15\)

    46. \(y=-x^{2}+4 x-5\)

    47. \(y=-9 x^{2}+16\)

    48. \(y=4 x^{2}-49\)

    Réponse

    43. La valeur minimale est\(−\frac{9}{8}\) quand\(x=−\frac{1}{4}\).

    45. La valeur maximale est\(6\) quand\(x=3\).

    47. La valeur maximale est\(16\) quand\(x=0\).

    Exercices 49 à 60 : Résolvez les applications maximales et minimales

    Dans les exercices suivants, résolvez. Arrondissez les réponses au dixième le plus proche.

    49. Une flèche est tirée verticalement vers le haut depuis une plate-forme de\(45\) pieds de haut à une vitesse de pieds\(168\) par seconde. Utilisez la fonction quadratique\(h(t)=-16 t^{2}+168 t+45\) pour déterminer le temps qu'il faudra à la flèche pour atteindre sa hauteur maximale, puis trouvez la hauteur maximale.

    50. Une pierre est projetée verticalement vers le haut à partir d'une plate-forme d'une hauteur de\(20\) pieds à une vitesse de\(160\) pieds par seconde. Utilisez la fonction quadratique\(h(t)=-16 t^{2}+160 t+20\) pour déterminer le temps qu'il faudra à la pierre pour atteindre sa hauteur maximale, puis déterminez la hauteur maximale.

    51. Une balle est lancée verticalement vers le haut depuis le sol avec une vitesse initiale de\(109\) pieds/seconde. Utilisez la fonction quadratique\(h(t)=-16 t^{2}+109 t+0\) pour déterminer le temps qu'il faudra à la balle pour atteindre sa hauteur maximale, puis déterminez la hauteur maximale.

    52. Une balle est lancée verticalement vers le haut depuis le sol avec une vitesse initiale de\(122\) pieds/seconde. Utilisez la fonction quadratique\(h(t)=-16 t^{2}+122 t+0\) pour déterminer le temps qu'il faudra à la balle pour atteindre sa hauteur maximale, puis déterminez la hauteur maximale.

    53. Un propriétaire de magasin d'informatique estime qu'en facturant des\(x\) dollars chacun pour un ordinateur donné, il peut vendre\(40 − x\) des ordinateurs chaque semaine. La fonction quadratique\(R(x)=-x^{2}+40 x\) est utilisée pour trouver le revenu\(R\), reçu lorsque le prix de vente d'un ordinateur est\(x\), trouver le prix de vente qui lui donnera le revenu maximum, puis trouver le montant du revenu maximum.

    54. Un détaillant qui vend des sacs à dos estime qu'en les vendant à des\(x\) dollars chacun, il sera en mesure de vendre des\(100 − x\) sacs à dos par mois. La fonction quadratique\(R(x)=-x^{2}+100 x\) est utilisée pour trouver le\(R\), reçu lorsque le prix de vente d'un sac à dos est\(x\). Trouvez le prix de vente qui lui donnera le maximum de revenus, puis trouvez le montant du revenu maximum.

    55. Un détaillant qui vend des bottes de mode estime qu'en les vendant à des\(x\) dollars chacune, il sera en mesure de vendre des\(70 − x\) bottes par semaine. Utilisez la fonction quadratique\(R(x)=-x^{2}+70 x\) pour déterminer les revenus perçus lorsque le prix de vente moyen d'une paire de bottes de mode est de\(x\). Trouvez le prix de vente qui lui donnera le maximum de revenus, puis trouvez le montant du revenu maximum par jour.

    56. Une entreprise de téléphonie mobile estime qu'en facturant des\(x\) dollars chacun pour un certain téléphone portable, elle peut vendre des\(8 − x\) téléphones portables par jour. Utilisez la fonction quadratique\(R(x)=-x^{2}+8 x\) pour trouver les revenus perçus par jour lorsque le prix de vente d'un téléphone portable est\(x\). Trouvez le prix de vente qui leur donnera le revenu maximum par jour, puis déterminez le montant du revenu maximum.

    57. Un éleveur va clôturer trois côtés d'un corral au bord d'une rivière. Il doit maximiser la zone du corral en utilisant des\(240\) pieds de clôture. L'équation quadratique\(A(x)=x(240-2 x)\) donne la superficie du corral\(A\), pour la longueur\(x\), du corral le long de la rivière. Trouvez la longueur du corral le long de la rivière qui donnera la superficie maximale, puis trouvez la superficie maximale du corral.

    58. Un vétérinaire enferme une aire de course extérieure rectangulaire contre son bâtiment pour les chiens dont il s'occupe. Il doit maximiser la surface en utilisant des\(100\) pieds de clôture. La fonction quadratique\(A(x)=x(100-2 x)\) donne la superficie du parc à chiens sur toute la longueur du bâtiment qui bordera le parc à chiens.\(A\)\(x\) Déterminez la longueur du bâtiment qui doit border le parc à chiens pour obtenir la superficie maximale, puis déterminez la surface maximale du parc à chiens.

    59. Un propriétaire foncier prévoit de construire un patio rectangulaire clôturé derrière son garage, en utilisant son garage comme « mur ». Il veut maximiser la surface en utilisant des\(80\) pieds de clôture. La fonction quadratique\(A(x)=x(80-2 x)\) donne la surface du patio, où\(x\) est la largeur d'un côté. Trouvez la surface maximale du patio.

    60. Une famille de trois jeunes enfants vient d'emménager dans une maison dont la cour n'est pas clôturée. L'ancien propriétaire leur a donné des\(300\) pieds de clôture à utiliser pour clôturer une partie de leur jardin. Utilisez la fonction quadratique\(A(x)=x(300-2 x)\) pour déterminer la superficie maximale de la cour clôturée.

    Réponse

    49. En\(5.3\) quelques secondes, la flèche atteindra une hauteur maximale de\(486\) pieds.

    51. En\(3.4\) quelques secondes, le ballon atteindra sa hauteur maximale de\(185.6\) pieds.

    53. \(20\)les ordinateurs donneront le maximum de dollars\(400\) en reçus.

    55. Il pourra vendre des\(35\) paires de bottes au maximum de $\(1,225\).

    57. La longueur du côté le long de la rivière du corral est de\(120\) pieds et la superficie maximale est de pieds\(7,200\) carrés.

    59. La surface maximale du patio est de\(800\) pieds.

    Exercices 61 à 64 : Exercices d'écriture

    61. En quoi les graphes des fonctions\(f(x)=x^{2}\)\(f(x)=x^{2}−1\) diffèrent-ils ? Nous les avons illustrés au début de cette section. Quelle est la différence entre leurs graphiques ? En quoi leurs graphiques sont-ils les mêmes ?

    62. Expliquez comment trouver le sommet d'une parabole.

    63. Expliquez comment trouver les points d'intersection d'une parabole.

    64. Comment utiliser le discriminant lorsque vous tracez une fonction quadratique ?

    Réponse

    1. Les réponses peuvent varier.

    3. Les réponses peuvent varier.

    Auto-vérification

    a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

    Ce tableau fournit une liste de contrôle pour évaluer la maîtrise des objectifs de cette section. Choisissez comment répondriez-vous à la déclaration “Je peux reconnaître le graphique d'une équation quadratique.†“En toute confiance, †“Avec de l'aide, †ou “Non, je ne comprends pasâ €™ Choisissez comment répondriez-vous à la déclaration “Je peux trouver l'axe de symétrie et le sommet d'une parabole. †“En toute confiance, †€ œavec un peu d'aide, †ou “Non, je ne l'obtenezâ €™. Choisissez comment répondriez-vous à la déclaration “Je peux trouver les interceptions d'une parabole. †“En toute confiance, †“Avec de l'aide, †ou “Non, je ne l'obtenezâ €™ t obtenir.†Choisissez comment répondriez-vous à la déclaration “Je peux tracer un graphique quadratique équations statiques dans deux variables.††œEn toute confiance, †“Avec de l'aide, †ou “Non, je ne comprends pasâ €™. Choisissez comment répondriez-vous à la déclaration “Je peux résoudre le maximum et le minimum de demandes. †“En toute confiance, †“Avec de l'aide, †ou “Non, je ne comprends pasâ €™ t
    Graphique 9.6.145

    b. Après avoir examiné la liste de contrôle, pensez-vous être bien préparé pour la section suivante ? Pourquoi ou pourquoi pas ?