9.7 : Représenter graphiquement des fonctions quadratiques à l'aide
- Page ID
- 194383
À la fin de cette section, vous serez en mesure de :
- Reconnaître le graphe d'une fonction quadratique
- Trouvez l'axe de symétrie et le sommet d'une parabole
- Trouvez les points d'intersection d'une parabole
- Représenter des fonctions quadratiques sous forme graphique à
- Résolvez les applications maximales et minimales
Avant de commencer, répondez à ce questionnaire de préparation.
- Tracez la fonction\(f(x)=x^{2}\) en traçant des points.
Si vous avez oublié ce problème, consultez l'exemple 3.54. - Résoudre :\(2 x^{2}+3 x-2=0\).
Si vous avez oublié ce problème, consultez l'exemple 6.45. - Évaluez\(-\frac{b}{2 a}\) quand\(a=3\) et\(b=-6\).
Si vous avez oublié ce problème, consultez l'exemple 1.21.
Reconnaître le graphe d'une fonction quadratique
Auparavant, nous avons examiné très brièvement la fonction\(f(x)=x^{2}\), que nous avons appelée fonction carrée. C'est l'une des premières fonctions non linéaires que nous avons examinées. Nous allons maintenant représenter graphiquement les fonctions du formulaire\(f(x)=a x^{2}+b x+c\) si\(a \neq 0\). Nous appelons ce type de fonction une fonction quadratique.
Une fonction quadratique, où\(a, b\), et\(c\) sont des nombres réels et\(a≠0\), est une fonction de la forme
\(f(x)=a x^{2}+b x+c\)
Nous avons représenté graphiquement la fonction quadratique\(f(x)=x^{2}\) en traçant des points.
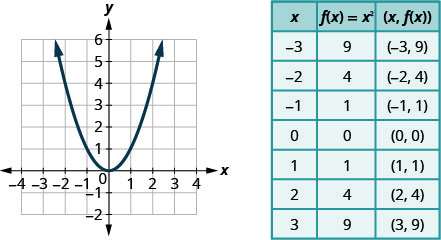
Chaque fonction quadratique possède un graphe qui ressemble à ceci. Nous appelons ce chiffre une parabole. Entraînons-nous à représenter graphiquement une parabole en traçant quelques points.
Graphique :\(f(x)=x^{2}-1\).
Solution :
Nous allons représenter graphiquement la fonction en traçant des points.
|
Choisissez des valeurs entières pour\(x\), |
 |
| Tracez les points, puis reliez-les à l'aide d'une courbe lisse. Le résultat sera le graphe de la fonction\(f(x)=x^{2}-1\). |
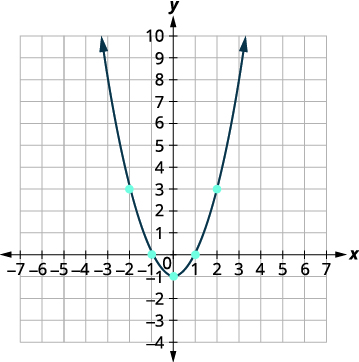 |
Graphe\(f(x)=-x^{2}\).
- Réponse
-
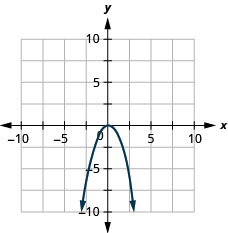
Graphe\(f(x)=x^{2}-1\).
- Réponse
-
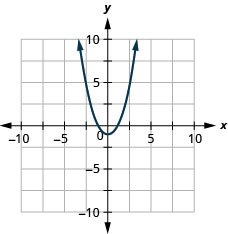
Tous les graphes des fonctions quadratiques de la forme\(f(x)=a x^{2}+b x+c\) sont des paraboles qui s'ouvrent vers le haut ou vers le bas. Voir la Figure 9.6.6
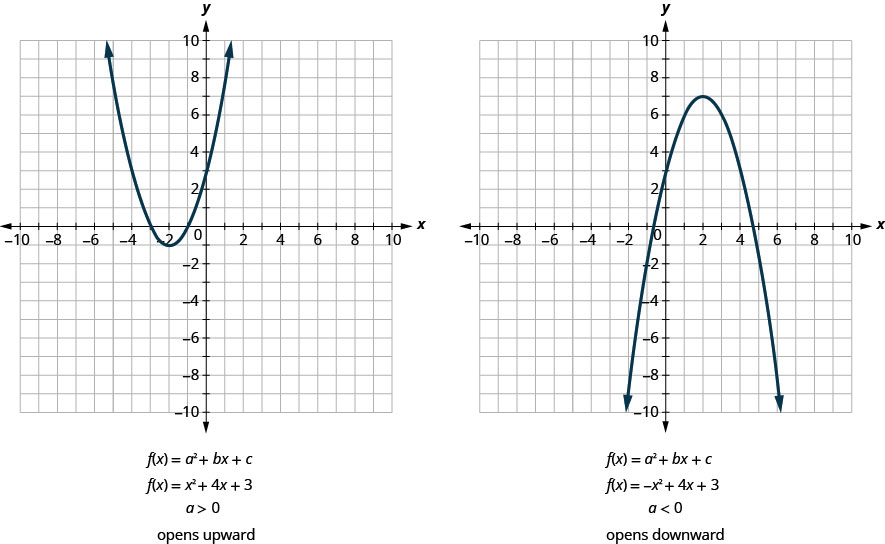
Notez que la seule différence entre les deux fonctions est le signe négatif avant le terme quadratique (\(x^{2}\)dans l'équation du graphique de la Figure 9.6.6). Lorsque le terme quadratique est positif, la parabole s'ouvre vers le haut, et lorsque le terme quadratique est négatif, la parabole s'ouvre vers le bas.
Orientation parabolique
Pour le graphe de la fonction quadratique\(f(x)=a x^{2}+b x+c\), si

Déterminez si chaque parabole s'ouvre vers le haut ou le bas :
- \(f(x)=-3 x^{2}+2 x-4\)
- \(f(x)=6 x^{2}+7 x-9\)
Solution :
a. Déterminez la valeur de\(a\).
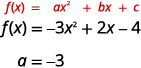
Comme la valeur\(a\) est négative, la parabole s'ouvrira vers le bas.
b. Déterminez la valeur de\(a\).
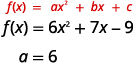
Comme le\(a\) est positif, la parabole s'ouvrira vers le haut.
Déterminez si le graphe de chaque fonction est une parabole qui s'ouvre vers le haut ou vers le bas :
- \(f(x)=2 x^{2}+5 x-2\)
- \(f(x)=-3 x^{2}-4 x+7\)
- Réponse
-
- en haut
- vers le bas
Déterminez si le graphe de chaque fonction est une parabole qui s'ouvre vers le haut ou vers le bas :
- \(f(x)=-2 x^{2}-2 x-3\)
- \(f(x)=5 x^{2}-2 x-1\)
- Réponse
-
- vers le bas
- en haut
Trouvez l'axe de symétrie et le sommet d'une parabole
Regardez à nouveau la Figure 9.6.10. Voyez-vous que nous pourrions plier chaque parabole en deux et qu'un côté se trouverait au-dessus de l'autre ? La « ligne de pliage » est une ligne de symétrie. Nous l'appelons l'axe de symétrie de la parabole.
Nous remontrons les deux mêmes graphes avec l'axe de symétrie.
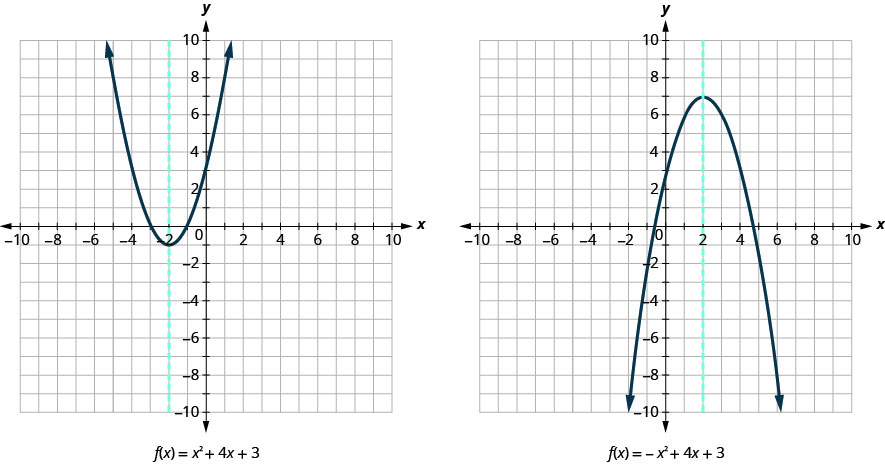
L'équation de l'axe de symétrie peut être dérivée à l'aide de la formule quadratique. Nous allons omettre la dérivation ici et passer directement à l'utilisation du résultat. L'équation de l'axe de symétrie du graphe de\(f(x)=a x^{2}+b x+c\) est\(x=-\frac{b}{2 a}\).
Donc, pour trouver l'équation de symétrie de chacune des paraboles que nous avons représentées ci-dessus, nous la remplacerons dans la formule\(x=-\frac{b}{2 a}\).
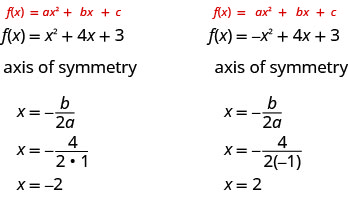
Notez que ce sont les équations des lignes bleues en pointillés sur les graphiques.
Le point de la parabole qui est le plus bas (la parabole s'ouvre) ou le plus haut (la parabole s'ouvre vers le bas) se trouve sur l'axe de symétrie. Ce point est appelé sommet de la parabole.
Nous pouvons facilement trouver les coordonnées du sommet, car nous savons qu'il se trouve sur l'axe de symétrie. Cela signifie que sa
\(x\) coordonnée est\(-\frac{b}{2 a}\). Pour trouver la\(y\) coordonnée du sommet, nous substituons la valeur de la\(x\) coordonnée -dans la fonction quadratique.
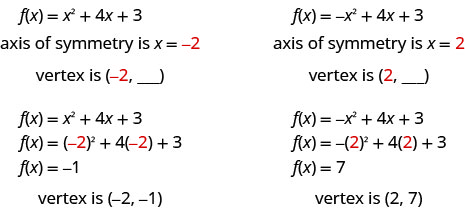
Axe de symétrie et sommet d'une parabole
Le graphique de la fonction\(f(x)=a x^{2}+b x+c\) est une parabole où :
- l'axe de symétrie est la ligne verticale\(x=-\frac{b}{2 a}\).
- le sommet est un point sur l'axe de symétrie, donc sa\(x\) coordonnée est\(-\frac{b}{2 a}\)
- la\(y\) coordonnée -du sommet est trouvée en la substituant\(x=-\frac{b}{2 a}\) dans l'équation quadratique.
Pour le graphique de la\(f(x)=3 x^{2}-6 x+2\) découverte :
- l'axe de symétrie
- le sommet
Solution :
un.
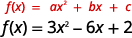 |
|
| L'axe de symétrie est la ligne verticale\(x=-\frac{b}{2 a}\). | |
| Substituez les valeurs\(a,b\) dans l'équation. | \(x=-\frac{-6}{2 \cdot 3}\) |
| Simplifiez. | \(x=1\) |
| L'axe de symétrie est la ligne\(x=1\). |
b.
| \(f(x)=3 x^{2}-6 x+2\) | |
| Le sommet est un point sur la ligne de symétrie, donc sa coordonnée en «\(x\) -coordonnée » le sera\(x=1\). Trouvez\(f(1)\). | 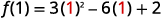 |
| Simplifiez. |  |
| Le résultat est la\(y\) coordonnée. | \(f(1)=-1\) |
| Le sommet est\((1,-1)\). |
Pour le graphique de la\(f(x)=2 x^{2}-8 x+1\) découverte :
- l'axe de symétrie
- le sommet
- Réponse
-
- \(x=2\)
- \((2,-7)\)
Pour le graphique de la\(f(x)=2 x^{2}-4 x-3\) découverte :
- l'axe de symétrie
- le sommet
- Réponse
-
- \(x=1\)
- \((1,-5)\)
Trouvez les points d'intersection d'une parabole
Lorsque nous avons représenté graphiquement des équations linéaires, nous avons souvent utilisé\(y\) les interceptions\(x\) - et - pour nous aider à tracer les lignes. La recherche des coordonnées des interceptions nous aidera également à tracer des paraboles.
N'oubliez pas qu'à l'\(y\)intersection, la valeur de\(x\) est nulle. Donc, pour trouver le\(y\) -intercept, nous le substituons\(x=0\) dans la fonction.
Trouvons les\(y\) -intercepts des deux paraboles présentées dans la Figure 9.6.20.
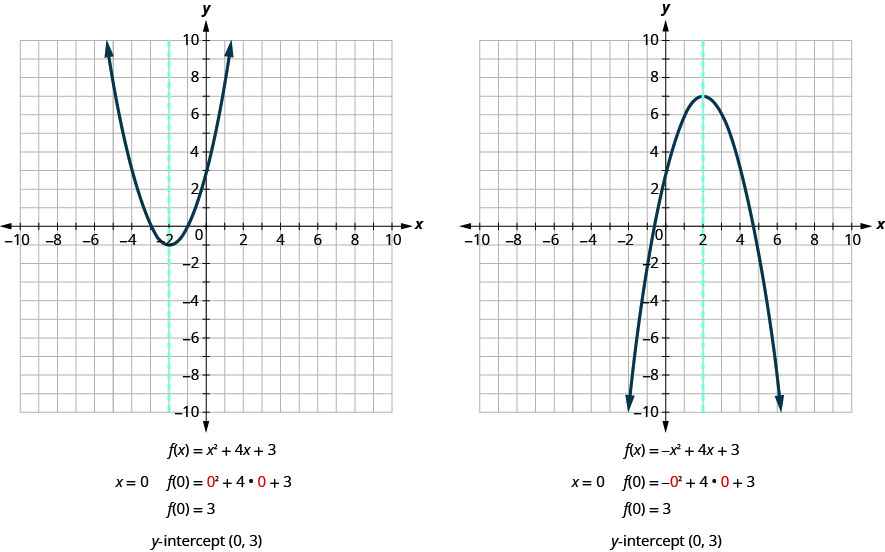
Un\(x\) -intercept se produit lorsque la valeur de\(f(x)\) est nulle. Pour trouver un\(x\) -intercept, on laisse\(f(x)=0\). En d'autres termes, nous devrons résoudre l'équation\(0=a x^{2}+b x+c\) pour\(x\).
\(\begin{aligned} f(x) &=a x^{2}+b x+c \\ 0 &=a x^{2}+b x+c \end{aligned}\)
Résoudre de telles équations quadratiques est exactement ce que nous avons fait plus tôt dans ce chapitre !
Nous pouvons maintenant trouver les\(x\) -intercepts des deux paraboles que nous avons examinées. Nous allons d'abord trouver les\(x\) -intercepts de la parabole dont la fonction est\(f(x)=x^{2}+4 x+3\).
| \(f(x)=x^{2}+4 x+3\) | |
| Laissez\(f(x)=0\). | \(\color{red}0\color{black}=x^{2}+4 x+3\) |
| Facteur. | \(0=(x+1)(x+3)\) |
| Utilisez la propriété Zero Product. | \(x+1=0 \quad x+3=0\) |
| Résoudre. | \(x=-1 \quad x=-3\) |
| Les\(x\) -intercepts sont\((-1,0)\) et\((-3,0)\). |
Nous allons maintenant trouver les\(x\) -intercepts de la parabole dont la fonction est\(f(x)=-x^{2}+4 x+3\).
| \(f(x)=-x^{2}+4 x+3\) | |
| Laissez\(f(x)=0\). | \(\color{red}0 \color{black}=-x^{2}+4 x+3\) |
| Ce quadratique ne prend pas en compte, nous utilisons donc la formule quadratique. | \(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| \(a=-1, b=4, c=3\) | \(x=\frac{-4 \pm \sqrt{4^{2}-4(-1)(3)}}{2(-1)}\) |
| Simplifiez. | \(x=\frac{-4 \pm \sqrt{28}}{-2}\) |
| \(x=\frac{-4 \pm 2 \sqrt{7}}{-2}\) | |
| \(x=\frac{-2(2 \pm \sqrt{7})}{-2}\) | |
| \(x=2 \pm \sqrt{7}\) | |
| Les\(x\) -intercepts sont\((2+\sqrt{7}, 0)\) et\((2-\sqrt{7}, 0)\). |
Nous utiliserons les approximations décimales des\(x\) -intercepts, afin de pouvoir localiser ces points sur le graphique,
\((2+\sqrt{7}, 0) \approx(4.6,0) \quad(2-\sqrt{7}, 0) \approx(-0.6,0)\)
Ces résultats sont-ils en accord avec nos graphiques ? Voir la Figure 9.6.34
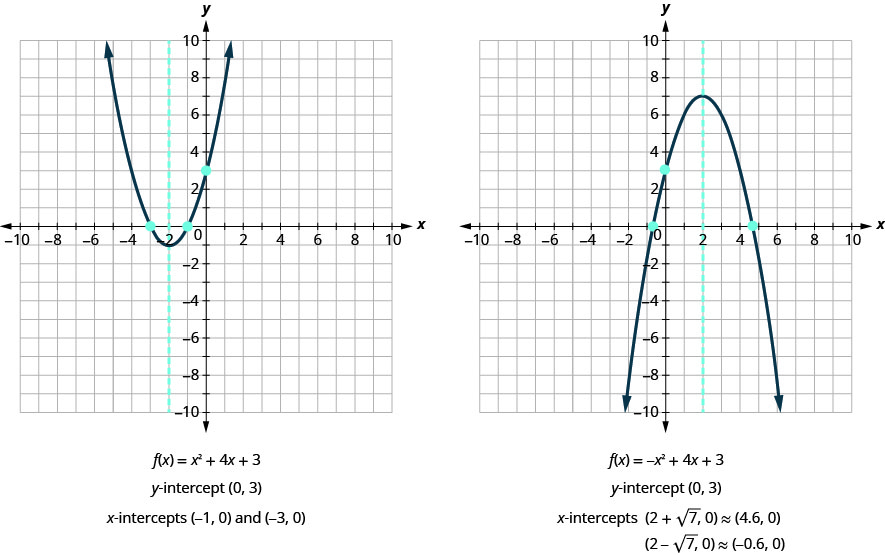
Trouvez les points d'intersection d'une parabole
Pour trouver les points d'intersection d'une parabole dont la fonction est\(f(x)=a x^{2}+b x+c\) :
\(y\)-intercepter
Laissez\(x=0\) et résolvez pour\(f(x)\).
\(x\)-intercepte
Laissez\(f(x)=0\) et résolvez pour\(x\)
Trouvez les points d'intersection de la parabole dont la fonction est\(f(x)=x^{2}-2 x-8\).
Solution :
| Pour trouver le\(y\) -intercept, laissez\(x=0\) et résolvez pour\(f(x)\). | \(f(x)=x^{2}-2 x-8\) |
| \(f(0)=\color{red}0\color{black}^{2}-2 \cdot \color{red}0 \color{black}-8\) | |
| \(f(0)=-8\) | |
| Quand\(x=0\), alors\(f(0)=-8\). Le\(y\) -intercept est le point\((0,-8)\). | |
| Pour trouver le\(x\) -intercept, laissez\(f(x)=0\) et résolvez pour\(x\). | \(f(x)=x^{2}-2 x-8\) |
| \(0=x^{2}-2 x-8\) | |
| Résolvez par factorisation. | \(0=(x-4)(x+2)\) |
| \(0=x-4 \quad 0=x+2\) | |
| \(4=x \quad-2=x\) | |
| Quand\(f(x)=0\), alors\(x=4\) ou\(x=-2\). Les\(x\) -intercepts sont les points\((4,0)\) et\((-2,0)\). |
Trouvez les points d'intersection de la parabole dont la fonction est\(f(x)=x^{2}+2 x-8\).
- Réponse
-
\(y\)-intercepter :\((0,-8) x\) -intercepte\((-4,0),(2,0)\)
Trouvez les points d'intersection de la parabole dont la fonction est\(f(x)=x^{2}-4 x-12\).
- Réponse
-
\(y\)-intercepter :\((0,-12) x\) -intercepte\((-2,0),(6,0)\)
Dans ce chapitre, nous avons résolu des équations quadratiques de la forme\(a x^{2}+b x+c=0\). Nous avons résolu pour\(x\) et les résultats ont été les solutions à l'équation.
Nous examinons maintenant les fonctions quadratiques de la forme\(f(x)=a x^{2}+b x+c\). Les graphes de ces fonctions sont des paraboles. Les\(x\) - interceptions des paraboles se produisent à l'endroit où\(f(x)=0\).
Par exemple :
Équation quadratique
\(\begin{aligned}x^{2}-2 x-15 & =0\quad \text{Let}\:f(x)=0 \\ (x-5)(x+3) &=0 \\ x-5=0\:\:x+3 & =0 \\ x=5\:\:\:x&=-3\end{aligned}\)
Fonction quadratique
\(\begin{aligned} f(x) &=x^{2}-2 x-15 \\ 0 &=x^{2}-2 x-15 \\ 0 &=(x-5)(x+3) \\ x-5 &=0 \quad x+3=0 \\ x &=5 \quad x=-3 \\(5,0) & \text { and }(-3,0) \\& x\text { -intercepts } \end{aligned}\)
Les solutions de la fonction quadratique sont les\(x\) valeurs des interceptions\(x\) -.
Plus tôt, nous avons vu que les équations quadratiques ont\(2, 1\), ou\(0\) des solutions. Les graphiques ci-dessous présentent des exemples de paraboles pour ces trois cas. Puisque les solutions des fonctions donnent les\(x\) -intercepts des graphes, le nombre de\(x\) -intercepts est identique au nombre de solutions.
Auparavant, nous utilisions le discriminant pour déterminer le nombre de solutions d'une fonction quadratique de la forme\(a x^{2}+b x+c=0\). Nous pouvons maintenant utiliser le discriminant pour nous dire combien de\(x\) -intercepts il y a sur le graphique.
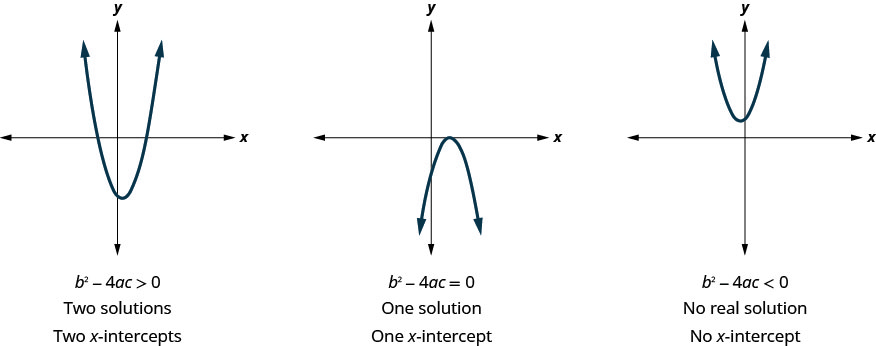
Avant de trouver les valeurs des\(x\) -intercepts, vous pouvez évaluer le discriminant afin de savoir à combien de solutions vous attendre.
Trouvez les points d'intersection de la parabole pour la fonction\(f(x)=5 x^{2}+x+4\).
Solution :
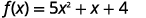 |
|
| Pour trouver le\(y\) -intercept, laissez\(x=0\) et résolvez pour\(f(x)\). |  |
 |
|
| Quand\(x=0\), alors\(f(0)=4\). Le\(y\) -intercept est le point\((0,4)\). | |
| Pour trouver le\(x\) -intercept, laissez\(f(x)=0\) et résolvez pour\(x\). | 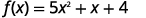 |
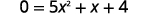 |
|
| Trouvez la valeur du discriminant pour prédire le nombre de solutions, qui est également le nombre de\(x\) -intercepts. | |
| \(\begin{array}{c}{b^{2}-4 a c} \\ {1^{2}-4 \cdot 5 \cdot 4} \\ {1-80} \\ {-79}\end{array}\) | |
|
La valeur du discriminant étant négative, il n'existe pas de véritable solution à l'équation. Il n'y a pas\(x\) de -intercepts. |
Trouvez les points d'intersection de la parabole dont la fonction est\(f(x)=3 x^{2}+4 x+4\).
- Réponse
-
\(y\)-intercept :\((0,4)\) non\(x\) -intercepter
Trouvez les points d'intersection de la parabole dont la fonction est\(f(x)=x^{2}-4 x-5\)
- Réponse
-
\(y\)-intercepter :\((0,-5)\)\(x\) -intercepte\((-1,0),(5,0)\)
Fonctions quadratiques graphiques à l'aide de propriétés
Nous avons maintenant toutes les pièces dont nous avons besoin pour représenter graphiquement une fonction quadratique. Nous avons juste besoin de les assembler. Dans l'exemple suivant, nous verrons comment procéder.
\(f(x)=x^{2}-6x+8\)Tracez un graphique en utilisant ses propriétés.
Solution :
| Étape 1 : Déterminez si la parabole s'ouvre vers le haut ou vers le bas. |
Regardez\(a\) dans l'équation\(f(x)=x^{2}-6x+8\) Puisque\(a\) c'est positif, la parabole s'ouvre vers le haut. |
\(f(x)=x^{2}-6x+8\) \(\color{red}{a=1, b=-6, c=8}\) La parabole s'ouvre vers le haut. |
| Étape 2 : Trouvez l'axe de symétrie |
\(f(x)=x^{2}-6x+8\) L'axe de symétrie est la ligne\(x=-\frac{b}{2 a}\). |
Axe de symétrie \(x=-\frac{b}{2 a}\) \(x=-\frac{(-6)}{2 \cdot 1}\) \(x=3\) L'axe de symétrie est la ligne\(x=3\). |
| Étape 3 : Trouvez le sommet | Le sommet se trouve sur l'axe de symétrie. \(x=3\)Substituez dans la fonction. |
Sommet \(f(x)=x^{2}-6x+8\) \(f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8\) \(f(3)=-1\) Le sommet est\((3,-1)\). |
| Étape 4 : Trouvez le\(y\) -intercept. Trouvez le point symétrique par rapport à l'\(y\)intersection -sur l'axe de symétrie. |
Nous trouvons\(f(0)\). Nous utilisons l'axe de symétrie pour trouver un point symétrique à l'\(y\)intersection. Le\(y\) -intercept correspond aux\(3\) unités situées à gauche de l'axe de symétrie,\(x=3\). Une\(3\) unité ponctuelle située à droite de l'axe de symétrie possède\(x=6\). |
\(y\)-intercepter \(f(x)=x^{2}-6 x+8\) \(f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8\) \(f(0)=8\) Le\(y\) -intercept est\((0,8)\). Point symétrique par rapport à\(y\) -intercept : Le fait est que\((6,8)\). |
| Étape 5 : Trouvez les\(x\) -intercepts. Trouvez des points supplémentaires si nécessaire. |
Nous résolvons\(f(x)=0\). Nous pouvons résoudre cette équation quadratique par factorisation. |
\(x\)-intercepte \(f(x)=x^{2}-6 x+8\) \(\color{red}{0}\color{black}{=}x^{2}-6x+8\) \(\color{red}{0}\color{black}{=}(x-2)(x-4)\) \(x=2 or x=4\) Les\(x\) -intercepts sont\((2,0)\) et\((4,0)\). |
| Étape 6 : Tracez la parabole. | Nous représentons graphiquement le sommet, les interceptions et le point symétriquement par\(y\) rapport à l'intersection. Nous relions ces\(5\) points pour esquisser la parabole. | .png) |
\(f(x)=x^{2}+2x-8\)Tracez un graphique en utilisant ses propriétés.
- Réponse
-
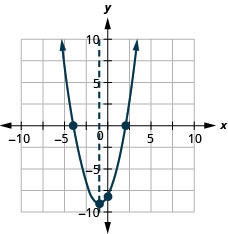
\(f(x)=x^{2}-8x+12\)Tracez un graphique en utilisant ses propriétés.
- Réponse
-
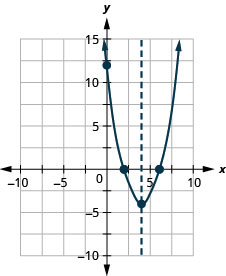
Nous listons les étapes à suivre pour représenter graphiquement une fonction quadratique ici.
Pour représenter graphiquement une fonction quadratique à l'aide de propriétés
- Détermine si la parabole s'ouvre vers le haut ou vers le bas.
- Trouvez l'équation de l'axe de symétrie.
- Trouve le sommet.
- Trouvez le\(y\) -intercept. Trouvez le point symétrique par rapport à l'\(y\)intersection -sur l'axe de symétrie.
- Trouvez les\(x\) -intercepts. Trouvez des points supplémentaires si nécessaire.
- Tracez la parabole.
Nous avons pu trouver les\(x\) -intercepts dans le dernier exemple en les factorisant. Nous trouvons les\(x\) -intercepts dans l'exemple suivant en les factorisant également.
\(f(x)=-x^{2}+6 x-9\)Tracez un graphique en utilisant ses propriétés.
Solution :
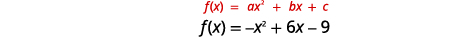 |
|
| Depuis lors\(a\)\(-1\), la parabole s'ouvre vers le bas. | |
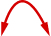 |
|
| Pour trouver l'équation de l'axe de symétrie, utilisez\(x=-\frac{b}{2 a}\). | \(x=-\frac{b}{2 a}\) |
| \(x=-\frac{6}{2(-1)}\) | |
| \(x=3\) | |
|
L'axe de symétrie est\(x=3\). Le sommet se trouve sur la ligne\(x=3\). |
|
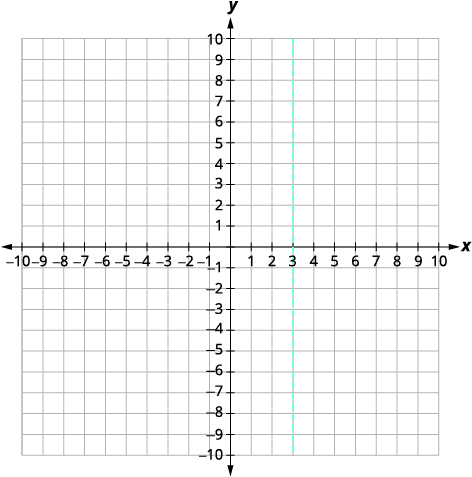 |
|
| Trouvez\(f(3)\). | \(f(x)=-x^{2}+6 x-9\) |
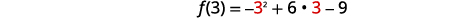 |
|
| \(f(3)=-9+18-9\) | |
| \(f(3)=0\) | |
| Le sommet est\((3,0)\). | |
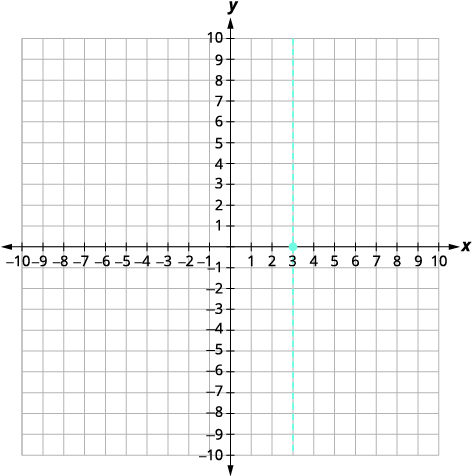 |
|
| Le\(y\) -intercept se produit lorsque\(x=0\). Trouvez\(f(0)\). | \(f(x)=-x^{2}+6 x-9\) |
| Substitut\(x=0\). | 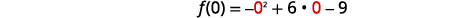 |
| Simplifiez. | \(f(0)=-9\) |
| Le point\((0,-9)\) se trouve à trois unités à gauche de la ligne de symétrie. Le point situé à trois unités à droite de la ligne de symétrie est\((6,-9)\). | 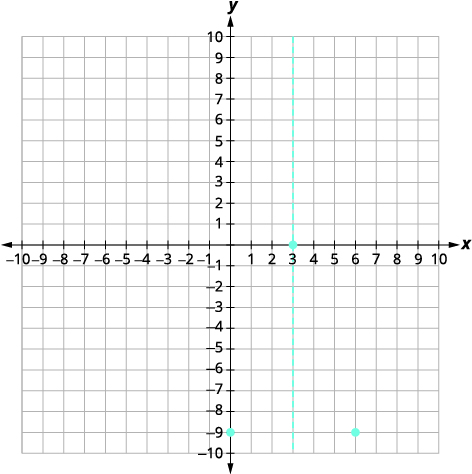 |
| Le point symétrique par rapport à l'\(y\)-intercept est\((6,-9)\) | |
| Le\(x\) -intercept se produit lorsque\(f(x)=0\). | 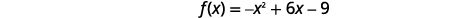 |
| Trouvez\(f(x)=0\). | 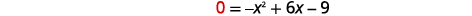 |
| Tenez compte du GCF. | 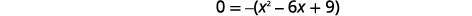 |
| Tenez compte du trinôme. | 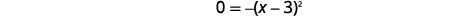 |
| Résolvez pour\(x\). | 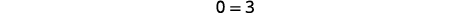 |
| Reliez les points pour représenter graphiquement la parabole. | 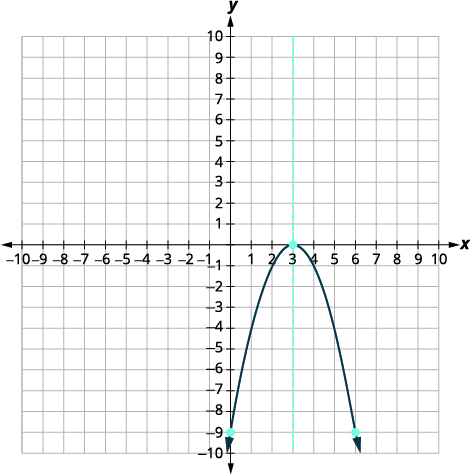 |
\(f(x)=3 x^{2}+12 x-12\)Tracez un graphique en utilisant ses propriétés.
- Réponse
-
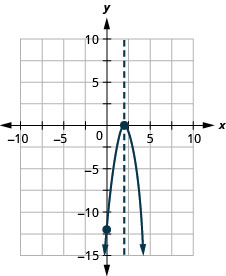
\(f(x)=4 x^{2}+24 x+36\)Tracez un graphique en utilisant ses propriétés.
- Réponse
-
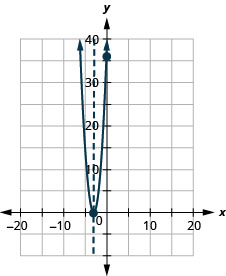
Pour le graphe de\(f(x)=-x^{2}+6 x-9\), le sommet et l'\(x\)intersection étaient le même point. Vous vous souvenez comment le discriminant détermine le nombre de solutions d'une équation quadratique ? Le discriminant de l'équation\(0=-x^{2}+6x-9\) est donc qu'\(0\)il n'y a qu'une seule solution. Cela signifie qu'il n'y a qu'une seule\(x\) intersection, et c'est le sommet de la parabole.
De combien\(x\) d'interceptions vous attendriez-vous à voir sur le graphique\(f(x)=x^{2}+4 x+5\) ?
\(f(x)=x^{2}+4 x+5\)Tracez un graphique en utilisant ses propriétés.
Solution :
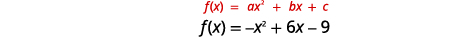 |
|
| Depuis lors\(a\)\(-1\), la parabole s'ouvre vers le bas. | |
 |
|
| Pour trouver l'équation de l'axe de symétrie, utilisez\(x=-\frac{b}{2 a}\). | 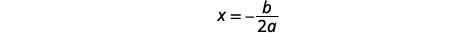 |
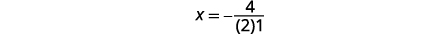 |
|
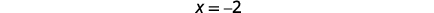 |
|
|
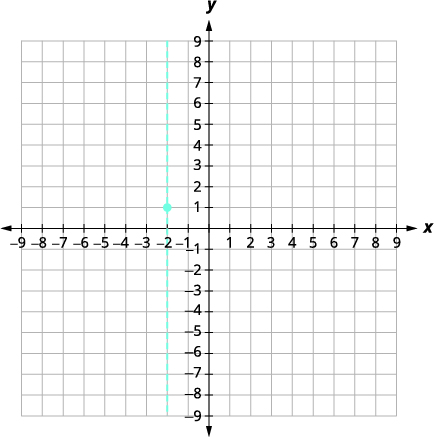
L'équation de l'axe de symétrie est \ (x=-2). |
|
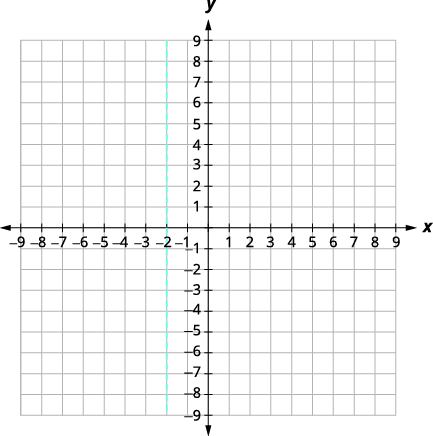 |
|
| Le sommet se trouve sur la ligne\(x=-2\). | |
| \(f(x)\)Trouve quand\(x=-2\). | 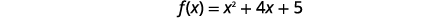 |
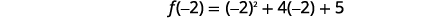 |
|
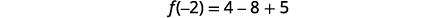 |
|
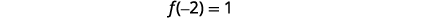 |
|
|
Le sommet est\((-2,1)\). |
|
 |
|
| Le\(y\) -intercept se produit lorsque\(x=0\). | 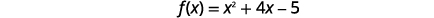 |
| Trouvez\(f(0)\). | 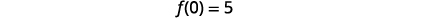 |
| Simplifiez. | 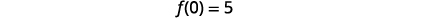 |
| Le\(y\) -intercept est\((0,5)\). | |
| Le point\((-4,5)\) se trouve à deux unités à gauche de la ligne de symétrie. Le point vers les unités à droite de la ligne de symétrie est \ (0,5) \. | 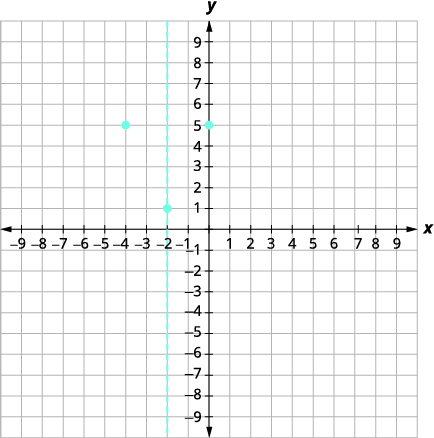 |
| Le point symétrique par rapport à l'\(y\)-intercept est\((-4,5)\). | |
| Le\(x\) -intercept se produit lorsque\(f(x)=0\). | 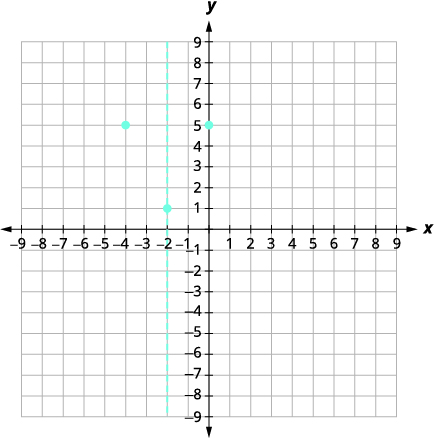 |
| Trouvez\(f(x)=0\). | 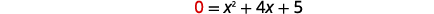 |
| Testez le discriminant. | |
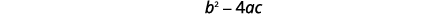 |
|
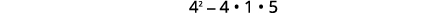 |
|
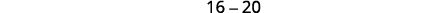 |
|
 |
|
| Puisque la valeur du discriminant est négative, il n'y a pas de solution réelle et donc pas\(x\) d'interception. | |
| Reliez les points pour représenter graphiquement la parabole. Vous pouvez choisir deux points supplémentaires pour une plus grande précision. | 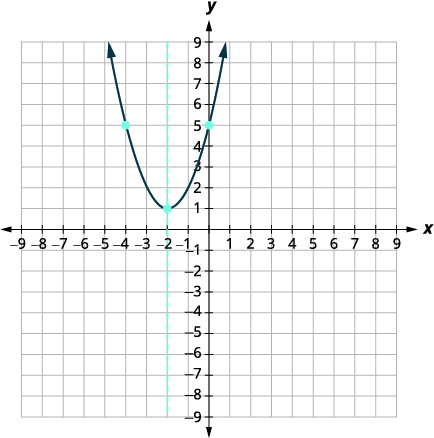 |
\(f(x)=x^{2}-2 x+3\)Tracez un graphique en utilisant ses propriétés.
- Réponse
-
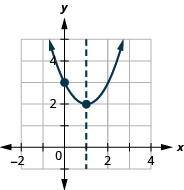
\(f(x)=-3x^{2}-6 x-4\)Tracez un graphique en utilisant ses propriétés.
- Réponse
-
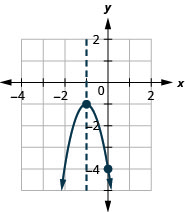
Trouver le\(y\) -intercept en trouvant\(f(0)\) est facile, n'est-ce pas ? Parfois, nous avons besoin d'utiliser la formule quadratique pour trouver les\(x\) -intercepts.
\(f(x)=2 x^{2}-4 x-3\)Tracez un graphique en utilisant ses propriétés.
Solution :
 |
|
|
Depuis lors\(a\)\(2\), la parabole s'ouvre vers le haut. |
 |
| Pour trouver l'équation de l'axe de symétrie, utilisez\(x=-\frac{b}{2 a}\). | \(x=-\frac{b}{2 a}\) |
| \(x=-\frac{-4}{2 \cdot 2}\) | |
| \(x=1\) | |
| L'équation de l'axe de symétrie est\(x=1\). | |
| Le sommet est sur la ligne\(x=1\). | \(f(x)=2 x^{2}-4 x-3\) |
| Trouvez\(f(1)\). |  |
| \(f(1)=2-4-3\) | |
| \ (\ f (1) =-5) | |
| Le sommet est\((1,-5)\). | |
| Le\(y\) -intercept se produit lorsque\(x=0\). | \(f(x)=2 x^{2}-4 x-3\) |
| Trouvez\(f(0)\). |  |
| Simplifiez. | \(f(0)=-3\) |
| Le\(y\) -intercept est\((0,-3)\). | |
| Le point\((0,-3)\) se trouve à une unité à gauche de la ligne de symétrie. | Le point symétrique par rapport à l'\(y\)-intercept est\((2,-3)\) |
| Le point situé à une unité à droite de la ligne de symétrie\((2,3)\). | |
| Le\(x\) -intercept se produit lorsque\(y=0\). | \(f(x)=2 x^{2}-4 x-3\) |
| Trouvez\(f(x)=0\). |  |
| Utilisez la formule quadratique. | \(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| Remplacez les valeurs de\(a,b\) et\(c\). | \(x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(2)(3)}}{2(2)}\) |
| Simplifiez. | \(x=\frac{-4 \pm \sqrt{16+24}}{4}\) |
| Simplifiez l'intérieur du radical. | \(x=\frac{4 \pm \sqrt{40}}{4}\) |
| Simplifiez le radical. | \(x=\frac{4 \pm 2 \sqrt{10}}{4}\) |
| Tenez compte du GCF. | \(x=\frac{2(2 \pm \sqrt{10})}{4}\) |
| Supprimez les facteurs courants. | \(x=\frac{2 \pm \sqrt{10}}{2}\) |
| Ecrivez comme deux équations. | \(x=\frac{2+\sqrt{10}}{2}, \quad x=\frac{2-\sqrt{10}}{2}\) |
| Approximation des valeurs. | \(x \approx 2.5, \quad x \approx-0.6\) |
| Les valeurs approximatives des\(x\) -intercepts sont\((2.5,0)\) et\((-0.6,0)\). | |
| Tracez la parabole en utilisant les points trouvés. | 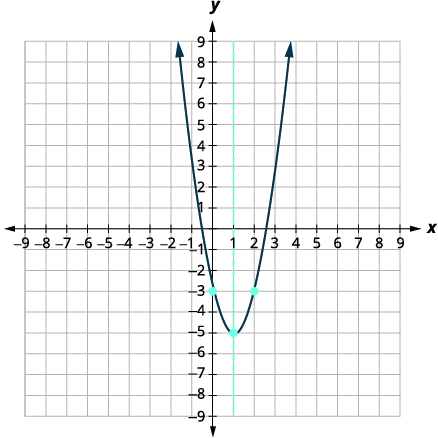 |
\(f(x)=5 x^{2}+10 x+3\)Tracez un graphique en utilisant ses propriétés.
- Réponse
-
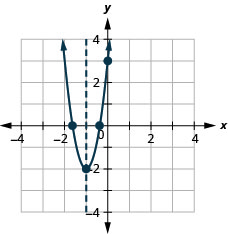
\(f(x)=-3 x^{2}-6 x+5\)Tracez un graphique en utilisant ses propriétés.
- Réponse
-
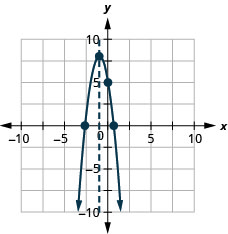
Résolvez les applications maximales et minimales
Le fait de savoir que le sommet d'une parabole est le point le plus bas ou le plus haut de la parabole nous permet de déterminer facilement la valeur minimale ou maximale d'une fonction quadratique. La coordonnée y du sommet est la valeur minimale d'une parabole qui s'ouvre vers le haut. Il s'agit de la valeur maximale d'une parabole qui s'ouvre vers le bas. Voir la Figure 9.6.124.
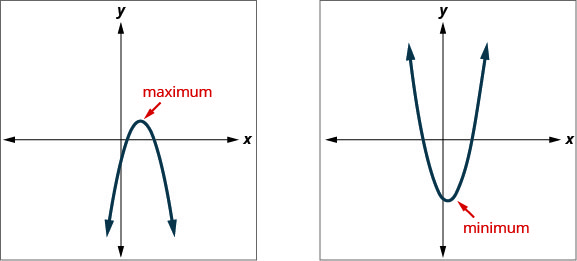
Valeurs minimales ou maximales d'une fonction quadratique
La coordonnée y du sommet du graphe d'une fonction quadratique est la
- valeur minimale de l'équation quadratique si la parabole s'ouvre vers le haut.
- valeur maximale de l'équation quadratique si la parabole s'ouvre vers le bas.
Détermine la valeur minimale ou maximale de la fonction quadratique\(f(x)=x^{2}+2 x-8\).
Solution :
| \(f(x)=x^{2}+2 x-8\) | |
| Puisque\(a\) c'est positif, la parabole s'ouvre vers le haut. L'équation quadratique a un minimum. | |
| Trouvez l'équation de l'axe de symétrie. | \(x=-\frac{b}{2 a}\) |
| \(x=-\frac{2}{2 \times 1}\) | |
| \(x=-1\) | |
| L'équation de l'axe de symétrie est\(x=-1\). | |
| Le sommet est sur la ligne\(x=-1\). | \(f(x)=x^{2}+2 x-8\) |
| Trouvez\(f(-1)\). | 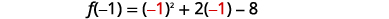 |
| \(f(-1)=1-2-8\) | |
| \(f(-1)=-9\) | |
| Le sommet est\((-1,-9)\). | |
| Comme la parabole possède un minimum, la\(y\) coordonnée du sommet est la\(y\) valeur minimale de l'équation quadratique. La valeur minimale du quadratique est\(-9\) et se produit quand\(x=-1\). | |
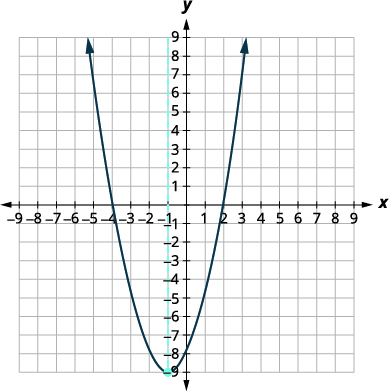 |
Montrez le graphique pour vérifier le résultat.
Détermine la valeur maximale ou minimale de la fonction quadratique\(f(x)=x^{2}-8 x+12\).
- Réponse
-
La valeur minimale de la fonction quadratique est\(−4\) et se produit quand\(x=4\).
Détermine la valeur maximale ou minimale de la fonction quadratique\(f(x)=-4 x^{2}+16 x-11\).
- Réponse
-
La valeur maximale de la fonction quadratique est\(5\) et se produit quand\(x=2\).
Nous avons utilisé la formule
\(h(t)=-16 t^{2}+v_{0} t+h_{0}\)
pour calculer la hauteur en pieds\(h\), d'un objet projeté vers le haut dans les airs à la vitesse initiale\(v_{0}\), après\(t\) quelques secondes.
Cette formule est une fonction quadratique, donc son graphe est une parabole. En résolvant les coordonnées du sommet\((t,h)\), nous pouvons déterminer le temps qu'il faudra à l'objet pour atteindre sa hauteur maximale. Ensuite, nous pouvons calculer la hauteur maximale.
L'équation quadratique\(h(t)=-16 t^{2}+176 t+4\) modélise la hauteur d'un ballon de volley-ball frappé droit vers le haut avec une vitesse en\(176\) pieds par seconde à partir d'une hauteur de\(4\) pieds.
- Combien de secondes faudra-t-il au volley-ball pour atteindre sa hauteur maximale ?
- Détermine la hauteur maximale du volley-ball.
Solution :
\(h(t)=-16 t^{2}+176 t+4\)
Puisque\(a\) c'est négatif, la parabole s'ouvre vers le bas. La fonction quadratique a un maximum.
a. Trouvez l'équation de l'axe de symétrie.
\(\begin{array}{l}{t=-\frac{b}{2 a}} \\ {t=-\frac{176}{2(-16)}} \\ {t=5.5}\end{array}\)
L'équation de l'axe de symétrie est\(t=5.5\).
Le sommet est sur la ligne\(t=5.5\).
Le maximum se produit en\(t=5.5\) secondes.
b. Trouvez\(h(5.5)\).
\(\begin{array}{l}{h(t)=-16 t^{2}+176 t+4} \\ {h(t)=-16(5.5)^{2}+176(5.5)+4}\end{array}\)
Utilisez une calculatrice pour simplifier.
\(h(t)=488\)
Le sommet est\((5.5,488)\).
Comme la parabole a un maximum, la\(h\) coordonnée du sommet est la valeur maximale de la fonction quadratique.
La valeur maximale de la quadratique est en\(488\) pieds et elle se produit en\(t=5.5\) secondes.
Après\(5.5\) quelques secondes, le volley-ball atteindra sa hauteur maximale de\(488\) pieds.
Résolvez en arrondissant les réponses au dixième le plus proche.
La fonction quadratique\(h(t)=-16 t^{2}+128 t+32\) est utilisée pour déterminer la hauteur d'une pierre projetée vers le haut à partir d'une hauteur de\(32\) pieds à une vitesse de pieds\(128\) par seconde. Combien de temps faudra-t-il pour que la pierre atteigne sa hauteur maximale ? Quelle est la hauteur maximale ?
- Réponse
-
Il faudra\(4\) quelques secondes pour que la pierre atteigne sa hauteur maximale de\(288\) pieds.
La trajectoire d'une fusée jouet lancée vers le haut depuis le sol à une vitesse de\(208\) pieds par seconde est modélisée par la fonction quadratique de\(h(t)=-16 t^{2}+208 t\). Quand la fusée atteindra-t-elle sa hauteur maximale ? Quelle sera la hauteur maximale ?
- Réponse
-
Il faudra\(6.5\) quelques secondes pour que la fusée atteigne sa hauteur maximale de\(676\) pieds.
Concepts clés
- Orientation parabolique
- Pour le graphe de la fonction quadratique\(f(x)=a x^{2}+b x+c\), si
- \(a>0\), la parabole s'ouvre vers le haut.
- \(a<0\), la parabole s'ouvre vers le bas.
- Pour le graphe de la fonction quadratique\(f(x)=a x^{2}+b x+c\), si
- Axe de symétrie et sommet d'une parabole Le graphe de la fonction\(f(x)=a x^{2}+b x+c\) est une parabole où :
- l'axe de symétrie est la ligne verticale\(x=-\frac{b}{2 a}\).
- le sommet est un point sur l'axe de symétrie, donc sa\(x\) coordonnée est\(-\frac{b}{2 a}\).
- la\(y\) coordonnée -du sommet est trouvée en la substituant\(x=-\frac{b}{2 a}\) dans l'équation quadratique.
- Trouvez les points d'intersection d'une parabole
- Pour trouver les points d'intersection d'une parabole dont la fonction est\(f(x)=a x^{2}+b x+c\) :
- \(y\)-intercepter
- Laissez\(x=0\) et résolvez pour\(f(x)\).
- \(x\)-intercepte
- Laissez\(f(x)=0\) et résolvez pour\(x\).
- \(y\)-intercepter
- Pour trouver les points d'intersection d'une parabole dont la fonction est\(f(x)=a x^{2}+b x+c\) :
- Comment représenter graphiquement une fonction quadratique à l'aide de propriétés.
- Détermine si la parabole s'ouvre vers le haut ou vers le bas.
- Trouvez l'équation de l'axe de symétrie.
- Trouve le sommet.
- Trouvez le\(y\) -intercept. Détermine le point symétrique par rapport à l'intersection y sur l'axe de symétrie.
- Trouvez les\(x\) -intercepts. Trouvez des points supplémentaires si nécessaire.
- Tracez la parabole.
- Valeurs minimales ou maximales d'une équation quadratique
- La\(y\) coordonnée -du sommet du graphe d'une équation quadratique est
- valeur minimale de l'équation quadratique si la parabole s'ouvre vers le haut.
- valeur maximale de l'équation quadratique si la parabole s'ouvre vers le bas.
Lexique
- fonction quadratique
- Une fonction quadratique\(a, b\), où et\(c\) sont des nombres réels et\(a≠0\), est fonction de la forme\(f(x)=ax^{2}+bx+c\).


