9.6 : Résoudre des applications d'équations quadratiques
- Page ID
- 194361
À la fin de cette section, vous serez en mesure de :
- Résolvez des applications modélisées par des équations quadratiques
Avant de commencer, répondez à ce questionnaire de préparation.
- La somme de deux nombres impairs consécutifs est\(−100\). Trouve les numéros.
Si vous avez oublié ce problème, consultez l'exemple 2.18. - Résoudre :\(\frac{2}{x+1}+\frac{1}{x-1}=\frac{1}{x^{2}-1}\).
Si vous avez oublié ce problème, consultez l'exemple 7.35. - Détermine la longueur de l'hypoténuse d'un triangle droit avec des jambes\(5\) en pouces et\(12\) en pouces.
Si vous avez oublié ce problème, consultez l'exemple 2.34.
Résolvez des applications modélisées par des équations quadratiques
Nous avons résolu certaines applications qui étaient modélisées par des équations quadratiques plus tôt, alors que la seule méthode que nous avions pour les résoudre était la factorisation. Maintenant que nous avons plus de méthodes pour résoudre des équations quadratiques, nous allons examiner de nouveau les applications.
Résumons d'abord les méthodes dont nous disposons maintenant pour résoudre des équations quadratiques.
Méthodes pour résoudre des équations quadratiques
- Affacturage
- Propriété Square Root
- Compléter le carré
- Formule quadratique
Au fur et à mesure que vous résolvez chaque équation, choisissez la méthode qui vous convient le mieux pour résoudre le problème. Pour rappel, nous copierons ici notre stratégie de résolution de problèmes habituelle afin de pouvoir suivre les étapes.
Utilisez une stratégie de résolution de problèmes
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
- Identifiez ce que nous recherchons.
- Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
- Traduisez en une équation. Il peut être utile de reformuler le problème en une phrase avec toutes les informations importantes. Traduisez ensuite la phrase anglaise en une équation algébrique.
- Résolvez l'équation en utilisant des techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
Nous avons résolu des applications numériques impliquant des entiers pairs et impairs consécutifs, en modélisant la situation à l'aide d'équations linéaires. N'oubliez pas que nous avons remarqué que chaque entier\(2\) pair est supérieur au nombre qui le précède. Si on appelle le premier\(n\), c'est le suivant\(n+2\). Le prochain serait\(n+2+2\) ou\(n+4\). Cela est également vrai lorsque nous utilisons des entiers impairs. Un ensemble d'entiers pairs et un ensemble d'entiers impairs sont présentés ci-dessous.
\(\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}\)
\(\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}\)
Certaines applications d'entiers consécutifs impairs ou pairs sont modélisées par des équations quadratiques. La notation ci-dessus vous sera utile lorsque vous nommerez les variables.
Le produit de deux entiers impairs consécutifs est\(195\). Trouve les nombres entiers.
Solution :
Étape 1 : Lisez le problème
Étape 2 : Identifiez ce que nous recherchons
Nous recherchons deux entiers impairs consécutifs.
Étape 3 : Nommez ce que nous recherchons.
Soit\(n=\) le premier entier impair.
\(n+2=\)le prochain entier impair.
Étape 4 : Traduisez en équation Exposez le problème en une phrase.
« Le produit de deux entiers impairs consécutifs est\(195\). » Le produit du premier entier impair et du second entier impair est\(195\).
Traduisez en une équation.
\(n(n+2)=195\)
Étape 5 : Résolvez l'équation Distribuez.
\(n^{2}+2 n=195\)
Écrivez l'équation sous forme standard.
\(n^{2}+2 n-195=0\)
Facteur.
\((n+15)(n-13)=0\)
Utilisez la propriété Zero Product.
\(n+15=0 \quad n-13=0\)
Résolvez chaque équation.
\(n=-15, \quad n=13\)
Ce sont des solutions\(n\) qui ont deux valeurs. Cela nous donnera deux paires d'entiers impairs consécutifs pour notre solution.
\(\begin{array}{cc}{\text { First odd integer } n=13} & {\text { First odd integer } n=-15} \\ {\text { next odd integer } n+2} & {\text { next odd integer } n+2} \\ {13+2} & {-15+2} \\ {15} & {-13}\end{array}\)
Étape 6 : Vérifiez la réponse
Ces paires fonctionnent-elles ? Sont-ils des entiers impairs consécutifs ?
\(\begin{aligned} 13,15 & \text { yes } \\-13,-15 & \text { yes } \end{aligned}\)
Est-ce leur produit\(195\) ?
\(\begin{aligned} 13 \cdot 15 &=195 &\text{yes} \\-13(-15) &=195 & \text { yes } \end{aligned}\)
Étape 7 : Répondez à la question
Deux entiers impairs consécutifs dont le produit\(195\) est\(13,15\) et\(-13,-15\).
Le produit de deux entiers impairs consécutifs est\(99\). Trouve les nombres entiers.
- Réponse
-
Les deux entiers impairs consécutifs dont le produit\(99\) est\(9, 11\), et\(−9, −11\).
Le produit de deux entiers pairs consécutifs est\(168\). Trouve les nombres entiers.
- Réponse
-
Les deux entiers pairs consécutifs dont le produit\(128\) est\(12, 14\) et\(−12, −14\).
Nous utiliserons la formule de l'aire d'un triangle pour résoudre l'exemple suivant.
Aire d'un triangle
Pour un triangle ayant une base et une hauteur\(h\), l'aire,\(A\), est donnée par la formule\(A=\frac{1}{2} b h\).\(b\)
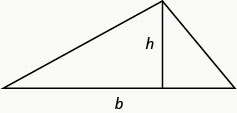
Rappelez-vous que lorsque nous résolvons des applications géométriques, il est utile de dessiner la figure.
Un architecte dessine l'entrée d'un restaurant. Elle veut placer une fenêtre triangulaire au-dessus de la porte. En raison de restrictions énergétiques, la fenêtre ne peut avoir qu'une surface de pieds\(120\) carrés et l'architecte souhaite que la base\(4\) mesure plus de deux fois la hauteur. Trouvez la base et la hauteur de la fenêtre.
Solution :
| Étape 1 : Lisez le problème Dessine une photo. | 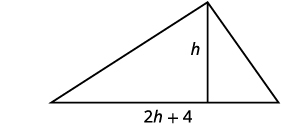 |
| Étape 2 : Identifiez ce que nous recherchons | Nous recherchons la base et la hauteur. |
| Étape 3 : Nommez ce que nous recherchons. |
Laissez\(h=\) la hauteur du triangle. \(2h+4=\)la base du triangle. |
|
Étape 4 : Traduisez en équation Nous connaissons la région. Écrivez la formule pour l'aire d'un triangle. |
\(A=\frac{1}{2} b h\) |
| Étape 5 : Résolvez l'équation Substituez les valeurs. | \(120=\frac{1}{2}(2 h+4) h\) |
| Distribuez. | \(120=h^{2}+2 h\) |
| Il s'agit d'une équation quadratique, réécrivez-la sous forme standard. | \(h^{2}+2 h-120=0\) |
| Facteur. | \((h-10)(h+12)=0\) |
| Utilisez la propriété Zero Product. | \(h-10=0 \quad h+12=0\) |
| Simplifiez. | \(h=10, \quad \cancel{h=-12}\) |
| Comme\(h\) c'est la hauteur d'une fenêtre, une valeur de\(h=-12\) n'a aucun sens. | |
| Hauteur du triangle\(h=10\). | |
|
La base du triangle\(2h+4\). \(2 \cdot 10+4\) \(24\) |
|
|
Étape 6 : Vérifiez la réponse Est-ce qu'un triangle avec hauteur\(10\) et base\(24\) a une surface\(120\) ? Oui. |
|
| Étape 7 : Répondez à la question | La hauteur de la fenêtre triangulaire est en\(10\) pieds et la base en\(24\) pieds. |
Déterminez la base et la hauteur d'un triangle dont la base mesure quatre pouces plus de six fois sa hauteur et dont la surface est de pouces\(456\) carrés.
- Réponse
-
La hauteur du triangle est\(12\) en pouces et la base en\(76\) pouces.
Si un triangle d'une superficie de pieds\(110\) carrés a une base de deux pieds de moins que deux fois la hauteur, quelles sont la longueur de sa base et sa hauteur ?
- Réponse
-
La hauteur du triangle est en\(11\) pieds et la base en\(20\) pieds.
Dans les deux exemples précédents, le nombre du radical dans la formule quadratique était un carré parfait et les solutions étaient donc des nombres rationnels. Si nous obtenons un nombre irrationnel comme solution à un problème d'application, nous utiliserons une calculatrice pour obtenir une valeur approximative.
Nous utiliserons la formule de l'aire d'un rectangle pour résoudre l'exemple suivant.
Aire d'un rectangle
Pour un rectangle de longueur et de largeur\(W\), la surface,\(A\), est donnée par la formule\(A=LW\).\(L\)
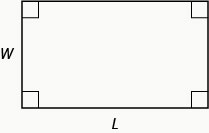
Mike veut mettre des pieds\(150\) carrés de gazon artificiel dans son jardin avant. Il s'agit de la superficie maximale de gazon artificiel autorisée par son association de propriétaires. Il veut avoir une surface de gazon rectangulaire d'une longueur d'un pied de moins que le\(3\) double de la largeur. Trouvez la longueur et la largeur. Arrondir au dixième de pied le plus proche.
Solution :
| Étape 1 : Lisez le problème Dessine une photo. |  |
| Étape 2 : Identifiez ce que nous recherchons | Nous recherchons la longueur et la largeur. |
| Étape 3 : Nommez ce que nous recherchons. |
Laissez\(w=\) la largeur du rectangle. \(3w-1=\)la longueur du rectangle |
| Étape 4 : Traduisez en équation Nous connaissons la région. Écrivez la formule pour l'aire d'un rectangle. |  |
| Étape 5 : Résolvez l'équation Substituez les valeurs. | 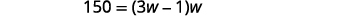 |
| Distribuez. | 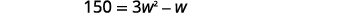 |
|
Il s'agit d'une équation quadratique ; réécrivez-la sous forme standard. Résolvez l'équation à l'aide de la formule quadratique. |
 |
| Identifiez les\(a,b,c\) valeurs. |  |
| Écrivez la formule quadratique. | 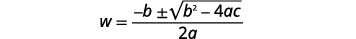 |
| Remplacez ensuite les valeurs de\(a,b,c\). | 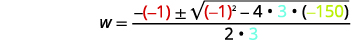 |
| Simplifiez. | 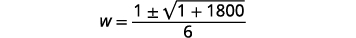
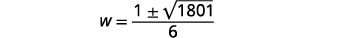
|
| Réécrivez pour afficher deux solutions. | 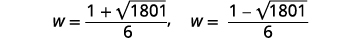 |
|
Faites une approximation des réponses à l'aide d'une calcul Nous éliminons la solution négative pour la largeur. |
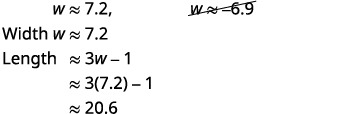 |
| Étape 6 : Vérifiez la réponse Assurez-vous que les réponses ont du sens. Comme les réponses sont approximatives, la zone ne sera pas exactement reproduite\(150\). | |
| Étape 7 : Répondez à la question | La largeur du rectangle est d'environ\(7.2\) pieds et la longueur est d'environ\(20.6\) pieds. |
La longueur d'un potager rectangulaire de pieds\(200\) carrés est inférieure de quatre pieds au double de la largeur. Détermine la longueur et la largeur du jardin, au dixième de pied près.
- Réponse
-
La longueur du jardin est d'environ\(18\) pieds et la largeur en\(11\) pieds.
Une nappe rectangulaire a une superficie de pieds\(80\) carrés. La largeur est inférieure de\(5\) pieds à la longueur. Quelles sont la longueur et la largeur de la nappe au dixième de pied près ?
- Réponse
-
La longueur de la nappe est d'environ 2\(11.8\) pieds et la largeur des\(6.8\) pieds.
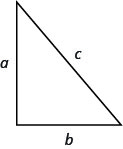
Le théorème de Pythagore donne la relation entre les jambes et l'hypoténuse d'un triangle droit. Nous utiliserons le théorème de Pythagore pour résoudre l'exemple suivant.
Théorème de Pythagore
Dans n'importe quel triangle droit, où\(a\) et\(b\) sont les longueurs des jambes, et\(c\) est la longueur de l'hypoténuse,\(a^{2}+b^{2}=c^{2}\).
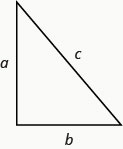
René met en place un éclairage de Noël. Il veut créer un « arbre » en forme de deux triangles droits, comme indiqué ci-dessous, et possède des guirlandes lumineuses de deux\(10\) pieds à utiliser sur les côtés. Il fixera les lumières au sommet d'un poteau et à deux piquets au sol. Il veut que la hauteur du mât soit la même que la distance entre la base du mât et chaque piquet. Quelle doit être la hauteur du mât ?
Solution :
| Étape 1 : Lisez le problème Dessine une photo. | 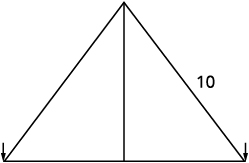 |
| Étape 2 : Identifiez ce que nous recherchons | Nous cherchons la hauteur du mât. |
| Étape 3 : Nommez ce que nous recherchons. |
La distance entre la base du mât et l'un ou l'autre piquet est la même que la hauteur du poteau. Laissez\(x=\) la hauteur du poteau. Chaque côté est un triangle droit. Nous dessinons une photo de l'un d'entre eux. 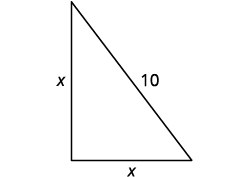
|
|
Étape 4 : Traduisez en équation Nous pouvons utiliser le théorème de Pythagore pour résoudre\(x\). |
\(a^{2}+b^{2}=c^{2}\) |
| Étape 5 : Résolvez l'équation Substitut. | \(x^{2}+x^{2}=10^{2}\) |
| Simplifiez. | \(2 x^{2}=100\) |
| Divisez par\(2\) pour isoler la variable. | \(\frac{2 x^{2}}{2}=\frac{100}{2}\) |
| Simplifiez. | \(x^{2}=50\) |
| Utilisez la propriété Square Root. | \(x=\pm \sqrt{50}\) |
| Simplifiez le radical. | \(x=\pm 5 \sqrt{2}\) |
| Réécrivez pour afficher deux solutions. | \(x=5 \sqrt{2}, \quad \cancel{x=-5 \sqrt{2}}\) |
| Si nous approximons ce nombre au dixième le plus proche avec une calculatrice, nous trouvons\(x≈7.1\). | |
| Étape 6 : Vérifiez la réponse Vérifiez vous-même le théorème de Pythagore. | |
| Étape 7 : Répondez à la question | Le mât doit mesurer environ un\(7.1\) pied de haut. |
Le soleil projette une ombre depuis un mât de drapeau. La hauteur du mât du drapeau est trois fois la longueur de son ombre. La distance entre l'extrémité de l'ombre et le sommet du mât du drapeau est de\(20\) pieds. Détermine la longueur de l'ombre et la longueur du mât du drapeau. Arrondir au dixième le plus proche.
- Réponse
-
La longueur de l'ombre du mât est d'environ\(6.3\) pieds et la hauteur du mât est de\(18.9\) pieds.
La distance entre les coins opposés d'un champ rectangulaire est supérieure de quatre à la largeur du champ. La longueur du champ est le double de sa largeur. Trouvez la distance entre les coins opposés. Arrondir au dixième le plus proche.
- Réponse
-
La distance entre les coins opposés est d'environ\(7.2\) pieds.
La hauteur d'un projectile tiré vers le haut depuis le sol est modélisée par une équation quadratique. La vitesse initiale,\(v_{0}\), propulse l'objet vers le haut jusqu'à ce que la gravité fasse retomber l'objet.
La hauteur en pieds\(h\), d'un objet projeté vers le haut dans les airs à la vitesse initiale\(v_{0}\), après\(t\) quelques secondes, est donnée par la formule
\(h=-16 t^{2}+v_{0} t\)
Nous pouvons utiliser cette formule pour déterminer combien de secondes il faudra pour qu'un feu d'artifice atteigne une hauteur spécifique.
Un feu d'artifice est tiré vers le haut avec une vitesse initiale en\(130\) pieds par seconde. Combien de secondes faudra-t-il pour atteindre une hauteur de\(260\) pieds ? Arrondir au dixième de seconde le plus proche.
Solution :
| Étape 1 : Lisez le problème | |
| Étape 2 : Identifiez ce que nous recherchons | Nous cherchons le nombre de secondes, qui est le temps. |
| Étape 3 : Nommez ce que nous recherchons. | Laissez\(t=\) le nombre de secondes. |
| Étape 4 : Traduisez en équation Utilisez la formule. | 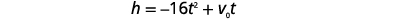 |
| Étape 5 : Résolvez l'équation Nous savons que la vitesse\(v_{0}\) est de\(130\) pieds par seconde. La hauteur est en\(260\) pieds. Remplacez les valeurs. | 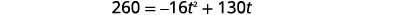 |
| Il s'agit d'une équation quadratique, réécrivez-la sous forme standard. Résolvez l'équation à l'aide de la formule quadratique. |  |
| Identifiez les valeurs de\(a, b, c\). |  |
| Écrivez la formule quadratique. | 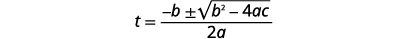 |
| Remplacez ensuite les valeurs de\(a,b,c\). | 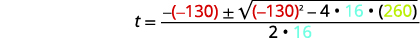 |
| Simplifiez. | 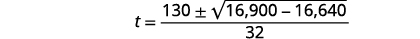
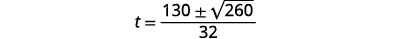
|
| Réécrivez pour afficher deux solutions. | 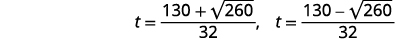 |
| Approximation de la réponse à l'aide d'une |  |
| Étape 6 : Vérifiez la réponse Le chèque est laissé à vous. | |
| Étape 7 : Répondez à la question | Le feu d'artifice montera puis retombera. Au fur et à mesure que le feu d'artifice monte, il atteindra\(260\) les pieds après environ\(3.6\) quelques secondes. Il passera également cette hauteur en descendant en\(4.6\) quelques secondes. |
Une flèche est projetée du sol dans les airs à une vitesse initiale de\(108\) pieds/s. Utilisez la formule\(h=-16 t^{2}+v_{0} t\) pour déterminer à quel moment la flèche se trouvera à\(180\) quelques pieds du sol. Environ le dixième le plus proche.
- Réponse
-
La flèche atteindra les\(180\) pieds en remontant au bout de\(3\) quelques secondes et de nouveau en descendant au bout de\(3.8\) quelques secondes environ.
Un homme lance une balle en l'air à une vitesse de\(96\) pieds/s. Utilisez la formule\(h=-16 t^{2}+v_{0} t\) pour déterminer à quel moment la hauteur de la balle sera de\(48\) pieds. Arrondir au dixième le plus proche.
- Réponse
-
La balle atteindra les\(48\) pieds en remontant au bout d'une\(.6\) seconde environ et de nouveau en descendant au bout de\(5.4\) quelques secondes environ.
Nous avons résolu les problèmes de mouvement uniforme en utilisant la formule\(D=rt\) des chapitres précédents. Nous avons utilisé un tableau comme celui ci-dessous pour organiser les informations et nous amener à l'équation.

La formule\(D=rt\) suppose que nous les connaissons\(r\)\(t\) et que nous les utilisons pour les trouver\(D\). Si nous savons\(D\) \(r\)et avons besoin de trouver\(t\), nous résoudrons l'équation pour\(t\) obtenir la formule\(t=\frac{D}{r}\).
Certains problèmes de mouvement uniforme sont également modélisés par des équations quadratiques.
Le professeur Smith vient de rentrer d'une conférence qui s'est tenue à des\(2,000\) kilomètres à l'est de chez lui. Le temps total qu'il a passé à bord de l'avion pour l'aller-retour était de\(9\) plusieurs heures. Si l'avion volait à une vitesse de\(450\) miles par heure, quelle était la vitesse du jet stream ?
Solution :
Il s'agit d'une situation de mouvement uniforme. Un diagramme nous aidera à visualiser la situation.

Nous remplissons le tableau pour organiser les informations.
Nous cherchons la vitesse du courant-jet. Laissez\(r=\) la vitesse du jet stream.
Lorsque l'avion vole avec le vent, le vent augmente sa vitesse et donc la vitesse\(450 + r\).
Lorsque l'avion vole contre le vent, le vent diminue sa vitesse et la vitesse diminue\(450 − r\).
| Inscrivez les tarifs. Inscrivez les distances. Depuis\(D=r⋅t\), nous résolvons \(t\) et obtenons\(t=\frac{D}{r}\). Nous divisons la distance par le taux de chaque ligne et plaçons l'expression dans la colonne temporelle. |
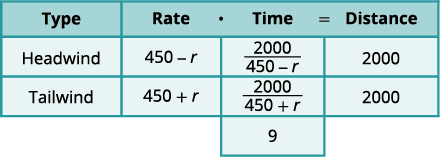 |
| Nous savons que les temps s'\(9\) additionnent et nous écrivons donc notre équation. |
\(\frac{2000}{450-r}+\frac{2000}{450+r}=9\) |
| Nous multiplions les deux côtés par l'écran LCD. | \((450-r)(450+r)\left(\frac{2000}{450-r}+\frac{2000}{450+r}\right)=9(450-r)(450+r)\) |
| Simplifiez. | \(2000(450+r)+2000(450-r)=9(450-r)(450+r)\) |
| Tenez compte du\(2,000\). | \(2000(450+r+450-r)=9\left(450^{2}-r^{2}\right)\) |
| Résoudre. | \(2000(900)=9\left(450^{2}-r^{2}\right)\) |
| Divisez par\(9\). | \(2000(100)=450^{2}-r^{2}\) |
| Simplifiez. |
\(\begin{aligned}200000&=202500-r^{2} \\ -2500&=-r^{2}\\ 50&=r\end{aligned}\)\ La vitesse du courant-jet est de\(50\) mph. |
|
Vérifiez : Est-ce que\(50\) mph est une vitesse raisonnable pour le jet stream ? Oui. Si l'avion roule à\(450\) mph et que le vent souffle à\(50\) mph, Vent arrière \(450+50=500 \mathrm{mph} \quad \frac{2000}{500}=4\)heures Vent de face \(450-50=400 \mathrm{mph} \quad \frac{2000}{400}=5\)heures Les temps s'\(9\)additionnent aux heures, donc ça vérifie. |
La vitesse du courant-jet était de\(50\) mi/h.
MaryAnne vient de rentrer d'une visite chez ses petits-enfants dans l'est du pays. Le voyage s'est fait\(2400\) à des kilomètres de son domicile et le temps total qu'elle a passé dans l'avion pour l'aller-retour était de\(10\) plusieurs heures. Si l'avion volait à une vitesse de\(500\) miles par heure, quelle était la vitesse du jet stream ?
- Réponse
-
La vitesse du courant-jet était de\(100\) mi/h.
Gerry vient de rentrer d'un voyage de fond. Le voyage s'est fait à des\(3000\) kilomètres de son domicile et il a passé au total des\(11\) heures dans l'avion pour l'aller-retour. Si l'avion volait à une vitesse de\(550\) miles par heure, quelle était la vitesse du jet stream ?
- Réponse
-
La vitesse du courant-jet était de\(50\) mi/h.
Les applications de travail peuvent également être modélisées par des équations quadratiques. Nous allons les configurer en utilisant les mêmes méthodes que celles que nous avons utilisées pour les résoudre avec des équations rationnelles. Nous allons maintenant utiliser un scénario similaire.
Le magazine hebdomadaire à potins raconte une grande histoire sur l'élection présidentielle et le rédacteur souhaite que le magazine soit imprimé le plus rapidement possible. Elle a demandé à l'imprimeur de faire fonctionner une presse supplémentaire pour que l'impression soit effectuée plus rapidement. Appuyez sur #1 prend des\(12\) heures de plus que sur Appuyez sur #2 pour effectuer le travail et lorsque les deux presses fonctionnent, elles peuvent imprimer le travail en\(8\) quelques heures. Combien de temps faut-il pour que chaque presse imprime le travail seule ?
Solution :
Il s'agit d'un problème de travail. Un tableau nous aidera à organiser l'information.
Nous cherchons le nombre d'heures qu'il faudrait à chaque presse séparément pour terminer le travail.
| Indiquez\(x=\) le nombre d'heures pendant lesquelles Appuyez sur #2 pour terminer le travail. Entrez les heures par tâche pour Appuyez sur #1, Appuyez sur #2 et quand ils travaillent ensemble. |
 |
| La partie terminée en appuyant sur #1 plus la partie terminée en appuyant sur #2 est égale à la quantité terminée ensemble. Traduisez en une équation. |
 |
| Résoudre. | 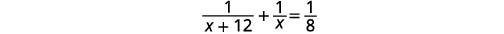 |
| Multipliez par l'écran LCD, 8\(x(x+12)\). | 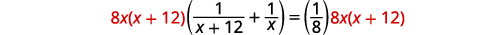 |
| Simplifiez. | 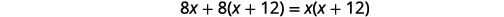
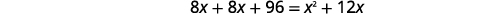

|
| Résoudre. | 
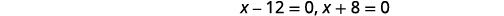

|
| Comme l'idée d'heures négatives n'a aucun sens, nous utilisons les valeurs\(x=12\). | 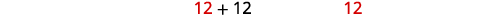
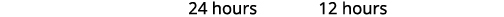
|
| Écrivez notre réponse à la phrase. | Appuyez sur #1 prendrait des\(24\) heures et sur Appuyer sur #2 prendrait des\(12\) heures pour faire le travail seul. |
Le magazine d'information hebdomadaire publie un article important en nommant la personnalité de l'année et le rédacteur souhaite que le magazine soit imprimé le plus rapidement possible. Elle a demandé à l'imprimeur de faire fonctionner une presse supplémentaire pour que l'impression soit effectuée plus rapidement. Appuyez sur #1 prend des\(6\) heures de plus que sur Appuyez sur #2 pour effectuer le travail et lorsque les deux presses fonctionnent, elles peuvent imprimer le travail en\(4\) quelques heures. Combien de temps faut-il pour que chaque presse imprime le travail seule ?
- Réponse
-
Appuyez sur #1 prendrait des\(12\) heures, et Appuyez sur #2 prendrait des\(6\) heures pour faire le travail seul.
Erlinda organise une fête et veut remplir son bain à remous. Si elle n'utilise que le tuyau rouge, cela prend des\(3\) heures de plus que si elle utilise uniquement le tuyau vert. Si elle utilise les deux tuyaux ensemble, le spa se remplit en\(2\) quelques heures. Combien de temps faut-il pour que chaque tuyau remplisse le spa ?
- Réponse
-
Le tuyau rouge prend des\(6\) heures et le tuyau vert prend des\(3\) heures seul.
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre des applications modélisées par des équations quadratiques.
Concepts clés
- Méthodes pour résoudre des équations quadratiques
- Affacturage
- Propriété Square Root
- Compléter le carré
- Formule quadratique
- Comment utiliser une stratégie de résolution de problèmes.
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
- Identifiez ce que nous recherchons.
- Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
- Traduisez en une équation. Il peut être utile de reformuler le problème en une phrase avec toutes les informations importantes. Traduisez ensuite la phrase anglaise en une équation d'algèbre.
- Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
- Aire d'un triangle
- Pour un triangle ayant une base et une hauteur\(h\), l'aire,\(A\), est donnée par la formule\(A=\frac{1}{2}bh\).\(b\)
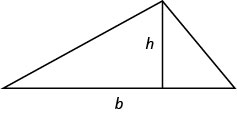
- Aire d'un rectangle
- Pour un rectangle de longueur et de largeur\(W\), la surface,\(A\), est donnée par la formule\(A=LW\).\(L\)
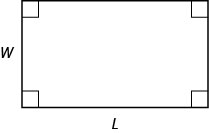
- Théorème de Pythagore
- Dans n'importe quel triangle droit, où\(a\) et\(b\) sont les longueurs des jambes, et\(c\) est la longueur de l'hypoténuse,\(a^{2}+b^{2}=c^{2}\).
- Mouvement du projectile
- La hauteur en pieds\(h\), d'un objet projeté vers le haut dans les airs à la vitesse initiale\(v_{0}\), après\(t\) quelques secondes est donnée par la formule\(h=-16 t^{2}+v_{0} t\).


