9.5 : Résoudre des équations quadratiques sous forme quadratique
- Page ID
- 194344
À la fin de cette section, vous serez en mesure de :
- Résolvez des équations sous forme quadratique
... répondez à ce questionnaire de préparation.
- Facteur par substitution :\(y^{4}-y^{2}-20\).
- Facteur par substitution :\((y-4)^{2}+8(y-4)+15\).
- SIMPLIFIER
- \(x^{\frac{1}{2}} \cdot x^{\frac{1}{4}}\)
- \(\left(x^{\frac{1}{3}}\right)^{2}\)
- \(\left(x^{-1}\right)^{2}\)
Résoudre des équations sous forme quadratique
Parfois, lorsque nous avons pris en compte les trinômes, le trinôme ne semblait pas être dans la\(ax^{2}+bx+c\) forme. Nous avons donc pris en compte par substitution, ce qui nous a permis de l'adapter à la\(ax^{2}+bx+c\) forme. Nous avons utilisé la norme\(u\) pour la substitution.
Pour factoriser l'expression\(x^{4}-4 x^{2}-5\), nous avons remarqué que la partie variable du terme moyen est\(x^{2}\) et que son carré est la partie variable du premier terme.\(x^{4}\) (Nous savons\(\left(x^{2}\right)^{2}=x^{4}\).) Nous avons donc laissé\(u=x^{2}\) et pris en compte.
| \(x^{4}-4 x^{2}-5\) | |
| \(\left(\color{red}x^2 \color{black} \right)^{2}-4\left( \color{red}x^{2} \color{black}\right)-5\) | |
| Laisser\(u=x^{2}\) et remplacer. | \(\color{red}u \color{black}^{2}-4 \color{red}u \color{black}-5\) |
| Tenez compte du trinôme. | \((u+1)(u-5)\) |
| Remplacez\(u\) par\(x^{2}\). | \(\left( \color{red}x^{2} \color{black} + 1\right)\left( \color{red}x^2 \color{black}-5\right)\) |
De même, il arrive qu'une équation ne soit pas dans la\(ax^{2}+bx+c=0\) forme mais ressemble beaucoup à une équation quadratique. Ensuite, nous pouvons souvent effectuer une substitution réfléchie qui nous permettra de l'adapter à la\(ax^{2}+bx+c=0\) forme. Si nous pouvons l'adapter à la forme, nous pouvons ensuite utiliser toutes nos méthodes pour résoudre des équations quadratiques.
Notez que dans l'équation quadratique\(ax^{2}+bx+c=0\), le terme moyen possède une variable et que son carré est la partie variable du premier terme.\(x\)\(x^{2}\) Recherchez cette relation lorsque vous essayez de trouver une substitution.
Encore une fois, nous utiliserons la norme\(u\) pour effectuer une substitution qui mettra l'équation sous forme quadratique. Si la substitution nous donne une équation de la forme\(ax^{2}+bx+c=0\), nous disons que l'équation d'origine était de forme quadratique.
L'exemple suivant montre les étapes de résolution d'une équation sous forme quadratique.
Résoudre :\(6 x^{4}-7 x^{2}+2=0\)
Solution :
| Étape 1 : Identifiez une substitution qui mettra l'équation sous forme quadratique. | Depuis\(\left(x^{2}\right)^{2}=x^{4}\), on a laissé\(u=x^{2}\). | \(6 x^{4}-7 x^{2}+2=0\) |
| Étape 2 : Réécrivez l'équation avec la substitution pour la mettre sous forme quadratique. |
Réécrivez pour préparer la substitution. Substitut\(u=x^{2}\). |
\(\begin{aligned}6\color{black}{\left(\color{red}{x^{2}}\right)}^{2}-7\color{red}{ x^{2}}\color{black}{+}2&=0 \\ \color{black}{6 \color{red}{u}^{2}}-7 \color{red}{u}\color{black}{+}2&=0\end{aligned}\) |
| Étape 3 : Résolvez l'équation quadratique pour\(u\). |
Nous pouvons le résoudre en affacturant. Utilisez la propriété Zero Product. |
\(\begin{aligned}(2 u-1)(3 u-2) &=0 \\ 2 u-1=0, 3 u-2&=0 \\ 2 u =1,3 u&=2 \\ u =\frac{1}{2} u&=\frac{2}{3} \end{aligned}\) |
| Étape 4 : Remplacez la variable d'origine dans les résultats en utilisant la substitution. | Remplacez\(u\) par\(x^{2}\). | \(x^{2}=\frac{1}{2} \quad x^{2}=\frac{2}{3}\) |
| Étape 5 : Résolvez la variable d'origine. | Résolvez pour\(x\), en utilisant la propriété Square Root. |
\(\begin{array}{ll}{x=\pm \sqrt{\frac{1}{2}}} & {x=\pm \sqrt{\frac{2}{3}}} \\ {x=\pm \frac{\sqrt{2}}{2}} & {x=\pm \frac{\sqrt{6}}{3}}\end{array}\) Il existe quatre solutions. \(\begin{array}{ll}{x=\frac{\sqrt{2}}{2}} & {x=\frac{\sqrt{6}}{3}} \\ {x=-\frac{\sqrt{2}}{2}} & {x=-\frac{\sqrt{6}}{3}}\end{array}\) |
| Étape 6 : Vérifiez les solutions | Vérifiez les quatre solutions. Nous vous montrerons un chèque ici. |
\(\begin{aligned}x&=\frac{\sqrt{2}}{2} \\ 6 x^{4}-7 x^{2}+2&=0 \\ 6\left(\frac{\sqrt{2}}{2}\right)^{4}-7\left(\frac{\sqrt{2}}{2}\right)^{2}+2 &\stackrel{?}{=} 0\\ 6\left(\frac{4}{16} \right)-7\left(\frac{2}{4} \right)^{2}+2&\stackrel{?}{=}0 \\ \frac{3}{2}-\frac{7}{2}+\frac{4}{2}&\stackrel{?}{=}0 \\ 0&=0 \end{aligned}\) Nous vous laissons les autres chèques ! |
Résoudre :\(x^{4}-6 x^{2}+8=0\).
- Réponse
-
\(x=\sqrt{2}, x=-\sqrt{2}, x=2, x=-2\)
Résoudre :\(x^{4}-11 x^{2}+28=0\).
- Réponse
-
\(x=\sqrt{7}, x=-\sqrt{7}, x=2, x=-2\)
Nous résumons les étapes pour résoudre une équation sous forme quadratique.
- Identifiez une substitution qui mettra l'équation sous forme quadratique.
- Réécrivez l'équation avec la substitution pour la mettre sous forme quadratique.
- Résolvez l'équation quadratique pour\(u\).
- Remplacez la variable d'origine dans les résultats en utilisant la substitution.
- Résolvez pour la variable d'origine.
- Vérifiez les solutions.
Dans l'exemple suivant, le binôme du moyen terme\((x-2)\) est mis au carré au premier terme. Si nous le laissons\(u=x-2\) et le remplaçons, notre trinôme sera en\(a x^{2}+b x+c\) forme.
Résoudre :\((x-2)^{2}+7(x-2)+12=0\).
Solution :
| \((x-2)^{2}+7(x-2)+12=0\) | |
| Préparez-vous à la substitution. | \(\color{red}(x-2)\color{black}^{2}+7\color{red}(x-2) \color{black} +12=0\) |
| Laisser\(u=x-2\) et remplacer. | \(\color{red}u^{\color{black}2} \color{black}+ 7 \color{red}u \color{black}+12=0\) |
| Résolvez par factorisation. |
\((u+3)(u+4)=0\) \ (\ begin {rassemblé} |
|
Remplacez\(u\) par\(x-2\). |
\(x-2=-3, \quad x-2=-4\) |
|
Résolvez pour\(x\). |
\(x=-1, \quad x=-2\) |
|
Vérifiez : 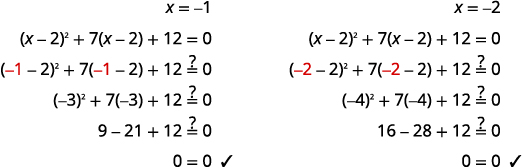
|
Résoudre :\((x-5)^{2}+6(x-5)+8=0\).
- Réponse
-
\(x=3, x=1\)
Résoudre :\((y-4)^{2}+8(y-4)+15=0\).
- Réponse
-
\(y=-1, y=1\)
Dans l'exemple suivant, nous le remarquons\((\sqrt{x})^{2}=x\). N'oubliez pas non plus que lorsque nous mettons les deux côtés d'une équation au carré, nous pouvons introduire des racines superflues. Assurez-vous de vérifier vos réponses !
Résoudre :\(x-3 \sqrt{x}+2=0\).
Solution :
Le\(\sqrt{x}\) à moyen terme, est au carré au premier terme\((\sqrt{x})^{2}=x\). Si nous le laissons\(u=\sqrt{x}\) et le remplaçons, notre trinôme sera en\(a x^{2}+b x+c=0\) forme.
| \(x-3 \sqrt{x}+2=0\) | |
| Réécrivez le trinôme pour préparer la substitution. | 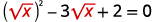 |
| Laisser\(u=\sqrt{x}\) et remplacer. | 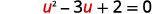 |
| Résolvez par factorisation. |
\((u-2)(u-1)=0\) \(u-2=0, \quad u-1=0\) |
| Remplacez\(u\) par\(\sqrt{x}\). |
\(\sqrt{x}=2, \quad \sqrt{x}=1\) |
| Résolvez pour\(x\), en quadrillant les deux côtés. | \(x=4, \quad x=1\) |
|
Vérifiez : 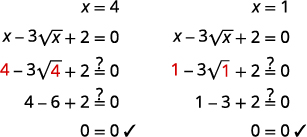 |
Résoudre :\(x-7 \sqrt{x}+12=0\).
- Réponse
-
\(x=9, x=16\)
Résoudre :\(x-6 \sqrt{x}+8=0\).
- Réponse
-
\(x=4, x=16\)
Les substitutions d'exposants rationnels peuvent également nous aider à résoudre une équation sous forme quadratique. Réfléchissez aux propriétés des exposants lorsque vous commencez l'exemple suivant.
Résoudre :\(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\).
Solution :
Le terme «\(x^{\frac{1}{3}}\) à moyen terme » est au carré au premier terme\(\left(x^{\frac{1}{3}}\right)^{2}=x^{\frac{2}{3}}\). Si nous le laissons\(u=x^{\frac{1}{3}}\) et le remplaçons, notre trinôme sera en\(a x^{2}+b x+c=0\) forme.
| \(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\) | |
| Réécrivez le trinôme pour préparer la substitution. | 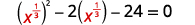 |
| Laissez\(u=x^{\frac{1}{3}}\) |  |
| Résolvez par factorisation. |
\((u-6)(u+4)=0\) \(u-6=0, \quad u+4=0\) \(u=6, \quad u=-4\) |
| Remplacez\(u\) par\(x^{\frac{1}{3}}\). |
\(x^{\frac{1}{3}}=6, \quad x^{\frac{1}{3}}=-4\) |
| Résolvez\(x\) le tout en coupant les deux côtés. |
\(\left(x^{\frac{1}{3}}\right)^{3}=(6)^{3}, \quad\left(x^{\frac{1}{3}}\right)^{3}=(-4)^{3}\) \(x=216, \quad x=-64\) |
|
Vérifiez : 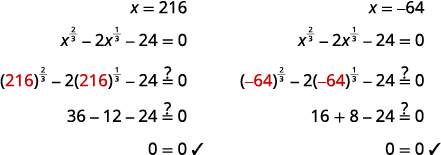
|
Résoudre :\(x^{\frac{2}{3}}-5 x^{\frac{1}{3}}-14=0\).
- Réponse
-
\(x=-8, x=343\)
Résoudre :\(x^{\frac{1}{2}}+8 x^{\frac{1}{4}}+15=0\).
- Réponse
-
\(x=81, x=625\)
Dans l'exemple suivant, nous devons garder à l'esprit la définition d'un exposant négatif ainsi que les propriétés des exposants.
Résoudre :\(3 x^{-2}-7 x^{-1}+2=0\).
Solution :
Le terme «\(x^{−1}\) à moyen terme » est au carré au premier terme\(\left(x^{-1}\right)^{2}=x^{-2}\). Si nous le laissons\(u=x^{−1}\) et le remplaçons, notre trinôme sera en\(a x^{2}+b x+c=0\) forme.
| \(3 x^{-2}-7 x^{-1}+2=0\) | |
| Réécrivez le trinôme pour préparer la substitution. | 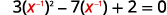 |
| Laisser\(u=x^{-1}\) et remplacer. | 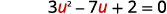 |
| Résolvez par factorisation. | \((3 u-1)(u-2)=0\) |
| \(3 u-1=0, \quad u-2=0\) | |
| \(u=\frac{1}{3}, \quad u=2\) | |
| Remplacez\(u\) par\(x^{-1}\). | \(x^{-1}=\frac{1}{3}, \quad x^{-1}=2\) |
| Résolvez\(x\) en prenant la réciproque depuis\(x^{-1}=\frac{1}{x}\). | \(x=3, \quad x=\frac{1}{2}\) |
|
Vérifiez : 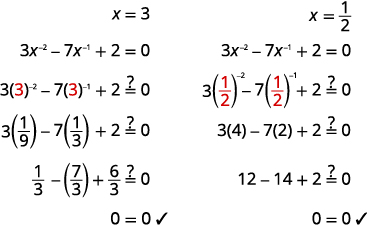
|
Résoudre :\(8 x^{-2}-10 x^{-1}+3=0\).
- Réponse
-
\(x=\frac{4}{3}, x=2\)
Résoudre :\(6 x^{-2}-23 x^{-1}+20=0\).
- Réponse
-
\(x=\frac{2}{5}, x=\frac{3}{4}\)
Accédez à cette vidéo en ligne pour obtenir des instructions et des exercices supplémentaires sur la résolution d'équations quadratiques : https://www.youtube.com/watch?v=7X-CZMbpxuw
Concepts clés
- Comment résoudre des équations sous forme quadratique.
- Identifiez une substitution qui mettra l'équation sous forme quadratique.
- Réécrivez l'équation avec la substitution pour la mettre sous forme quadratique.
- Résolvez l'équation quadratique pour\(u\).
- Remplacez la variable d'origine dans les résultats en utilisant la substitution.
- Résolvez pour la variable d'origine.
- Vérifiez les solutions.


