7.7 : Résoudre les inégalités rationnelles
- Page ID
- 194438
- Résolution des inégalités rationnelles
- Résoudre une inégalité grâce à des fonctions rationnelles
Avant de commencer, répondez à ce questionnaire de préparation.
- Trouvez la valeur de\(x-5\) quand ⓐ\(x=6\) ⓑ\(x=-3\) ⓒ\(x=5\)
Si vous avez oublié ce problème, consultez l'exemple 1.2.16. - Solution :\(8-2 x<12\)
Si vous avez oublié ce problème, consultez l'exemple 2.6.13. - Écrivez en notation par intervalles :\(-3 \leq x<5 \)
si vous avez oublié ce problème, consultez l'exemple 2.6.4.
Résolution des inégalités rationnelles
Nous avons appris à résoudre des inégalités linéaires après avoir appris à résoudre des équations linéaires. Les techniques étaient à peu près les mêmes, à une exception près. Lorsque nous multiplions ou divisons par un nombre négatif, le signe d'inégalité s'est inversé.
Comme nous venons d'apprendre à résoudre des équations rationnelles, nous sommes maintenant prêts à résoudre les inégalités rationnelles. Une inégalité rationnelle est une inégalité qui contient une expression rationnelle.
Une inégalité rationnelle est une inégalité qui contient une expression rationnelle.
Les inégalités telles que\(\quad \dfrac{3}{2 x}>1, \quad \dfrac{2 x}{x-3}<4, \quad \dfrac{2 x-3}{x-6} \geq x,\quad\) et\(\quad \dfrac{1}{4}-\dfrac{2}{x^{2}} \leq \dfrac{3}{x}\quad \) sont des inégalités rationnelles car elles contiennent chacune une expression rationnelle.
Lorsque nous résolvons une inégalité rationnelle, nous utiliserons de nombreuses techniques que nous avons utilisées pour résoudre les inégalités linéaires. Nous devons surtout nous rappeler que lorsque nous multiplions ou divisons par un nombre négatif, le signe d'inégalité doit s'inverser.
Une autre différence est que nous devons examiner attentivement quelle valeur pourrait rendre l'expression rationnelle non définie et doit donc être exclue.
Lorsque nous résolvons une équation et que le résultat est\(x=3\), nous savons qu'il existe une solution, qui est 3.
Lorsque nous résolvons une inégalité et que le résultat est\(x>3\), nous savons qu'il existe de nombreuses solutions. Nous illustrons le résultat pour mieux montrer toutes les solutions, et nous commençons par 3. Trois devient un point critique, puis nous décidons d'ombrer à gauche ou à droite de celui-ci. Les chiffres à droite de 3 sont supérieurs à 3, donc nous ombrons vers la droite.

Pour résoudre une inégalité rationnelle, il faut d'abord écrire l'inégalité avec un seul quotient à gauche et 0 à droite.
Ensuite, nous déterminons les points critiques à utiliser pour diviser la ligne numérique en intervalles. Un point critique est un nombre qui rend l'expression rationnelle nulle ou non définie.
Nous évaluerons ensuite les facteurs du numérateur et du dénominateur et trouverons le quotient dans chaque intervalle. Cela permettra d'identifier l'intervalle, ou les intervalles, qui contient toutes les solutions de l'inégalité rationnelle.
Nous écrivons la solution en notation par intervalles en prenant soin de déterminer si les points de terminaison sont inclus.
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{x-1}{x+3} \geq 0\)
Solution
Étape 1. Écrivez l'inégalité sous la forme d'un quotient à gauche et de zéro à droite.
Notre inégalité se présente sous cette forme. \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]
Étape 2. Déterminez les points critiques, c'est-à-dire les points où l'expression rationnelle sera nulle ou non définie.
L'expression rationnelle sera nulle lorsque le numérateur est égal à zéro. Depuis\(x-1=0\) quand\(x=1\), alors 1 est un point critique.
L'expression rationnelle ne sera pas définie lorsque le dénominateur est zéro. Depuis\(x+3=0\) quand\(x=-3\), -3 est un point critique.
Les points critiques sont 1 et -3.
Étape 3. Utilisez les points critiques pour diviser la ligne numérique en intervalles.
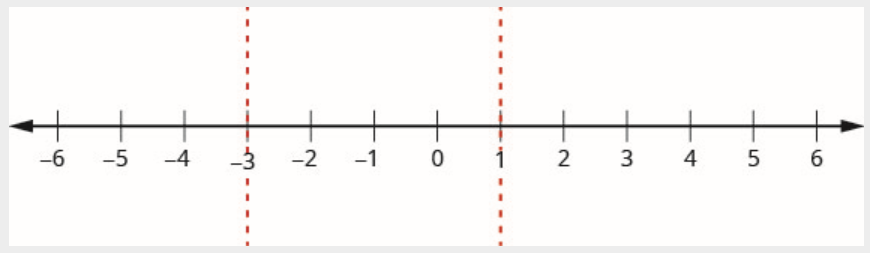
La ligne numérique est divisée en trois intervalles :
\[(-\infty,-3) \quad (-3,1) \quad (1,\infty) \nonumber \]
Étape 4. Testez une valeur dans chaque intervalle. Au-dessus de la ligne numérique, montrez le signe de chaque facteur de l'expression rationnelle dans chaque intervalle. Sous la ligne numérique, montrez le signe du quotient.
Pour trouver le signe de chaque facteur dans un intervalle, nous choisissons n'importe quel point de cet intervalle et l'utilisons comme point de test. N'importe quel point de l'intervalle donnera à l'expression le même signe, nous pouvons donc choisir n'importe quel point de l'intervalle.
\[\text { Interval }(-\infty,-3) \nonumber \]
Le chiffre -4 se trouve dans l'intervalle\((-\infty,-3)\). Testez\(x=-4\) l'expression au numérateur et au dénominateur.
Le numérateur :
\[\begin{array}{l} {x-1} \\ {-4-1} \\ {-5} \\ {\text {Negative}} \end{array} \nonumber \]
Le dénominateur :
\[\begin{array}{l} {x+3} \\ {-4+3} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]
Au-dessus de la ligne numérique, marquez le facteur\(x-1\) négatif et marquez le facteur\(x+3\) négatif.
Comme un négatif divisé par un négatif est positif, marquez le quotient positif dans l'intervalle\((-\infty,-3)\)
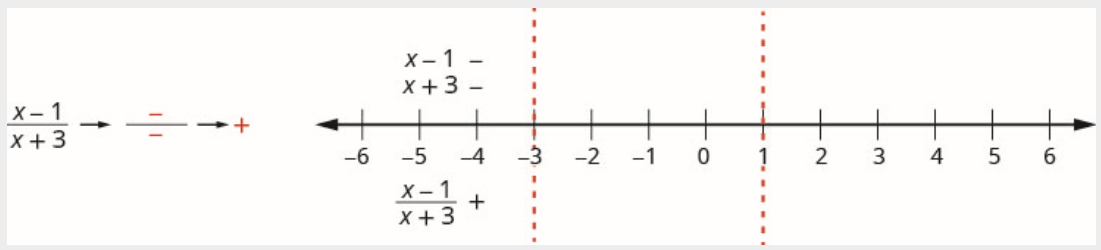
\[\text {Interval } (-3,1) \nonumber \]
Le chiffre 0 se trouve dans l'intervalle\((-3,1)\). Test\(x=0\).
Le numérateur :
\[\begin{array}{l} {x-1} \\ {0-1} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]
Le dénominateur :
\[\begin{array}{l} {x+3} \\ {0+3} \\ {3} \\ {\text {Positive}} \end{array} \nonumber \]
Au-dessus de la ligne numérique, marquez le facteur\(x-1\) négatif et marquez le\(x+3\) positif.
Comme un négatif divisé par un positif est négatif, le quotient est marqué comme négatif dans l'intervalle\((-3,1)\).
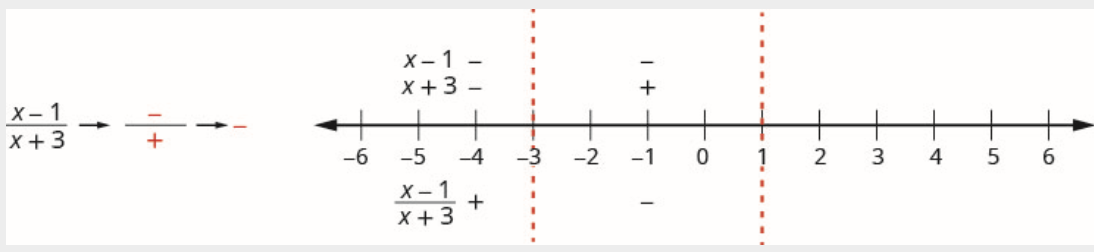
\[\text {Interval }(1, \infty) \nonumber \]
Le chiffre 2 se trouve dans l'intervalle\((1, \infty)\). Test\(x=2\).
Le numérateur :
\[\begin{array}{l} {x-1} \\ {2-1} \\ {1} \\ {\text {Positive}} \end{array} \nonumber \]
Le dénominateur :
\[\begin{array}{l} {x+3} \\ {2+3} \\ {5} \\ {\text {Positive}} \end{array} \nonumber \]
Au-dessus de la ligne numérique, marquez le facteur\(x-1\) positif et marquez-le\(x+3\) comme positif.
Comme un positif divisé par un positif est positif, marquez le quotient positif dans l'intervalle\((1, \infty)\).
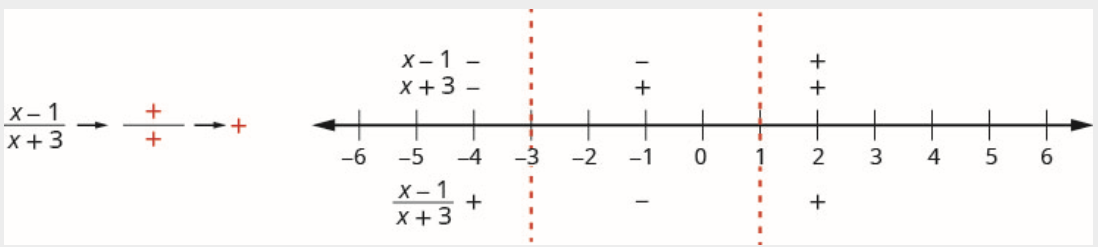
Étape 5. Déterminez les intervalles où l'inégalité est correcte. Écrivez la solution en notation par intervalles.
Nous voulons que le quotient soit supérieur ou égal à zéro, donc les nombres dans les intervalles\((-\infty,-3)\) et\((1, \infty) \) sont des solutions.
Mais qu'en est-il des points critiques ?
Le point critique\(x=-3\) fait du dénominateur 0, il doit donc être exclu de la solution et nous le marquons entre parenthèses.
Le point critique\(x=1\) fait de l'ensemble de l'expression rationnelle 0. L'inégalité exige que l'expression rationnelle soit supérieure ou égale à. Donc, 1 fait partie de la solution et nous allons le marquer avec un crochet.
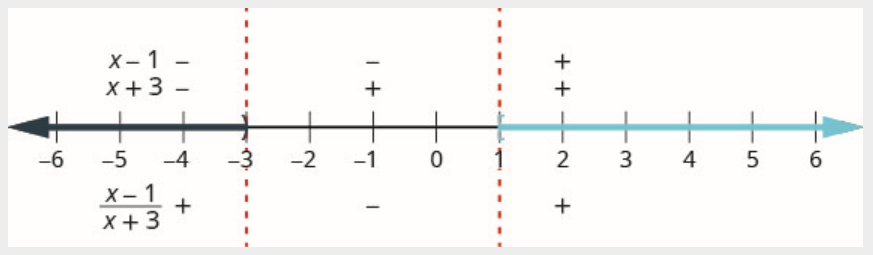
Rappelez-vous que lorsque nous avons une solution composée de plusieurs intervalles, nous utilisons le symbole d'union\(\cup \), pour relier les deux intervalles. La solution en notation par intervalles est\((-\infty,-3) \cup[1, \infty)\).
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{x-2}{x+4} \geq 0\)
- Réponse
-
\((-\infty,-4) \cup[2, \infty)\)
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{x+2}{x-4} \geq 0\)
- Réponse
-
\((-\infty,-2] \cup(4, \infty)\)
Nous résumons les étapes pour faciliter la consultation.
Étape 1 Écrivez l'inégalité sous la forme d'un quotient à gauche et de zéro à droite.
Étape 2 Déterminez les points critiques, c'est-à-dire les points où l'expression rationnelle sera nulle ou non définie.
Étape 3. Utilisez les points critiques pour diviser la ligne numérique en intervalles.
Étape 4. Testez une valeur dans chaque intervalle. Au-dessus de la ligne numérique, montrez le signe de chaque facteur du numérateur et du dénominateur dans chaque intervalle. Sous la ligne numérique, montrez le signe du quotient.
Étape 5. Déterminez les intervalles où l'inégalité est correcte. Écrivez la solution en notation par intervalles.
L'exemple suivant exige que nous mettions d'abord l'inégalité rationnelle sous la forme correcte.
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{4 x}{x-6}<1\)
Solution
\[\dfrac{4 x}{x-6}<1 \nonumber \]
Soustrayez 1 pour obtenir zéro sur la droite.
\[\dfrac{4 x}{x-6}-1<0 \nonumber \]
Réécrivez 1 sous forme de fraction à l'aide de l'écran LCD.
\[\dfrac{4 x}{x-6}-\frac{x-6}{x-6}<0 \nonumber \]
Soustrayez les numérateurs et placez la différence au-dessus du dénominateur commun.
\[\dfrac{4 x-(x-6)}{x-6}<0 \nonumber \]
Simplifiez.
\[\dfrac{3 x+6}{x-6}<0 \nonumber \]
Facturez le numérateur pour afficher tous les facteurs.
\[\dfrac{3(x+2)}{x-6}<0 \nonumber \]
Trouvez les points critiques.
Le quotient sera nul lorsque le numérateur est nul. Le quotient n'est pas défini lorsque le dénominateur est nul.
\[\begin{array}{rlrl} {x+2} & {=0} & {x-6} & {=0} \\ {x} & {=-2} & {x} & {=6} \end{array} \nonumber \]
Utilisez les points critiques pour diviser la ligne numérique en intervalles.
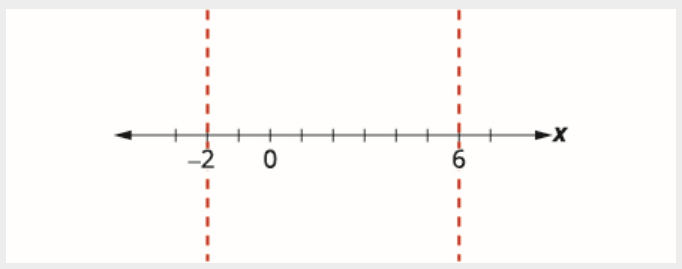
Testez une valeur dans chaque intervalle.
| \((-\infty,-2)\) | \((-2,6)\) | \((6, \infty)\) | |
|---|---|---|---|
| \(x+2)\) | \ (- \ infty, -2) \) » style="vertical-align:middle ; » class="lt-math-5164">
x+2 -3+2 -1 - |
\ (-2,6) \) » style="vertical-align:middle ; » class="lt-math-5164">
x+2 0+2 2 + |
\ (6, \ infty) \) » style="vertical-align:middle ; » class="lt-math-5164">
x+2 7+2 9 + |
| \(x-6\) | \ (- \ infty, -2) \) » style="vertical-align:middle ; » class="lt-math-5164">
x-6 3-6 -9 - |
\ (-2,6) \) » style="vertical-align:middle ; » class="lt-math-5164">
x-6 0-6 -6 - |
\ (6, \ infty) \) » style="vertical-align:middle ; » class="lt-math-5164">
x-6 7-6 1 + |
Au-dessus de la ligne numérique, montrez le signe de chaque facteur de l'expression rationnelle dans chaque intervalle. Sous la ligne numérique, montrez le signe du quotient.
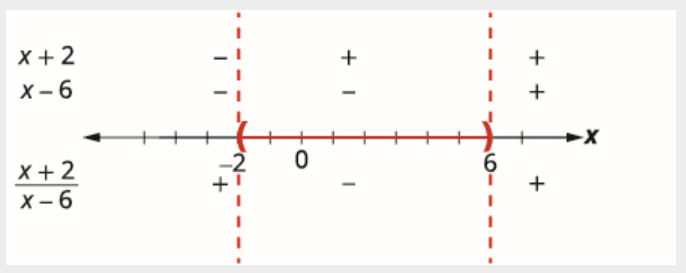
Déterminez les intervalles où l'inégalité est correcte. Nous voulons que le quotient soit négatif, de sorte que la solution inclut les points compris entre −2 et 6. Comme l'inégalité est strictement inférieure à, les paramètres ne sont pas inclus.
Nous écrivons la solution en notation par intervalles sous la forme (−2, 6).
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{3 x}{x-3}<1\).
- Réponse
-
\(\left(-\dfrac{3}{2}, 3\right)\)
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{3 x}{x-4}<2\).
- Réponse
-
\((-8,4)\)
Dans l'exemple suivant, le numérateur est toujours positif, de sorte que le signe de l'expression rationnelle dépend du signe du dénominateur.
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{5}{x^{2}-2 x-15}>0\).
Solution
L'inégalité prend la bonne forme.
\[\dfrac{5}{x^{2}-2 x-15}>0 \nonumber \]
Facturez le dénominateur.
\[\dfrac{5}{(x+3)(x-5)}>0 \nonumber \]
Trouvez les points critiques. Le quotient est égal à 0 lorsque le numérateur est égal à 0. Comme le numérateur est toujours 5, le quotient ne peut pas être égal à 0.
Le quotient ne sera pas défini lorsque le dénominateur est nul.
\[\begin{aligned} &(x+3)(x-5)=0\\ &x=-3, x=5 \end{aligned} \nonumber \]
Utilisez les points critiques pour diviser la ligne numérique en intervalles.
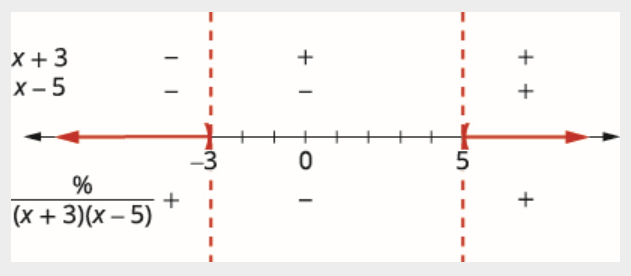
Testez les valeurs dans chaque intervalle. Au-dessus de la ligne numérique, indiquez le signe de chaque facteur du dénominateur dans chaque intervalle. Sous la ligne numérique, montrez le signe du quotient.
Écrivez la solution en notation par intervalles.
\[(-\infty,-3) \cup(5, \infty) \nonumber \]
Solve and write the solution in interval notation: \(\dfrac{1}{x^{2}+2 x-8}>0\).
- Answer
-
\((-\infty,-4) \cup(2, \infty)\)
Solve and write the solution in interval notation: \(\dfrac{3}{x^{2}+x-12}>0 \).
- Answer
-
\((-\infty,-4) \cup(3, \infty)\)
The next example requires some work to get it into the needed form.
Solve and write the solution in interval notation: \(\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x}\).
Solution
\[\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x} \nonumber \]
Subtract \(\dfrac{5}{3 x}\) to get zero on the right.
\[\dfrac{1}{3}-\dfrac{2}{x^{2}}-\dfrac{5}{3 x}<0 \nonumber \]
Rewrite to get each fraction with the LCD
\[\dfrac{1 \cdot x^{2}}{3 \cdot x^{2}}-\dfrac{2 \cdot 3}{x^{2} \cdot 3}-\dfrac{5 \cdot x}{3 x-x}<0 \nonumber \]
Simplify.
\[\dfrac{x^{2}}{3 x^{2}}-\dfrac{6}{3 x^{2}}-\dfrac{5 x}{3 x^{2}}<0 \nonumber \]
Subtract the numerators and place the difference over the common denominator.
\[\dfrac{x^{2}-5 x-6}{3 x^{2}}<0 \nonumber \]
Factor the numerator.
\[\dfrac{(x-6)(x+1)}{3 x^{2}}<0 \nonumber \]
Find the critical points.
\[\begin{array}{rlrl} {3 x^{2}=0} && {x-6=0} && {x+1=0} \\ {x=0} && {x=6} && {x=-1} \end{array} \nonumber \]
Use the critical points to divide the number line into intervals.
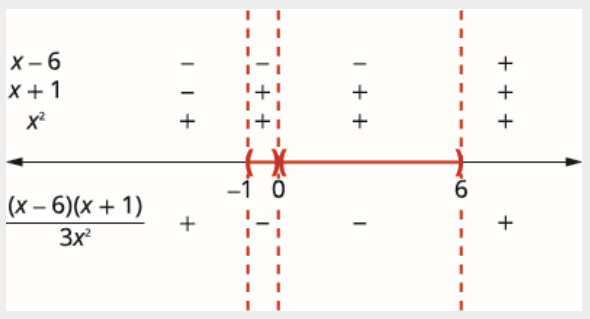
Au-dessus de la ligne numérique, montrez le signe de chaque facteur dans chaque intervalle. Sous la ligne numérique, montrez le signe du quotient.
Puisque 0 est exclu, la solution est constituée des deux\((-1,0) \cup(0,6)\) intervalles\((-1,0)\) et\((0,6)\).
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{1}{2}+\dfrac{4}{x^{2}}<\dfrac{3}{x}\).
- Réponse
-
\((2,4)\)
Résolvez et écrivez la solution en notation par intervalles :\(\dfrac{1}{3}+\dfrac{6}{x^{2}}<\dfrac{3}{x}\).
- Réponse
-
\((3,6)\)
Résolvez une inégalité avec des fonctions rationnelles
Lorsque vous travaillez avec des fonctions rationnelles, il est parfois utile de savoir si la fonction est supérieure ou inférieure à une valeur donnée. Cela conduit à une inégalité rationnelle.
\(R(x)=\dfrac{x+3}{x-5}\)En fonction de la fonction, trouvez les valeurs de x qui rendent la fonction inférieure ou égale à 0.
Solution
Nous voulons que la fonction soit inférieure ou égale à 0.
\[R(x) \leq 0 \nonumber \]
Remplacez l'expression rationnelle par\(R(x)\).
\[\dfrac{x+3}{x-5} \leq 0 \quad x \neq 5 \nonumber \]
Trouvez les points critiques.
\[\begin{array}{rlrl} {x+3=0} && {x-5=0} \\ {x=-3} && {x=5} \end{array} \nonumber \]
Utilisez les points critiques pour diviser la ligne numérique en intervalles.
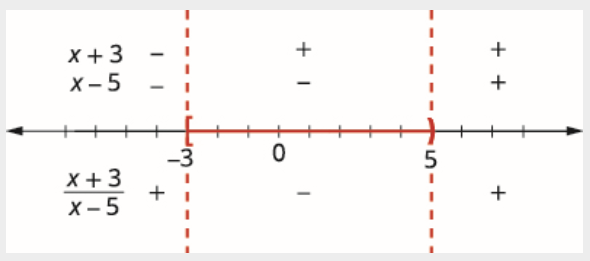
Testez les valeurs dans chaque intervalle. Au-dessus de la ligne numérique, montrez le signe de chaque facteur dans chaque intervalle. Sous la ligne numérique, montrez le signe du quotient. Écrivez la solution en notation par intervalles. Puisque 5 est exclu, nous ne l'incluons pas dans l'intervalle.
\[[-3,5) \nonumber \]
Given the function \(R(x)=\dfrac{x-2}{x+4}\), find the values of \(x\) that make the function less than or equal to 0.
- Answer
-
\((-4,2]\)
Given the function \(R(x)=\dfrac{x+1}{x-4}\), find the values of \(x\) that make the function less than or equal to 0.
- Answer
-
\([-1,4)\)
In economics, the function \(C(x)\) is used to represent the cost of producing \(x\) units of a commodity. The average cost per unit can be found by dividing \(C(x)\) by the number of items \(x\). Then, the average cost per unit is \(c(x)=\dfrac{C(x)}{x}).
The function\(C(x)=10 x+3000\) represents the cost to produce \(x\), number of items. Find:
- The average cost function, \(c(x)\)
- How many items should be produced so that the average cost is less than $40.
Solution
- \[C(x)=10 x+3000 \nonumber \]
The average cost function is \(c(x)=\dfrac{C(x)}{x})\). To find the average cost function, divide the cost function by \(x\).
\[\begin{aligned} &c(x)=\dfrac{C(x)}{x}\\ &c(x)=\dfrac{10 x+3000}{x} \end{aligned} \nonumber \]
The average cost function is \(c(x)=\dfrac{10 x+3000}{x} \)
- We want the function \(c(x)\) to be less than 40.
\[c(x)<40 \nonumber \]
Substitute the rational expression forc(x).
\[\dfrac{10 x+3000}{x}<40, \quad x \neq 0 \nonumber \]
Subtract 40 to get 0 on the right.
\[\dfrac{10 x+3000}{x}-40<0 \nonumber \]
Rewrite the left side as one quotient by finding the LCD and performing the subtraction.
\[\begin{aligned} \dfrac{10 x+3000}{x}-40\left(\dfrac{x}{x}\right) &<0\\ \dfrac{10 x+3000}{x}-\dfrac{40 x}{x} &<0\\ \dfrac{10 x+3000-40 x}{x} &<0 \\ \dfrac{-30 x+3000}{x} &<0 \end{aligned} \nonumber \]
Factor the numerator to show all factors.
\[\begin{array}{ll} {\dfrac{-30(x-100)}{x}<0} \\ {-30(x-100)=0} && {x=0} \end{array} \nonumber \]
Find the critical points.
\[\begin{array}{rl} {-30 \neq 0} & {x-100=0} \\ &{x=100} \end{array} \nonumber \]
More than 100 items must be produced to keep the average cost below $40 per item.
The function\(C(x)=20 x+6000\) represents the cost to produce \(x\), number of items. Find:
- How many items should be produced so that the average cost is less than $60.
- Answer
-
- \(c(x)=\dfrac{20 x+6000}{x}\)
- More than 150 items must be produced to keep the average cost below $60 per item.
The function\(C(x)=5 x+900\) represents the cost to produce \(x\), number of items. Find:
- How many items should be produced so that the average cost is less than $20.
- Answer
-
- \(c(x)=\dfrac{5 x+900}{x}\)
- More than 60 items must be produced to keep the average cost below $20 per item.


