Skip to main content
Global

7.6 : Résolvez des applications avec des équations

  1. Last updated
  2. Save as PDF
  • Page ID
    194403

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • Résoudre les proportions
    • Résolvez des applications avec des
    • Résolvez des applications de mouvement
    • Résoudre les applications professionnelles
    • Résoudre les problèmes de variation directe
    • Résoudre les problèmes de variation inverse
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Exemple 2.2.13. Exemple 2.5.13. Exemple 2.2.9.

    Résoudre les proportions

    Lorsque deux expressions rationnelles sont égales, l'équation qui les relie est appelée proportion.

    Proportion

    Une proportion est une équation de la forme\(\dfrac{a}{b}=\dfrac{c}{d}\), où\(b \neq 0, d \neq 0\).

    La proportion se lit comme suit : «\(a\)\(b\) tel\(c\) quel »\(d\).

    L'équation\(\dfrac{1}{2}=\dfrac{4}{8}\) est une proportion car les deux fractions sont égales. La proportion\(\dfrac{1}{2}=\dfrac{4}{8}\) se lit comme suit : « 1 vaut pour 2 et 4 pour 8 ».

    Comme une proportion est une équation avec des expressions rationnelles, nous allons résoudre les proportions de la même manière que nous avons résolu des équations rationnelles. Nous allons multiplier les deux côtés de l'équation par l'écran LCD pour effacer les fractions, puis résoudre l'équation résultante.

    Exemple\(\PageIndex{1}\)

    Résoudre :\(\dfrac{n}{n+14}=\dfrac{5}{7}\).

    Solution

    \[\dfrac{n}{n+14}=\dfrac{5}{7}, \quad n \neq-14 \nonumber \]

    Multipliez les deux côtés par LCD.

    \[7(n+14)\left(\dfrac{n}{n+14}\right)=7(n+14)\left(\dfrac{5}{7}\right) \nonumber \]

    Supprimez les facteurs communs de chaque côté.

    \[7 n=5(n+14) \nonumber \]

    Simplifiez.

    \[7 n=5 n+70 \nonumber \]

    Résolvez pour\(n\).

    \[\begin{aligned} 2n&=70\\ n&=35 \end{aligned} \nonumber \]

    Vérifiez.

    \[\dfrac{n}{n+14}=\dfrac{5}{7} \nonumber \]

    substitut\(n=35\)

    \[\dfrac{35}{35+14} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    Simplifiez.

    \[\dfrac{35}{49} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    Afficher les facteurs communs.

    \[\dfrac{5 \cdot 7}{7 \cdot 7} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    Simplifiez.

    \[\dfrac{5}{7}=\dfrac{5}{7}\; \surd \nonumber \]

    Exercice\(\PageIndex{1}\)

    Résolvez la proportion :\(\dfrac{y}{y+55}=\dfrac{3}{8}\).

    Réponse

    \(y=33\)

    Exercice\(\PageIndex{2}\)

    Résolvez la proportion :\(\dfrac{z}{z-84}=-\dfrac{1}{5}\).

    Réponse

    \(z=14\)

    Remarquez dans le dernier exemple que lorsque nous avons effacé les fractions en les multipliant par l'écran LCD, le résultat est le même que si nous avions fait une multiplication croisée.

    \[\begin{aligned} \dfrac{n}{n+14}=\dfrac{5}{7} \quad \quad \quad \dfrac{n}{n+14}=\dfrac{5}{7} \\ 7(n+14)\left(\dfrac{n}{n+14}\right)=7(n+14)\left(\dfrac{5}{7}\right) \quad \quad \quad \dfrac{n}{n+14}=\dfrac{5}{7} \\ 7n=5(n+14) \quad \quad \quad 7n=5(n+14) \end{aligned} \nonumber \]

    Quelle que soit la proportion\(\dfrac{a}{b}=\dfrac{c}{d}\), nous obtenons le même résultat lorsque nous effaçons les fractions en les multipliant par l'écran LCD que lorsque nous effectuons une multiplication croisée.

    \[\begin{aligned} \dfrac{a}{b} =\dfrac{c}{d} \quad \quad \quad \dfrac{a}{b}=\dfrac{c}{d} \\ bd\left(\dfrac{a}{b}=\frac{c}{d}\right) bd \quad \quad \quad \frac{a}{b} = \frac{c}{d} \\ ad =bc \quad \quad \quad ad=bc \end{aligned} \nonumber \]

    Pour résoudre des applications avec des proportions, nous suivrons notre stratégie habituelle de résolution des applications. Mais lorsque nous définissons la proportion, nous devons nous assurer que les unités des numérateurs doivent correspondre les unes aux autres et les unités des dénominateurs doivent également correspondre les unes aux autres.

    Lorsque les pédiatres prescrivent de l'acétaminophène à des enfants, ils prescrivent 5 millilitres (ml) d'acétaminophène pour chaque tranche de 25 livres de poids de l'enfant. Si Zoé pèse 80 livres, combien de millilitres d'acétaminophène son médecin prescrira-t-il ?

    Solution

    Identifiez ce que l'on nous demande de trouver et choisissez une variable pour le représenter.

    Combien de ml d'acétaminophène le médecin vous prescrira-t-il ?

    Laisse\(a=ml\) de l'acétaminophène.

    Écrivez une phrase qui donne les informations nécessaires pour le trouver.

    Si 5 ml sont prescrits pour 25 livres, quelle quantité sera prescrite pour 80 livres ?

    Traduisez en proportion, faites attention aux unités.

    Étape 1 Écrivez l'inégalité sous la forme d'un quotient à gauche et de zéro à droite. Notre inégalité se présente sous cette forme.

    \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]

    Étape 2 Déterminez les points critiques, c'est-à-dire les points où l'expression rationnelle sera nulle ou non définie.

    L'expression rationnelle sera nulle lorsque le numérateur est nul. Depuis\(x-1=0\) quand\(x=1\), alors 1 est un point critique. L'expression rationnelle ne sera pas définie lorsque le dénominateur est zéro. Depuis\(x+3=0\) quand\(x=-3\), -3 est un point critique.

    Étape 3. Utilisez les points critiques pour diviser la ligne numérique en intervalles.

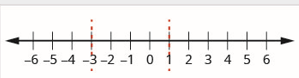
    clipboard_ee2fe708799269f0539168f8443a351d2.png

    Étape 4. Au-dessus de la ligne numérique, montrez le signe de chaque facteur de l'expression rationnelle dans chaque intervalle. Sous la ligne numérique, montrez le signe du quotient.

    Utilisez les valeurs de chaque intervalle pour déterminer la valeur de chaque facteur de l'intervalle. Dans l'intervalle (-3,1), zéro est une bonne valeur à tester. Par exemple, lorsque\(x=0\) alors\(x-1=-1\) et\(x+3=3\) Le facteur\(x-1\) est marqué comme négatif et\(x+3\) marqué comme positif. Comme un négatif divisé par un positif est négatif, le quotient est marqué comme négatif dans cet intervalle.

    Étape 5. Déterminez les intervalles où l'inégalité est correcte. Écrivez la solution en notation par intervalles.

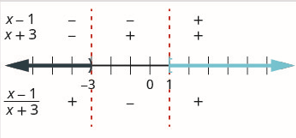
    clipboard_edae13eef9fc14a8139b8d2bcd44dd965.png

    Nous voulons que le quotient soit supérieur ou égal à zéro, donc les nombres dans les intervalles\((-\infty,-3)\) et\((1, \infty)\) sont des solutions. Puisque 3 doit être exclu puisqu'il fait de l'expression rationnelle 0, nous ne pouvons pas l'inclure dans la solution. Nous pouvons en inclure 1 dans notre solution.

    \[(-\infty,-3) \cup[1, \infty) \nonumber \]

    Multipliez les deux côtés par l'écran LCD, 400. Supprimez les facteurs communs de chaque côté. Simplifiez, mais ne multipliez pas sur la gauche. Remarquez quelle sera la prochaine étape.

    \[16 \cdot 5=5 a \nonumber \]

    Résolvez pour\(a\).

    \[\begin{aligned} \dfrac{16 \cdot 5}{5}&=\dfrac{5 a}{5}\\ 16&=a \end{aligned} \nonumber \]

    Vérifiez. La réponse est-elle raisonnable ? Écrivez une phrase complète.

    Le pédiatre prescrirait 16 ml d'acétaminophène à Zoé.

    Exercice\(\PageIndex{3}\)

    Les pédiatres prescrivent 5 millilitres (ml) d'acétaminophène pour chaque tranche de 25 livres de poids d'un enfant. Combien de millilitres d'acétaminophène le médecin prescrira-t-il à Emilia, qui pèse 60 livres ?

    Réponse

    Le pédiatre prescrira 12 ml d'acétaminophène à Emilia.

    Exercice\(\PageIndex{4}\)

    Pour chaque kilogramme (kg) de poids d'un enfant, les pédiatres prescrivent 15 milligrammes (mg) d'un antifièvre. Si Isabella pèse 12 kg, combien de milligrammes de réducteur de fièvre le pédiatre prescrira-t-il ?

    Réponse

    Le pédiatre prescrira 180 mg de réducteur de fièvre à Isabella.

    Résolvez des applications avec des

    Lorsque vous réduisez ou agrandissez une photo sur un téléphone ou une tablette, que vous déterminez une distance sur une carte, que vous utilisez un motif pour construire une bibliothèque ou coudre une robe, vous travaillez avec des figures similaires. Si deux figures ont exactement la même forme, mais des tailles différentes, on dit qu'elles sont similaires. L'un est une maquette de l'autre. Tous leurs angles correspondants ont les mêmes mesures et leurs côtés correspondants ont le même rapport.

    Figurines similaires

    Deux figures sont similaires si les mesures de leurs angles correspondants sont égales et que leurs côtés correspondants ont le même rapport.

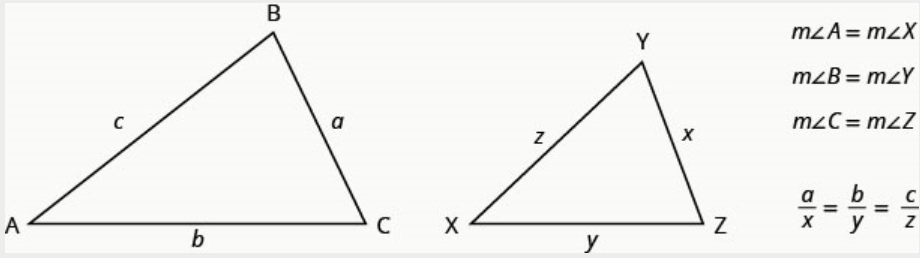
    Par exemple, les deux triangles de la figure ci-dessous sont similaires. Chaque côté de \(\Delta ABC\)est quatre fois plus long que le côté correspondant de \(\Delta XYZ\).

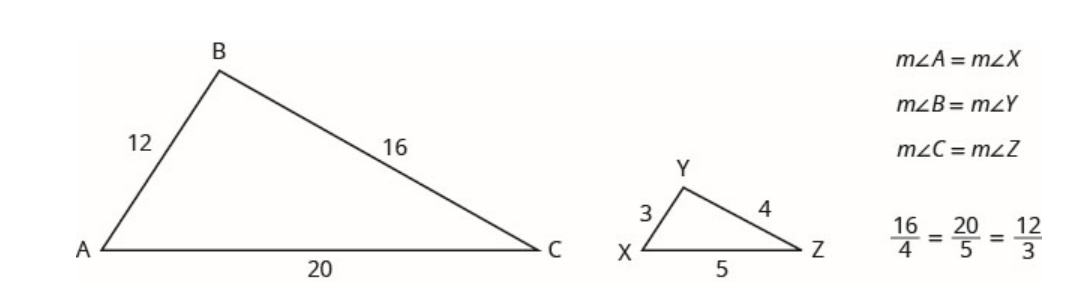
    clipboard_e856a7de8b3a79dcd08723d9871ccd270.png

    Ceci est résumé dans la propriété des triangles similaires.

    Propriété de triangles similaires

    Si\(\Delta ABC\) est similaire à\(\Delta XYZ\), alors leur mesure d'angle correspondante est égale et leurs côtés correspondants ont le même rapport.

    clipboard_e4fdc3b30588979c50d44a48aef0d74a0.png

    Pour résoudre des applications avec des chiffres similaires, nous suivrons la stratégie de résolution de problèmes pour les applications de géométrie que nous avons utilisée précédemment.

    Exemple\(\PageIndex{3}\)

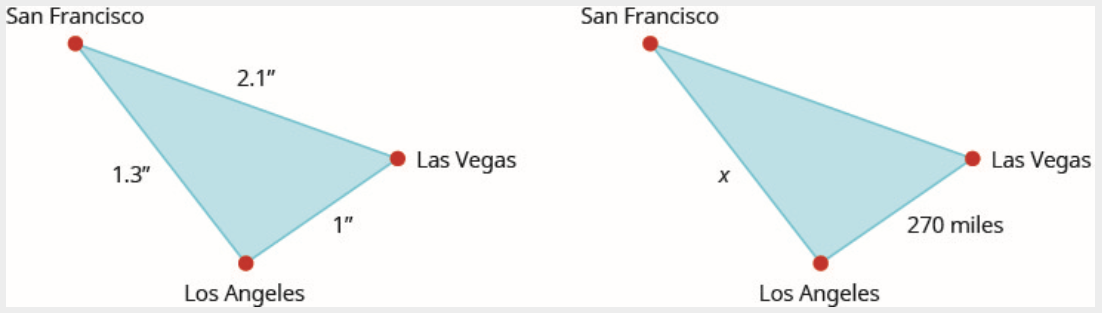
    Sur une carte, San Francisco, Las Vegas et Los Angeles forment un triangle. La distance entre les villes est mesurée en pouces. La figure de gauche ci-dessous représente le triangle formé par les villes sur la carte. Si la distance réelle entre Los Angeles et Las Vegas est de 270 miles, trouvez la distance entre Los Angeles et San Francisco.

    clipboard_efb0263e1d94381d6b9257775d879ded0.png

    Solution

    Les triangles étant similaires, les côtés correspondants sont proportionnels.

    Lisez le problème. Dessinez les figures et étiquetez-les avec les informations données. Les chiffres sont présentés ci-dessus.

    Identifiez ce que nous recherchons : la distance réelle entre Los Angeles et San Francisco

    Nommez les variables : Let\(x\) = distance entre Los Angeles et San Francisco.

    Traduisez en une équation. Les triangles étant similaires, les côtés correspondants sont proportionnels. Nous allons faire les numérateurs « miles » et les dénominateurs « pouces ».

    \[$\dfrac{x \text { miles }}{1.3 \text { inches }}=\dfrac{270 \text { miles }}{1 \text { inch }}$ \nonumber \]

    Résolvez l'équation.

    \[\begin{aligned} 1.3\left(\dfrac{x}{1.3}\right)&=1.3\left(\dfrac{270}{1}\right) \\ x&=351 \end{aligned} \nonumber \]

    Vérifiez. Sur la carte, la distance entre Los Angeles et San Francisco est supérieure à la distance entre Los Angeles et Las Vegas. Puisque 351 est plus que 270, la réponse est logique.

    Vérifiez\(x=351\) les proportions d'origine. Utilisez une calculatrice.

    \[\begin {aligned} \dfrac{x \text { miles }}{1.3 \text { inches }}&=\dfrac{270 \text { miles }}{1 \text { inch }}\\ \dfrac{351 \text { miles }}{1.3 \text { inches }} &\overset{?}{=} \dfrac{270 \text { miles }}{1 \text { inch }}\\ \dfrac{270 \text { miles }}{1 \text { inch }}&=\dfrac{270 \text { miles }}{1 \text { inch }} \surd \end{aligned} \nonumber \]

    Répondez à la question : La distance entre Los Angeles et San Francisco est de 351 miles.

    Sur la carte, Seattle, Portland et Boise forment un triangle. La distance entre les villes est mesurée en pouces. La figure de gauche ci-dessous représente le triangle formé par les villes sur la carte. La distance réelle entre Seattle et Boise est de 400 miles.

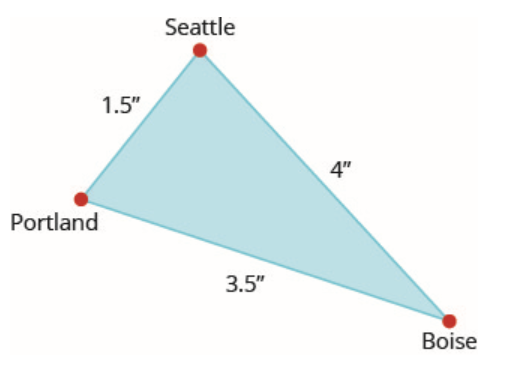
    clipboard_e545a49106f741f6a3b36f53e39ed4458.png

    Exercice\(\PageIndex{5}\)

    Trouver la distance réelle entre Seattle et Portland.

    Réponse

    La distance est de 150 miles.

    Exercice\(\PageIndex{6}\)

    Trouver la distance réelle entre Portland et Boise.

    Réponse

    La distance est de 350 miles.

    Nous pouvons utiliser des chiffres similaires pour trouver des hauteurs que nous ne pouvons pas mesurer directement.

    Exemple\(\PageIndex{4}\)

    Tyler mesure 6 pieds. En fin d'après-midi, son ombre mesurait 8 pieds de long. Au même moment, l'ombre d'un arbre mesurait 24 pieds de long. Trouve la hauteur de l'arbre.

    Solution

    Lisez le problème et dessinez une figure. Nous cherchons\(h\) la hauteur de l'arbre.

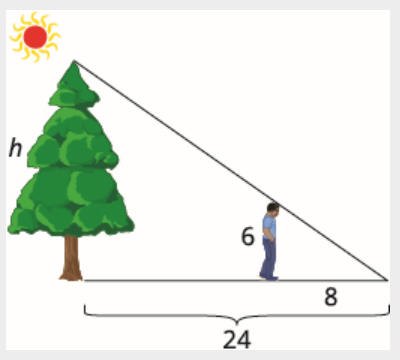
    clipboard_ee900ec650dd61d33cbc8b7d340874f27.png

    Nous utiliserons des triangles similaires pour écrire une équation. Le petit triangle est similaire au grand triangle.

    \[\dfrac{h}{24}=\dfrac{6}{8} \nonumber \]

    Résolvez la proportion.

    \[\begin {aligned} 24\left(\dfrac{6}{8}\right)&=24\left(\dfrac{h}{24}\right)\\ 18&=h \end{aligned} \nonumber \]

    Simplifiez. Vérifiez.

    La hauteur de Tyler est inférieure à la longueur de son ombre, il est donc logique que la hauteur de l'arbre soit inférieure à la longueur de son ombre. Vérifiez\(h=18\) les proportions d'origine.

    \[\begin{aligned} &\dfrac{6}{8}=\dfrac{h}{24}\\ &\dfrac{6}{8} \overset{?}{=} \dfrac{18}{24}\\ &\dfrac{3}{4}=\dfrac{3}{4} \surd \end{aligned} \nonumber \]

    Exercice\(\PageIndex{7}\)

    Un poteau téléphonique projette une ombre de 50 pieds de long. À proximité, un panneau de signalisation de 8 pieds de haut projette une ombre de 10 pieds de long. Quelle est la hauteur du poteau téléphonique ?

    Réponse

    Le poteau téléphonique mesure 40 pieds de haut.

    Exercice\(\PageIndex{8}\)

    Un pin projette une ombre de 80 pieds à côté d'un bâtiment de 30 pieds de haut qui projette une ombre de 40 pieds. Quelle est la hauteur du pin ?

    Réponse

    Le pin mesure 60 pieds de haut.

    Résolvez des applications de mouvements

    Nous avons résolu les problèmes de mouvement uniforme en utilisant la formule\(D=r t\) des chapitres précédents. Nous avons utilisé un tableau comme celui ci-dessous pour organiser les informations et nous amener à l'équation.

    Tarif :\(\cdot\) temps = distance
      \ (\ cdot \) Temps = Distance » class="lt-math-14671">    
      \ (\ cdot \) Temps = Distance » class="lt-math-14671">    

    La formule\(D=r t\) suppose que nous les connaissons\(r\)\(t\) et que nous les utilisons pour les trouver\(D\). Si nous savons\(D\)\(r\) et avons besoin de trouver\(t\), nous résoudrons l'équation pour\(t\) obtenir la formule\(t=\dfrac{D}{r}\).

    Nous avons également expliqué comment le fait de voler avec ou contre le vent affecte la vitesse d'un avion. Nous reviendrons sur cette idée dans l'exemple suivant.

    Exemple\(\PageIndex{5}\)

    Un avion peut parcourir 200 miles dans un vent de face de 30 mi/h dans le même laps de temps qu'il faut pour parcourir 300 miles avec un vent arrière de 30 mi/h. Quelle est la vitesse de l'avion ?

    Solution

    Il s'agit d'une situation de mouvement uniforme. Un diagramme nous aidera à visualiser la situation.

    clipboard_e675478d490b6955418a9d40f7346c6b5.png

    Nous remplissons le tableau pour organiser les informations.

    Nous cherchons la vitesse de l'avion. Soit\(r\) la vitesse de l'avion.

    Lorsque l'avion vole avec le vent, le vent augmente sa vitesse et donc la vitesse\(r + 30\).

    Lorsque l'avion vole contre le vent, le vent diminue sa vitesse et la vitesse diminue\(r − 30\).

    Inscrivez les tarifs. Inscrivez les distances. Depuis\(D=r \cdot t\), nous résolvons\(t\) et obtenons\(t=\dfrac{D}{r}\). Nous divisons la distance par le taux de chaque ligne et plaçons l'expression dans la colonne temporelle.

    Tarif :\(\cdot\) temps = distance
    Vent de face \ (\ cdot \) Temps = distance">\(r-30\) \(\dfrac{200}{r-30}\) 200
    Vent arrière \ (\ cdot \) Temps = distance">\(r+30\) \(\dfrac{300}{r+30}\) 300

    Nous savons que les temps sont égaux et nous écrivons donc notre équation.

    \[\dfrac{200}{r-30}=\dfrac{300}{r+30} \nonumber \]

    Nous multiplions les deux côtés par l'écran LCD.

    \[(r+30)(r-30)\left(\frac{200}{r-30}\right)=(r+30)(r-30)\left(\frac{300}{r+30}\right) \nonumber \]

    Simplifiez et résolvez.

    \[\begin{aligned} (r+30)(200)&=(r-30) 300 \\ 200 r+6000&=300 r-9000 \\ 15000&=100 r \end{aligned} \nonumber \]

    Vérifiez.

    La vitesse\(150 \mathrm{mph}\) d'un avion est-elle raisonnable ? Oui. Si l'avion voyage\(150 \mathrm{mph}\) et que le vent le fait\(30 \mathrm{mph}\),

    \[\text { Tailwind } \quad 150+30=180 \mathrm{mph} \quad \dfrac{300}{180}=\dfrac{5}{3} \text { hours } \nonumber \]

    \[\text { Headwind } 150-30=120 \mathrm{mph} \dfrac{200}{120}=\dfrac{5}{3} \text { hours } \nonumber \]

    Les temps sont égaux, donc ça vérifie. L'avion voyageait\(150 \mathrm{mph}\).

    Exercice\(\PageIndex{9}\)

    Link peut faire du vélo sur 20 miles dans un vent de face de 3 mi/h en même temps qu'il peut parcourir 30 miles avec un vent arrière de 3 mi/h. Quelle est la vitesse à vélo de Link ?

    Réponse

    La vitesse de vélo de Link est de 15 km/h.

    Exercice\(\PageIndex{10}\)

    Danica peut naviguer sur son bateau à 5 miles dans un vent de face de 7 mi/h en même temps qu'elle peut parcourir 12 miles avec un vent arrière de 7 mi/h. Quelle est la vitesse du bateau de Danica sans vent ?

    Réponse

    La vitesse du bateau de Danica est de 17 mi/h.

    Dans l'exemple suivant, nous connaîtrons le temps total résultant du fait de parcourir différentes distances à différentes vitesses.

    Exemple\(\PageIndex{6}\)

    Jazmine s'est entraînée pendant 3 heures samedi. Elle a couru 8 miles puis a fait 24 miles à vélo. Sa vitesse de vélo est 4 mi/h plus rapide que sa vitesse de course. Quelle est sa vitesse de course ?

    Solution

    Il s'agit d'une situation de mouvement uniforme. Un diagramme nous aidera à visualiser la situation.

    clipboard_ea415f63ad2acc69c7ea17326f1ee0337.png

    Nous remplissons le tableau pour organiser les informations. Nous recherchons la vitesse de course de Jazmine. Let\(r\) = vitesse de course de Jazmine.

    Sa vitesse à vélo est 6 miles plus rapide que sa vitesse de course. \(r + 4\)= sa vitesse de pédalage

    Les distances sont données, saisissez-les dans le graphique. Depuis\(D=r \cdot t\), nous résolvons\(t\) et obtenons\(t=\dfrac{D}{r}\). Nous divisons la distance par le taux de chaque ligne et plaçons l'expression dans la colonne temporelle.

    Tarif :\(\cdot\) temps = distance
    Courir \ (\ cdot \) Temps = distance">\(r\) \(\dfrac{8}{r}\) 8
    vélo \ (\ cdot \) Temps = distance">\(r+4\) \(\dfrac{24}{r+4}\) 24
      \ (\ cdot \) Temps = distance"> 3  

    Écrivez une phrase : Son temps plus le temps qu'elle passe à vélo est de 3 heures.

    Traduisez la phrase pour obtenir l'équation.

    \[\dfrac{8}{r}+\dfrac{24}{r+4}=3 \nonumber \]

    Résoudre.

    \ [\ begin {aligné}
    r (r+4) \ left (\ dfrac {8} {r} + \ dfrac {24} {r+4} \ droite) &=3 \ cdot r (r+4) \ \
    8 (r+4) +24 r &=3 r (r+4) \ \
    8 r+32+24 r &=3 r^ {2} +12 \ r \
    32+32 r &=3 r^ {2} +12 r \ \
    0 &=3 r^ {2} -20 r-32 \ \
    0 & =( 3 r+ 4) (r-8)
     \ end {aligné} \ nonnumber \]

    \[\begin{array}{lc} {(3 r+4)=0} & {(r-8)=0} \\ \cancel{r=\dfrac{4}{3}} \quad & {r=8} \end{array} \nonumber \]

    Vérifiez.

    Une vitesse négative n'a pas de sens dans ce problème, tout\(r=8\) comme la solution.

    Est-ce que 8 mi/h est une vitesse de course raisonnable ? Oui.

    Si le rythme de course de Jazmine est de 4, alors son rythme de cyclisme\(r+4\), qui est\(8+4=12\).

    \[\text { Run } 8 \mathrm{mph} \quad \dfrac{8 \mathrm{miles}}{8 \mathrm{mph}}=1 \text { hour } \nonumber \]

    \[\text { Bike } 12 \text { mph } \quad \dfrac{24 \text { miles }}{12 \mathrm{mph}}=2 \text { hours } \nonumber \]

    \(y=\dfrac{k}{x}\)