7.2 : Multiplier et diviser des expressions rationnelles
- Page ID
- 194437
À la fin de cette section, vous serez en mesure de :
- Déterminer les valeurs pour lesquelles une expression rationnelle n'est pas définie
- Simplifier les expressions
- Multipliez les expressions
- Divisez les expressions
- Multiplier et diviser les fonctions rationnelles
Nous avons déjà examiné les propriétés des fractions et leur fonctionnement. Nous avons introduit des nombres rationnels, qui ne sont que des fractions dont les numérateurs et les dénominateurs sont des nombres entiers. Dans ce chapitre, nous allons travailler avec des fractions dont les numérateurs et les dénominateurs sont des polynômes. Nous appelons ce type d'expression une expression rationnelle.
Une expression rationnelle est une expression de la forme\(\dfrac{p}{q}\), where \(p\) et\(q\) sont des polynômes et\(q\neq 0\).
Voici quelques exemples d'expressions rationnelles :
\[−\dfrac{24}{56} \qquad \dfrac{5x}{12y} \qquad \dfrac{4x+1}{x^2−9} \qquad \dfrac{4x^2+3x−1}{2x−8}\nonumber\]
Notez que la première expression rationnelle répertoriée ci-dessus,\(−\dfrac{24}{56}\), n'est qu'une fraction. Comme une constante est un polynôme de degré zéro, le rapport de deux constantes est une expression rationnelle, à condition que le dénominateur ne soit pas nul.
Nous allons effectuer les mêmes opérations avec des expressions rationnelles que nous avons fait avec des fractions. Nous allons les simplifier, les ajouter, les soustraire, les multiplier, les diviser et les utiliser dans des applications.
Déterminer les valeurs pour lesquelles une expression rationnelle n'est pas définie
Si le dénominateur est zéro, l'expression rationnelle n'est pas définie. Le numérateur d'une expression rationnelle peut être 0, mais pas le dénominateur.
Lorsque nous travaillons avec une fraction numérique, il est facile d'éviter de diviser par zéro car nous pouvons voir le nombre dans le dénominateur. Afin d'éviter de diviser par zéro dans une expression rationnelle, nous ne devons pas autoriser les valeurs de la variable qui feront du dénominateur zéro.
Donc, avant de commencer une opération avec une expression rationnelle, nous l'examinons d'abord pour trouver les valeurs qui rendraient le dénominateur zéro. Ainsi, lorsque nous résolvons une équation rationnelle par exemple, nous saurons si les solutions algébriques que nous trouvons sont autorisées ou non.
- Réglez le dénominateur à zéro.
- Résolvez l'équation.
Déterminez la valeur pour laquelle chaque expression rationnelle n'est pas définie :
a.\(\dfrac{8a^2b}{3c}\) b.\(\dfrac{4b−3}{2b+5}\)\(\dfrac{x+4}{x^2+5x+6}\) c.
Solution
L'expression ne sera pas définie lorsque le dénominateur est zéro.
un.
\(\begin{array} {ll} &\dfrac{8a^2b}{3c} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve} \\ \text{for the variable.} \end{array} &3c=0 \\ &c=0 \\ &\dfrac{8a^2b}{3c}\text{ is undefined for }c=0 \end{array} \)
b.
\(\begin{array} {ll} &\dfrac{4b-3}{2b+5} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve} \\ \text{for the variable.} \end{array} &2b+5=0 \\ &2b=-5 \\ &b=-\dfrac{5}{2} \\ & \\ &\dfrac{4b-3}{2b+5} \text{ is undefined for }b=-\dfrac{5}{2} \end{array} \)
c.
\(\begin{array} {ll} &\dfrac{x+4}{x^2 + 5x + 6} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve } \\ \text{for the variable.} \end{array} &x^2+5x+6=0 \\ &(x+2)(x+3)=0 \\ &x+2=0\text{ or }x+3=0 \\ &x=-2\text{ or }x=-3 \\ & \\ &\dfrac{x+4}{x^2+5x+6}\text{ is undefined for }x=-2\text{ or }x=-3 \end{array} \)
Déterminez la valeur pour laquelle chaque expression rationnelle n'est pas définie.
a.\(\dfrac{3y^2}{8x}\) b.\(\dfrac{8n−5}{3n+1}\) c.\(\dfrac{a+10}{a^2+4a+3}\)
- Réponse
-
a.\(x=0\)
b.\(n=−\dfrac{1}{3}\)
c.\(a=−1,a=−3\)
Déterminez la valeur pour laquelle chaque expression rationnelle n'est pas définie.
a.\(\dfrac{4p}{5q}\) b.\(\dfrac{y−1}{3y+2}\) c.\(\dfrac{m−5}{m^2+m−6}\)
- Réponse
-
a.\(q=0\)
b.\(y=−\dfrac{2}{3}\)
c.\(m=2,m=−3\)
Simplifier les expressions
Une fraction est considérée comme simplifiée s'il n'existe aucun facteur commun, autre que 1, dans son numérateur et son dénominateur. De même, une expression rationnelle simplifiée n'a aucun facteur commun, autre que 1, dans son numérateur et son dénominateur.
Une expression rationnelle est considérée comme simplifiée s'il n'y a pas de facteurs communs dans son numérateur et son dénominateur.
Par exemple,
\[ \begin{array} {l} \dfrac{x+2}{x+3} \text{ is simplified because there are no common factors of } x+2 \text{ and }x+3. \\ \dfrac{2x}{3x} \text{ is not simplified because x is a common factor of }2x\text{ and }3x. \\ \end{array} \nonumber\]
Nous utilisons la propriété Fractions équivalentes pour simplifier les fractions numériques. Nous le reformulons ici car nous l'utiliserons également pour simplifier les expressions rationnelles.
Si\(a\)\(b\), et\(c\) sont des nombres où\(b\neq 0,c\neq 0,\)
\[\text {then } \dfrac{a}{b}=\dfrac{a·c}{b·c} \text{ and } \dfrac{a·c}{b·c}=\dfrac{a}{b}\nonumber\]
Notez que dans la propriété Fractions équivalentes, les valeurs qui rendraient les dénominateurs nuls sont spécifiquement interdites. Nous voyons\(b\neq 0,c\neq 0\) clairement ce qui est indiqué.
Pour simplifier les expressions rationnelles, nous écrivons d'abord le numérateur et le dénominateur sous forme factorielle. Nous supprimons ensuite les facteurs communs à l'aide de la propriété des fractions équivalentes.
Soyez très prudent lorsque vous supprimez les facteurs courants. Les facteurs sont multipliés pour fabriquer un produit. Vous pouvez supprimer un facteur d'un produit. Vous ne pouvez pas supprimer un terme d'une somme.

Supprimer les\(x\) « de\(\dfrac{x+5}{x}\) » reviendrait à annuler les «\(2\) » de la fraction\(\dfrac{2+5}{2}!\)
Comment simplifier une expression rationnelle
Simplifiez :\(\dfrac{x^2+5x+6}{x^2+8x+12}\)
Solution
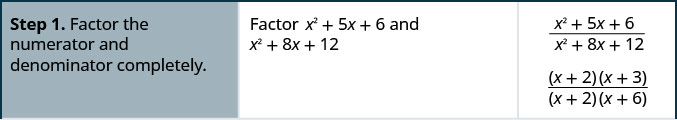

Simplifiez :\(\dfrac{x^2−x−2}{x^2−3x+2}\).
- Réponse
-
\(\dfrac{x+1}{x−1},x\neq 2,x\neq 1\)
Simplifiez :\(\dfrac{x^2−3x−10}{x^2+x−2}\).
- Réponse
-
\(\dfrac{x−5}{x−1},x\neq −2,x\neq 1\)
Nous résumons maintenant les étapes à suivre pour simplifier les expressions rationnelles.
- Facturez complètement le numérateur et le dénominateur.
- Simplifiez en divisant les facteurs communs.
Habituellement, nous laissons l'expression rationnelle simplifiée sous forme factorielle. De cette façon, il est facile de vérifier que nous avons supprimé tous les facteurs communs.
Nous utiliserons les méthodes que nous avons apprises pour factoriser les polynômes dans les numérateurs et les dénominateurs dans les exemples suivants.
Chaque fois que nous écrivons une expression rationnelle, nous devons faire une déclaration interdisant les valeurs qui donneraient un dénominateur zéro. Cependant, pour nous concentrer sur le travail à accomplir, nous omettrons de l'écrire dans les exemples.
Simplifiez :\(\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2}\).
Solution
\(\begin{array} {ll} &\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2} \\ & \\ & \\ \begin{array} {l} \text{Factor the numerator and denominator,} \\ \text{first factoring out the GCF.} \end{array} &\dfrac{3(a^2−4ab+4b^2)}{6(a^2−4b^2)} \\ & \\ &\dfrac{3(a−2b)(a−2b)}{6(a+2b)(a−2b)} \\ & \\ \text{Remove the common factors of }a−2b\text{ and }3. &\dfrac{\cancel{3}(a−2b)\cancel{(a−2b)}}{\cancel{3}·2(a+2b)\cancel{(a−2b)}} \\ &\dfrac{a−2b}{2(a+2b)} \end{array} \)
Simplifiez :\(\dfrac{2x^2−12xy+18y^2}{3x^2−27y^2}\).
- Réponse
-
\(\dfrac{2(x−3y)}{3(x+3y)}\)
Simplifiez :\(\dfrac{5x^2−30xy+25y^2}{2x^2−50y^2}\).
- Réponse
-
\(\dfrac{5(x−y)}{2(x+5y)}\)
Nous allons maintenant voir comment simplifier une expression rationnelle dont le numérateur et le dénominateur ont des facteurs opposés. Nous avons déjà introduit la notation opposée : le contraire de\(a\) est\(−a\) et\(−a=−1·a\).
La fraction numérique, disons, se\(\dfrac{7}{−7}\) simplifie à\(−1\). Nous reconnaissons également que le numérateur et le dénominateur sont opposés.
La fraction\(\dfrac{a}{−a}\), dont le numérateur et le dénominateur sont opposés, se simplifie également en\(−1\).
\[\begin{array} {ll} \text{Let’s look at the expression }b−a. &b−a \\ \text{Rewrite.} &−a+b \\ \text{Factor out }–1. &−1(a−b) \nonumber\end{array} \]
Cela nous indique que\(b−a\) c'est le contraire de\(a−b\).
En général, on pourrait écrire le contraire de\(a−b\) as\(b−a\). Ainsi, l'expression rationnelle se\(\dfrac{a−b}{b−a}\) simplifie en\(−1\).
Le contraire de l'\(a−b\)est\(b−a\).
\[\dfrac{a−b}{b−a}=−1 \quad a\neq b\nonumber\]
Une expression et son opposé se divisent en\(−1\).
Nous utiliserons cette propriété pour simplifier les expressions rationnelles qui contiennent des contraires dans leurs numérateurs et dénominateurs. Veillez à ne pas traiter\(a+b\) et à ne pas les traiter\(b+a\) comme des contraires. Rappelons qu'en plus, l'ordre n'a pas d'importance\(a+b=b+a\). Donc si\(a\neq −b\), alors\(\dfrac{a+b}{b+a}=1\).
Simplifiez :\(\dfrac{x^2−4x−32}{64−x^2}\)
Solution
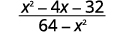 |
|
| Facturez le numérateur et le dénominateur. | 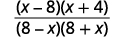 |
| Reconnaissez les facteurs opposés. | 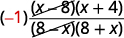 |
| Simplifiez. | 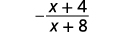 |
Simplifiez :\(\dfrac{x^2−4x−5}{25−x^2}\)
- Réponse
-
\(−\dfrac{x+1}{x+5}\)
Simplifiez :\(\dfrac{x^2+x−2}{1−x^2}\).
- Réponse
-
\(−\dfrac{x+2}{x+1}\)
Multipliez les expressions
Pour multiplier les expressions rationnelles, nous faisons exactement ce que nous avons fait avec des fractions numériques. Nous multiplions les numérateurs et multiplions les dénominateurs. Ensuite, s'il existe des facteurs communs, nous les supprimons pour simplifier le résultat.
Si\(p\),\(q\)\(r\), et\(s\) sont des polynômes où\(q\neq 0\),\(s\neq 0\), alors
\[\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\nonumber\]
Pour multiplier les expressions rationnelles, multipliez les numérateurs et multipliez les dénominateurs.
N'oubliez pas que tout au long de ce chapitre, nous supposerons que toutes les valeurs numériques qui donneraient au dénominateur zéro sont exclues. Nous n'écrirons pas les restrictions pour chaque expression rationnelle, mais gardez à l'esprit que le dénominateur ne peut jamais être zéro. Donc, dans l'exemple suivant\(x\neq 0\),\(x\neq 3\), et\(x\neq 4.\)
Simplifiez :\(\dfrac{2x}{x^2−7x+12}·\dfrac{x^2−9}{6x^2}\).
Solution
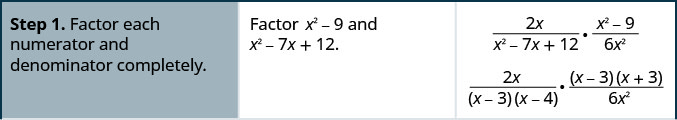


Simplifiez :\(\dfrac{5x}{x^2+5x+6}·\dfrac{x^2−4}{10x}\).
- Réponse
-
\(\dfrac{x−2}{2(x+3)}\)
Simplifiez :\(\dfrac{9x^2}{x^2+11x+30}·\dfrac{x^2−36}{3x^2}\).
- Réponse
-
\(\dfrac{3(x−6)}{x+5}\)
- Facturez complètement chaque numérateur et dénominateur.
- Multipliez les numérateurs et les dénominateurs.
- Simplifiez en divisant les facteurs communs.
Multipliez :\(\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5}\).
Solution
\(\begin{array} {ll} &\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5} \\ & \\ \begin{array} {ll} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &\dfrac{(3a+1)(a−3)(a+5)(a+5)}{(a−5)(a+5)(3a+1)(a−5)} \\ & \\ \begin{array} {l} \text{Simplify by dividing out} \\ \text{common factors.} \end{array} &\dfrac{\cancel{(3a+1)}(a−3)\cancel{(a+5)}(a+5)}{(a−5)\cancel{(a+5)}\cancel{(3a+1)}(a−5)} \\ & \\ \text{Simplify.} &\dfrac{(a−3)(a+5)}{(a−5)(a−5)} \\ & \\ \text{Rewrite }(a−5)(a−5)\text{ using an exponent.} &\dfrac{(a−3)(a+5)}{(a−5)^2} \end{array}\)
Simplifiez :\(\dfrac{2x^2+5x−12}{x^2−16}·\dfrac{x^2−8x+16}{2x^2−13x+15}\).
- Réponse
-
\(\dfrac{x−4}{x−5}\)
Simplifiez :\(\dfrac{4b^2+7b−2}{1−b^2}·\dfrac{b^2−2b+1}{4b^2+15b−4}\).
- Réponse
-
\(−\dfrac{(b+2)(b−1)}{(1+b)(b+4)}\)
Divisez les expressions
Comme nous l'avons fait pour les fractions numériques, pour diviser les expressions rationnelles, nous multiplions la première fraction par l'inverse de la seconde.
Si\(p\),\(q\)\(r\), et\(s\) sont des polynômes où\(q\neq 0\),\(r\neq 0\),\(s\neq 0\), alors
\[\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\nonumber\]
Pour diviser des expressions rationnelles, multipliez la première fraction par l'inverse de la seconde.
Une fois que nous avons réécrit la division sous forme de multiplication de la première expression par l'inverse de la seconde, nous factorisons tout et recherchons des facteurs communs.
Diviser :\(\dfrac{p^3+q^3}{2p^2+2pq+2q^2}÷\dfrac{p^2−q^2}{6}\).
Solution




Simplifiez :\(\dfrac{x^3−8}{3x^2−6x+12}÷\dfrac{x^2-4}{6}\).
- Réponse
-
\(\dfrac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
Simplifiez :\(\dfrac{2z^2}{z^2−1}÷\dfrac{z^3−z^2+z}{z^3+1}\).
- Réponse
-
\(\dfrac{2z}{z−1}\)
- Réécrivez la division comme le produit de la première expression rationnelle et de l'inverse de la seconde.
- Facturez complètement les numérateurs et les dénominateurs.
- Multipliez les numérateurs et les dénominateurs ensemble.
- Simplifiez en divisant les facteurs communs.
Rappelons d'après Utiliser le langage de l'algèbre qu'une fraction complexe est une fraction qui contient une fraction dans le numérateur, le dénominateur ou les deux. N'oubliez pas non plus qu'une barre de fraction signifie division. Une fraction complexe est une autre façon d'écrire la division de deux fractions.
Diviser :\(\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}}\).
Solution
\(\begin{array} {ll} &\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}} \\ & \\ \text{Rewrite with a division sign.} &\dfrac{6x^2−7x+2}{4x−8}÷\dfrac{2x^2−7x+3}{x^2−5x+6} \\ & \\ \begin{array} {l} \text{Rewrite as product of first times reciprocal} \\ \text{of second.} \end{array} &\dfrac{6x^2−7x+2}{4x−8}·\dfrac{x^2−5x+6}{2x^2−7x+3} \\ & \\ \begin{array} {l} \text{Factor the numerators and the} \\ \text{denominators, and then multiply.} \end{array} &\dfrac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)} \\ & \\ \text{Simplify by dividing out common factors.} &\dfrac{\cancel{(2x−1)}(3x−2)\cancel{(x−2)}\cancel{(x−3)}}{4\cancel{(x−2)}\cancel{(2x−1)}\cancel{(x−3)}} \\ \text{Simplify.} &\dfrac{3x−2}{4} \end{array}\)
Simplifiez :\(\dfrac{\dfrac{3x^2+7x+2}{4x+24}}{\dfrac{3x^2−14x−5}{x^2+x−30}}\).
- Réponse
-
\(\dfrac{x+2}{4}\)
Simplifiez :\(\dfrac{\dfrac{y^2−36}{2y^2+11y−6}}{\dfrac{2y^2−2y−60}{8y−4}}\).
- Réponse
-
\(\dfrac{2}{y+5}\)
Si nous avons plus de deux expressions rationnelles avec lesquelles travailler, nous suivons toujours la même procédure. La première étape sera de réécrire toute division sous forme de multiplication par l'inverse. Ensuite, nous factorisons et multiplions.
Effectuez les opérations indiquées :\(\dfrac{3x−6}{4x−4}·\dfrac{x^2+2x−3}{x^2−3x−10}÷\dfrac{2x+12}{8x+16}\)
Solution
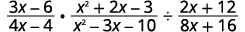 |
|
| Réécrivez la division sous forme de multiplication par l'inverse. |
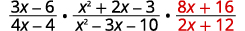 |
| Facturez les numérateurs et les dénominateurs. | 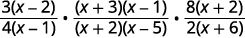 |
| Multipliez les fractions. Mettre les constantes au premier plan aidera à éliminer les facteurs communs. |
|
| Simplifiez en divisant les facteurs communs. | 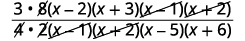 |
| Simplifiez. | 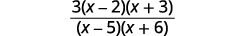 |
Effectuez les opérations indiquées :\(\dfrac{4m+4}{3m−15}·\dfrac{m^2−3m−10}{m^2−4m−32}÷\dfrac{12m−36}{6m−48}\)
- Réponse
-
\(\dfrac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
Effectuez les opérations indiquées :\(\dfrac{2n^2+10n}{n−1}÷\dfrac{n^2+10n+24}{n^2+8n−9}·\dfrac{n+4}{8n^2+12n}\)
- Réponse
-
\(\dfrac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
Multiplier et diviser les fonctions rationnelles
Nous avons commencé cette section en indiquant qu'une expression rationnelle est une expression de la forme\(\dfrac{p}{q}\), où p et q sont des polynômes et\(q\neq 0\). De même, nous définissons une fonction rationnelle comme une fonction de la forme\(R(x)=\dfrac{p(x)}{q(x)}\) où\(p(x)\) et\(q(x)\) sont des fonctions polynomiales et n'\(q(x)\)est pas nulle.
Une fonction rationnelle est fonction de la forme
\[R(x)=\dfrac{p(x)}{q(x)}\nonumber\]
où\(p(x)\) et\(q(x)\) sont des fonctions polynomiales et n'\(q(x)\)est pas nul.
Le domaine d'une fonction rationnelle est composé de tous les nombres réels, à l'exception des valeurs qui entraîneraient une division par zéro. Nous devons éliminer toutes les valeurs qui font\(q(x)=0\).
- Réglez le dénominateur à zéro.
- Résolvez l'équation.
- Le domaine comprend tous les nombres réels à l'exception des valeurs trouvées à l'étape 2.
Trouvez le domaine de\(R(x)=\dfrac{2x^2−14x}{4x^2−16x−48}\).
Solution
Le domaine sera composé uniquement de nombres réels, à l'exception des valeurs qui font du dénominateur zéro. Nous allons fixer le dénominateur à zéro, résoudre cette équation, puis exclure ces valeurs du domaine.
\(\begin{array} {ll} \text{Set the denominator to zero.} &4x^2−16x−48=0 \\ \text{Factor, first factor out the GCF.} &4(x^2−4x−12)=0 \\ &4(x−6)(x+2)=0 \\ \text{Use the Zero Product Property.} &4\neq 0\quad x−6=0\quad x+2=0 \\ \text{Solve.} &\hspace{24mm}x=6\qquad x=−2 \\ &\text{The domain of }R(x)\text{ is all real numbers} \\ &\text{where }x\neq 6\text{ and }x\neq −2 \end{array}\).
Trouvez le domaine de\(R(x)=\dfrac{2x^2−10x}{4x^2−16x−20}\).
- Réponse
-
Le domaine de\(R(x)\) est composé de tous les nombres réels où\(x\neq 5\) et\(x\neq −1\).
Trouvez le domaine de\(R(x)=\dfrac{4x^2−16x}{8x^2−16x−64}\).
- Réponse
-
Le domaine de\(R(x)\) est composé de tous les nombres réels où\(x\neq 4\) et\(x\neq −2\).
Pour multiplier les fonctions rationnelles, nous multiplions les expressions rationnelles qui en résultent sur le côté droit de l'équation en utilisant les mêmes techniques que celles que nous avons utilisées pour multiplier les expressions rationnelles.
Trouvez\(R(x)=f(x)·g(x)\) où\(f(x)=\dfrac{2x−6}{x^2−8x+15}\) et\(g(x)=\dfrac{x^2−25}{2x+10}\).
Solution
\(\begin{array} {ll} &R(x)=f(x)·g(x) \\ & \\ &R(x)=\dfrac{2x−6}{x^2−8x+15}·\dfrac{x^2−25}{2x+10} \\ & \\ \text{Factor each numerator and denominator.} &R(x)=\dfrac{2(x−3)}{(x−3)(x−5)}·\dfrac{(x−5)(x+5)}{2(x+5)} \\ & \\ \text{Multiply the numerators and denominators.} &R(x)=\dfrac{2(x−3)(x−5)(x+5)}{2(x−3)(x−5)(x+5)} \\ & \\ \text{Remove common factors.} &R(x)=\dfrac{\cancel{2}\cancel{(x−3)}\cancel{(x−5)}\cancel{(x+5)}}{\cancel{2}\cancel{(x−3)}\cancel{(x−5)}\cancel{(x+5)}} \\ & \\ \text{Simplify.} &R(x)=1 \end{array}\)
Trouvez\(R(x)=f(x)·g(x)\) où\(f(x)=\dfrac{3x−21}{x^2−9x+14}\) et\(g(x)=\dfrac{2x^2−8}{3x+6}\).
- Réponse
-
\(R(x)=2\)
Trouvez\(R(x)=f(x)·g(x)\) où\(f(x)=\dfrac{x^2−x}{3x^2+27x−30}\) et\(g(x)=\dfrac{x^2−100}{x^2−10x}\).
- Réponse
-
\(R(x)=\dfrac{1}{3}\)
Pour diviser les fonctions rationnelles, nous divisons les expressions rationnelles qui en résultent sur le côté droit de l'équation en utilisant les mêmes techniques que celles que nous avons utilisées pour diviser les expressions rationnelles.
Trouvez\(R(x)=\dfrac{f(x)}{g(x)}\) où\(f(x)=\dfrac{3x^2}{x^2−4x}\) et\(g(x)=\dfrac{9x^2−45x}{x^2−7x+10}\).
Solution
\(\begin{array} {ll} &R(x)=\dfrac{f(x)}{g(x)} \\ \text{Substitute in the functions }f(x),\space g(x). &R(x)=\dfrac{\dfrac{3x^2}{x^2−4x}}{\dfrac{9x^2−45x}{x^2−7x+10}} \\ & \\ \begin{array} {l} \text{Rewrite the division as the product of} \\ f(x)\text{ and the reciprocal of }g(x). \end{array} &R(x)=\dfrac{3x^2}{x^2−4x}·\dfrac{x^2−7x+10}{9x^2−45x} \\ & \\ \begin{array} {l} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &R(x)=\dfrac{3·x·x·(x−5)(x−2)}{x(x−4)·3·3·x·(x−5)} \\ & \\ \text{Simplify by dividing out common factors.} &R(x)=\dfrac{\cancel{3}·\cancel{x}·\cancel{x}\cancel{(x−5)}(x−2)}{\cancel{x}(x−4)·\cancel{3}·3·\cancel{x}\cancel{(x−5)}} \\ & \\ &R(x)=\dfrac{x−2}{3(x−4)} \end{array}\)
Trouvez\(R(x)=\dfrac{f(x)}{g(x)}\) où\(f(x)=\dfrac{2x^2}{x^2−8x}\) et\(g(x)=\dfrac{8x^2+24x}{x^2+x−6}\).
- Réponse
-
\(R(x)=\dfrac{x−2}{4(x−8)}\)
Trouvez\(R(x)=\dfrac{f(x)}{g(x)}\) où\(f(x)=\dfrac{15x^2}{3x^2+33x}\) et\(g(x)=\dfrac{5x−5}{x^2+9x−22}\).
- Réponse
-
\(R(x)=\dfrac{x(x−2)}{x−1}\)
Concepts clés
- Déterminez les valeurs pour lesquelles une expression rationnelle n'est pas définie.
- Réglez le dénominateur à zéro.
- Résolvez l'équation.
- Propriété des fractions équivalentes
Si\(a\)\(b\), et\(c\) sont des nombres où\(b\neq 0\)\(c\neq 0\), alors
\(\quad\dfrac{a}{b}=\dfrac{a·c}{b·c}\) et\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\) - Comment simplifier une expression rationnelle.
- Facturez complètement le numérateur et le dénominateur.
- Simplifiez en divisant les facteurs communs.
- Les contraires dans une expression rationnelle
Le contraire de l'\(a−b\)est\(b−a\).
\(\quad\dfrac{a−b}{b−a}=−1 \qquad a\neq b\)
Une expression et son opposé se divisent en\(−1\). - Multiplication des expressions rationnelles
Si\(p\)\(q\)\(r\),, et\(s\) sont des polynômes où\(q\neq 0\)\(s\neq 0\), alors
\(\quad\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\) - Comment multiplier les expressions rationnelles.
- Facturez complètement chaque numérateur et dénominateur.
- Multipliez les numérateurs et les dénominateurs.
- Simplifiez en divisant les facteurs communs.
- Division des expressions rationnelles
Si\(p\)\(q\),\(r\), et\(s\) sont des polynômes où\(q\neq 0\),\(r\neq 0\),\(s\neq 0\), alors
\(\quad\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\) - Comment diviser les expressions rationnelles.
- Réécrivez la division comme le produit de la première expression rationnelle et de l'inverse de la seconde.
- Facturez complètement les numérateurs et les dénominateurs.
- Multipliez les numérateurs et les dénominateurs ensemble.
- Simplifiez en divisant les facteurs communs.
- Comment déterminer le domaine d'une fonction rationnelle.
- Réglez le dénominateur à zéro.
- Résolvez l'équation.
- Le domaine comprend tous les nombres réels à l'exception des valeurs trouvées à l'étape 2.
Lexique
- expression rationnelle
- Une expression rationnelle est une expression de la forme\(\dfrac{p}{q}\), où\(p\) et\(q\) sont des polynômes et\(q\neq 0\).
- expression rationnelle simplifiée
- Une expression rationnelle simplifiée n'a aucun facteur commun\(1\), à part son numérateur et son dénominateur.
- fonction rationnelle
- Une fonction rationnelle est une fonction de la forme\(R(x)=\dfrac{p(x)}{q(x)}\) où\(p(x)\) et\(q(x)\) sont des fonctions polynomiales et n'\(q(x)\)est pas nulle.


