6.2 : Plus grand facteur commun et facteur par groupe
- Page ID
- 194230
À la fin de cette section, vous serez en mesure de :
- Trouvez le plus grand facteur commun entre deux expressions ou plus
- Facteur : le plus grand facteur commun d'un polynôme
- Facteur par regroupement
Avant de commencer, répondez à ce questionnaire de préparation.
Trouvez le plus grand facteur commun entre deux expressions ou plus
Auparavant, nous avons multiplié les facteurs ensemble pour obtenir un produit. Maintenant, nous allons inverser ce processus ; nous allons commencer par un produit, puis le décomposer en plusieurs facteurs. La division d'un produit en facteurs s'appelle l'affacturage.
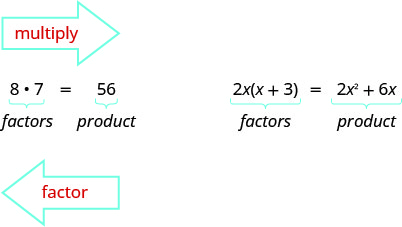
Nous avons appris à factoriser les nombres pour trouver le multiple le moins commun (LCM) de deux nombres ou plus. Nous allons maintenant factoriser les expressions et trouver le plus grand facteur commun entre deux expressions ou plus. La méthode que nous utilisons est similaire à celle que nous avons utilisée pour trouver le LCM.
Le plus grand facteur commun (GCF) de deux expressions ou plus est la plus grande expression qui est un facteur parmi toutes les expressions.
Nous résumons les étapes que nous utilisons pour trouver le plus grand facteur commun.
- Facturez chaque coefficient en nombres premiers. Écrivez toutes les variables avec des exposants sous forme développée.
- Répertorie tous les facteurs qui correspondent aux facteurs communs dans une colonne. Dans chaque colonne, encerclez les facteurs communs.
- Déterminez les facteurs communs à toutes les expressions.
- Multipliez les facteurs.
L'exemple suivant nous montrera les étapes à suivre pour trouver le plus grand facteur commun entre trois expressions.
Trouvez le plus grand facteur commun de\(21x^3,\space 9x^2,\space 15x\).
- Réponse
-
Facteur chaque coefficient en nombres premiers et écris les variables avec les exposants sous forme développée. Encerclez les facteurs communs dans chaque colonne. Abaissez les facteurs communs. 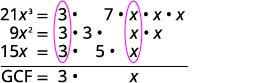
Multipliez les facteurs. GCF\(=3x\) Le GCF de\(21x^3\),\(9x^2\) et\(15x\) est\(3x\).
Trouvez le plus grand facteur commun :\(25m^4,\space 35m^3,\space 20m^2.\)
- Réponse
-
\(5m^2\)
Trouvez le plus grand facteur commun :\(14x^3,\space 70x^2,\space 105x\).
- Réponse
-
\(7x\)
Facteur : le plus grand facteur commun à partir d'un polynôme
Il est parfois utile de représenter un nombre comme le produit de facteurs, par exemple, 12 sous forme de\(2·6\) ou\(3·4\). En algèbre, il peut également être utile de représenter un polynôme sous forme factorielle. Nous allons commencer par un produit, tel que\(3x^2+15x\), et terminer par ses facteurs\(3x(x+5)\). Pour ce faire, nous appliquons la propriété distributive « à l'envers ».
Nous énonçons ici la propriété distributive telle que vous l'avez vue dans les chapitres précédents et « à l'envers ».
Si a, b et c sont des nombres réels, alors
\[a(b+c)=ab+ac \quad \text{and} \quad ab+ac=a(b+c)\nonumber\]
Le formulaire de gauche est utilisé pour multiplier. Le formulaire de droite est utilisé pour factoriser.
Alors, comment utilisez-vous la propriété distributive pour factoriser un polynôme ? Il vous suffit de trouver le GCF de tous les termes et d'écrire le polynôme sous forme de produit !
Facteur :\(8m^3−12m^2n+20mn^2\).
- Réponse
-




Facteur :\(9xy^2+6x^2y^2+21y^3\).
- Réponse
-
\(3y^2(3x+2x^2+7y)\)
Facteur :\(3p^3−6p^2q+9pq^3\).
- Réponse
-
\(3p(p^2−2pq+3q^3)\)
- Détermine le GCF de tous les termes du polynôme.
- Réécrivez chaque terme en tant que produit à l'aide du GCF.
- Utilisez la propriété distributive « inverse » pour factoriser l'expression.
- Vérifiez en multipliant les facteurs.
Nous utilisons le terme « facteur » à la fois comme nom et comme verbe :
\[\begin{array} {ll} \text{Noun:} &\hspace{50mm} 7 \text{ is a factor of }14 \\ \text{Verb:} &\hspace{50mm} \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
Facteur :\(5x^3−25x^2\).
- Réponse
-
Trouvez le GCF de\(5x^3\) et\(25x^2\). 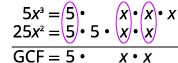
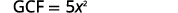
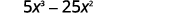
Réécrivez chaque terme. 
Tenez compte du GCF. 
Vérifiez :
\[5x^2(x−5) \nonumber\]\[5x^2·x−5x^2·5 \nonumber\]
\[5x^3−25x^2 \checkmark\nonumber\]
Facteur :\(2x^3+12x^2\).
- Réponse
-
\(2x^2(x+6)\)
Facteur :\(6y^3−15y^2\).
- Réponse
-
\(3y^2(2y−5)\)
Facteur :\(8x^3y−10x^2y^2+12xy^3\).
- Réponse
-
Le GCF de\(8x^3y,\space −10x^2y^2,\) et\(12xy^3\)
est\(2xy\).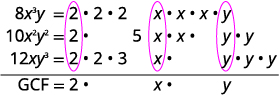

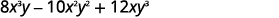
Réécrivez chaque terme en utilisant le GCF,\(2xy\). 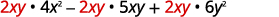
Tenez compte du GCF. 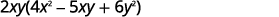
Vérifiez :
\[2xy(4x^2−5xy+6y^2)\nonumber\]\[2xy·4x^2−2xy·5xy+2xy·6y^2\nonumber\]
\[8x^3y−10x^2y^2+12xy^3\checkmark\nonumber\]
Facteur :\(15x^3y−3x^2y^2+6xy^3\).
- Réponse
-
\(3xy(5x^2−xy+2y^2)\)
Facteur :\(8a^3b+2a^2b^2−6ab^3\).
- Réponse
-
\(2ab(4a^2+ab−3b^2)\)
Lorsque le coefficient principal est négatif, nous déduisons le négatif dans le cadre du GCF.
Facteur :\(−4a^3+36a^2−8a\).
- Réponse
-
Le coefficient principal étant négatif, le GCF sera négatif.
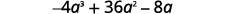
Réécrivez chaque terme en utilisant le GCF,\(−4a\). 
Tenez compte du GCF. 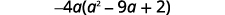
Vérifiez :
\[−4a(a^2−9a+2)\nonumber\]\[−4a·a^2−(−4a)·9a+(−4a)·2\nonumber\]
\[−4a^3+36a^2−8a\checkmark\nonumber\]
Facteur :\(−4b^3+16b^2−8b\).
- Réponse
-
\(−4b(b^2−4b+2)\)
Facteur :\(−7a^3+21a^2−14a\).
- Réponse
-
\(−7a(a^2−3a+2)\)
Jusqu'à présent, nos principaux facteurs communs ont été les monomiaux. Dans l'exemple suivant, le plus grand facteur commun est un binôme.
Facteur :\(3y(y+7)−4(y+7)\).
- Réponse
-
Le GCF est le binôme\(y+7\).
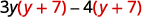
Tenez compte du GCF,\((y+7)\). \((y+7)(3 y-4)\) Vérifiez vous-même en multipliant.
Facteur :\(4m(m+3)−7(m+3)\).
- Réponse
-
\((m+3)(4m−7)\)
Facteur :\(8n(n−4)+5(n−4)\).
- Réponse
-
\((n−4)(8n+5)\)
Facteur par regroupement
Parfois, il n'y a pas de facteur commun à tous les termes d'un polynôme. Lorsqu'il y a quatre termes, nous séparons le polynôme en deux parties avec deux termes dans chaque partie. Recherchez ensuite le GCF dans chaque partie. Si le polynôme peut être factorisé, vous constaterez qu'un facteur commun émerge des deux parties. Tous les polynômes ne peuvent pas être pris en compte. Tout comme certains nombres sont premiers, certains polynômes sont premiers.
Facteur par regroupement :\(xy+3y+2x+6\).
- Réponse
-




Facteur par regroupement :\(xy+8y+3x+24\).
- Réponse
-
\((x+8)(y+3)\)
Facteur par regroupement :\(ab+7b+8a+56\).
- Réponse
-
\((a+7)(b+8)\)
- Termes de groupe ayant des facteurs communs.
- Déterminez le facteur commun à chaque groupe.
- Facturez le facteur commun à partir de l'expression.
- Vérifiez en multipliant les facteurs.
Facteur par regroupement : ⓐ\(x^2+3x−2x−6\) ⓑ\(6x^2−3x−4x+2\).
- Réponse
-
ⓐ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &x^2+3x−2x−6 \\ \text{Separate into two parts.} &x^2+3x\quad −2x−6 \\ \begin{array} {l} \text{Factor the GCF from both parts. Be careful} \\ \text{with the signs when factoring the GCF from} \\ \text{the last two terms.} \end{array} &x(x+3)−2(x+3) \\ \text{Factor out the common factor.} &(x+3)(x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
ⓑ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &6x^2−3x−4x+2 \\ \text{Separate into two parts.} &6x^2−3x\quad −4x+2\\ \text{Factor the GCF from both parts.} &3x(2x−1)−2(2x−1) \\ \text{Factor out the common factor.} &(2x−1)(3x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
Facteur par regroupement : ⓐ\(x^2+2x−5x−10\) ⓑ\(20x^2−16x−15x+12\).
- Réponse
-
ⓐ\((x−5)(x+2)\)
ⓑ\((5x−4)(4x−3)\)
Facteur par regroupement : ⓐ\(y^2+4y−7y−28\) ⓑ\(42m^2−18m−35m+15\).
- Réponse
-
ⓐ\((y+4)(y−7)\)
ⓑ\((7m−3)(6m−5)\)
Concepts clés
- Comment trouver le plus grand facteur commun (GCF) de deux expressions.
- Facturez chaque coefficient en nombres premiers. Écrivez toutes les variables avec des exposants sous forme développée.
- Répertorie tous les facteurs qui correspondent aux facteurs communs dans une colonne. Dans chaque colonne, encerclez les facteurs communs.
- Déterminez les facteurs communs à toutes les expressions.
- Multipliez les facteurs.
- Propriété distributive : Si\(a\)\(b\) et\(c\) sont des nombres réels, alors
\[a(b+c)=ab+ac\quad \text{and}\quad ab+ac=a(b+c)\nonumber\]
Le formulaire de gauche est utilisé pour multiplier. Le formulaire de droite est utilisé pour factoriser. - Comment factoriser le plus grand facteur commun à partir d'un polynôme.
- Détermine le GCF de tous les termes du polynôme.
- Réécrivez chaque terme en tant que produit à l'aide du GCF.
- Utilisez la propriété distributive « inverse » pour factoriser l'expression.
- Vérifiez en multipliant les facteurs.
- Facteur en tant que nom et verbe : Nous utilisons le « facteur » à la fois comme nom et comme verbe.
\[\begin{array} {ll} \text{Noun:} &\quad 7 \text{ is a factor of } 14\\ \text{Verb:} &\quad \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
- Comment factoriser par regroupement.
- Termes de groupe ayant des facteurs communs.
- Déterminez le facteur commun à chaque groupe.
- Facturez le facteur commun à partir de l'expression.
- Vérifiez en multipliant les facteurs.
Lexique
- affacturage
- La division d'un produit en facteurs s'appelle l'affacturage.
- plus grand facteur commun
- Le plus grand facteur commun (GCF) de deux expressions ou plus est la plus grande expression qui est un facteur parmi toutes les expressions.


