Skip to main content
Global

5.5E : Exercices

  1. Last updated
  2. Save as PDF
  • Page ID
    194204

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La pratique rend la perfection

    Diviser les monômes

    Dans les exercices suivants, divisez les monômes.

    1. \(15r^4s^9÷(15r^4s^9)\)

    2. \(20m^8n^4÷(30m^5n^9)\)

    Réponse

    \(\dfrac{2m^3}{3n^5}\)

    3. \(\dfrac{18a^4b^8}{−27a^9b^5}\)

    4. \(\dfrac{45x^5y^9}{−60x^8y^6}\)

    Réponse

    \(\dfrac{−3y^3}{4x^3}\)

    5. \(\dfrac{(10m^5n^4)(5m^3n^6)}{25m^7n^5}\)

    6. \(\dfrac{(−18p^4q^7)(−6p^3q^8)}{−36p^{12}q^{10}}\)

    Réponse

    \(\dfrac{−3q^5}{p^5}\)

    7. \(\dfrac{(6a^4b^3)(4ab^5)}{(12a^2b)(a^3b)}\)

    8. \(\dfrac{(4u^2v^5)(15u^3v)}{(12u^3v)(u^4v)}\)

    Réponse

    \(\dfrac{5v^4}{u^2}\)

    Diviser un polynôme par un monomial

    Dans les exercices suivants, divisez chaque polynôme par le monomial.

    9. \((9n^4+6n^3)÷3n\)

    10. \((8x^3+6x^2)÷2x\)

    Réponse

    \(4x^2+3x\)

    11. \((63m^4−42m^3)÷(−7m^2)\)

    12. \((48y^4−24y^3)÷(−8y^2)\)

    Réponse

    \(−6y^2+3y\)

    13. \(\dfrac{66x^3y^2−110x^2y^3−44x^4y^3}{11x^2y^2}\)

    14. \(\dfrac{72r^5s^2+132r^4s^3−96r^3s^5}{12r^2s^2}\)

    Réponse

    \(6r^3+11r^2s−8rs^3\)

    15. \(10x^2+5x−4−5x\)

    16. \(20y^2+12y−1−4y\)

    Réponse

    \(−5y−3+\dfrac{1}{4y}\)

    Diviser les polynômes en utilisant la division longue

    Dans les exercices suivants, divisez chaque polynôme par le binôme.

    17. \((y^2+7y+12)÷(y+3)\)

    18. \((a^2−2a−35)÷(a+5)\)

    Réponse

    \(a−7\)

    19. \((6m^2−19m−20)÷(m−4)\)

    20. \((4x^2−17x−15)÷(x−5)\)

    Réponse

    \(4x+3\)

    21. \((q^2+2q+20)÷(q+6)\)

    22. \((p^2+11p+16)÷(p+8)\)

    Réponse

    \(p+3−\dfrac{8}{p+8}\)

    23. \((3b^3+b^2+4)÷(b+1)\)

    24. \((2n^3−10n+28)÷(n+3)\)

    Réponse

    \(\dfrac{2n^2−6n+8+4}{n+3}\)

    25. \((z^3+1)÷(z+1)\)

    26. \((m^3+1000)÷(m+10)\)

    Réponse

    \(m^2−10m+100\)

    27. \((64x^3−27)÷(4x−3)\)

    28. \((125y^3−64)÷(5y−4)\)

    Réponse

    \(25y^2+20x+16\)

    Diviser des polynômes en utilisant la division synthétique

    Dans les exercices suivants, utilisez la division synthétique pour trouver le quotient et le reste.

    29. \(x^3−6x^2+5x+14\)est divisé par\(x+1\)

    30. \(x^3−3x^2−4x+12\)est divisé par\(x+2\)

    Réponse

    \(x^2−5x+6; \space 0\)

    31. \(2x^3−11x^2+11x+12\)est divisé par\(x−3\)

    32. \(2x^3−11x^2+16x−12\)est divisé par\(x−4\)

    Réponse

    \(2x^2−3x+4; \space 4\)

    33. \(x^4-5x^2+2+13x+3\)est divisé par\(x+3\)

    34. \(x^4+x^2+6x−10\)est divisé par\(x+2\)

    Réponse

    \(x^3−2x^2+5x−4; \space −2\)

    35. \(2x^4−9x^3+5x^2−3x−6\)est divisé par\(x−4\)

    36. \(3x^4−11x^3+2x^2+10x+6\)est divisé par\(x−3\)

    Réponse

    \(3x^3−2x^2−4x−2;\space 0\)

    Diviser les fonctions polynomiales

    Dans les exercices suivants, divisez.

    37. Pour les fonctions\(f(x)=x^2−13x+36\) et\(g(x)=x−4\), trouvez ⓐ\(\left(\dfrac{f}{g}\right)(x)\) ⓑ\(\left(\dfrac{f}{g}\right)(−1)\)

    38. Pour les fonctions\(f(x)=x^2−15x+54\) et\(g(x)=x−9\), trouvez ⓐ\(\left(\dfrac{f}{g}\right)(x)\) ⓑ\(\left(\dfrac{f}{g}\right)(−5)\)

    Réponse

    ⓐ\(\left(\dfrac{f}{g}\right)(x)=x−6\)
    ⓑ\(\left(\dfrac{f}{g}\right)(−5)=−11\)

    39. Pour les fonctions\(f(x)=x^3+x^2−7x+2\) et\(g(x)=x−2\), trouvez ⓐ\(\left(\dfrac{f}{g}\right)(x)\) ⓑ\(\left(\dfrac{f}{g}\right)(2)\)

    40. Pour les fonctions\(f(x)=x^3+2x^2−19x+12\) et\(g(x)=x−3\), trouvez ⓐ\(\left(\dfrac{f}{g}\right)(x)\) ⓑ\(\left(\dfrac{f}{g}\right)(0)\)

    Réponse

    ⓐ\(\left(\dfrac{f}{g}\right)(x)=x^2+5x−4\)
    ⓑ\(\left(\dfrac{f}{g}\right)(0)=−4\)

    41. Pour les fonctions\(f(x)=x^2−5x+2\) et\(g(x)=x^2−3x−1\), trouvez ⓐ\((f·g)(x)\) ⓑ\((f·g)(−1)\)

    42. Pour les fonctions\(f(x)=x^2+4x−3\) et\(g(x)=x^2+2x+4\), trouvez ⓐ\((f·g)(x)\) ⓑ\((f·g)(1)\)

    Réponse

    ⓐ\((f·g)(x)=x^4+6x^3+9x^2+10x−12\) ; ⓑ\((f·g)(1)=14\)

    Utiliser le reste et le théorème des facteurs

    Dans les exercices suivants, utilisez le théorème du reste pour trouver le reste.

    43. \(f(x)=x^3−8x+7\)est divisé par\(x+3\)

    44. \(f(x)=x^3−4x−9\)est divisé par\(x+2\)

    Réponse

    \(−9\)

    45. \(f(x)=2x^3−6x−24\)divisé par\(x−3\)

    46. \(f(x)=7x^2−5x−8\)divisé par\(x−1\)

    Réponse

    \(−6\)

    Dans les exercices suivants, utilisez le théorème des facteurs pour déterminer si x−cx−c est un facteur de la fonction polynomiale.

    47. Déterminez si\(x+3\) un facteur de\(x^3+8x^2+21x+18\)

    48. Déterminez si\(x+4\) un facteur de\(x^3+x^2−14x+8\)

    Réponse

    non

    49. Déterminez si\(x−2\) un facteur de\(x^3−7x^2+7x−6\)

    50. Déterminez si\(x−3\) un facteur de\(x^3−7x^2+11x+3\)

    Réponse

    oui

    Exercices d'écriture

    51. James divise\(48y+6\) de\(6\) cette façon :\(\dfrac{48y+6}{6}=48y\). Qu'est-ce qui ne va pas dans son raisonnement ?

    52. Divisez\(\dfrac{10x^2+x−12}{2x}\) et expliquez avec des mots comment vous obtenez chaque terme du quotient.

    Réponse

    La réponse variera

    53. Expliquez quand vous pouvez utiliser la division synthétique.

    54. Dans vos propres mots, écrivez les étapes de la division synthétique pour\(x^2+5x+6\) diviser par\(x−2\).

    Réponse

    Les réponses peuvent varier.

    Auto-vérification

    a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section

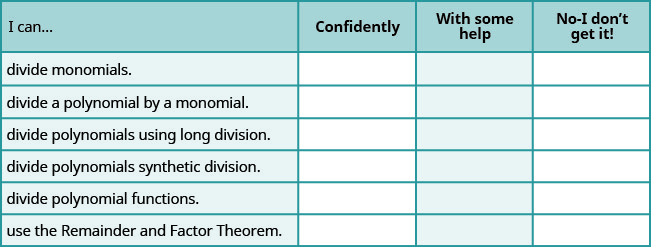
    La figure montre un tableau composé de sept lignes et de quatre colonnes. La première ligne est une ligne d'en-tête et elle étiquette chaque colonne. L'en-tête de la première colonne est « Je peux... », le second est « En toute confiance », le troisième est « avec de l'aide », « non moins, je ne comprends pas ! ». Sous la première colonne se trouvent les phrases « diviser les monômes », « diviser un polynôme en utilisant un monôme », « diviser les polynômes par division longue », « diviser les polynômes par division synthétique », « diviser les fonctions polynomiales » et « utiliser le théorème du reste et des facteurs ». Sous les deuxième, troisième et quatrième colonnes se trouvent des espaces vides où l'apprenant peut vérifier le niveau de maîtrise qu'il a atteint.

    b. Sur une échelle de 1 à 10, comment évalueriez-vous votre maîtrise de cette section à la lumière de vos réponses à la liste de contrôle ? Comment pouvez-vous améliorer cela ?