5.5 : Diviser des polynômes
- Page ID
- 194199
À la fin de cette section, vous serez en mesure de :
- Diviser les monômes
- Diviser un polynôme par un monomial
- Division de polynômes par division longue
- Division de polynômes par division synthétique
- Division des fonctions polynomiales
- Utilisez le reste et les théorèmes factoriels
Avant de commencer, répondez à ce questionnaire de préparation.
Diviser les monômes
Nous connaissons maintenant toutes les propriétés des exposants et les avons utilisées pour multiplier des polynômes. Nous utiliserons ensuite ces propriétés pour diviser les monômes et les polynômes.
Trouvez le quotient :\(54a^2b^3÷ (−6ab^5)\).
Solution
Lorsque nous divisons des monômes avec plus d'une variable, nous écrivons une fraction pour chaque variable.
\(\begin{array} {ll} {} &{54a^2b^3÷(−6ab^5)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{54a^2b^3}{−6ab^5}} \\[5pt] {\text{Use fraction multiplication.}} &{\dfrac{54}{−6}·\dfrac{a^2}{a}·\dfrac{b^3}{b^5}} \\[5pt] {\text{Simplify and use the Quotient Property.}} &{−9·a·\dfrac{1}{b^2}} \\[5pt] {\text{Multiply.}} &{−\dfrac{9a}{b^2}} \end{array}\)
Trouvez le quotient :\(−72a^7b^3÷(8a^{12}b^4)\).
- Réponse
-
\(−\dfrac{9}{a^5b}\)
Trouvez le quotient :\(−63c^8d^3÷(7c^{12}d^2)\).
- Réponse
-
\(\dfrac{−9d}{c^4}\)
Une fois que vous vous êtes familiarisé avec le processus et que vous l'avez pratiqué étape par étape à plusieurs reprises, vous pourrez peut-être en simplifier une fraction en une seule étape.
Trouvez le quotient :\(\dfrac{14x^7y^{12}}{21x^{11}y^6}\).
Solution
Veillez à simplifier\(\dfrac{14}{21}\) en divisant un facteur commun et à simplifier les variables en soustrayant leurs exposants.
\(\begin{array} {ll} {} &{\dfrac{14x^7y^{12}}{21x^{11}y^6}} \\ {\text{Simplify and use the Quotient Property.}} &{\dfrac{2y^6}{3x^4}} \\ \end{array}\)
Trouvez le quotient :\(\dfrac{28x^5y^{14}}{49x^9y^{12}}\).
- Réponse
-
\(\dfrac{4y^2}{7x^4}\)
Trouvez le quotient :\(\dfrac{30m^5n^{11}}{48m^{10}n^{14}}\).
- Réponse
-
\(\dfrac{5}{8m^5n^3}\)
Diviser un polynôme par un monomial
Maintenant que nous savons comment diviser un monôme par un monomial, la procédure suivante consiste à diviser un polynôme de deux termes ou plus par un monomial. La méthode que nous utiliserons pour diviser un polynôme par un monomial est basée sur les propriétés de l'addition de fractions. Nous allons donc commencer par un exemple pour examiner l'ajout de fractions. La somme se\(\dfrac{y}{5}+\dfrac{2}{5}\) simplifie en\(\dfrac{y+2}{5}\). Nous allons maintenant procéder à l'inverse pour diviser une seule fraction en fractions distinctes. Par exemple,\(\dfrac{y+2}{5}\) peut être écrit\(\dfrac{y}{5}+\dfrac{2}{5}\).
C'est « l'inverse » de l'addition de fractions et cela indique que si a, b et c sont des nombres où\(c\neq 0\), alors\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\). Nous l'utiliserons pour diviser les polynômes par les monômes.
Pour diviser un polynôme par un monomial, divisez chaque terme du polynôme par le monomial.
Trouvez le quotient :\((18x^3y−36xy^2)÷(−3xy)\).
Solution
\(\begin{array} {ll} {} &{(18x^3y−36xy^2)÷(−3xy)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{18x^3y−36xy^2}{−3xy}} \\[5pt] {\text{Divide each term by the divisor. Be careful with the signs!}} &{\dfrac{18x^3y}{−3xy}−\dfrac{36xy^2}{−3xy}} \\[5pt] {\text{Simplify.}} &{−6x^2+12y} \end{array}\)
Trouvez le quotient :\((32a^2b−16ab^2)÷(−8ab)\).
- Réponse
-
\(−4a+2b\)
Trouvez le quotient :\((−48a^8b^4−36a^6b^5)÷(−6a^3b^3)\).
- Réponse
-
\(8a^5b+6a^3b^2\)
Diviser les polynômes en utilisant la division longue
Divisez un polynôme par un binôme, nous suivons une procédure très similaire à la division longue des nombres. Examinons donc attentivement les étapes à suivre lorsque nous divisons un nombre à 3 chiffres, 875, par un nombre à 2 chiffres, 25.
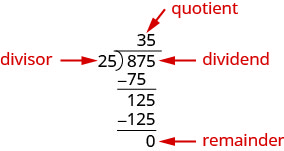
On vérifie la division en multipliant le quotient par le diviseur. Si nous avons fait la division correctement, le produit devrait être égal au dividende.
\[\begin{array} {l} {35·25} \\ {875\checkmark} \\ \nonumber \end{array}\]
Nous allons maintenant diviser un trinôme par un binôme. Au fur et à mesure que vous lisez l'exemple, remarquez à quel point les étapes sont similaires à celles de l'exemple numérique ci-dessus.
Trouvez le quotient :\((x^2+9x+20)÷(x+5)\).
Solution
| \(\require{enclose}\) | \(\qquad (x^2+9x+20) \div (x+5)\) |
| Écrivez-le comme un problème de division longue. Assurez-vous que le dividende est sous forme standard. |
\(\qquad x+5\enclose{longdiv}{ x^2+9x+20\phantom{0}} \) |
|
Divisez\(x^2\) par\(x\). Il peut être utile de se demander : «\(x\) Par quoi dois-je multiplier |
\(\qquad \begin{array}{r} {\color{red}x}\hspace{2.3em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{ {\color{red}x^2}+9x+20\phantom{0}} \end{array}\) |
| Mettez la réponse,\(x\), dans le quotient sur le\(x\) terme. \(x\)Multipliez par\(x+5\). Alignez les conditions similaires sous le dividende. |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+9x+20\phantom{0}}\\[-3pt] \underline{\color{red}x^2+5x}\hspace{2.4em} \end{array}\) |
| Soustraire\(x^2+5x\) de\(x^2+9x\). Il vous sera peut-être plus facile de modifier les signes, puis de les ajouter. Ensuite, annulez le dernier mandat,\(20.\) |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x+20}\hspace{0.5em} \end{array}\) |
Divisez\(4x\) par\(x\). Il peut être utile de se demander : «\(x\) Par quoi dois-je multiplier pour obtenir\(4x\) ? » Mettez la réponse,\(4\), dans le quotient sur le terme constant. |
\(\qquad \begin{array}{r}x+\phantom{0}{\color{red}4}\hspace{.5em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x}+20\hspace{0.5em} \end{array}\) |
| Multipliez 4 fois\(x+5\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{0.5em}\\[-3pt] \underline{ \color{red}4x+20}\hspace{.5em} \end{array}\) |
| Soustraire\(4x+20\) de\(4x+20\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{.5em}\\[-3pt] \underline{{\color{red}-}4x+({\color{red}-}20)}\\[-3pt] 0\hspace{.33em}\end{array}\) |
|
Vérifiez : \(\begin{array} {ll} {\text{Multiply the quotient by the divisor.}} &{(x+4)(x+5)} \\ {\text{You should get the dividend.}} &{x^2+9x+20\checkmark}\\ \end{array}\) |
Trouvez le quotient :\((y^2+10y+21)÷(y+3)\).
- Réponse
-
\(y+7\)
Trouvez le quotient :\((m^2+9m+20)÷(m+4)\).
- Réponse
-
\(m+5\)
Lorsque nous avons divisé 875 par 25, nous n'avions plus de reste. Mais parfois, la division des nombres laisse du reste. Il en va de même lorsque nous divisons des polynômes. Dans l'exemple suivant, nous aurons une division qui laissera un reste. Nous écrivons le reste sous forme de fraction avec le diviseur comme dénominateur.
Revenez sur les dividendes présentés dans les exemples précédents. Les termes étaient écrits par ordre décroissant de degrés et aucun diplôme ne manquait. Dans cet exemple, le dividende sera de\(x^4−x^2+5x−6\). Il manque un\(x^3\) terme. Nous l'ajouterons\(0x^3\) comme espace réservé.
Trouvez le quotient :\((x^4−x^2+5x−6)÷(x+2)\).
Solution
Notez qu'il n'y a pas de\(x^3\) terme dans le dividende. Nous l'ajouterons\(0x^3\) comme espace réservé.
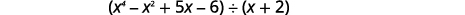 |
|
| Écrivez-le comme un problème de division longue. Assurez-vous que le dividende est sous une forme standard avec des espaces réservés pour les termes manquants. | 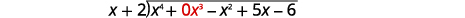 |
| Divisez\(x^4\) par\(x\). Mettez la réponse,\(x^3\), dans le quotient sur le\(x^3\) terme. \(x^3\)Multipliez par\(x+2\). Alignez les termes similaires. Soustrayez puis réduisez le terme suivant. |
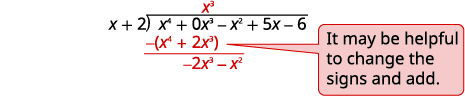 |
| Divisez\(−2x^3\) par\(x\). Mettez la réponse,\(−2x^2\), dans le quotient sur le\(x^2\) terme. \(−2x^2\)Multipliez par\(x+1\). Alignez les termes similaires Soustraire et réduisez le terme suivant. |
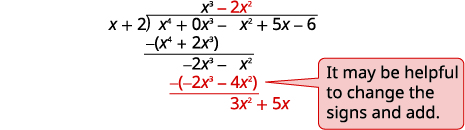 |
| Divisez\(3x^2\) par\(x\). Mettez la réponse,\(3x\), dans le quotient sur le\(x\) terme. \(3x\)Multipliez par\(x+1\). Alignez les termes similaires. Soustrayez et réduisez le terme suivant. |
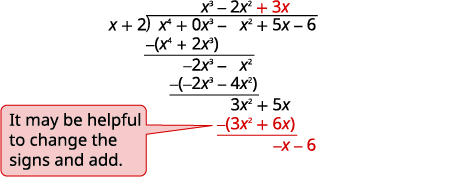 |
| Divisez\(−x\) par\(x\). Mettez la réponse,\(−1\), dans le quotient sur le terme constant. \(−1\)Multipliez par\(x+1\). Alignez les termes similaires. Changez les signes, ajoutez. Écrivez le reste sous forme de fraction avec le diviseur comme dénominateur. |
 |
| Pour vérifier, multipliez\((x+2)(x^3−2x^2+3x−1−4x+2)\). Le résultat devrait être\(x^4−x^2+5x−6\). |
Trouvez le quotient :\((x^4−7x^2+7x+6)÷(x+3)\).
- Réponse
-
\(x^3−3x^2+2x+1+3x+3\)
Trouvez le quotient :\((x^4−11x^2−7x−6)÷(x+3)\).
- Réponse
-
\(x^3−3x^2−2x−1−3x+3\)
Dans l'exemple suivant, nous allons diviser par\(2a−3\). Lorsque nous divisons, nous devrons prendre en compte les constantes ainsi que les variables.
Trouvez le quotient :\((8a^3+27)÷(2a+3)\).
Solution
Cette fois, nous allons montrer la division en une seule étape. Nous devons ajouter deux espaces réservés pour diviser.
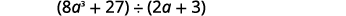 |
|
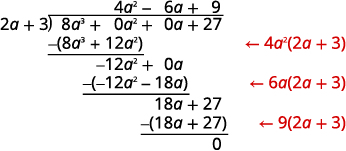 |
Pour vérifier, multipliez\((2a+3)(4a^2−6a+9)\).
Le résultat devrait être\(8a^3+27\).
Trouvez le quotient :\((x^3−64)÷(x−4)\).
- Réponse
-
\(x^2+4x+16\)
Trouvez le quotient :\((125x^3−8)÷(5x−2)\).
- Réponse
-
\(25x^2+10x+4\)
Diviser des polynômes en utilisant la division synthétique
Comme nous l'avons déjà mentionné, les mathématiciens aiment trouver des modèles pour faciliter leur travail. Comme la division longue peut être fastidieuse, revenons sur la division longue que nous avons faite dans Example et cherchons quelques modèles. Nous l'utiliserons comme base pour ce que l'on appelle la division synthétique. Le même problème dans le format de division synthétique est illustré ci-dessous.
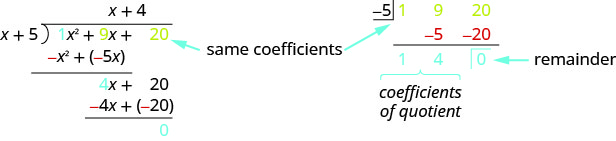
La division synthétique supprime simplement les variables et les nombres répétés inutiles. Ici, tous les\(x\) et\(x^2\) sont supprimés. ainsi que les\(−x^2\) et\(−4x\) car ils sont opposés au terme ci-dessus.
- La première ligne de la division synthétique correspond aux coefficients du dividende. Le\(−5\) est l'opposé du 5 dans le diviseur.
- La deuxième ligne de la division synthétique contient les nombres indiqués en rouge dans le problème de division.
- La troisième ligne de la division synthétique contient les chiffres indiqués en bleu dans le problème de division.
Notez que le quotient et le reste sont indiqués dans la troisième rangée.
\[\text{Synthetic division only works when the divisor is of the form }x−c. \nonumber \]
L'exemple suivant explique le processus.
Utilisez la division synthétique pour déterminer le quotient et le reste lorsqu'il\(2x^3+3x^2+x+8\) est divisé par\(x+2\).
Solution
| Écrivez le dividende avec une puissance décroissante de\(x\). | 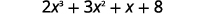 |
| Écrivez les coefficients des termes sur la première ligne de la division synthétique. |
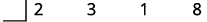 |
| Écrivez le diviseur as\(x−c\) et placez c dans la division synthétique de la case du diviseur. |
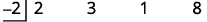 |
| Réduisez le premier coefficient à la troisième ligne. | 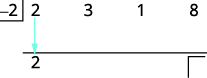 |
| Multipliez ce coefficient par le diviseur et placez le résultat sur la deuxième ligne sous le deuxième coefficient. |
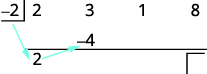 |
| Ajoutez la deuxième colonne, en plaçant le résultat sur la troisième ligne. | 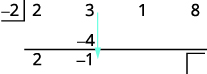 |
| Multipliez ce résultat par le diviseur et placez le résultat sur la deuxième ligne sous le troisième coefficient. |
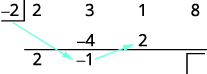 |
| Ajoutez la troisième colonne, en plaçant le résultat sur la troisième ligne. | 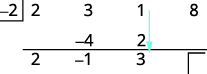 |
| Multipliez ce résultat par le diviseur et placez le résultat sur la troisième ligne sous le troisième coefficient. |
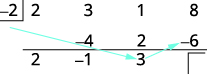 |
| Ajoutez la dernière colonne, en plaçant le résultat sur la troisième ligne. | 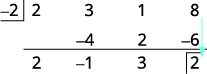 |
| Le quotient est de 2\(2x^2−1x+3\) et le reste est de 2. |
La division est terminée. Les chiffres de la troisième rangée nous donnent le résultat. Ce\(2\space\space\space−1\space\space\space3\) sont les coefficients du quotient. Le quotient est\(2x^2−1x+3\). Le 2 dans la case de la troisième rangée correspond au reste.
Vérifiez :
\(\begin{align} (\text{quotient})(\text{divisor}) + \text{remainder} &= \text{dividend} \nonumber\\ (2x^2−1x+3)(x+2)+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3−x^2+3x+4x^2−2x+6+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3+3x^2+x+8 &= 2x^3+3x^2+x+8\checkmark \nonumber \end{align} \)
Utilisez la division synthétique pour déterminer le quotient et le reste lorsqu'il\(3x^3+10x^2+6x−2\) est divisé par\(x+2\).
- Réponse
-
\(3x^2+4x−2;\space 2\)
Utilisez la division synthétique pour déterminer le quotient et le reste lorsqu'il\(4x^3+5x^2−5x+3\) est divisé par\(x+2\).
- Réponse
-
\(4x^2−3x+1; 1\)
Dans l'exemple suivant, nous allons effectuer toutes les étapes ensemble.
Utilisez la division synthétique pour déterminer le quotient et le reste lorsqu'il\(x^4−16x^2+3x+12\) est divisé par\(x+4\).
Solution
Le polynôme\(x^4−16x^2+3x+12\) a son terme dans l'ordre décroissant mais nous remarquons qu'il n'y a pas de\(x^3\) terme. Nous ajouterons un 0 comme espace réservé pour le\(x^3\) terme. Dans la\(x−c\) forme, le diviseur est\(x−(−4)\).
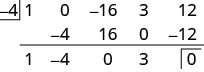
Nous avons divisé un\(4^{\text{th}}\) polynôme de\(1^{\text{st}}\) degrés par un polynôme de degrés, de sorte que le quotient sera un polynôme de\(3^{\text{rd}}\) degrés.
En lisant la troisième ligne, le quotient contient les coefficients\(1\space\space\space−4\space\space\space0\space\space\space3\), qui sont\(x^3−4x^2+3\). Le reste
est égal à 0.
Utilisez la division synthétique pour déterminer le quotient et le reste lorsqu'il\(x^4−16x^2+5x+20\) est divisé par\(x+4\).
- Réponse
-
\(x^3−4x^2+5;\space 0\)
Utilisez la division synthétique pour déterminer le quotient et le reste lorsqu'il\(x^4−9x^2+2x+6\) est divisé par\(x+3\).
- Réponse
-
\(x^3−3x^2+2;\space 0\)
Diviser les fonctions polynomiales
Tout comme les polynômes peuvent être divisés, les fonctions polynomiales peuvent également être divisées.
Pour les fonctions\(f(x)\) et\(g(x)\), où\(g(x)\neq 0\),
\[\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)} \nonumber\]
Pour les fonctions\(f(x)=x^2−5x−14\) et\(g(x)=x+2\), trouvez :
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−4)\).
Solution
ⓐ
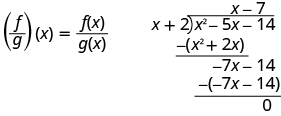
\(\begin{array} {ll} {\text{Substitute for }f(x)\text{ and }g(x).} &{\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2−5x−14}{x+2}} \\[5pt] {\text{Divide the polynomials.}} &{\left(\dfrac{f}{g}\right)(x)=x−7} \end{array} \)
ⓑ En partie ⓐ nous avons trouvé\(\left(\dfrac{f}{g}\right)(x)\) et on nous demande maintenant de le trouver\(\left(\dfrac{f}{g}\right)(−4)\).
\(\begin{array} {ll} {} &{\left(\dfrac{f}{g}\right)(x)=x−7} \\[5pt] {\text{To find }\left(\dfrac{f}{g}\right)(−4), \text{ substitute }x=−4.} &{\left(\dfrac{f}{g}\right)(−4)=−4−7} \\[5pt] {} &{\left(\dfrac{f}{g}\right)(−4)=−11} \end{array}\)
Pour les fonctions\(f(x)=x^2−5x−24\) et\(g(x)=x+3\), trouvez :
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−3)\).
- Répondez à une
-
\(\left(\dfrac{f}{g}\right)(x)=x−8\)
- Réponse b
-
\(\left(\dfrac{f}{g}\right)(−3)=−11\)
Pour les fonctions\(f(x)=x2−5x−36\) et\(g(x)=x+4\), trouvez :
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−5)\).
- Répondez à une
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
- Réponse b
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
Utiliser le reste et le théorème des facteurs
Regardons les problèmes de division que nous venons de résoudre et qui ont fini par être résolus. Ils sont résumés dans le tableau ci-dessous. Si nous prenons le dividende de chaque problème de division et que nous l'utilisons pour définir une fonction, nous obtenons les fonctions affichées dans le graphique. Lorsque le diviseur est écrit sous la forme\(x−c\), la valeur de la fonction at\(c\)\(f(c)\), est identique au reste du problème de division.
| dividende | Diviseur\(x−c\) | Reste | Fonction | \(f(c)\) |
|---|---|---|---|---|
| \(x^4−x^2+5x−6\) | \ (x−c \) » validation des données = « top">\(x−(−2)\) | \(−4\) | \(f(x)=x^4−x^2+5x−6\) | \ (f (c) \) » validation des données = « top">\(−4\) |
| \(3x^3−2x^2−10x+8\) | \ (x−c \) » validation des données = « top">\(x−2\) | 4 | \(f(x)=3x^3−2x^2−10x+8\) | \ (f (c) \) » validation des données = « top">4 |
| \(x^4−16x^2+3x+15\) | \ (x−c \) » validation des données = « top">\(x−(−4)\) | 3 | \(f(x)=x^4−16x^2+3x+15\) | \ (f (c) \) » validation des données = « top">3 |
Pour voir cela de manière plus générale, nous réalisons que nous pouvons corriger un problème de division en multipliant le quotient par le diviseur et en ajoutant le reste. En notation fonctionnelle, nous pourrions dire que pour obtenir le dividende\(f(x)\), nous multiplions le quotient,\(q(x)\) multiplions le diviseur et ajoutons le reste\(r\).\(x−c\)
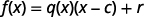 |
|
| Si nous évaluons cela à\(c\), nous obtenons : | 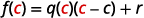 |
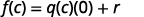 |
|
 |
Cela nous amène au théorème du reste.
Si la fonction polynomiale\(f(x)\) est divisée par\(x−c\), le reste l'est\(f(c)\).
Utilisez le théorème du reste pour trouver le reste lorsqu'il\(f(x)=x^3+3x+19\) est divisé par\(x+2\).
Solution
Pour utiliser le théorème du reste, nous devons utiliser le diviseur du\(x−c\) formulaire. Nous pouvons écrire le diviseur\(x+2\) comme\(x−(−2)\). Donc, le nôtre\(c\) est\(−2\).
Pour trouver le reste, nous évaluons\(f(c)\) lequel est\(f(−2)\).
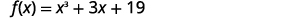 |
|
| Pour évaluer\(f(−2)\), remplacez\(x=−2\). | 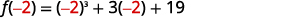 |
| Simplifiez. | 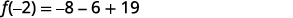 |
 |
|
| Le reste est égal à 5 lorsqu'\(f(x)=x^3+3x+19\)il est divisé par\(x+2\). | |
| Contrôle : utilisez une division synthétique pour vérifier. |
|
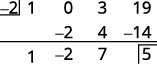 |
|
| Le reste est de 5. |
Utilisez le théorème du reste pour trouver le reste lorsqu'il\(f(x)=x^3+4x+15\) est divisé par\(x+2\).
- Réponse
-
\(−1\)
Utilisez le théorème du reste pour trouver le reste lorsqu'il\(f(x)=x^3−7x+12\) est divisé par\(x+3\).
- Réponse
-
\(6\)
Lorsque nous avons divisé\(8a^3+27\) par\(2a+3\) dans Exemple, le résultat était\(4a^2−6a+9\). Pour vérifier notre travail, nous multiplions\(4a2−6a+9\) par\(2a+3\) pour obtenir\(8a^3+27\).
\[(4a^2−6a+9)(2a+3)=8a^3+27 \nonumber \]
Ecrit de cette façon, nous pouvons le voir\(4a^2−6a+9\) et\(2a+3\) sommes des facteurs de\(8a^3+27\). Lorsque nous avons fait la division, le reste était nul.
Chaque fois qu'un diviseur\(x−c\),, divise une fonction polynomiale et donne un reste de zéro, nous disons que c'\(x−c\)est un facteur de\(f(x)\).\(f(x)\)
L'inverse est également vrai. Si\(x−c\) est un facteur de\(f(x)\) alors\(x−c\) divisera la fonction polynomiale, ce qui donne un reste de zéro.
Nous l'indiquerons dans le théorème des facteurs.
Pour toute fonction polynomiale\(f(x)\),
- si\(x−c\) est un facteur de\(f(x)\), alors\(f(c)=0\)
- si\(f(c)=0\), alors\(x−c\) est un facteur de\(f(x)\)
Utilisez le théorème du reste pour déterminer s'il\(x−4\) est un facteur de\(f(x)=x^3−64\).
Solution
Le théorème des facteurs nous indique que\(x−4\) c'est un facteur de\(f(x)=x^3−64\) si\(f(4)=0\).
\(\begin{array} {ll} {} &{f(x)=x^3−64} \\[5pt] {\text{To evaluate }f(4) \text{ substitute } x=4.} &{f(4)=4^3−64} \\[5pt] {\text{Simplify.}} &{f(4)=64−64} \\[5pt]{\text{Subtract.}} &{f(4)=0} \end{array}\)
Puisque\(f(4)=0, x−4\) est un facteur de\(f(x)=x^3−64\).
Utilisez le théorème des facteurs pour déterminer s'il s'\(x−5\)agit d'un facteur de\(f(x)=x^3−125\).
- Réponse
-
oui
Utilisez le théorème des facteurs pour déterminer s'il s'\(x−6\)agit d'un facteur de\(f(x)=x^3−216\).
- Réponse
-
oui
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à diviser des polynômes.
- Diviser un polynôme par un binôme
- Théorème synthétique de la division et du reste
Concepts clés
- Division d'un polynôme par un monomial
- Pour diviser un polynôme par un monomial, divisez chaque terme du polynôme par le monomial.
- Division des fonctions polynomiales
- Pour les fonctions\(f(x)\) et\(g(x)\), où\(g(x)\neq 0\),
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}\)
- Pour les fonctions\(f(x)\) et\(g(x)\), où\(g(x)\neq 0\),
- Théorème du reste
- Si la fonction polynomiale\(f(x)\) est divisée par\(x−c\), le reste l'est\(f(c)\).
- Théorème des facteurs : Pour toute fonction polynomiale\(f(x)\),
- si\(x−c\) est un facteur de\(f(x)\), alors\(f(c)=0\)
- si\(f(c)=0\), alors\(x−c\) est un facteur de\(f(x)\)


