5.4 : Multiplier les polynômes
- Page ID
- 194184
À la fin de cette section, vous serez en mesure de :
- Multiplier les monômes
- Multipliez un polynôme par un monomial
- Multipliez un binôme par un binôme
- Multiplier un polynôme par un polynôme
- Multiplier les produits spéciaux
- Multiplier les fonctions polynomiales
Avant de commencer, répondez à ce questionnaire de préparation.
Multiplier les monômes
Nous sommes prêts à effectuer des opérations sur des polynômes. Les monômes étant des expressions algébriques, nous pouvons utiliser les propriétés des exposants pour multiplier les monômes.
Multipliez :
- \((3x^2)(−4x^3)\)
- \(\left(\frac{5}{6}x^3y\right)(12xy^2).\)
- Répondez à une
-
\(\begin{array} {ll} {} &{(3x^2)(−4x^3)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{3·(−4)·x^2·x^3} \\ {\text{}} &{−12x^5} \\ \end{array} \)
- Réponse b
-
\(\begin{array} {ll} {} &{\left(\frac{5}{6}x^3y\right)(12xy^2)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{\frac{5}{6}·12·x^3·x·y·y^2} \\ {\text{Multiply.}} &{10x^4y^3} \\ \end{array} \)
Multipliez :
- \((5y^7)(−7y^4)\)
- \((25a^4b^3)(15ab^3)\)
- Répondez à une
-
\(−35y^{11}\)
- Réponse b
-
\(375 a^5b^6\)
Multipliez :
- \((−6b^4)(−9b^5)\)
- \((23r^5s)(12r^6s^7).\)
- Répondez à une
-
\(54b^9\)
- Réponse b
-
\(276 r^{11}s^8\)
Multiplier un polynôme par un monomial
Multiplier un polynôme par un monôme consiste simplement à appliquer la propriété distributive.
Multipliez :
- \(−2y(4y^2+3y−5)\)
- \(3x^3y(x^2−8xy+y^2)\).
- Répondez à une
-
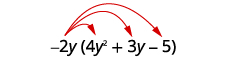
Distribuez. 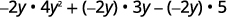
Multipliez. 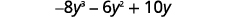
- Réponse b
-
\(\begin{array} {ll} {} &{3x^3y(x^2−8xy+y^2)} \\ {\text{Distribute.}} &{3x^3y⋅x^2+(3x^3y)⋅(−8xy)+(3x^3y)⋅y^2} \\ {\text{Multiply.}} &{3x^5y−24x^4y^2+3x^3y^3} \\ \end{array} \)
Multipliez :
- \(-3y(5y^2+8y^{7})\)
- \(4x^2y^2(3x^2−5xy+3y^2)\)
- Répondez à une
-
\(−15y^3−24y^8\)
- Réponse b
-
\(12x^4y^2−20x^3y^3+12x^2y^4\)
Multipliez :
- \(4x^2(2x^2−3x+5)\)
- \(−6a^3b(3a^2−2ab+6b^2)\)
- Répondez à une
-
\(8x^4−12x^3+20x^2\)
- Réponse b
-
\(−18a^5b+12a^4b^2−36a^3b^3\)
Multipliez un binôme par un binôme
Tout comme il existe différentes manières de représenter la multiplication de nombres, il existe plusieurs méthodes qui peuvent être utilisées pour multiplier un binôme par un binôme. Nous allons commencer par utiliser la propriété distributive.
Multipliez :
- \((y+5)(y+8)\)
- \((4y+3)(2y−5)\).
- Réponse
-
ⓐ
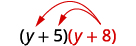
Distribuez\((y+8)\). 
Distribuez à nouveau. 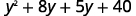
Combinez les mêmes termes. 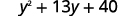
ⓑ
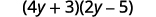
Distribuez. 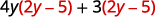
Distribuez à nouveau. 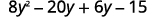
Combinez les mêmes termes. 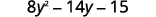
Multipliez :
- \((x+8)(x+9)\)
- \((3c+4)(5c−2)\).
- Répondez à une
-
\(x^2+17x+72\)
- Réponse b
-
\(15c^2+14c−8\)
Multipliez :
- \((5x+9)(4x+3)\)
- \((5y+2)(6y−3)\).
- Répondez à une
-
\(20x^2+51x+27\)
- Réponse b
-
\(30y^2−3y−6\)
Si vous multipliez les binômes assez souvent, vous remarquerez peut-être un schéma. Notez que le premier terme du résultat est le produit des premiers termes de chaque binôme. Les deuxième et troisième termes sont le produit de la multiplication des deux termes externes puis des deux termes internes. Et le dernier terme résulte de la multiplication des deux derniers termes,
Nous abrégeons « First, Outer, Inner, Last » en FOIL. Les lettres signifient « Premier, Extérieur, Intérieur, Dernier ». Nous utilisons cette méthode comme une autre méthode de multiplication des binômes. Le mot FOIL est facile à retenir et permet de trouver les quatre produits.
Multiplions\((x+3)(x+7)\) en utilisant les deux méthodes.

Nous résumons les étapes de la méthode FOIL ci-dessous. La méthode FOIL ne s'applique qu'à la multiplication de binômes, pas d'autres polynômes !

Lorsque vous multipliez par la méthode FOIL, tracer les lignes aidera votre cerveau à se concentrer sur le motif et à le rendre plus facile à appliquer.
Nous allons maintenant faire un exemple où nous utilisons le modèle FOIL pour multiplier deux binômes.
Multipliez :
- \((y−7)(y+4)\)
- \((4x+3)(2x−5)\).
- Réponse
-
un.

b.

Multipliez :
- \((x−7)(x+5)\)
- \((3x+7)(5x−2)\).
- Réponse
-
a.\(x^2−2x−35\)
b.\(15x^2+29x−14\)
Multipliez :
- \((b−3)(b+6)\)
- \((4y+5)(4y−10)\).
- Réponse
-
a.\(b^2+3b−18\)
b.\(16y^2−20y−50\)
Les produits finaux du dernier exemple étaient des trinômes, car nous pouvions combiner les deux termes intermédiaires. Ce n'est pas toujours le cas.
Multipliez :
- \((n^2+4)(n−1)\)
- \((3pq+5)(6pq−11)\).
- Réponse
-
un.
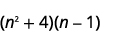
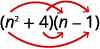
Étape 1 Multipliez les premiers termes. 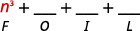
Étape 2 Multipliez les termes extérieurs. 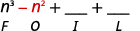
Étape 3. Multipliez les termes internes. 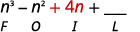
Étape 4. Multipliez les derniers termes. 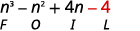
Étape 5. Combinez les mêmes termes, il n'y en a pas. 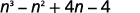
b.
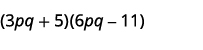
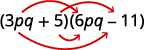
Étape 1 Multipliez les premiers termes. 
Étape 2 Multipliez les termes extérieurs. 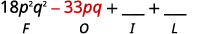
Étape 3. Multipliez les termes internes. 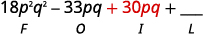
Étape 4. Multipliez les derniers termes. 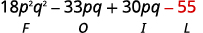
Étape 5. Combinez les mêmes termes. 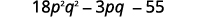
Multipliez :
- \((x^2+6)(x−8)\)
- \((2ab+5)(4ab−4)\).
- Réponse
-
a.\(x^3−8x^2+6x−48\)
b.\(8a^2b^2+12ab−20\)
Multipliez :
- \((y^2+7)(y−9)\)
- \((2xy+3)(4xy−5)\).
- Réponse
-
a.\(y^3−9y^2+7y−63\)
b.\(8x^2y^2+2xy−15\)
La méthode FOIL est généralement la méthode la plus rapide pour multiplier deux binômes, mais elle ne fonctionne que pour les binômes. Vous pouvez utiliser la propriété distributive pour trouver le produit de deux polynômes quelconques. Une autre méthode qui fonctionne pour tous les polynômes est la méthode verticale. Elle ressemble beaucoup à la méthode que vous utilisez pour multiplier des nombres entiers. Examinez attentivement cet exemple de multiplication de nombres à deux chiffres.

Nous allons maintenant appliquer cette même méthode pour multiplier deux binômes.
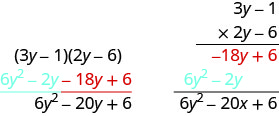
Multipliez en utilisant la méthode verticale :\((3y−1)(2y−6)\).
- Réponse
-
Peu importe le binôme qui se trouve en haut.
\ (\ begin {align*} & & & & & \ quad \ ; ; \ ; 3 ans - 1 \ \ [4 points]
& & & \ underline {\ quad \ times \ ; 2y-6} \ \ [4 points]
& \ text {Multipliez} 3y-1 \ text {par} -6. & & \ quad -18y + 6 & & \ text {produit partiel} \ \ [4 points]
& \ text {Multipliez} 3y-1 \ text {par} 2 ans. & & \ underline {6y^2 - 2 ans} & & \ text {produit partiel} \ \ [4 points]
& \ text {Ajoutez des termes similaires.} & & 6y^2 - 20 ans + 6 \ end {align*} \)Notez que les produits partiels sont identiques aux termes de la méthode FOIL.
Multipliez en utilisant la méthode verticale :\((5m−7)(3m−6)\).
- Réponse
-
\(15m^2−51m+42\)
Multipliez en utilisant la méthode verticale :\((6b−5)(7b−3)\).
- Réponse
-
\(42b^2−53b+15\)
Nous avons maintenant utilisé trois méthodes pour multiplier les binômes. Assurez-vous de pratiquer chaque méthode et essayez de décider laquelle vous préférez. Les méthodes sont répertoriées ici dans leur intégralité, pour vous aider à vous en souvenir.
Pour multiplier des binômes, utilisez :
- Propriété distributive
- Méthode FOIL
- Méthode verticale
Multiplier un polynôme par un polynôme
Nous avons multiplié les monômes par les monômes, les monômes par les polynômes et les binômes par les binômes. Nous sommes maintenant prêts à multiplier un polynôme par un polynôme. N'oubliez pas que FOIL ne fonctionnera pas dans ce cas, mais nous pouvons utiliser la propriété distributive ou la méthode verticale.
Multipliez\((b+3)(2b^2−5b+8)\) en utilisant ⓐ la propriété distributive et ⓑ la méthode verticale.
- Réponse
-
un.
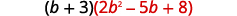
Distribuez. 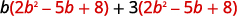
Multipliez. 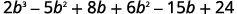
Combinez les mêmes termes. 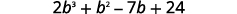
b. Il est plus facile de placer le polynôme avec moins de termes en bas, car nous obtenons ainsi moins de produits partiels.
Multipliez\((2b^2−5b+8)\) par 3.
Multipliez\((2b^2−5b+8)\) par\(b\).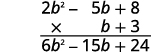
Ajoutez des termes similaires. 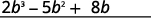
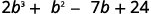
Multipliez\((y−3)(y^2−5y+2)\) en utilisant ⓐ la propriété distributive et ⓑ la méthode verticale.
- Réponse
-
a.\(y^3−8y^2+17y−6\)
b.\(y^3−8y^2+17y−6\)
Multipliez\((x+4)(2x^2−3x+5)\) en utilisant a) la propriété distributive et b) la méthode verticale.
- Réponse
-
a. et b.\(2x^3+5x^2−7x+20\)
Nous avons maintenant vu deux méthodes que vous pouvez utiliser pour multiplier un polynôme par un polynôme. Après avoir pratiqué chaque méthode, vous constaterez probablement que vous préférez une méthode à l'autre. Nous listons que les deux méthodes sont répertoriées ici, pour faciliter la consultation.
Pour multiplier un trinôme par un binôme, utilisez :
- Propriété distributive
- Méthode verticale
Multiplier les produits spéciaux
Les mathématiciens aiment rechercher des modèles qui faciliteront leur travail. La mise au carré des binômes en est un bon exemple. Bien que vous puissiez toujours obtenir le produit en écrivant le binôme deux fois et en les multipliant, il y a moins de travail à faire si vous apprenez à utiliser un modèle. Commençons par examiner trois exemples et cherchons un modèle.
Regardez ces résultats. Voyez-vous des modèles ?
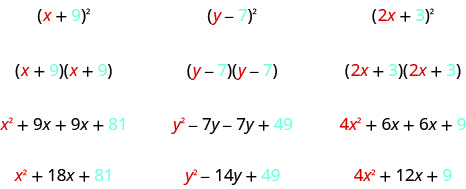
Qu'en est-il du nombre de termes ? Dans chaque exemple, nous avons quadrillé un binôme et le résultat a été un trinôme.
\[(a+b)^2=\text{___}+\text{___}+\text{___} \nonumber\]
Maintenant, regardez le premier terme de chaque résultat. D'où vient-il ?
Le premier terme est le produit des premiers termes de chaque binôme. Les binômes étant identiques, il ne s'agit que du carré du premier terme !
\[(a+b)^2=a^2+\text{___}+\text{___} \nonumber\]
Pour obtenir le premier terme du produit, mettez le premier terme au carré.
D'où vient le dernier mandat ? Regardez les exemples et trouvez le modèle.
Le dernier terme est le produit des derniers termes, qui est le carré du dernier terme.
\[(a+b)^2=\text{___}+\text{___}+b^2 \nonumber\]
Pour obtenir le dernier terme du produit, mettez le dernier terme au carré.
Enfin, regardez le moyen terme. Remarquez que cela vient de l'ajout des termes « extérieur » et « intérieur », qui sont tous deux identiques ! Le terme moyen est donc le double du produit des deux termes du binôme.
\[(a+b)^2=\text{___}+2ab+\text{___} \nonumber\]
\[(a−b)^2=\text{___}−2ab+\text{___} \nonumber\]
Pour obtenir le terme moyen du produit, multipliez les termes et doublez leur produit.
Réunir tout cela :
Si a et b sont des nombres réels,

Pour mettre un binôme au carré, quadriller le premier terme, mettre au carré le dernier terme, doubler leur produit.
Multipliez : a.\((x+5)^2\)\((2x−3y)^2\) b.
- Réponse
-
un.
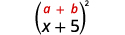
Qualifiez le premier mandat. 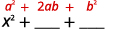
Qualifier le dernier mandat. 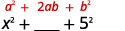
Doublez leur produit. 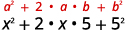
Simplifiez. 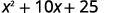
b.
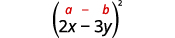
Utilise le motif. 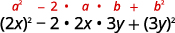
Simplifiez. 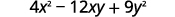
Multipliez : a.\((x+9)^2\)\((2c−d)^2\) b.
- Réponse
-
a.\(x^2+18x+81\)
b.\(4c^2−4cd+d^2\)
Multipliez : a.\((y+11)^2\)\((4x−5y)^2\) b.
- Réponse
-
a.\(y^2+22y+121\)
b.\(16x^2−40xy+25y^2\)
Nous venons de voir un modèle de quadrature des binômes que nous pouvons utiliser pour faciliter la multiplication de certains binômes. De même, il existe un modèle pour un autre produit de binômes. Mais avant d'y aller, nous devons introduire du vocabulaire.
Une paire de binômes qui ont chacun le même premier terme et le même dernier terme, mais l'un est une somme et l'autre est une différence est appelée paire conjuguée et est de la forme\((a−b)\),\((a+b)\).
Une paire conjuguée est constituée de deux binômes de la forme
\[(a−b), (a+b). \nonumber\]
Les deux binômes ont chacun le même premier terme et le même dernier terme, mais l'un des binômes est une somme et l'autre une différence.
Il existe un bon modèle pour trouver le produit des conjugués. Vous pouvez, bien sûr, simplement FOIL pour obtenir le produit, mais l'utilisation du patron facilite votre travail. Cherchons le modèle en utilisant FOIL pour multiplier certaines paires conjuguées.
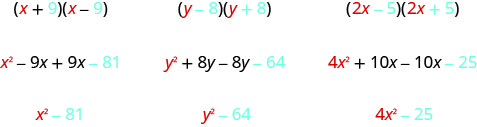
Qu'observez-vous à propos des produits ?
Le produit des deux binômes est également un binôme ! La plupart des produits issus du FOIL sont des trinômes.
Chaque premier terme est le produit des premiers termes des binômes, et comme ils sont identiques, il s'agit du carré du premier terme.
\[(a+b)(a−b)=a^2−\text{___} \nonumber\]
Pour obtenir le premier terme, mettez le premier terme au carré.
Le dernier terme est obtenu en multipliant les derniers termes, le carré du dernier terme.
\[(a+b)(a−b)=a^2−b^2 \nonumber\]
Pour obtenir le dernier terme, mettez le dernier terme au carré.
Pourquoi n'y a-t-il pas de moyen terme ? Remarquez que les deux termes intermédiaires que vous obtenez avec FOIL se combinent à 0 dans tous les cas, résultat d'une addition et d'une soustraction.
Le produit des conjugués est toujours de la forme\(a^2−b^2\). C'est ce qu'on appelle une différence de carrés.
Cela conduit au schéma suivant :
Si a et b sont des nombres réels,

Le produit s'appelle une différence de carrés.
Pour multiplier des conjugués, mettez le premier terme au carré, le dernier terme au carré, écrivez-le comme une différence de carrés.
Multipliez en utilisant le produit du schéma des conjugués : a.\((2x+5)(2x−5)\)\((5m−9n)(5m+9n)\) b.
- Réponse
-
un.
Les binômes sont-ils conjugués ? 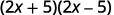
C'est le produit de conjugués. 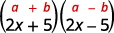
Mettre le premier terme au carré, 2xx2. 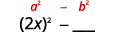
Mettre au carré le dernier terme, 5.5. 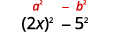
Simplifiez. Le produit est une différence de carrés. 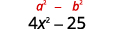
b.
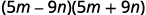
Cela correspond au modèle. 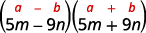
Utilise le motif. 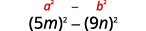
Simplifiez. 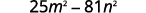
Multipliez : a.\((6x+5)(6x−5)\)\((4p−7q)(4p+7q)\) b.
- Réponse
-
a.\(36x^2−25\)
b.\(16p^2−49q^2\)
Multipliez : a.\((2x+7)(2x−7)\)\((3x−y)(3x+y)\) b.
- Réponse
-
a.\(4x^2−49\) b.\(9x^2−y^2\)
Nous venons de développer des modèles de produits spéciaux pour les carrés binomiaux et pour le produit des conjugués. Les produits se ressemblent, il est donc important de savoir quand il est approprié d'utiliser chacun de ces modèles et de remarquer en quoi ils diffèrent. Examinez les deux modèles ensemble et notez leurs similitudes et leurs différences.
| Carrés binomiaux | Produit de conjugués |
|---|---|
| \((a+b)^2=a^2+2ab+b^2\) | \((a−b)(a+b)=a^2−b^2\) |
| \((a−b)^2=a^2−2ab+b^2\) | |
| • Mise au carré d'un binôme | • Multiplier les conjugués |
| • Le produit est un trinôme | • Le produit est un binôme. |
| • Les termes intérieurs et extérieurs de FOIL sont les mêmes. | • Les termes intérieurs et extérieurs avec FOIL sont opposés. |
| • Le moyen terme est le double du produit des termes | • Il n'y a pas de moyen terme. |
Choisissez le motif approprié et utilisez-le pour trouver le produit :
a.\((2x−3)(2x+3)\) b.\((8x-5)^2\) c.\((6m+7)^2\)\((5x−6)(6x+5)\) d.
- Réponse
-
un.\((2x−3)(2x+3)\)
Ce sont des conjugués. Ils ont les mêmes premiers nombres et les mêmes derniers chiffres, et un binôme est une somme et l'autre une différence. Il correspond au modèle Product of Conjugués.
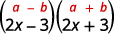
Utilise le motif. 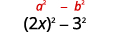
Simplifiez. 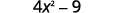
b.\((8x−5)^2\)
On nous demande de quadriller un binôme. Il correspond au motif des carrés binomiaux.
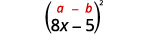
Utilise le motif. 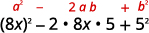
Simplifiez. 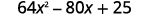
c.\((6m+7)^2\)
Encore une fois, nous allons mettre un binôme au carré, donc nous utilisons le modèle des carrés binomiaux.
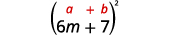
Utilise le motif. 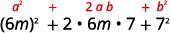
Simplifiez. 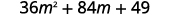
d.\((5x−6)(6x+5)\)
Ce produit ne correspond pas aux motifs, nous utiliserons donc du FOIL.
\(\begin{array} {ll} {} &{(5x−6)(6x+5)} \\ {\text{Use FOIL.}} & {30x^2+25x−36x−30} \\ {\text{Simplify.}} & {30x^2−11x−30} \\ \end{array}\)
Choisissez le motif approprié et utilisez-le pour trouver le produit :
a.\((9b−2)(2b+9)\) b.\((9p−4)^2\) c.\((7y+1)^2\)\((4r−3)(4r+3)\) d.
- Réponse
-
a. FOIL ;\(18b^2+77b−18\)
b. Carrés binomiaux ;\(81p^2−72p+16\)
c. Carrés binomiaux ;\(49y^2+14y+1\)
d. Produit de conjugués ;\(16r^2−9\)
Choisissez le motif approprié et utilisez-le pour trouver le produit :
a.\((6x+7)^2\) b.\((3x−4)(3x+4)\) c.\((2x−5)(5x−2)\)\((6n−1)^2\) d.
- Réponse
-
a. Carrés binomiaux ;\(36x^2+84x+49\) b. Produit des conjugués ;\(9x^2−16\) c. FOIL ;\(10x^2−29x+10\) d. Carrés binomiaux ;\(36n^2−12n+1\)
Multiplier les fonctions polynomiales
Tout comme les polynômes peuvent être multipliés, les fonctions polynomiales peuvent également être multipliées.
Pour les fonctions\(f(x)\) et\(g(x)\),
\[(f·g)(x)=f(x)·g(x)\]
Pour les fonctions\(f(x)=x+2\) et\(g(x)=x^2−3x−4\), trouvez :
- \((f·g)(x)\)
- \((f·g)(2)\).
- Réponse
-
un.
\(\begin{array} {ll} {} &{(f·g)(x)=f(x)·g(x)} \\ {\text{Substitute for } f(x) \text{ and } g(x)} &{(f·g)(x)=(x+2)(x^2−3x−4)} \\ {\text{Multiply the polynomials.}} &{(f·g)(x)=x(x^2−3x−4)+2(x^2−3x−4)} \\ {\text{Distribute.}} &{(f·g)(x)=x3−3x^2−4x+2x^2−6x−8} \\ {\text{Combine like terms.}} &{(f·g)(x)=x3−x^2−10x−8} \\ \end{array}\)
b. Dans la partie a. nous avons trouvé\((f·g)(x)\) et on nous demande maintenant de le trouver\((f·g)(2)\).
\(\begin{array} {ll} {} &{(f·g)(x)=x^3−x^2−10x−8} \\ {\text{To find }(f·g)(2), \text{ substitute } x=2.} &{(f·g)(2)=2^3−2^2−10·2−8} \\ {} &{(f·g)(2)=8−4−20−8} \\ {} &{(f·g)(2)=−24} \\ \end{array}\)
Pour les fonctions\(f(x)=x−5\) et\(g(x)=x^2−2x+3\), trouvez
- \((f·g)(x)\)
- \((f·g)(2)\).
- Répondez à une
-
\((f·g)(x)=x^3−7x^2+13x−15\)
- Réponse b
-
\((f·g)(2)=−9\)
Pour les fonctions\(f(x)=x−7\) et\(g(x)=x^2+8x+4\), trouvez
- \((f·g)(x)\)
- \((f·g)(2)\).
- Répondez à une
-
\((f·g)(x)=x^3+x^2−52x−28\)
- Répondez à une
-
\((f·g)(2)=−120\)
Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur la multiplication des polynômes.
- Introduction aux produits spéciaux des binômes
Concepts clés
- Comment utiliser la méthode FOIL pour multiplier deux binômes.
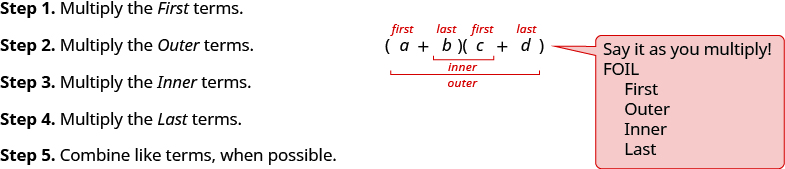
- Multiplier deux binômes : Pour multiplier des binômes, utilisez :
- Propriété distributive
- Méthode FOIL
- Multiplier un polynôme par un polynôme : Pour multiplier un trinôme par un binôme, utilisez :
- Propriété distributive
- Méthode verticale
- Modèle de carrés binomiaux
Si a et b sont des nombres réels,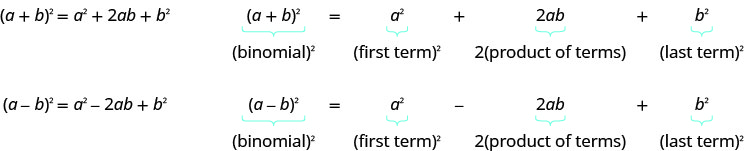
- Produit du modèle conjugué
Si a, b sont des nombres réels
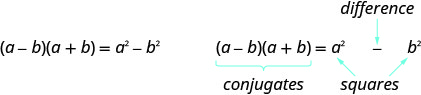
Le produit est appelé différence de carrés.
Pour multiplier des conjugués, mettez le premier terme au carré, le dernier terme au carré, écrivez-le comme une différence de carrés. - Comparaison des modèles de produits spéciaux
Carrés binomiaux Produit de conjugués \((a+b)^2=a^2+2ab+b^2\) \((a−b)^2=a^2−2ab+b^2\) \((a−b)(a+b)=a^2−b^2\) • Mise au carré d'un binôme • Multiplier les conjugués • Le produit est un trinôme • Le produit est un binôme. • Les termes intérieurs et extérieurs de FOIL sont les mêmes. • Les termes intérieurs et extérieurs avec FOIL sont opposés. • Le moyen terme est le double du produit des termes • Il n'y a pas de moyen terme. - Multiplication des fonctions polynomiales :
- Pour les fonctions\(f(x)\) et\(g(x)\),
\[(f⋅g)(x)=f(x)⋅g(x) \nonumber\]
- Pour les fonctions\(f(x)\) et\(g(x)\),
Lexique
- paire conjuguée
- Une paire conjuguée est constituée de deux binômes de la forme\((a−b)\) et\((a+b)\). Les deux binômes ont chacun le même premier terme et le même dernier terme, mais l'un des binômes est une somme et l'autre une différence.


