Skip to main content
Global

3.5 : Représenter graphiquement les inégalités linéaires dans deux variables

  1. Last updated
  2. Save as PDF
  • Page ID
    194104

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    RÉSUMÉ

    À la fin de cette section, vous serez en mesure de :

    • Vérifiez les solutions à une inégalité entre deux variables.
    • Reconnaissez la relation entre les solutions d'une inégalité et son graphe.
    • Représenter graphiquement les inégalités linéaires en deux variables
    • Résolvez des applications en utilisant des inégalités linéaires dans deux variables

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Graphe\(x>2\) sur une ligne numérique.
      Si vous avez oublié ce problème, consultez [lien].
    2. Résoudre :\(4x+3>23\).
      Si vous avez oublié ce problème, consultez [lien].
    3. Traduire :\(8<x>3\).
      Si vous avez oublié ce problème, consultez [lien].

    Vérifier les solutions à une inégalité entre deux variables

    Auparavant, nous avons appris à résoudre les inégalités avec une seule variable. Nous allons maintenant en apprendre davantage sur les inégalités contenant deux variables. Nous examinerons en particulier les inégalités linéaires entre deux variables qui sont très similaires aux équations linéaires entre deux variables.

    Les inégalités linéaires entre deux variables ont de nombreuses applications. Si vous dirigiez une entreprise, par exemple, vous souhaiteriez que vos revenus soient supérieurs à vos coûts, afin que votre entreprise réalise des bénéfices.

    INÉGALITÉ LINÉAIRE

    Une inégalité linéaire est une inégalité qui peut être écrite sous l'une des formes suivantes :

    \( \begin{array} {l} { }& {Ax+By>C} &{Ax+By\geq C} &{Ax+By<C} &{Ax+By\leq C} \\ \end{array} \)

    Où A et B ne sont pas tous deux nuls.

    Rappelons qu'une inégalité avec une seule variable avait de nombreuses solutions. Par exemple, la solution à l'inégalité x>3x>3 est un nombre supérieur à 3. Nous l'avons montré sur la ligne numérique en ombrant la ligne numérique à droite de 3 et en plaçant une parenthèse ouverte à 3. Voir la figure.

    Image de la ligne numérique avec les nombres entiers de moins 5 à 5. La partie de la ligne numérique située à droite du chiffre 3 est marquée par une ligne bleue. Le chiffre 3 est marqué par une parenthèse ouverte bleue.
    Figurine\(\PageIndex{1}\)

    De même, les inégalités linéaires entre deux variables ont de nombreuses solutions. Toute paire ordonnée (x, y) (x, y) qui crée une inégalité lorsque nous la substituons dans les valeurs est une solution à une inégalité linéaire.

    Solution à une inégalité linéaire

    Une paire ordonnée\((x,y)\) est une solution à une inégalité linéaire si l'inégalité est vraie lorsque nous substituons les valeurs de x et de y.

    Index de page {1} \)

    Déterminez si chaque paire ordonnée est une solution à l'inégalité y>x+4:y>x+4 :

    ⓐ (0,0) (0,0) ⓑ (1,6) (1,6) ⓒ (2,6) (2,6) ⓓ (−5, −15) (−5, −15) ⓔ (−8,12) (−8,12) (−8,12)

    Réponse

    ⓐ

    \((0,0)\) .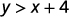
    . .
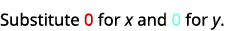
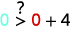
    Simplifiez. .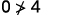
     

    Donc, n'\((0,0)\)est pas une solution à\(y>x+4\).

    ⓑ

    \((1,6)\) .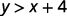
    . .
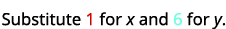
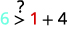
    Simplifiez. .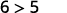
      Donc,\((1,6)\) est une solution pour\(y>x+4\).

    ⓒ

    \((2,6)\) .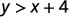
    . .
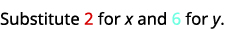
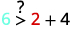
    Simplifiez. .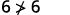
      Donc, n'\((2,6)\)est pas une solution à\(y>x+4\).

    ⓓ

    \((−5,−15)\) .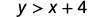
    . .
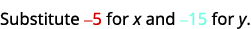
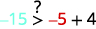
    Simplifiez. .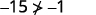
      Donc, n'\((−5,−15)\)est pas une solution à\(y>x+4\).

    ⓔ

    \((−8,12)\) .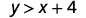
    . .
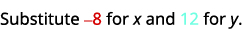
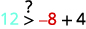
    Simplifiez. .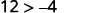
      Donc,\((−8,12)\) est une solution pour\(y>x+4\).

    Déterminez si chaque paire ordonnée est une solution à l'inégalité\(y>x−3\) :

    ⓐ\((0,0)\) ⓑ\((4,9)\) ⓒ\((−2,1)\) ⓓ\((−5,−3)\) ⓔ\((5,1)\)

    Réponse

    ⓐ oui ⓑ oui ⓒ oui ⓓ oui ⓔ non

    Exemple\(\PageIndex{3}\)

    Déterminez si chaque paire ordonnée est une solution à l'inégalité\(y<x+1\) :

    ⓐ\((0,0)\) ⓑ\((8,6)\) ⓒ\((−2,−1)\) ⓓ\((3,4)\) ⓔ\((−1,−4)\)

    Réponse

    ⓐ oui ⓑ oui ⓒ non ⓓ non ⓔ oui

    Reconnaître la relation entre les solutions d'une inégalité et son graphe

    Nous allons maintenant voir comment les solutions d'une inégalité sont liées à son graphe.

    Repensons à la ligne numérique affichée précédemment. Le point\(x=3\) séparait cette ligne numérique en deux parties. Sur un côté de 3 se trouvent tous les nombres inférieurs à 3. De l'autre côté de 3, tous les nombres sont supérieurs à 3. Voir la figure.

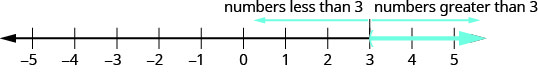
    Image de la ligne numérique avec les nombres entiers de moins 5 à 5. La partie de la ligne numérique située à droite du chiffre 3 est marquée par une ligne bleue. Le chiffre 3 est marqué par une parenthèse ouverte bleue. La partie de la ligne numérique située à droite du chiffre 3 est intitulée « nombres supérieurs à 3 ». La partie de la ligne numérique située à gauche de 3 est intitulée « nombres inférieurs à 3 ».
    Figure\(\PageIndex{2}\) : La solution à\(x>3\) est la partie ombrée de la ligne numérique à droite de\(x=3\).

    De même, la ligne\(y=x+4\) sépare le plan en deux régions. D'un côté de la ligne se trouvent des points avec\(y<x+4\). De l'autre côté de la ligne se trouvent les points avec\(y>x+4\). Nous appelons cette ligne\(y=x+4\) une ligne de démarcation.

    LIGNE DE DÉMARCATION

    La ligne avec équation\(Ax+By=C\) est la ligne de démarcation qui sépare la région où\(Ax+By>C\) de la région où\(Ax+By<C\).

    Pour une inégalité dans une variable, le point de terminaison est indiqué entre parenthèses ou crochets selon que a est inclus ou non dans la solution :

    Deux lignes numériques sont affichées avec le chiffre « a » au milieu. Sur les deux lignes numériques, la partie située à gauche du chiffre a est marquée en rouge. La première ligne numérique est étiquetée « x est inférieur à a » et le chiffre a est marqué par une parenthèse ouverte. La deuxième ligne numérique est étiquetée « x est inférieur ou égal à a » et le chiffre a est marqué par un crochet ouvert.

    De même, pour une inégalité entre deux variables, la ligne de démarcation est représentée par une ligne continue ou pointillée pour indiquer si la ligne est incluse ou non dans la solution.

    \[ \begin{array} {ll} {Ax+By<C} &{Ax+By\leq C} \\ {Ax+By>C} &{Ax+By\geq C} \\ {\text{Boundary line is }Ax+By=C.} &{\text{Boundary line is }Ax+By=C.} \\ {\text{Boundary line is not included in solution.}} &{\text{Boundary line is not included in solution.}} \\ {\textbf{Boundary line is dashed.}} &{\textbf{Boundary line is solid.}} \\ \nonumber \end{array} \]

    Maintenant, regardons ce que nous avons trouvé dans Example. Nous allons commencer par tracer la ligne\(y=x+4\), puis nous allons tracer les cinq points que nous avons testés, comme indiqué sur le graphique. Voir la figure.

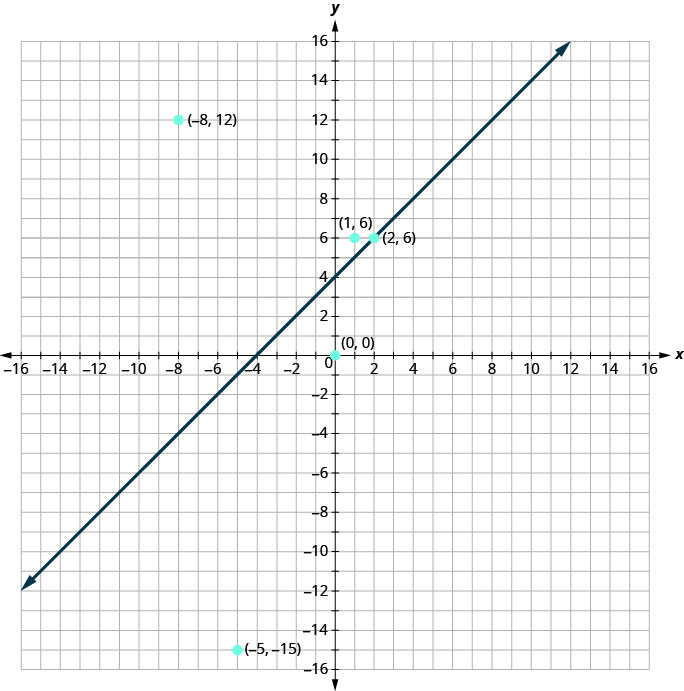
    Cette figure présente le graphique de certains points et d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 16 à 16. Les points (moins 8, 12), (négatif 5, négatif 15), (0, 0), (1, 6) et (2, 6) sont tracés et étiquetés avec leurs coordonnées. Une ligne droite est tracée entre les points (moins 4, 0), (0, 4) et (2, 6).
    Figurine\(\PageIndex{3}\)

    Dans l'exemple, nous avons constaté que certains points étaient des solutions à l'inégalité\(y>x+4\) et d'autres non.

    Parmi les points que nous avons tracés, lesquels constituent des solutions à l'inégalité\(y>x+4\) ?

    Les points\((1,6)\) et\((−8,12)\) sont des solutions à l'inégalité\(y>x+4\). Notez qu'ils se trouvent tous les deux du même côté de la ligne de démarcation\(y=x+4\).

    Les deux points\((0,0)\)\((−5,−15)\) se situent de l'autre côté de la ligne\(y=x+4\) de démarcation et ne constituent pas des solutions à l'inégalité\(y>x+4\). Pour ces deux points,\(y<x+4\).

    Qu'en est-il de ce point\((2,6)\) ? Parce que\(6=2+4\) le point est une solution à l'équation\(y=x+4\), mais pas une solution à l'inégalité\(y>x+4\). Le point\((2,6)\) se trouve donc sur la ligne de démarcation.

    Prenons un autre point au-dessus de la ligne de démarcation et testons s'il s'agit ou non d'une solution à l'inégalité\(y>x+4\). Le point semble\((0,10)\) clairement au-dessus de la ligne de démarcation, n'est-ce pas ? Est-ce une solution à l'inégalité ?

    \[\begin{array} {lll} {y} &{>} &{x+4} \\ {10} &{\overset{?}{>}} &{0+4} \\ {10} &{>} &{4} \\ \nonumber \end{array}\]

    Donc,\((0,10)\) est une solution pour\(y>x+4\).

    Tout point que vous choisissez au-dessus de la ligne de démarcation est une solution à l'inégalité\(y>x+4\). Tous les points au-dessus de la ligne de démarcation sont des solutions.

    De même, tous les points situés sous la ligne de démarcation, du côté avec\((0,0)\) et\((−5,−15)\), ne sont pas des solutions\(y>x+4\), comme le montre la figure.

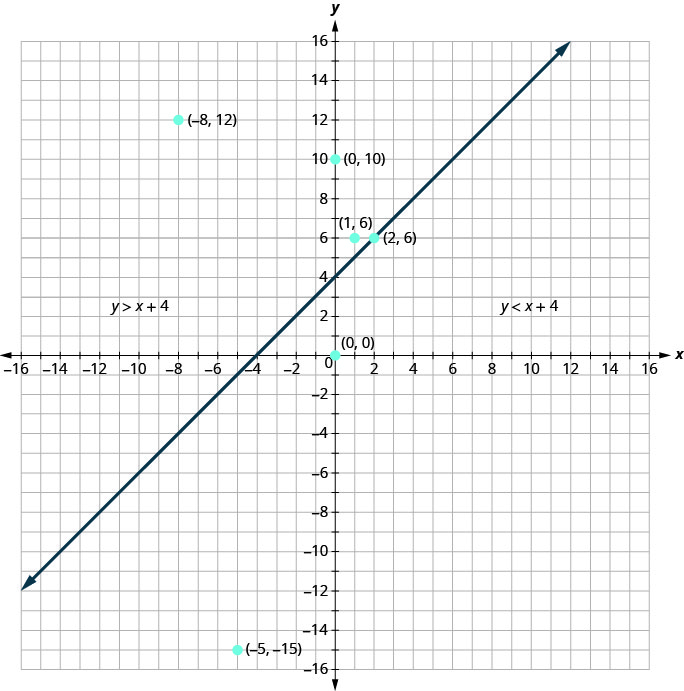
    Cette figure présente le graphique de certains points et d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 16 à 16. Les points (moins 8, 12), (négatif 5, négatif 15), (0, 0), (1, 6) et (2, 6) sont tracés et étiquetés avec leurs coordonnées. Une ligne droite est tracée entre les points (moins 4, 0), (0, 4) et (2, 6). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure gauche est étiquetée y est supérieure à x plus 4. La moitié inférieure droite est étiquetée y est inférieur à x plus 4.
    Figurine\(\PageIndex{4}\)

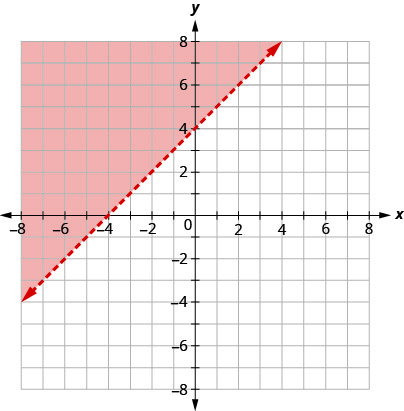
    Le graphique de l'inégalité\(y>x+4\) est présenté ci-dessous.

    La ligne\(y=x+4\) divise le plan en deux régions. La partie ombrée montre les solutions à l'inégalité\(y>x+4\).

    Les points de la ligne de démarcation, ceux où\(y=x+4\), ne sont pas des solutions à l'inégalité\(y>x+4\), de sorte que la ligne elle-même ne fait pas partie de la solution. Nous le montrons en faisant en sorte que la ligne soit pointillée et non pleine.

    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de 8 à 8. Une ligne droite en pointillés est tracée à travers les points (moins 4, 0), (0, 4) et (2, 6). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure gauche est colorée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Exemple\(\PageIndex{4}\)

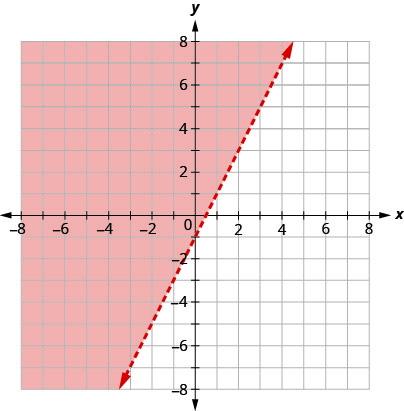
    La ligne de démarcation indiquée sur ce graphique est\(y=2x−1\). Écrivez l'inégalité indiquée par le graphique.

    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de 8 à 8. Une ligne droite pointillée est tracée entre les points (0, moins 1), (1, 1) et (2, 3). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure gauche est colorée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Réponse

    La ligne\(y=2x−1\) est la ligne de démarcation. D'un côté de la ligne se trouvent les points avec\(y>2x−1\) et de l'autre côté de la ligne se trouvent les points avec\(y<2x−1\).

    Testons le point\((0,0)\) et voyons quelle inégalité décrit sa position par rapport à la ligne de démarcation.

    À\((0,0)\), quelle inégalité est vraie :\(y>2x−1\) ou\(y<2x−1\) ?

    \[\begin{array} {ll} {y>2x−1} &{y<2x−1} \\ {0\overset{?}{>}2·0−1} &{0\overset{?}{<}2·0−1} \\ {0>−1\text{ True}} &{0<−1\text{ False}} \\ \nonumber \end{array}\]

    Puisque,\(y>2x−1\) c'est vrai, le côté de la ligne avec\((0,0)\), est la solution. La zone ombrée montre la solution de l'inégalité\(y>2x−1\).

    Comme la ligne de démarcation est représentée par une ligne continue, l'inégalité inclut le signe égal.

    Le graphique montre l'inégalité\(y\geq 2x−1\).

    Nous pouvons utiliser n'importe quel point comme point de test, à condition qu'il ne soit pas sur la ligne. Pourquoi avons-nous choisi\((0,0)\) ? Parce que c'est le plus facile à évaluer. Vous pouvez choisir un point de l'autre côté de la ligne de démarcation et le vérifier\(y<2x−1\).

    Exemple\(\PageIndex{5}\)

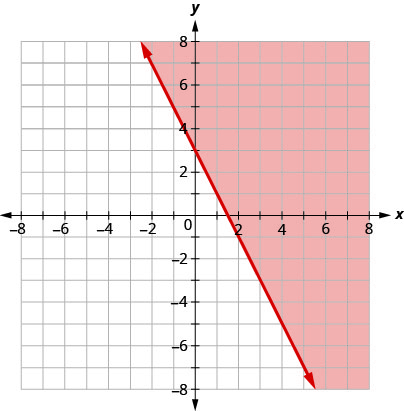
    Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation\(y=−2x+3\).

    Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de 8 à 8. Une ligne droite passe par les points (0, 3), (1, 1) et (3, moins 3). La ligne divise le plan de coordonnées x y en deux moitiés. La ligne elle-même et la moitié supérieure droite sont colorées en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Réponse

    \(y\geq −2x+3\)

    Exemple\(\PageIndex{6}\)

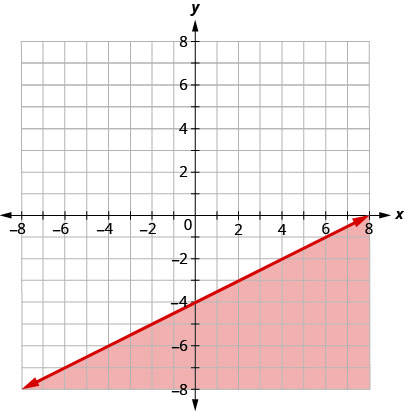
    Écrivez l'inégalité indiquée par le graphique avec la ligne de démarcation\(y=\frac{1}{2}x−4\).

    Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de 8 à 8. Une ligne droite passe par les points (0, moins 4), (2, moins 3) et (4, moins 2). La ligne divise le plan de coordonnées x y en deux moitiés. La ligne elle-même et la moitié inférieure droite sont colorées en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Réponse

    \(y\leq \frac{1}{2}x−4\)

    Exemple\(\PageIndex{7}\)

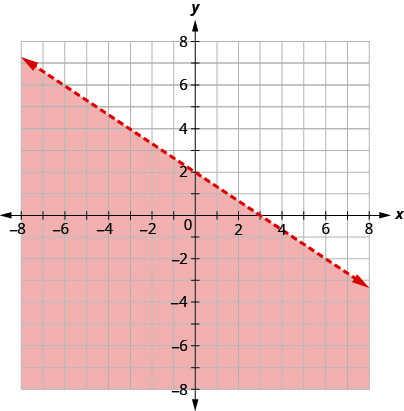
    La ligne de démarcation indiquée sur ce graphique est\(2x+3y=6\). Écrivez l'inégalité indiquée par le graphique.

    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de 8 à 8. Une ligne droite pointillée passe par les points (0, 2), (3, 0) et (6, moins 2). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié inférieure gauche est colorée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Réponse

    La ligne\(2x+3y=6\) est la ligne de démarcation. D'un côté de la ligne se trouvent les points avec\(2x+3y>6\) et de l'autre côté de la ligne se trouvent les points avec\(2x+3y<6\).

    Testons le point\((0,0)\) et voyons quelle inégalité décrit son côté de la ligne de démarcation.

    À\((0,0)\), quelle inégalité est vraie :\(2x+3y>6\) ou\(2x+3y<6\) ?

    \[\begin{array} {ll} {2x+3y>6} &{2x+3y<6} \\ {2(0)+3(0)\overset{?}{>}6} &{2(0)+3(0)\overset{?}{<}6} \\ {0>6\text{ False}} &{0<6\text{ True}} \\ \nonumber \end{array}\]

    Donc, le côté avec\((0,0)\) est le côté où\(2x+3y<6\).

    (Vous pouvez choisir un point de l'autre côté de la ligne de démarcation et le vérifier\(2x+3y>6\).)

    Comme la ligne de démarcation est représentée sous la forme d'une ligne pointillée, l'inégalité n'inclut pas de signe égal.

    La zone ombrée montre la solution à l'inégalité\(2x+3y<6\).

    Exemple\(\PageIndex{8}\)

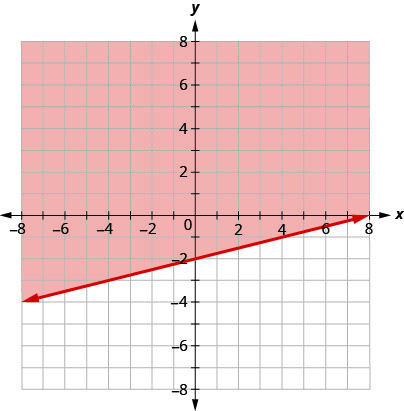
    Écrivez l'inégalité indiquée par la région ombrée dans le graphique avec la ligne de démarcation\(x−4y=8\).

    Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de 8 à 8. Une ligne droite passe par les points (0, moins 2), (4, moins 1) et (8, 0). La ligne divise le plan de coordonnées x y en deux moitiés. La ligne elle-même et la moitié supérieure gauche sont colorées en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Réponse

    \(x−4y\leq 8\)

    Exemple\(\PageIndex{9}\)

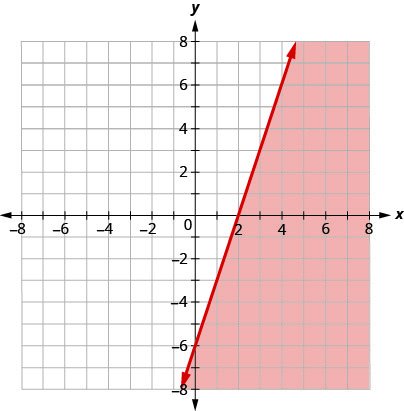
    Écrivez l'inégalité indiquée par la région ombrée dans le graphique avec la ligne de démarcation\(3x−y=6\).

    Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de 8 à 8. Une ligne droite passe par les points (0, moins 6), (1, moins 3) et (2, 0). La ligne divise le plan de coordonnées x y en deux moitiés. La ligne elle-même et la moitié inférieure droite sont colorées en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Réponse

    \(3x−y\geq 6\)

    Représenter graphiquement les inégalités linéaires dans deux variables

    Maintenant que nous savons à quoi ressemble le graphe d'une inégalité linéaire et comment il est lié à une équation limite, nous pouvons utiliser ces connaissances pour représenter graphiquement une inégalité linéaire donnée.

    Exemple\(\PageIndex{10}\): How to Graph a Linear Equation in Two Variables

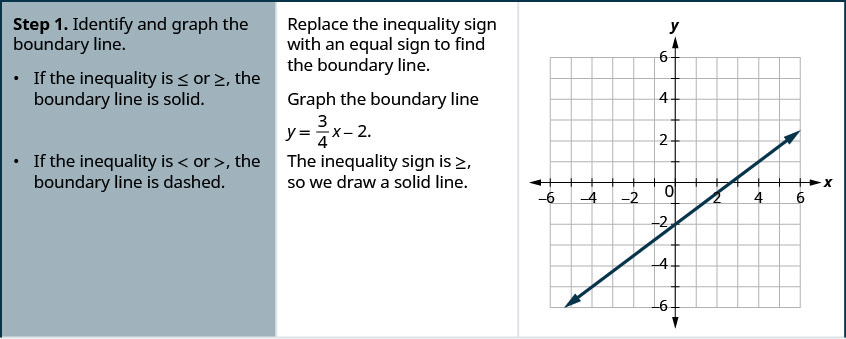
    Tracez l'inégalité linéaire\(y\geq \frac{3}{4}x−2\).

    Réponse

    L'étape 1 consiste à identifier et à tracer la ligne de démarcation. Si l'inégalité est inférieure ou égale, supérieure ou égale, la ligne de démarcation est pleine. Si l'inégalité est inférieure ou supérieure à, la ligne de démarcation est pointillée. Dans cet exemple, le signe d'inégalité est supérieur ou égal, nous dessinons donc une ligne continue. Remplacez le signe d'inégalité par un signe égal pour trouver la limite. Tracez la ligne de démarcation y = 3 divisée par 4 fois x moins 2. La figure montre ensuite le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 12 à 12. La ligne passe par les points (0, moins 2), (4, 1) et (8, 4).L'étape 2 consiste à tester un point qui ne se trouve pas sur la ligne de démarcation. Est-ce une solution à l'inégalité ? Nous allons tester (0, 0). At (0, 0) y est-il supérieur ou égal à 3 divisé par 4 fois x moins 2 ? Est-ce que 0 est supérieur ou égal à 3 divisé par 4 fois 0 moins 2 ? 0 est supérieur ou égal à moins 2, donc (0, 0) est une solution.L'étape 3 consiste à ombrer un côté de la ligne de démarcation. Si le point d'essai est une solution, ombrez le côté qui inclut le point. Si le point d'essai n'est pas une solution, ombrez le côté opposé. Le point de test (0, 0) est une solution à y supérieure ou égale à 3 divisée par 4 fois x moins 2. Nous ombrons donc le côté qui contient (0, 0). La figure montre ensuite le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 12 à 12. La ligne passe par les points (0, moins 2), (4, 1) et (8, 4). La moitié supérieure gauche du plan de coordonnées est ombrée pour indiquer que c'est là que se trouve l'ensemble de solutions.

    Exemple\(\PageIndex{11}\)

    Tracez l'inégalité linéaire\(y>\frac{5}{2}x−4\).

    Réponse

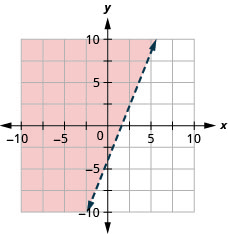
    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de moins 10 à 10. Une ligne droite en pointillés est tracée entre les points (0, moins 4), (2, 1) et (4, 6). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure gauche est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée et de la ligne de démarcation représentent les solutions à\(y>\frac{5}{2}x−4\).

    Exemple\(\PageIndex{12}\)

    Tracez l'inégalité linéaire\(y<\frac{2}{3}x−5\).

    Réponse

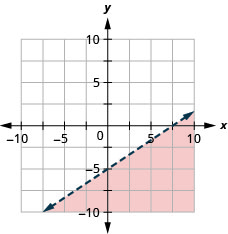
    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de moins 10 à 10. Une ligne droite en pointillés est tracée entre les points (0, moins 5), (3, moins 3) et (5, moins 1). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure gauche est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée, mais pas ceux de la ligne de démarcation, représentent les solutions pour\(y<\frac{2}{3}x−5\).

    Les étapes que nous prenons pour représenter graphiquement une inégalité linéaire sont résumées ici.

    REPRÉSENTEZ GRAPHIQUEMENT UNE INÉGALITÉ LINÉAIRE EN DEUX VARIABLES.
    1. Identifiez et tracez la ligne de démarcation.
      • Si l'inégalité est \ leq ou \ geq, \ leq ou \ geq, la ligne de démarcation est pleine.
      • Si l'inégalité est <or><or>, la ligne de démarcation est pointillée.
    2. Testez un point qui ne se trouve pas sur la ligne de démarcation. Est-ce une solution à l'inégalité ?
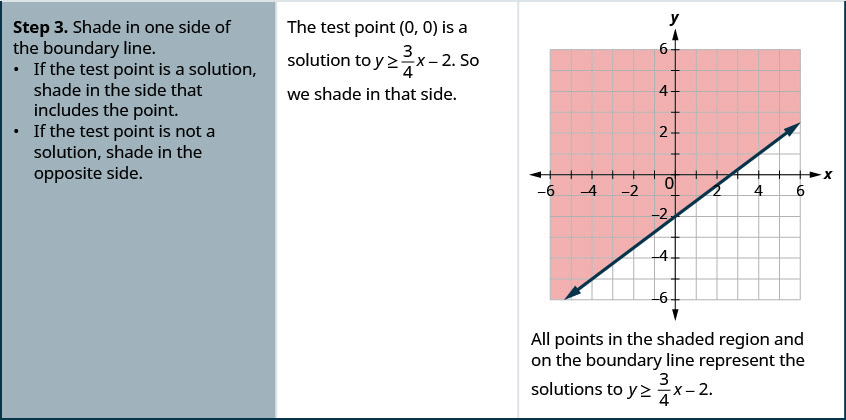
    3. De l'ombre sur un côté de la ligne de démarcation.
      • Si le point d'essai est une solution, ombrez le côté qui inclut le point.
      • Si le point d'essai n'est pas une solution, ombrez le côté opposé.
    Exemple\(\PageIndex{13}\)

    Tracez l'inégalité linéaire\(x−2y<5\).

    Réponse

    Tout d'abord, nous tracons la ligne de démarcation\(x−2y=5\). L'inégalité, c'est\(<\) que nous tracons une ligne pointillée.

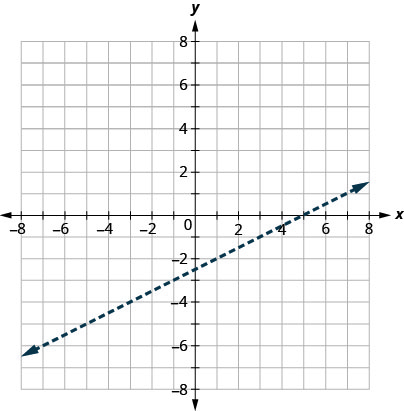
    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de 8 à 8. Une ligne droite en pointillés est tracée entre les points (moins 3, moins 4), (1, moins 2) et (5, 0).

    Ensuite, nous testons un point. Nous l'utiliserons\((0,0)\) à nouveau parce qu'il est facile à évaluer et qu'il ne se trouve pas sur la ligne de démarcation.

    Est-ce\((0,0)\) qu'une solution de\(x−2y<5\) ?

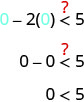
    Est-ce que 0 moins 2 fois 0 est inférieur à 5 ? Est-ce que 0 moins 0 est inférieur à 5 ? 0 est inférieur à 5.

    Le point\((0,0)\) est une solution de\(x−2y<5\), donc nous ombrageons de ce côté de la ligne de démarcation.

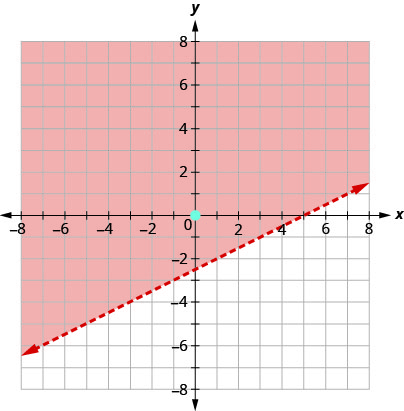
    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de 8 à 8. Une ligne droite en pointillés est tracée entre les points (moins 3, moins 4), (1, moins 2) et (5, 0). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure gauche est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée, mais pas ceux de la ligne de démarcation, représentent les solutions pour\(x−2y<5\).

    Exemple\(\PageIndex{14}\)

    Représentez graphiquement l'inégalité linéaire :\(2x−3y<6\).

    Réponse

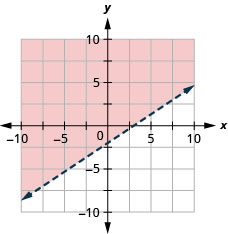
    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de moins 10 à 10. Une ligne droite en pointillés est tracée entre les points (0, moins 2), (3, 0) et (6, 2). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure gauche est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée, mais pas ceux de la ligne de démarcation, représentent les solutions pour\(2x−3y<6\).

    Exemple\(\PageIndex{15}\)

    Représentez graphiquement l'inégalité linéaire :\(2x−y>3\).

    Réponse

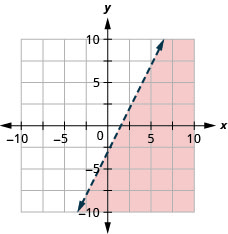
    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de moins 10 à 10. Une ligne droite pointillée est tracée entre les points (0, moins 3), (1, moins 1) et (2, 1). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié inférieure droite est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée, mais pas ceux de la ligne de démarcation, représentent les solutions pour\(2x−y>3\).

    Et si la ligne de démarcation passe par l'origine ? Ensuite, nous ne pourrons pas l'utiliser\((0,0)\) comme point de test. Pas de problème, nous allons simplement choisir un autre point qui ne se trouve pas sur la ligne de démarcation.

    Exemple\(\PageIndex{16}\)

    Représentez graphiquement l'inégalité linéaire :\(y\leq −4x\).

    Réponse

    Tout d'abord, nous tracons la ligne de démarcation\(y=−4x\). Il se présente sous forme de pente et d'interception, avec\(m=−4\) et\(b=0\). L'inégalité, c'est\(\leq\) ainsi que nous tracons une ligne continue.

    Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de 8 à 8. Une ligne droite est tracée entre les points (0, 0), (1, moins 4) et (moins 1, 4).

    Nous avons maintenant besoin d'un point de test. Nous pouvons voir que le point (1,0) (1,0) ne se trouve pas sur la ligne de démarcation.

    Est-ce\((1,0)\) qu'une solution de\(y\leq −4x\) ?

    .

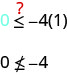
    Le point n'\((1,0)\)étant pas une solution\(y\leq −4x\), nous faisons de l'ombre sur le côté opposé de la ligne de démarcation.

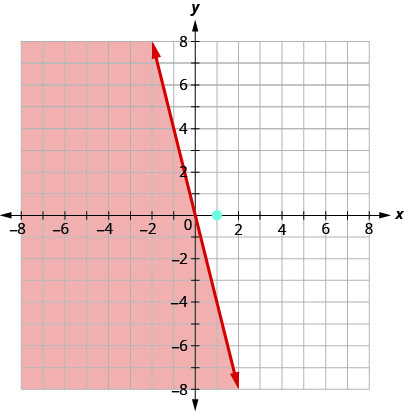
    Est-ce que 0 est inférieur ou égal à moins 4 fois 1 ? 0 n'est pas inférieur ou égal à moins 4.

    Tous les points de la région ombrée et de la ligne de démarcation représentent les solutions à\(y\leq −4x\).

    Exemple\(\PageIndex{17}\)

    Représentez graphiquement l'inégalité linéaire :\(y>−3x\).

    Réponse

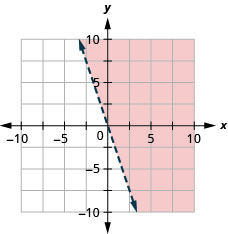
    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de moins 10 à 10. Une ligne droite pointillée est tracée entre les points (moins 1, 3), (0, 0) et (1, moins 3). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure droite est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée, mais pas ceux de la ligne de démarcation, représentent les solutions pour\(y>−3x\).

    Exemple\(\PageIndex{18}\)

    Représentez graphiquement l'inégalité linéaire :\(y\geq −2x\).

    Réponse

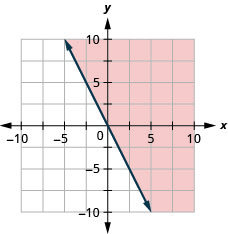
    Cette figure présente le graphique d'une ligne droite pointillée sur le plan de coordonnées x y. Les axes x et y vont de moins 10 à 10. Une ligne droite en pointillés est tracée entre les points (moins 1, 2), (0, 0) et (1, moins 2). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure droite est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée et de la ligne de démarcation représentent les solutions à\(y\geq −2x\).

    Certaines inégalités linéaires ne comportent qu'une seule variable. Ils peuvent avoir un x mais pas de y, ou un y mais pas de x. Dans ces cas, la ligne de démarcation sera verticale ou horizontale.

    Rappelons que :

    \[\begin{array} {ll} {x=a} &{\text{vertical line}} \\ {y=b} &{\text{horizontal line}} \\ \nonumber \end{array}\]

    Exemple\(\PageIndex{19}\)

    Représentez graphiquement l'inégalité linéaire :\(y>3\).

    Réponse

    Tout d'abord, nous tracons la ligne de démarcation\(y=3\). Il s'agit d'une ligne horizontale. L'inégalité, c'est\(>\) que nous tracons une ligne pointillée.

    Nous testons ce point\((0,0)\).

    \[y>3\nonumber\]\[0\slashed{>}3\nonumber\]

    Donc, n'\((0,0)\)est pas une solution à\(y>3\).

    Nous ombrons donc le côté qui n'inclut pas\((0,0)\), comme indiqué sur ce graphique.

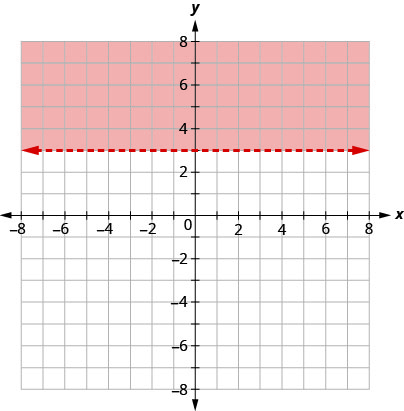
    Cette figure présente le graphique d'une ligne pointillée horizontale droite sur le plan de coordonnées x. Les axes x et y vont de 8 à 8. Une ligne pointillée horizontale est tracée à travers les points (moins 1, 3), (0, 3) et (1, 3). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié supérieure est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée, mais pas ceux de la ligne de démarcation, représentent les solutions pour\(y>3\).

    Exemple\(\PageIndex{20}\)

    Représentez graphiquement l'inégalité linéaire :\(y<5\).

    Réponse

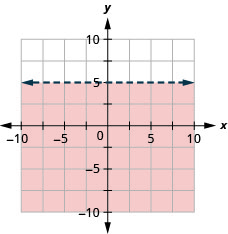
    Cette figure présente le graphique d'une ligne pointillée horizontale droite sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. Une ligne pointillée horizontale est tracée à travers les points (moins 1, 5), (0, 5) et (1, 5). La ligne divise le plan de coordonnées x y en deux moitiés. La moitié inférieure est ombrée en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée, mais pas ceux de la ligne de démarcation, représentent les solutions pour\(y<5\).

    Exemple\(\PageIndex{21}\)

    Représentez graphiquement l'inégalité linéaire :\(y\leq −1\).

    Réponse

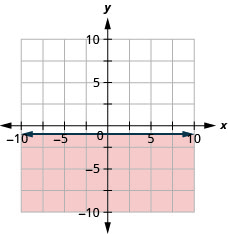
    Cette figure montre le graphique d'une ligne horizontale droite sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. Une ligne horizontale est tracée entre les points (négatif 1, négatif 1), (0, négatif 1) et (1, négatif 1). La ligne divise le plan de coordonnées x y en deux moitiés. La ligne et la moitié inférieure sont ombrées en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    Tous les points de la région ombrée et de la ligne de démarcation représentent les solutions à\(y\leq −1\).

    Résolvez des applications en utilisant des inégalités linéaires dans deux variables

    De nombreux domaines utilisent des inégalités linéaires pour modéliser un problème. Bien que nos exemples puissent porter sur des situations simples, ils nous donnent l'occasion de renforcer nos compétences et de nous faire une idée de la façon dont elles pourraient être utilisées.

    Exemple\(\PageIndex{22}\)

    Hilaria occupe deux emplois à temps partiel afin de gagner suffisamment d'argent pour s'acquitter de ses obligations d'au moins 240$ par semaine. Son travail dans la restauration rapporte 10 dollars de l'heure et son travail de tutorat sur le campus rapporte 15 dollars de l'heure. Combien d'heures Hilaria doit-elle travailler pour chaque emploi pour gagner au moins 240$ ?

    ⓐ Soit xx le nombre d'heures pendant lesquelles elle travaille dans le secteur de la restauration et y le nombre d'heures pendant lesquelles elle donne des cours particuliers. Écrivez une inégalité qui modéliserait cette situation.

    ⓑ Représentez graphiquement l'inégalité

    ⓒ Trouvez trois paires ordonnées\((x,y)\) qui seraient des solutions à l'inégalité. Ensuite, expliquez ce que cela signifie pour Hilaria.

    Réponse

    ⓐ On laisse x le nombre d'heures qu'elle travaille dans le secteur de la restauration et y le nombre d'heures pendant lesquelles elle donne des cours particuliers.

    Elle gagne 10$ de l'heure au travail dans la restauration et 15$ de l'heure en tutorat. Pour chaque emploi, le nombre d'heures multiplié par le salaire horaire donnera le montant gagné à cet emploi.

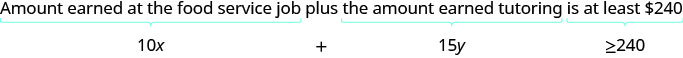
    10 x plus 15 y est supérieur à 240. Le « 10 x » est étiqueté « Montant gagné au travail dans la restauration ». Le « 15 ans » est étiqueté « le montant gagné en tutorat ». La mention « est supérieure à 240 » est étiquetée « est d'au moins 240 ».

    ⓑ Pour représenter graphiquement l'inégalité, nous l'avons présentée sous forme de pente et d'intersection.

    \[\begin{align} {10x+15y} &\geq 240 \\ 15y &\geq -10x+240 \\ y &\geq {−\frac{2}{3}x+16} \\ \nonumber \end{align}\]

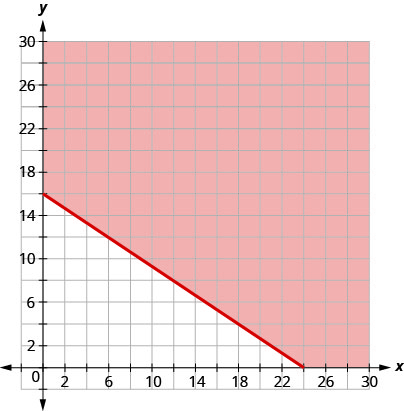
    Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de 0 à 25. Une ligne passe par les points (0, 16), (15, 6) et (24, 0). La ligne divise le plan de coordonnées x y en deux moitiés. La ligne et la moitié supérieure droite sont ombrées en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    ⓒ Sur le graphique, nous voyons que les paires\((15,10)\) ordonnées\((24,0)\) représentent trois solutions parmi une infinité de solutions.\((0,16)\) Vérifiez les valeurs de l'inégalité.

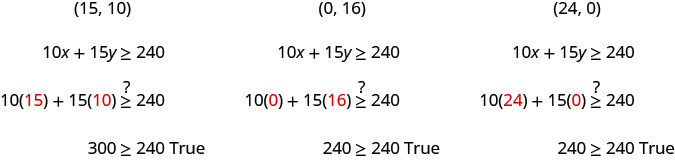
    Nous testons d'abord le point (15, 10) de l'inégalité 10 x plus 15 y supérieure ou égale à 240. Est-ce que 10 fois 15 plus 15 fois 10 sont supérieurs ou égaux à 240 ? Puisque 300 est supérieur ou égal à 240 (15, 10) est une solution. Ensuite, nous testons le point (0, 16) de l'inégalité 10 x plus 15 y supérieure ou égale à 240. Est-ce que 10 fois 0 plus 15 fois 16 sont supérieurs ou égaux à 240 ? Puisque 240 est supérieur ou égal à 240 (0, 16) est une solution. Ensuite, nous testons le point (24, 0) de l'inégalité 10 x plus 15 y supérieure ou égale à 240. Est-ce que 10 fois 24 plus 15 fois 0 sont supérieurs ou égaux à 240 ? Comme 240 est supérieur ou égal à 240 (24, 0), c'est une solution.

    Pour Hilaria, cela signifie que pour gagner au moins 240$, elle peut travailler 15 heures de tutorat et 10 heures à son travail de restauration rapide, gagner tout son argent en faisant du tutorat pendant 16 heures ou gagner tout son argent en travaillant 24 heures sur 24 dans le secteur de la restauration.

    Exemple\(\PageIndex{23}\)

    Hugh occupe deux emplois à temps partiel. L'un dans une épicerie qui paie 10 dollars de l'heure et l'autre fait du baby-sitting pour 13 dollars de l'heure. Entre les deux emplois, Hugh veut gagner au moins 260$ par semaine. Combien d'heures Hugh doit-il travailler pour chaque emploi pour gagner au moins 260$ ?

    ⓐ Soit x le nombre d'heures pendant lesquelles il travaille à l'épicerie et y le nombre d'heures pendant lesquelles il fait du baby-sitting. Écrivez une inégalité qui modéliserait cette situation.

    ⓑ Représentez graphiquement l'inégalité

    ⓒ Trouvez trois paires ordonnées (x, y) qui seraient des solutions à l'inégalité. Ensuite, expliquez ce que cela signifie pour Hugh.

    Réponse

    ⓐ\(10x+13y\geq 260\)
    ⓑ

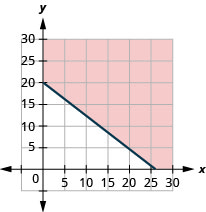
    Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de 0 à 30. Une ligne passe par les points (0, 20), (13, 10) et (26, 0). La ligne divise le plan de coordonnées x y en deux moitiés. La ligne et la moitié supérieure droite sont ombrées en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    ⓒ Les réponses peuvent varier.

    Exemple\(\PageIndex{24}\)

    Veronica occupe deux emplois à temps partiel afin de gagner suffisamment d'argent pour s'acquitter de ses obligations d'au moins 280$ par semaine. Son travail au spa de jour rapporte 10 dollars de l'heure et son emploi d'assistante administrative sur le campus rapporte 17,50 dollars de l'heure. Combien d'heures Veronica doit-elle travailler pour chaque emploi pour gagner au moins 280$ ?

    ⓐ Soit x le nombre d'heures pendant lesquelles elle travaille au spa de jour et y le nombre d'heures pendant lesquelles elle travaille en tant qu'assistante administrative. Écrivez une inégalité qui modéliserait cette situation.

    ⓑ Représentez graphiquement l'inégalité

    ⓒ Trouvez trois paires ordonnées (x, y) qui seraient des solutions à l'inégalité. Ensuite, expliquez ce que cela signifie pour Veronica

    Réponse

    ⓐ\(10x+17.5y\geq 280\)
    ⓑ

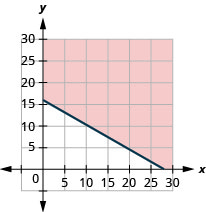
    Cette figure montre le graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de 0 à 25. Une ligne est tracée entre les points (0, 16) et (28, 0). La ligne divise le plan de coordonnées x y en deux moitiés. La ligne et la moitié supérieure droite sont ombrées en rouge pour indiquer que c'est là que se trouvent les solutions à l'inégalité.

    ⓒ Les réponses peuvent varier.

    Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur la représentation graphique des inégalités linéaires en deux variables.

    Concepts clés

    • Comment représenter graphiquement une inégalité linéaire entre deux variables.
      1. Identifiez et tracez la ligne de démarcation.
        Si l'inégalité est\(\leq\) ou\(\geq\), la ligne de démarcation est pleine.
        Si l'inégalité est\(<\) ou\(>\), la ligne de démarcation est pointillée.
      2. Testez un point qui ne se trouve pas sur la ligne de démarcation. Est-ce une solution à l'inégalité ?
      3. De l'ombre sur un côté de la ligne de démarcation.
        Si le point d'essai est une solution, ombrez le côté qui inclut le point.
        Si le point d'essai n'est pas une solution, ombrez le côté opposé.

    Lexique

    ligne de démarcation
    La ligne avec équation\(Ax+By=C\) est la ligne de démarcation qui sépare la région où\(Ax+By>C\) de la région où\(Ax+By<C\).
    inégalité linéaire
    Une inégalité linéaire est une inégalité qui peut être écrite sous l'une des formes suivantes :\(Ax+By>C\),,\(Ax+By\geq C\), ou\(Ax+By<C\)\(Ax+By\leq C\), où A et B ne sont pas tous deux nuls.
    solution à une inégalité linéaire
    Une paire ordonnée\((x,y)\) est une solution à une inégalité linéaire si l'inégalité est vraie lorsque nous substituons les valeurs de x et de y.