3.4E : Exercices

Last updated
Save as PDF

Page ID: 194121

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La pratique rend la perfection

Trouvez une équation de la droite en fonction de la pente et de l'intersection y

Dans les exercices suivants, trouvez l'équation d'une droite avec une pente et une intersection y données. Écrivez l'équation sous forme d'intersection de pente.

1. pente$3$ et$y$ intersection$(0,5)$

Réponse: $y=3x+5$

2. pente$8$ et$y$ intersection$(0,−6)$

3. pente$−3$ et$y$ intersection$(0,−1)$

Réponse: $y=−3x−1$

4. pente$−1$ et$y$ intersection$(0,3)$

5. pente$\frac{1}{5}$ et$y$ intersection$(0,−5)$

Réponse: $y=\frac{1}{5}x−5$

6. pente$−\frac{3}{4}$ et$y$ intersection$(0,−2)$

7. pente$0$ et$y$ intersection$(0,−1)$

Réponse: $y=−1$

8. pente$−4$ et$y$ intersection$(0,0)$

Dans les exercices suivants, trouvez l'équation de la droite affichée sur chaque graphique. Écrivez l'équation sous forme d'intersection de pente.

9.
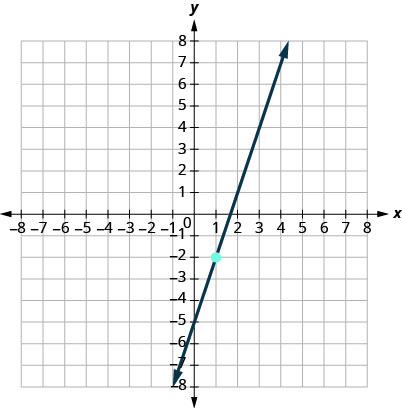
$Cette figure présente un graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. La ligne passe par les points (0, moins 5), (1, moins 2) et (2, 1).$

Réponse: $y=3x−5$

10.
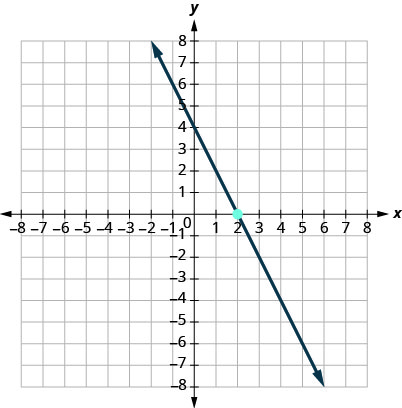
$Cette figure présente un graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. La ligne passe par les points (0, 4), (1, 2) et (2, 0).$

11.
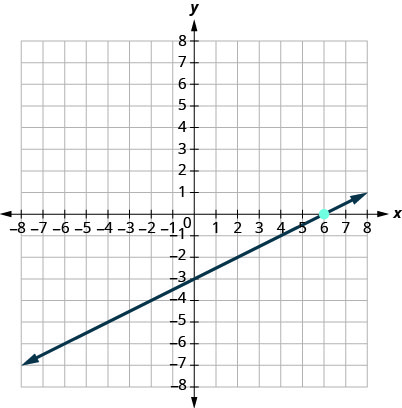
$Cette figure présente un graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. La ligne passe par les points (0, moins 3), (2, moins 2) et (6, 0).$

Réponse: $y=\frac{1}{2}x−3$

12.
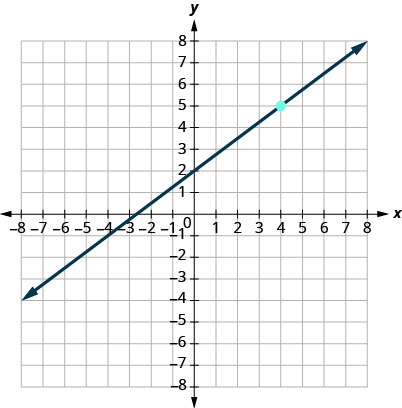
$Cette figure présente un graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. La ligne passe par les points (0, 2), (4, 5) et (8, 8).$

13.
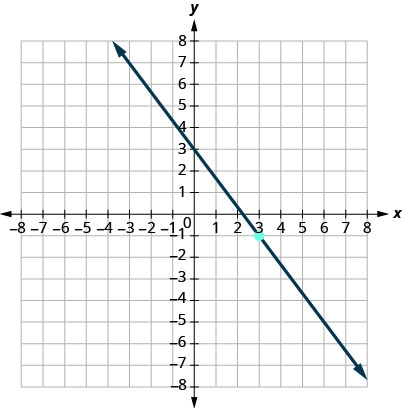
$Cette figure présente un graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. La ligne passe par les points (0, 3), (3, moins 1) et (6, moins 5).$

Réponse: $y=−\frac{4}{3}x+3$

14.
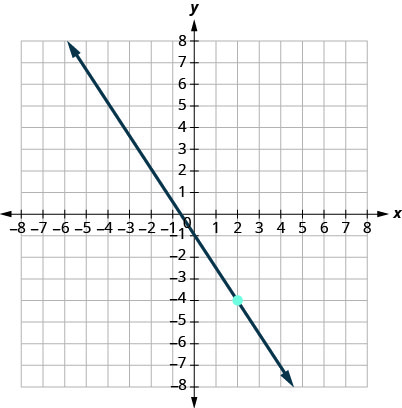
$Cette figure présente un graphique d'une ligne droite sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. La ligne passe par les points (0, moins 1), (2, moins 4) et (4, moins 7).$

15.
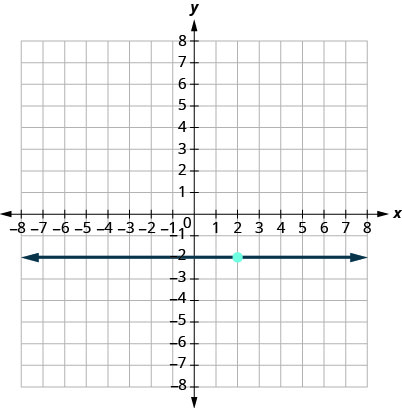
$Cette figure montre un graphique d'une ligne droite horizontale sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. La ligne passe par les points (0, moins 2), (1, moins 2) et (2, moins 2).$

Réponse: $y=−2$

16.
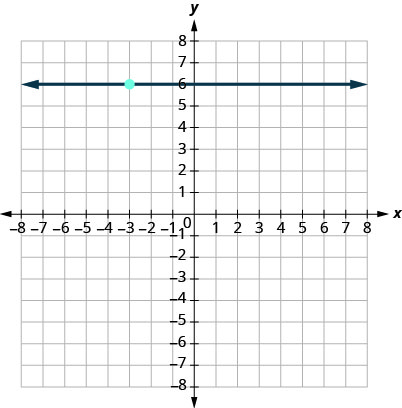
$Cette figure montre un graphique d'une ligne droite horizontale sur le plan de coordonnées x. Les axes x et y vont de moins 10 à 10. La ligne passe par les points (0, 6), (1, 6) et (2, 6).$

Trouvez une équation de la droite en fonction de la pente et d'un point

Dans les exercices suivants, trouvez l'équation d'une droite avec une pente donnée et contenant le point donné. Écrivez l'équation sous forme d'intersection de pente.

17. $m=\frac{5}{8}$, point$(8,3)$

Réponse: $y=\frac{5}{8}x−2$

18. $m=\frac{5}{6}$, point$(6,7)$

19. $m=−\frac{3}{5}$, point$(10,−5)$

Réponse: $y=−\frac{3}{5}x+1$

20. $m=−\frac{3}{4}$, point$(8,−5)$

21. $m=−\frac{3}{2}$, point$(−4,−3)$

Réponse: $y=−\frac{3}{2}x+9$

22. $m=−\frac{5}{2}$, point$(−8,−2)$

23. $m=−7$, point$(−1,−3)$

Réponse: $y=−7x−10$

24. $m=−4$, point$(−2,−3)$

25. Ligne horizontale contenant$(−2,5)$

Réponse: $y=5$

26. Ligne horizontale contenant$(−2,−3)$

27. Ligne horizontale contenant$(−1,−7)$

Réponse: $y=−7$

28. Ligne horizontale contenant$(4,−8)$

Trouvez une équation de la droite à partir de deux points

Dans les exercices suivants, trouvez l'équation d'une droite contenant les points donnés. Écrivez l'équation sous forme d'intersection de pente.

29. $(2,6)$et$(5,3)$

Réponse: $y=−x+8$

30. $(4,3)$et$(8,1)$

31. $(−3,−4)$et$(5−2)$.

Réponse: $y=\frac{1}{4}x−\frac{13}{4}$

32. $(−5,−3)$et$(4,−6)$.

33. $(−1,3)$et$(−6,−7)$.

Réponse: $y=2x+5$

34. $(−2,8)$et$(−4,−6)$.

35. $(0,4)$et$(2,−3)$.

Réponse: $y=−\frac{7}{2}x+4$

36. $(0,−2)$et$(−5,−3)$.

37. $(7,2)$et$(7,−2)$.

Réponse: $x=7$

38. $(−2,1)$et$(−2,−4)$.

39. $(3,−4)$et$(5,−4)$.

Réponse: $y=−4$

40. $(−6,−3)$et$(−1,−3)$

Trouver l'équation d'une droite parallèle à une droite donnée

Dans les exercices suivants, trouvez l'équation d'une droite parallèle à la droite donnée et contenant le point donné. Écrivez l'équation sous forme d'intersection de pente.

41. Ligne$y=4x+2$, point$(1,2)$

Réponse: $y=4x−2$

42. ligne$y=−3x−1$, point$2,−3)$.

43. ligne$2x−y=6$, point$(3,0)$.

Réponse: $y=2x−6$

44. ligne$2x+3y=6$, point$(0,5)$.

45. ligne$x=−4$, point$(−3,−5)$.

Réponse: $x=−3$

46. ligne$x−2=0$, point$(1,−2)$

47. ligne$y=5$, point$(2,−2)$

Réponse: $y=−2$

48. ligne$y+2=0$, point$(3,−3)$

Trouver l'équation d'une droite perpendiculaire à une droite donnée

Dans les exercices suivants, trouvez l'équation d'une droite perpendiculaire à la droite donnée et contenant le point donné. Écrivez l'équation sous forme d'intersection de pente.

49. ligne$y=−2x+3$, point$(2,2)$

Réponse: $y=\frac{1}{2}x+1$

50. ligne$y=−x+5$, point$(3,3)$

51. Ligne$y=\frac{3}{4}x−2$, point$(−3,4)$

Réponse: $y=−\frac{4}{3}x$

52. ligne$y=\frac{2}{3}x−4$, point$(2,−4)$

53. ligne$2x−3y=8$, point$(4,−1)$

Réponse: $y=−\frac{3}{2}x+5$

54. ligne$4x−3y=5$, point$(−3,2)$

55. ligne$2x+5y=6$, point$(0,0)$

Réponse: $y=\frac{5}{2}x$

56. ligne$4x+5y=−3$, point$(0,0)$

57. ligne$x=3$, point$(3,4)$

Réponse: $y=4$

58. ligne$x=−5$, point$(1,−2)$

59. ligne$x=7$, point$(−3,−4)$

Réponse: $y=−4$

60. ligne$x=−1$, point$(−4,0)$

61. ligne$y−3=0$, point$(−2,−4)$

Réponse: $x=−2$

62. Ligne$y−6=0$, point$(−5,−3)$

63.$y$ axe de la ligne, point$(3,4)$

Réponse: $y=4$

64.$y$ axe de la ligne, point$(2,1)$

Pratique mixte

Dans les exercices suivants, trouvez l'équation de chaque droite. Écrivez l'équation sous forme d'intersection de pente.

65. Contenant les points$(4,3)$ et$(8,1)$

Réponse: $y=−\frac{1}{2}x+5$

66. Contenant les points$(−2,0)$ et$(−3,−2)$

67. $m=\frac{1}{6}$, contenant un point$(6,1)$

Réponse: $y=\frac{1}{6}x$

68. $m=\frac{5}{6}$, contenant un point$(6,7)$

69. Parallèle à la ligne$4x+3y=6$, contenant le point$(0,−3)$

Réponse: $y=−\frac{4}{3}x−3$

70. Parallèle à la ligne$2x+3y=6$, contenant le point$(0,5)$

71. $m=−\frac{3}{4}$, contenant un point$(8,−5)$

Réponse: $y=−\frac{3}{4}x+1$

72. $m=−\frac{3}{5}$, contenant un point$(10,−5)$

73. Perpendiculaire à la ligne$y−1=0$, point$(−2,6)$

Réponse: $x=−2$

74. Perpendiculaire à l'axe y de la ligne, point$(−6,2)$

75. Parallèle à la ligne$x=−3$, contenant le point$(−2,−1)$

Réponse: $x=−2$

76. Parallèle à la ligne$x=−4$, contenant le point$(−3,−5)$

77. Contenant les points$(−3,−4)$ et$(2,−5)$

Réponse: $y=−\frac{1}{5}x−\frac{23}{5}$

78. Contenant les points$(−5,−3)$ et$(4,−6)$

79. Perpendiculaire à la ligne$x−2y=5$, point$(−2,2)$

Réponse: $y=−2x−2$

80. Perpendiculaire à la ligne$4x+3y=1$, point$(0,0)$

Exercices d'écriture

81. Pourquoi toutes les lignes horizontales sont-elles parallèles ?

Réponse: Les réponses peuvent varier.

82. Expliquez avec vos propres mots pourquoi les pentes de deux lignes perpendiculaires doivent avoir des signes opposés.

Auto-vérification

a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

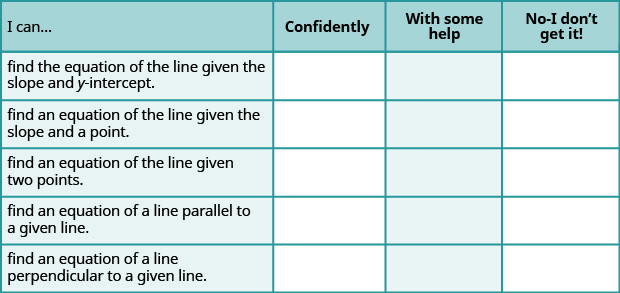
$La figure montre un tableau à six lignes et quatre colonnes. La première ligne est une ligne d'en-tête et elle étiquette chaque colonne. L'en-tête de la première colonne est « Je peux... », le second est « En toute confiance », le troisième est « avec de l'aide », « non moins, je ne comprends pas ! ». Sous la première colonne se trouvent les phrases « trouver l'équation de la droite en fonction de la pente et de l'intersection y », « trouver une équation de la droite en fonction de la pente et d'un point », « trouver une équation de la droite en fonction de deux points », « trouver l'équation d'une droite parallèle à une ligne donnée » et « trouver l'équation d'une droite perpendiculaire » vers une ligne donnée ». Sous les deuxième, troisième et quatrième colonnes se trouvent des espaces vides où l'apprenant peut vérifier le niveau de maîtrise qu'il a atteint.$

b. Que vous indique cette liste de contrôle sur votre maîtrise de cette section ? Quelles mesures allez-vous prendre pour vous améliorer ?