5.3: 人口增长与监管
- Page ID
- 173148
人口生态学家利用各种方法对种群动态进行建模。 准确的模型应该能够描述人口中发生的变化并预测未来的变化。 两个最简单的人口增长模型使用确定性方程(不考虑随机事件的方程)来描述人口规模随时间推移的变化率。 这些模型中的第一个模型是指数增长,它描述了数量增长而不受任何增长限制的人口。 第二种模式是逻辑增长,它引入了生殖增长的极限,随着人口规模的增加,生殖增长变得越来越强烈。 这两个模型都没有充分描述自然种群,但它们提供了比较点。
人口增长率 (r)
人口增长率(有时称为增长率或人均增长率,r)等于出生率(b)减去死亡率(d)除以初始人口规模(N 0)。
计算人口增长率的另一种方法涉及最终和初始人口规模(图\(\PageIndex{a}\))。 在这种情况下,人口增长率 (r) 等于最终人口规模 (N) 减去初始人口规模 (N 0),然后除以初始人口规模 (N 0)。

加倍时间
翻倍时间是指人口达到其初始规模的两倍需要多长时间。 倍增时间 (t) 等于 0.69 除以人口增长率 (r),以比例写成。
人口生态学家有时会绕过这个方程式,使用 “70法则”(将70 除以人口增长率,以百分比表示)计算倍增时间。 要将人口增长率表示为百分比,请将其乘以 100%。 因此,原始倍增时间方程中的 0.69 也乘以 100。 为简单起见,该值 (69) 四舍五入为 70。
指数级增长
查尔斯·达尔文在发展自然选择理论时受到了英国神职人员托马斯·马尔萨斯的影响。 马尔萨斯于 1798 年出版了他的著作,指出拥有丰富自然资源的人口增长非常迅速。 但是,它们消耗了资源,从而限制了进一步的增长。 人口规模加速的早期模式称为指数增长(图\(\PageIndex{b}\))。
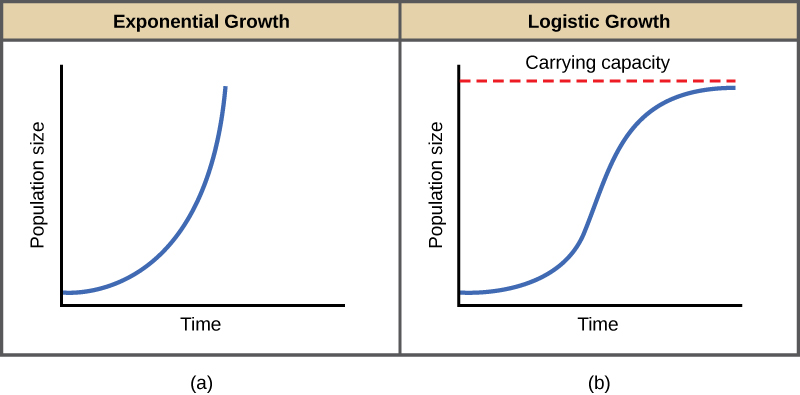
生物体呈指数增长的最好例子是细菌。 细菌是快速繁殖的原核生物,许多物种大约需要一个小时才能繁殖。 如果将1000个细菌放在一个有充足营养供应的大瓶中(这样营养素就不会很快耗尽),那么仅仅一个小时后,细菌的数量就会翻一番,从1000个增加到2000个(图\(\PageIndex{c}\))。 再过一个小时,2000个细菌中的每一个都会分裂,产生4000个细菌。 第三个小时后,烧瓶中应该有 8000 个细菌。 指数增长的重要概念是,生长速度(每个繁殖世代中添加的生物数量)本身正在增加;也就是说,种群规模正在以越来越快的速度增加。 经过其中的24个周期,细菌数量将从1000个增加到超过160亿。 当绘制一段时间内的人口规模 N 时,会产生 J 形的增长曲线(图\(\PageIndex{b}\))。

瓶中细菌的例子并不能真正代表资源通常有限的现实世界。 但是,当一个物种被引入它认为合适的新栖息地时,它可能会在一段时间内呈指数级增长。 就烧瓶中的细菌而言,有些细菌会在实验过程中死亡,因此无法繁殖;因此,生长速度从没有死亡的最大速率降低。
物流增长
只有当无限的自然资源可用时,才有可能实现持续的指数增长;在现实世界中情况并非如此。 查尔斯·达尔文在他对 “生存斗争” 的描述中承认了这一事实,该描述指出,个人将与自己或其他物种的成员争夺有限的资源。 成功的人更有可能存活下来,并以更快的速度将使他们成功的特征传给下一代(自然选择)。 为了模拟资源有限的现实,人口生态学家开发了逻辑增长模型。
在现实世界中,资源有限,指数级增长不可能无限期地持续下去。 在个人很少且资源充足的环境中可能会出现指数级增长,但是当个人数量变得足够多时,资源就会耗尽,增长速度将放缓。 最终,增长率将稳定或趋于平稳(图\(\PageIndex{b}\))。 这种人口规模由特定环境所能承受的最大人口规模决定,称为承载能力,符号为 K。 在实际人口中,不断增长的人口往往超过其承载能力,死亡率的增加超过出生率,导致人口规模下降到承载能力或低于承受能力。 大多数人口通常以起伏的方式围绕承载能力波动,而不是直接存在。
逻辑增长图形生成了 S 形曲线(图\(\PageIndex{b}\))。 这是比指数增长更现实的人口增长模型。 S 形曲线有三个不同的部分。 最初,增长呈指数级增长,因为可用的人很少,资源充足。 然后,随着资源开始变得有限,增长率降低。 最后,增长率在环境的承载能力上趋于平稳,随着时间的推移,人口数量变化不大。
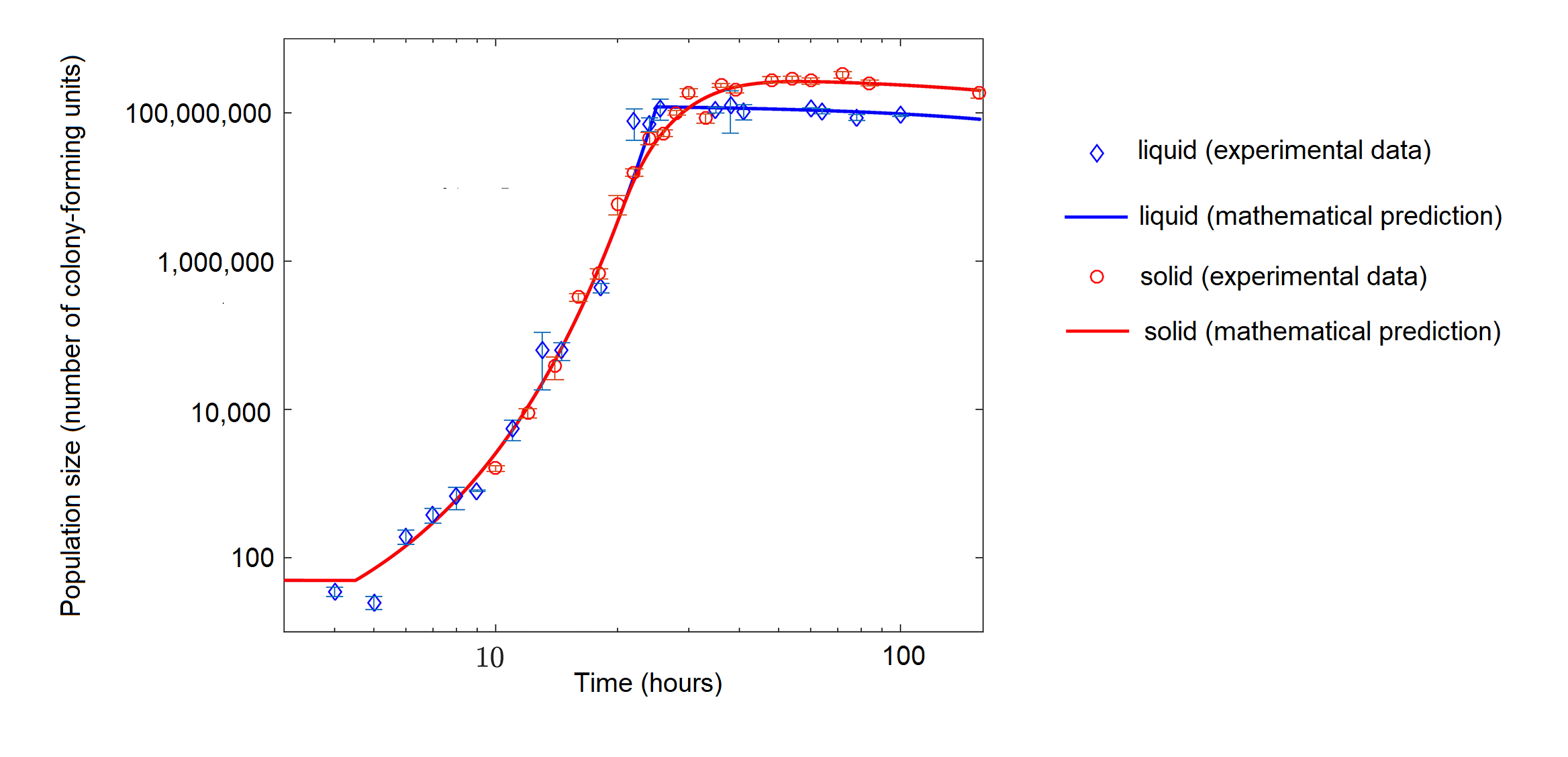
虽然装在富含营养的烧瓶中的细菌最初可能呈指数级增长,但养分有限的细菌可以表现出逻辑生长(图\(\PageIndex{d}\))。
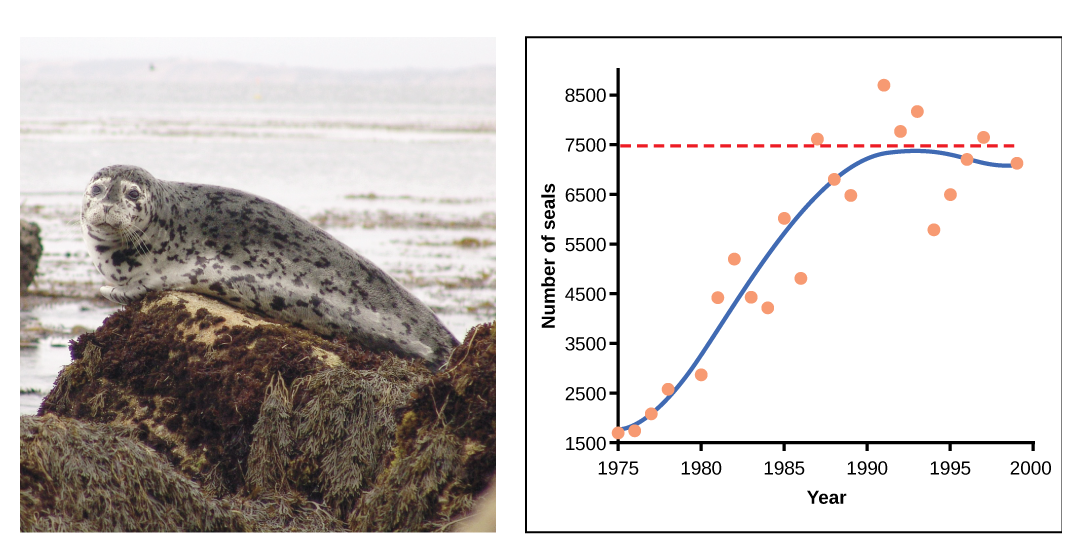
在某些人群中,S 形曲线存在变化。 野生种群中的例子包括绵羊和海豹(图\(\PageIndex{e}\))。 在这两个例子中,人口规模在短时间内超过承载能力,然后降至承载能力以下。 随着人口围绕其承载能力波动,人口规模的这种波动继续发生。 尽管如此,即使出现了这种振荡,逻辑模型还是得到了证实。
逻辑人口增长模型并不是人口对有限资源做出反应的唯一途径。 在某些人群中,增长呈指数级增长,直到资源枯竭、废物积聚或疾病蔓延(见下面的限制因素),然后人口崩溃。 因此,人口增长率(和规模)可能会迅速暴跌,而不是在接近承载能力时逐渐减少。
人口动态与调节
人口增长的逻辑模型虽然在许多自然种群中有效,也是一个有用的模型,但它是对现实世界人口动态的简化。 模型中隐含的是,环境的承载能力没有变化,事实并非如此。 承载能力每年都有所不同。 例如,有些夏季炎热干燥,而另一些则寒冷潮湿;在许多地区,冬季的承载能力远低于夏季。 此外,一些因素(增长因素)提高了人口增长率,而其他因素(限制因素)则减缓了人口增长。 生长因子的例子是食物、水和空间等资源。 限制因素可以分为密度依赖或与密度无关。
密度依赖性调节
大多数密度依赖因素本质上是生物学的(生物的)。 通常,人口越密集,其死亡率就越高。 图\(\PageIndex{f}\)中显示了密度依赖性调节的一个例子,该研究的结果来自一项针对人类和其他哺乳动物的寄生虫(Ascaris lumbricoides)的研究结果。 较密集的寄生虫种群表现出较低的生殖力:它们所含的卵较少。 对此的一种可能的解释是,在较密集的种群中,雌性会较小(由于资源有限),而较小的雌性的卵子会更少。 这一假设在2009年的一项研究中得到了检验和反驳,该研究表明女性的体重没有影响。 该生物体中生殖密度依赖的实际原因尚不清楚,有待进一步调查。
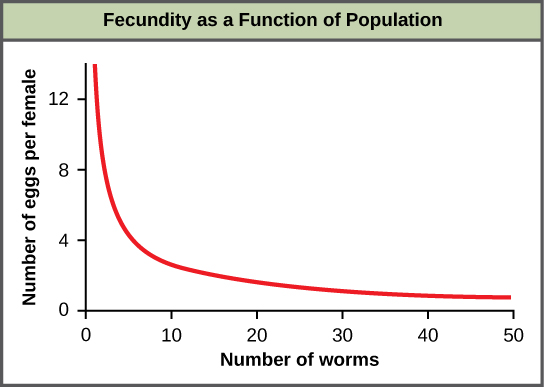
密度依赖因素包括捕食、寄生、草药象牙、竞争和废物积累。 随着种群的增加,它的捕食者能够更轻松地捕获它。 猎物密度也会影响捕食者的种群增长率:猎物密度低会增加捕食者的死亡率,因为它更难找到食物来源。
随着宿主种群密度的增加,寄生虫能够更容易地从宿主传递到宿主。 因此,人类疫情在城市中尤为严重。 事实上,自人类开始生活在城市以来的大部分时间里,城市人口只能通过持续的农村移民来维持。 直到制定了社区卫生、免疫接种和其他公共卫生措施,城市才避免了疫情导致的人口周期性急剧下降。 始于十四世纪的欧洲 “黑死病” 疫情反复流行,导致人口急剧下降。 在短短三年内(1348—1350),欧洲至少有四分之一的人口死于这种疾病(可能是鼠疫)。
同样,食草动物可以更容易地在人口密集的单个植物之间传播。 这就是为什么脱衣种植(参见可持续农业)有助于控制害虫的原因。 食草动物或植物病原体可能会感染一排植物,但不太可能传播到该物种中更远的一排。
虽然不同物种之间发生种间竞争,但当同一物种的成员使用相同的资源相互伤害时,就会发生种内竞争。 例如,1980 年夏天,新英格兰南部的大部分地区遭到吉普赛蛾的侵扰(图\(\PageIndex{g}\))。 随着夏天的过去,幼虫(毛毛虫)化脓化,孵化的成虫交配,雌性在该地区的几乎每棵树上产下大量卵(每个团块含有数百个卵)。 1981 年 5 月初,从这些卵中孵出的幼毛虫开始喂食和腐烂。

结果非常引人注目:在72小时内,一棵50英尺的山毛榉树或一棵25英尺的白松树将完全脱叶。 大片森林开始呈现冬季外观,树枝上有裸露的骨架。 实际上,侵扰非常严重,以至于许多树木在毛毛虫完成幼虫发育之前就已经完全落叶了。 结果:动物大量死亡;很少有动物成功完成变态。 那么,这里有一个生动的例子,说明一个物种的成员之间对有限资源(在本例中为食物)的竞争是如何导致种群急剧下降的。 效果显然取决于密度。 去年夏天较低的种群密度使大多数动物得以完成其生命周期。
与密度无关的调节
与@@ 密度无关的因素,通常是自然界中的物理或化学因素(非生物学),无论人口密度如何,都会影响人口的死亡率,包括天气(图\(\PageIndex{h}\))、自然灾害(地震、火山、火灾等)和污染。 无论该区域碰巧有多少鹿,一只鹿都可能在森林大火中被杀死。 无论人口密度高还是低,它的存活机会都是一样的。 寒冷的冬季天气也是如此。

在现实生活中,人口调节非常复杂,密度依赖因素和独立因素可能会相互作用。 由于某些环境因素而以与密度无关的方式减少的密集人口将能够以不同于稀疏人口的方式恢复。 例如,如果还有更多的鹿需要繁殖,受严冬影响的鹿群将更快地恢复。


