7.3: 问题解决
- Page ID
- 203801
人们每天都面临问题——通常,一天中有多个问题。 有时候这些问题很简单:例如,要将披萨面团的配方加倍,只需要将食谱中的每种成分加倍。 但是,有时我们遇到的问题更为复杂。 例如,假设你有工作截止日期,你必须在工作日结束前将报告的打印副本邮寄给你的主管。 该报告具有时间敏感性,必须在一夜之间发送。 你昨晚完成了报告,但你的打印机今天无法正常工作。 你应该怎么做? 首先,你需要确定问题,然后应用解决问题的策略。
问题解决策略
当你遇到问题时,无论是复杂的数学问题还是打印机损坏,你是如何解决这个问题的? 在找到问题的解决方案之前,必须首先清楚地确定问题。 之后,可以应用许多问题解决策略中的一种,希望能找到解决方案。
解决问题的策略是用于寻找解决方案的行动计划。 不同的战略有不同的相关行动计划(表7.2)。 例如,一个众所周知的策略是反复试验。 古老的格言 “如果一开始你没有成功,那就试试,再试一次” 描述了反复试验。 就打印机损坏而言,你可以尝试检查墨水量,如果这不起作用,你可以检查以确保纸盒没有卡住。 或者打印机实际上并未连接到您的笔记本电脑。 使用反复试验时,你会继续尝试不同的解决方案,直到问题得到解决。 尽管反复试验通常不是最省时的策略之一,但它是一种常用的策略。
| 问题解决策略 | ||
|---|---|---|
| 方法 | 描述 | 示例 |
| 反复试验 | 继续尝试不同的解决方案,直到问题得到解决 | 重启手机、关闭 WiFi、关闭蓝牙以确定手机出现故障的原因 |
| 算法 | 分步解决问题的公式 | 在计算机上安装新软件的说明手册 |
| 启发式 | 一般问题解决框架 | 向后工作;将任务分成几个步骤 |
另一种策略是算法。 算法是一种解决问题的公式,它为您提供用于实现预期结果的分步说明(Kahneman,2011 年)。 你可以将算法看作是包含非常详细的指令的配方,每次执行时都会产生相同的结果。 算法在我们的日常生活中经常使用,尤其是在计算机科学中。 当你在互联网上进行搜索时,谷歌等搜索引擎会使用算法来决定哪些条目将首先出现在你的结果列表中。 Facebook还使用算法来决定在你的新闻源上显示哪些帖子。 你能确定使用算法的其他情况吗?
启发式方法是另一种解决问题的策略。 虽然必须严格遵循算法才能得出正确的结果,但启发式方法是一种通用的问题解决框架(Tversky & Kahneman,1974 年)。 你可以把这些看作是用来解决问题的心理捷径。 “经验法则” 就是启发式方法的一个例子。 这样的规则可以在人们做出决定时节省时间和精力,但是尽管它具有节省时间的特点,但它并不总是做出理性决策的最佳方法。 不同类型的启发式方法用于不同类型的情况,但是当满足五个条件之一时,就会产生使用启发式方法的冲动(Pratkanis,1989 年):
向后工作是一种有用的启发式方法,在这种方法中,你可以通过关注最终结果来开始解决问题。 举这个例子:你住在华盛顿特区,受邀参加周六下午 4 点在费城举行的婚礼。 知道95号州际公路往往会在一周中的任何一天回转,因此您需要计划路线并相应地安排出发时间。 如果你想在下午 3:30 之前参加婚礼服务,并且在没有交通的情况下到达费城需要 2.5 个小时,那么你应该什么时候离开家? 你使用向后工作的启发式方法来定期计划当天的事件,可能甚至没有考虑过。
另一个有用的启发式方法是通过将大型目标或任务分解成一系列较小的步骤来完成该目标或任务。 学生经常使用这种常用的方法来完成大型研究项目或学校的长篇论文。 例如,学生通常集思广益,撰写论文或主要话题,研究所选主题,将他们的信息整理成大纲,撰写草稿,修改和编辑草稿,制定最终草稿,整理参考文献清单,并在上交项目之前校对他们的作品。 当将大型任务分解为一系列小步骤时,它就会变得不那么艰巨。
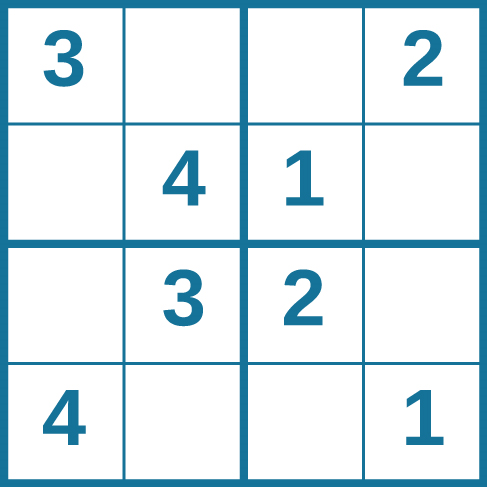
通过练习,解决问题的能力可以提高。 许多人每天通过拼图和其他心理练习来挑战自己,以提高他们解决问题的能力。 数独谜题每天都会出现在大多数报纸上。 通常,数独拼图是一个 9×9 的网格。 下面的简单数独(图 7.7)是一个 4×4 的网格。 要解开拼图,请在空框中填写一个数字:1、2、3 或 4。 以下是规则:每个粗体框、每行和每列中的数字总数必须为 10;但是,每个数字只能在粗体框、行和列中出现一次。 在解开这个难题时自己抽出时间,和同学比较一下你的时间。
解决问题的陷阱
但是,并非所有问题都能成功解决。 哪些挑战阻止我们成功解决问题? 阿尔伯特·爱因斯坦曾经说过:“疯狂正在一遍又一遍地做同样的事情,并期望得到不同的结果。” 想象一下,一个人在一个有四个门口的房间里。 过去一直开着的一扇门现在被锁上了。 这个人习惯于通过那个特定的门口离开房间,尽管其他三个门口已经打开,但一直试图通过同一个门口出来。 这个人被卡住了,但她只需要去另一个门口,而不是试图从上锁的门口出来。 思维模式是指你坚持以过去行之有效但现在显然行不通的方式处理问题。
功能固定性是一种心理习惯,在这种状态下,除了物体设计的目的之外,你无法感知到物体被用于其他用途。 邓克(1945)对功能固定性进行了基础研究。 他创建了一个实验,给参与者一支蜡烛、一本火柴书和一盒图钉。 他们被指示使用这些物品将蜡烛固定在墙上,这样蜡烛就不会滴到下面的桌子上。 参与者必须使用功能修复来解决问题(图 7.10)。 在阿波罗13号登月任务期间,Mission Control的NASA工程师不得不克服功能上的固定性,以挽救航天器上宇航员的生命。 航天器模块的爆炸损坏了多个系统。 由于二氧化碳过滤器出现问题,宇航员有因二氧化碳含量上升而中毒的危险。 工程师们找到了一种方法,让宇航员使用备用的塑料袋、胶带和空气软管来制造临时空气过滤器,从而挽救了宇航员的生命。
研究人员已经调查了功能固定性是否受到培养的影响。 在一项实验中,厄瓜多尔舒尔组的个人被要求将物体用于该物体原本打算以外的目的。 例如,向参与者讲述了一个关于熊和一只兔子被河流隔开的故事,并要求他们在各种物体中进行选择,包括勺子、杯子、橡皮擦等,以帮助动物。 汤匙是唯一一个足以穿越虚构河流的物体,但是如果汤匙的呈现方式能反映其正常使用情况,则参与者需要更长的时间才能选择汤匙来解决问题。 (德国和巴雷特,2005)。 研究人员想知道接触高度专业化的工具(例如工业化国家的个人)是否会影响他们超越功能固定性的能力。 已确定在工业化文化和非工业化文化中都存在功能固定性(German & Barrett,2005)。
为了做出正确的决定,我们运用我们的知识和推理。 通常,这种知识和推理是合理而扎实的。 但是,有时候,我们会被偏见或其他人操纵局势所左右。 例如,假设你和三个朋友想租房,总目标预算为1600美元。 房地产经纪人只给你看1600美元的非常破旧的房子,然后给你看一栋价格为2,000美元的非常漂亮的房子。 你能要求每个人多付租金才能买到 2,000 美元的房子吗? 房地产经纪人为什么要给你看破旧的房子和漂亮的房子? 房地产经纪人可能正在挑战你的锚定偏见。 当你在做出决定或解决问题时专注于一条信息时,就会出现锚定偏见。 在这种情况下,你过于关注自己愿意花多少钱,以至于你可能不知道在这个价位上有哪些类型的房屋可供选择。
确认偏见是倾向于关注证实你现有信念的信息。 例如,如果你认为你的教授不太友善,你会注意到教授表现出的所有粗鲁行为实例,却忽略了他每天参与的无数愉快互动。 Hindsight 的偏见让你相信,你刚刚经历的事件是可以预见的,尽管事实并非如此。换句话说,你一直都知道事情会像以前那样。 代表性偏见描述了一种错误的思维方式,在这种思维方式中,你无意中刻板印象了某人或某物;例如,你可能会假设你的教授把空闲时间花在读书和进行智力对话上,因为他们花时间玩游戏的想法排球或参观游乐园不符合你对教授的刻板印象。
最后,可用性启发式方法是一种启发式方法,您可以根据示例、信息或近期经验做出决定,尽管它可能不是为您的决策提供依据的最佳示例。 偏见倾向于 “保留已经确立的东西,以维持我们先前存在的知识、信念、态度和假设”(Aronson,1995;Kahneman,2011)。 表 7.3 总结了这些偏见。
| 决策偏差摘要 | |
|---|---|
| 偏见 | 描述 |
| 锚固 | 在做出决策或解决问题时,倾向于将注意力集中在一条特定的信息上 |
| 确认 | 专注于证实现有信念的信息 |
| Hindsight | 相信刚刚经历的事件是可以预见的 |
| 代表 | 对某人或某物的无意刻板印象 |
| 可用性 | 决定要么基于现有的先例,要么是基于可能错误的例子 |
观看这段由教师制作的关于认知偏见的音乐视频,了解更多信息。