11.6: 标准模型

Last updated
Save as PDF

Page ID: 201932

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

用四种基本力和交换粒子来描述标准模型
绘制费曼图，进行简单的粒子相互作用
使用海森堡的不确定性原理来确定标准模型描述的力范围
解释大统一理论背后的基本原理

任何科学家的主要智力活动都是科学模型的开发和修改。一位粒子物理学家试图开发粒子相互作用的模型。这项工作直接建立在十七、十八和十九世纪在重力和电磁学方面的工作基础上。物理学的最终目标是建立统一的 “万物理论”，用一个优雅的方程和一张图片来描述所有粒子的相互作用。这个方程本身可能很复杂，但许多科学家怀疑方程背后的想法会让我们惊呼：“我们怎么会错过它？太明显了！”

在本节中，我们将介绍标准模型，这是目前最好的粒子相互作用模型。我们从电磁、弱核和强力的角度详细描述了标准模型。在本节的最后，我们将回顾粒子物理学中的统一理论。

标准模型简介

粒子相互作用的标准模型包含两个概念：电弱理论和量子色动力学（QCD）（作用于颜色电荷之间的力）。 Electroweak 理论统一了量子电动力学（QED）理论（现代等同于经典电磁学）和弱核相互作用理论。标准模型结合了相对论和量子力学。

在标准模型中，粒子相互作用是通过玻色子（“力载体”）的交换发生的。例如，静电力是通过发送和接收无质量光子在两个带正电荷的粒子之间传递的。这可能发生在理论上的无限范围内。这些相互作用的结果是库仑排斥（或吸引）。同样，夸克通过交换无质量胶子结合在一起。轻子通过交换大量 W 和 Z 玻色子散射出其他轻子（或分解成更轻的粒子）。表中给出了标准模型所描述的力的摘要\(\PageIndex{1}\)。为了完整起见，在本表中添加了由无质量引力的交换介导的引力，但不是标准模型的一部分。

表\(\PageIndex{1}\)：四种力量和标准模型
原力	相对强度	交换粒子（玻色子）	作用的粒子	范围
强	1	Gluon	夸克	\(10^{-15}m\)
电磁	1/137	光子	带电粒子	\(\infty\)
弱	\(10^{-10}\)	\(W^+, \, W^-, \, Z\)玻色子	夸克、轻子、中微子	\(10^{-18}m\)
引力	\(10^{-38}\)	引力子	所有粒子	\(\infty\)

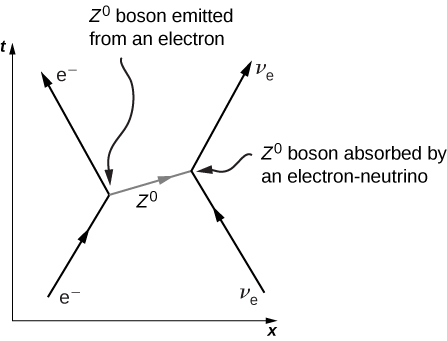
标准模型可以用方程和图表来表示。这些方程很复杂，通常在更高级的现代物理学课程中介绍。但是，可以使用费曼图来捕捉标准模型的本质。费曼图是由美国物理学家理查德· 费曼（Richard Feynman）（1918—1988）发明的，是一种描述粒子如何运动和相互作用的时空图。不同的符号用于不同的粒子。一维中的粒子相互作用显示为时间位置图（不是位置-时间图）。举个例子，以电子和电子中微子的散射为例（图\(\PageIndex{1}\)）。电子向 x 的正值（向右）移动，并与向左移动的电子中微子碰撞。电子交换 Z 玻色子（电荷为零）。电子向左散射，中微子向右散射。这种交换不是即时的。 Z 玻色子在短时间内从一个粒子传播到另一个粒子。据说电子和中微子的相互作用是通过弱核力量发生的。这种力无法用经典的电磁学来解释，因为中微子的电荷为零。本节稍后将再次讨论弱核力量。

图是 t 与 x 的对比图。标有 e 减号的箭头向上和向右移动，与另一个标有 e 减去的向上和向左箭头的底部相遇。交界处被标记为电子发射的 z0 玻色子。右边是一个向上和向左移动的箭头。尖端与另一个向上和向右移动的箭头的底部相遇。两者都被标记为 v 下标 e，交界处标记为 z0 玻色子被电子中微子吸收。图中的两个交汇点由标有 z0 的射线连接。这指向右边，略微向上。 — 图\(\PageIndex{1}\)：在这张费曼图中，虚拟的交换在**电子和中微子之间\(**Z^0\)**携带微弱的核力。**

电磁力

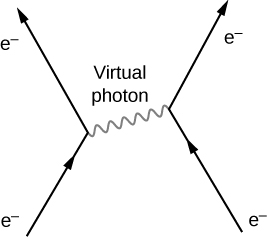
根据QED，电磁力是通过光子交换在带电粒子之间传输的。该理论基于三个基本过程：电子从一个地方传播到另一个地方，发射或吸收光子，然后再次从一个地方传播到另一个地方。当两个电子相互作用时，一个电子发射光子，另一个电子接收光子（图\(\PageIndex{2}\)）。光子将能量和动量从一个电子传递到另一个电子。在这种情况下，最终结果是排斥力量。交换的光子是虚拟的。虚拟粒子是存在时间太短而无法观测的粒子。由于光子传输时间\(\Delta t\)非常短，海森堡的不确定性原理指出，光子能量中的不确定性可能非常大。\(\Delta E\)

图中显示了四个标有 e 减号的箭头。一个向上和向右移动，然后与另一个向上和向左移动的箭头的底部相遇。右边是一个向上和向左移动的箭头。尖端与另一个向上和向右移动的箭头的底部相遇。图表上的两个交汇点由一条标为虚拟光子的波浪线相连。这指向右边，略微向上。 — 图\(\PageIndex{2}\)：费曼示意图，描绘了两个电子通过光子交换相互作用。

要估计电磁相互作用的范围，假设能量的不确定性与光子本身的能量相当，书面写成

\[\Delta E \approx E. \nonumber \]

海森堡不确定性原则指出

\[\Delta E \approx \frac{h}{\Delta t}. \nonumber \]

结合这些方程，我们有

\[\Delta t \approx \frac{h}{E}. \nonumber \]

光子的能量由给出\(E = hf\)，所以

\[\Delta t \approx \frac{h}{hf} \approx \frac{1}{f} = \frac{\lambda}{c}. \nonumber \]

因此，光子在这段时间内可以移动的距离 d 是

\[d = c\Delta t \approx c\left(\frac{\lambda}{c}\right) = \lambda. \nonumber \]

虚拟光子的能量可以任意小，因此其波长可以任意大，原则上甚至是无限大。因此，电磁力是一种远程力。

弱核力量

弱核力量是放射性衰变的原因。弱核力的射程非常短（只有大约\(10^{-18}\) m），与标准模型中的其他力一样，弱力可以用粒子交换来描述。（没有像库仑力这样的简单函数可以描述这些相互作用。）交换的粒子是三个玻色子之一：\(W^+\)、\(W^-\)和\(Z^0\)。标准模型预测了这些自旋1粒子的存在，还预测了它们的比重。结合之前的实验，预计带电 W 玻色子的质量为\(81 \, GeV/c^2\)，而带电 W 玻色子的质量预计\(Z^0\)为\(90 \, GeV/c^2\)。欧洲核子研究组织的一项实验在20世纪80年代发现了正是这些质量的粒子，这对于该模型来说是一次令人印象深刻的胜利。

弱核力最常与不稳定粒子的散射和衰变为轻粒子有关。例如，中子通过微弱的核力量衰变为质子。这个反应是写的

\[n \rightarrow p + e^- + \nu_e, \nonumber \]

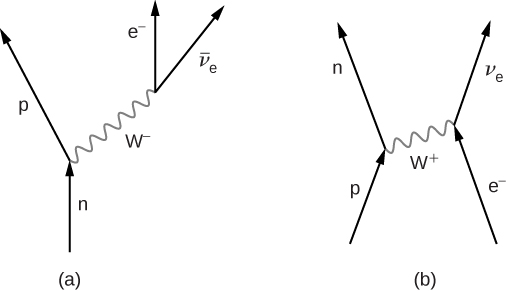
其中 n 是中子，p 是质子，\(e^-\)是电子，\(\nu_e\)是几乎没有质量的电子中微子。这个过程称为β衰变，在许多物理过程中都很重要。图中给出了费曼β衰变图\(\PageIndex{3a}\). 中子发出 a\(W^-\) 并变成质子，然后\(W^-\)产生电子和反中微子。这个过程类似于散射事件

\[e^- p \rightarrow n + \nu_e, \nonumber \]

在这个过程中，质子发出 a\(W^+\) 并转化为中子（图\(\PageIndex{3b}\)）。 \(W^+\)然后与电子结合，形成中微子。练习中还考虑了其他电弱相互作用。

图 a 显示了四个箭头。一个标有 n 的箭头指向上方，其尖端与另一个向上和向左移动的箭头的底部相交，标有 p。右边是一个标有 e 减号的箭头，指向上方。它的底座与另一个向上和向右移动的箭头的底部相连。它被标记为 v bar 下标 e。图中的两个交汇点由一条标为 W 减去的波浪线相连。这指向上和向右。图 b 显示了四个箭头。一个标有 p 的箭头指向上和向右。它的尖端与另一个向上和向左移动的箭头的底部相遇，标有 n。右边是一个标有 e 减号的箭头，指向上和向左。它的尖端与另一个向上和向右移动的箭头的底部相遇。它被标记为 v 下标 e。图中的两个交汇点由一条标为 W plus 的波浪线相连。这指向上和向右。 — 图\(\PageIndex{3}\)：费曼粒子通过交换 W 玻色子相互作用的示意图：(a) β 衰变；(b) 质子转化为中子。

弱核力量的范围可以用与之前类似的论点来估计。假设能量的不确定性与交换粒子的能量相当\((E \approx mc^2)\)，我们有

\[\Delta t \approx \frac{h}{mc^2}. \nonumber \]

因此，交换粒子可以传播的最大距离 d（假设它以接近 c 的速度移动）为

\[d \approx c\Delta t = \frac{h}{mc}. \nonumber \]

对于其中一个带电矢量玻色子\(mc^2 \approx 80 BeV = 1.28 \times 10^{-8} J\)，我们得到\(mc = 4.27 \times 10^{-17} \, J \cdot s/m\)。因此，该玻色子介导的力范围为

强大的核力量

强核相互作用描述夸克之间的相互作用。 QCD 描述了这些互动的细节。根据这个理论，夸克通过发送和接收胶子结合在一起。正如夸克携带电荷 [决定夸克之间电磁相互作用的强度] 一样，夸克也携带 “彩色电荷”（红色、蓝色或绿色），决定强核相互作用的强度。\((+2/3)e\)\((-1/3)e\) 如前所述，夸克以中性色（或 “白色”）组合（例如红蓝绿色和红反红）组合在一起。

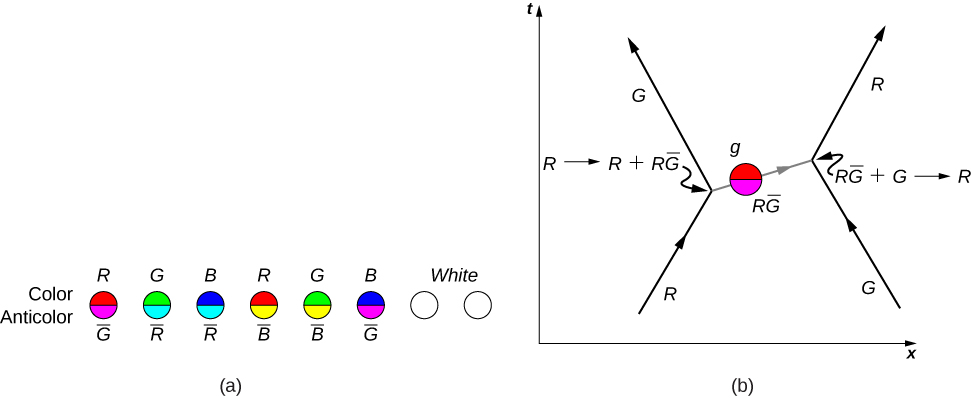
有趣的是，胶子本身带有颜色电荷。存在八个已知的胶子：六个带有彩色和反色的胶子，两个是中性色的（图\(\PageIndex{4a}\)）。为了说明夸克通过交换带电胶子之间的相互作用，请考虑图中的费曼图\(\PageIndex{4b}\)。随着时间的推移，一个红色的向下夸克向右移动，一个绿色的奇怪夸克向左移动。（它们出现在图表的下边缘。）向上的夸克与奇怪的夸克交换红色的反绿胶子。（反色显示为次要颜色。例如，antired 用青色表示，因为青色与红色混合形成白光。）根据QCD的说法，该过程中的所有相互作用（以顶点标识）都必须是色彩中性的。因此，向下的夸克从红色变为绿色，奇怪的夸克从绿色变为红色。

图 a 显示了连续 8 个圆圈。最后两个圆圈是白色的。前六个圆圈的上半部分和下半部分颜色不同。上半部分标记为颜色，下半部分标记为反色。每个圆的上半部分从左到右如下所示：第一：红色标记 R，洋红色标记 G bar；第二：绿色标记 G，青色标记 R bar；第三：蓝色标记 B，青色标记 R bar；第四：红色标记 R，黄色标记 B bar；第五：绿色标记 G，黄色标记 B bar，第六：蓝色标记 B 和洋红色标记 G 条。图 b 是 t 与 x 的对比图。向上和向右移动的箭头被标记为 R。它的尖端与箭头 G 的底部相交，箭头指向上和向左。交汇点的标签从 R 到 R 再加上 R G 条。右边是指向上和向左的箭头 G。它的尖端与箭头 R 的底部交汇处。交汇点从 RG bar 加 G 到 R 进行标记。两个交汇点通过指向右侧的箭头相连。箭头上有一个标有 RG 条的圆圈。 — 图\(\PageIndex{4}\)：（a）八种胶子携带强大的核力。白色胶子是彩色-反色对的混合物。 (b) 两个夸克之间通过胶子交换相互作用。

正如这个例子所示，原子核中夸克之间的相互作用可能非常复杂。该图\(\PageIndex{5}\)显示了质子和中子之间的相互作用。请注意，在相互作用过程中，质子会转化为中子，而中子会转化为质子。交换中存在 quark-antiquark 对表明，核子之间的键合可以建模为介子的交换。

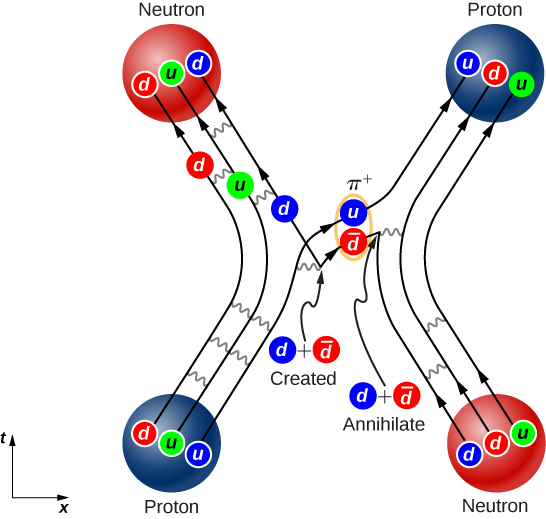
图的左上角是一个标有中子的圆圈。里面有三个标有 d、u、d 的小圆圈。右上角是一个标有质子的圆圈。里面有三个标有 u、d、u 的圆圈。右下角是一个标有 neutron 的圆圈。里面有三个标有 d、d、u 的圆圈。左下角是一个标有质子的圆圈。里面有三个标有 d、u、u 的圆圈。左下角质子中 d 和 u 的线与左上角中子的 d 和 u 相连。来自右下角中子的 d 和 u 的线与右上角质子中的线相连。从左下角质子 u 开始的一条线与右上角质子中的 u 相连。在这条连接线的中间，u 与另一个标有 d bar 的圆配对。这对被标记为 pi plus。指向左侧标有 d bar 的圆圈是一个箭头，其底部标有 d 加上 d bar 创建的。箭头底部的一条线与左上角中子的 d 相连。标有 d bar 的圆的右边是一条线，其端点标记为 d plus d bar annihilate。一条线将右下角中子中的d连接到它。所有连接线之间都显示了波浪线。 — 图\(\PageIndex{5}\)：费曼图，描述了质子和中子之间的强核相互作用。

实际上，QCD 的预测很难生成。这种困难源于力量的固有力量以及无法忽视方程中的术语。因此，QCD 计算通常是在超级计算机的帮助下进行的。胶子的存在得到了电子-核子散射实验的支持。这些散射事件所暗示的估计夸克力矩比我们在没有胶子的情况下预期的要小得多，因为胶子会带走每次碰撞的部分动量。

统一理论

物理学家早就知道，粒子之间相互作用的强度取决于相互作用的距离。例如，两个带正电荷的粒子在短距离内比在远距离上承受的排斥力更大。在散射实验中，相互作用的强度取决于相互作用粒子的能量，因为较大的能量意味着更紧密和更强的相互作用。

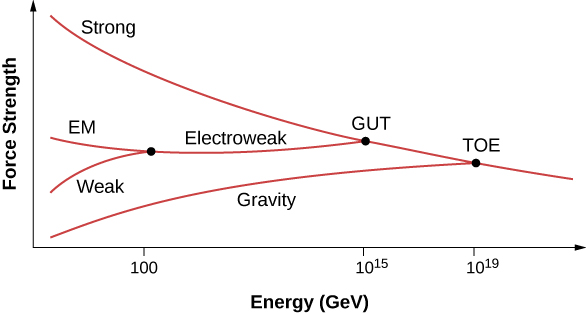
GeV 中力强度与能量的对比图。一条标有向下和向右强斜率的曲线。曲线上的 x 值为 10 到 19 的幂的点被标记为 TOE。一条标有重力的曲线从这里向外分支，向下和向左移动。强曲线上的 x 值为 10 到 15 的次方，被标记为 GUT。一条向左延伸的曲线从这里伸出来。它被称为 Electroweak。这在 x 值为 100 的点处分为两个。向左移动的分支被标记为 EM，向下和向左移动的树枝被标记为弱。 — 图\(\PageIndex{6}\)：高能量的力量大统一。

粒子物理学家现在怀疑，所有粒子相互作用（四种力）的强度以高能量融合，这些能量下粒子相互作用的细节可以用单一力来描述（图\(\PageIndex{6}\)）。统一的理论描述了这些相互作用是什么样的，并解释了为什么这种描述在低能量尺度上会崩溃。宏伟的统一理论是一种试图用一种力来描述强和电弱相互作用的理论。万物理论（TOE）使统一概念更进一步。 TOE 将所有四种基本力（包括重力）合并为一个理论。