11.7: 宇宙大爆炸
- Page ID
- 201939
在本节结束时,您将能够:
- 用哈勃图和宇宙学红移来解释宇宙的扩张
- 描述宇宙学膨胀和膨胀气球之间的类比
- 使用哈勃定律预测遥远星系的测得速度
我们一直在讨论基本粒子,这是我们可以研究的最小东西。 现在我们要研究一下我们对宇宙的了解,这是我们能研究的最大的东西。 这两个主题之间的联系是高能量:对粒子相互作用的研究需要非常高的能量,而我们所知道的最高能量存在于宇宙的早期演变。 一些物理学家认为,我们在上一节中描述的统一力理论实际上可能在宇宙最早的时刻就控制了宇宙的行为。
哈勃定律
1929年,埃德温·哈勃发表了现代天文学中最重要的发现之一。 哈勃发现了这一点
- 星系似乎正在远离地球
- 衰退速度 (\(v\)) 与银河系与地球的距离 (\(d\)) 成正比。
两\(v\)者都\(d\)可以使用恒星光谱来确定。 图中给出了最适合示例说明性数据的方法\(\PageIndex{1}\)。 (哈勃最初的情节有相当大的分散,但总体趋势仍然很明显。)
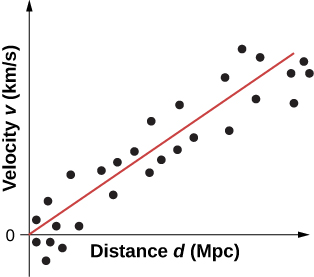
数据中的趋势表明了简单的比例关系:
\[v = H_0d, \nonumber \]
其中\(H_0 = 70 \, km /s /Mpc\)被称为哈勃常数。 (注意:1 Mpc 等于 1 兆帕秒或一百万秒差距,其中 1 秒差距为 3.26 光年。) 这种关系被称为哈勃定律,它指出,距离我们每隔一兆帕秒,遥远的恒星和星系就会以70 km/s的速度从我们身边消失。 哈勃常数对应于图中直线的斜率\(\PageIndex{1}\)。 哈勃的常数有点用词不当,因为它会随着时间的推移而变化。 这里给出的值只是它今天的价值。
观看此视频,详细了解哈勃常数的历史。
宇宙膨胀的速度,这个值被称为哈勃常数,在过去的80年中一直备受争议。 现在,卡内基天文台的主任温迪·弗里德曼将领导一个团队,该团队将使用美国宇航局的天基斯皮策望远镜通过新的卡内基哈勃计划将这一值的不确定性降低到仅3%。
哈勃定律描述了除最近的星系之外的所有星系的平均行为。 例如,一个距离 100 Mpc 的星系(由其大小和亮度决定)的移动速度通常为
\[v = \left( \left( 70 \frac{km}{s}\right)/Mpc \right) (100 \, Mpc) = 7000 \, km/s. \nonumber \]
由于与邻近星系的相互作用,该速度可能会有所不同。 相反,如果发现一个星系根据其红移以 100,000 km/s 的速度远离我们,则它处于一定距离
\[d = v/H_0 = (10,000 \, km/s)/ \left( \left( 70 \frac{km}{s}\right) /Mpc \right) = 143 \, Mpc. \nonumber \]
最后一次计算是近似值,因为它假设扩张率与50亿年前的扩张率与现在相同。
宇宙大爆炸模型
研究宇宙起源、演变和最终命运(宇宙学)的科学家认为,宇宙始于大约137亿年前的一次爆炸,称为宇宙大爆炸。 这次爆炸不是像烟花一样的粒子在太空中爆炸,而是太空本身的快速扩张。 外向恒星和星系的距离和速度使我们能够估计宇宙中所有物质何时在一起——在时间开始时。
科学家经常使用充气气球模型来解释宇宙大爆炸的扩张(图\(\PageIndex{2}\))。 气球表面标记的点代表星系,气球皮肤代表四维时空。 当气球充气时,每个点 “看见” 其他圆点正在移开。 该模型得出了两个见解。 首先,宇宙中的所有观察者都会观察到膨胀,无论他们身在何处。 “扩张中心” 不存在,因此地球不在扩张的 “特权” 中心。
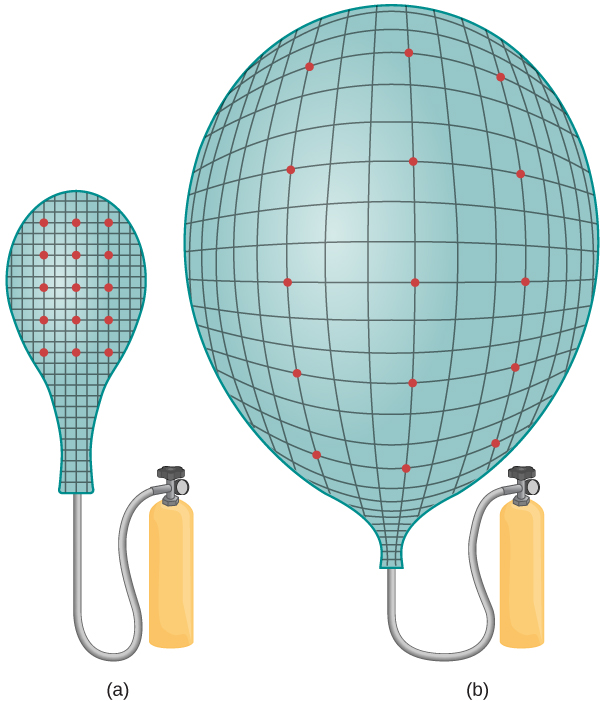
其次,如前所述,宇宙大爆炸的扩张是由于空间的扩张,而不是普通(静态)三维空间中星系分离的增加。 这种宇宙学的扩张影响着所有事物:尘埃、恒星、行星甚至光。 因此,遥远星系发出的光 (\(\lambda\)) 的波长被 “拉伸” 了。 这使得光线对观察者来说显得 “更红”(能量更低),这种现象被称为宇宙学红移。 只有距离超过5000万光年的星系才能测量宇宙学红移。
观察到星系有红移:
\[z = \frac{\lambda_{obs} - \lambda_{emit}}{\lambda_{emit}} = 4.5. \nonumber \]
该值表示星系的移动速度接近光速。 使用相对论红移公式(在相对论中给出)确定:
- 银河系相对于地球的退缩速度有多快?
- 银河系有多远?
策略
我们需要使用相对论的多普勒公式来确定从红移开始的速度,然后使用哈勃定律来找出与速度的距离。
解决方案
- 根据相对论的红移公式:\[z = \sqrt{\frac{1 + \beta}{1 - \beta}} - 1, \nonumber \]在哪里\(\beta = v/c\)。 将值替换为 z 并求解\(\beta\),我们得到\(\beta = 0.93\)。 该值表示星系的速度为\(2.8 \times 10^8 \, m/s\)。
- 根据哈勃定律,如果我们知道银河系的衰退速度,我们就能找到到银河系的距离:\[d = \frac{v}{H_0} = \frac{2.8 \times 10^8 \, m/s}{73.8 \times 10^3 \, m/s \, per \, Mpc} = 3.8 \times 10^3 \, Mpc. \nonumber \]
意义
遥远的星系似乎非常迅速地离开地球。 来自这些星系的星光的红移可以用来确定衰退的精确速度,在本例中超过\(90%\)光速。 这种运动不是由于星系在太空中的运动,而是由于空间本身的扩张。
远离我们的星系的光线被 “红移”。 向我们移动的星系的光会怎样?
- 回答
-
blueshifted
观看此视频,了解有关宇宙学扩张的更多信息。
不断膨胀的宇宙。
宇宙的结构和动力学
在大尺度上,人们认为宇宙既是各向同性又是同质的。 宇宙之所以被认为是各向同性的,是因为它在各个方向上看起来都是一样的,而同质是因为它在所有地方看起来都是一样的。 据说各向同性且均匀的宇宙是光滑的。 20世纪80年代和1900年代进行的自动板块测量银河调查支持了宇宙光滑的假设(图\(\PageIndex{3}\))。 但是,甚至在收集这些数据之前,理论家就使用了平滑宇宙的假设来简化宇宙膨胀模型。 这种平滑宇宙的假设有时被称为宇宙学原理。

这个不断膨胀而平滑的宇宙的命运还是一个悬而未决的问题。 根据广义相对论,表征宇宙状态的一个重要方法是通过时空度量:
\[ds^2 = c^2dt^2 - a(t)^2 d\Sigma^2, \nonumber \]
其中 c 是光速,a 是比例因子(时间函数),\(d\Sigma\)是空间的长度元素。 在球坐标中\((r, \theta, \phi)\),这个长度元素可以写入
\[d\Sigma^2 = \frac{dr^2}{1 - kr^2} + r^2(d\theta^2 + sin^2 \theta d\varphi^2), \nonumber \]
其中 k 是一个以反面积为单位的常数,用于描述空间的曲率。 这个常数区分开放宇宙、封闭宇宙和平坦宇宙:
- \(k = 0\)(扁平宇宙)
- \(k > 0\)(封闭的宇宙,例如球体)
- \(k < 0\)(开放宇宙,比如双曲线)
就比例因子 a 而言,该指标还区分了静态宇宙、膨胀宇宙和收缩宇宙:
- \(a = 1\)(静态宇宙)
- \(da/dt > 0\)(不断膨胀的宇宙)
- \(da/dt < 0\)(宇宙萎缩)
比例因子 a 和曲率 k 由爱因斯坦的广义相对论确定。 如果我们将宇宙视为密度和压力 p 的星系气体,\(\rho\)并假设\(k = 0\)(一个平坦的宇宙),那么比例因子 a 的计算公式为
\[\frac{d^2a}{dt^2} = - \frac{4\pi G}{3} (\rho + 3p) a, \nonumber \]
其中 G 是通用引力常数。 (对于普通物质,我们预计数量\(\rho + 3p\)将大于零。) 如果比例因子为正\((a > 0)\),则比例因子的值 “减速”\((d^2a/dt^2 < 0)\),宇宙的膨胀会随着时间的推移而减慢。 如果分子小于零(不知何故,宇宙的压力为负),则比例因子的值 “加速”,宇宙的膨胀会随着时间的推移而加速。 根据最近的宇宙学数据,宇宙似乎正在膨胀。 许多科学家用早期宇宙的快速膨胀来解释宇宙的现状。 这种扩张被称为通货膨胀。


