11.4: 夸克斯
- Page ID
- 201946
在本节结束时,您将能够:
- 比较和对比六个已知夸克
- 使用强子的夸克成分来确定这些粒子的总电荷
- 解释夸克存在的主要证据
20 世纪 60 年代,粒子物理学家开始意识到强子 不是基本粒子,而是由称为 夸克的粒子组成的。 (“夸克” 这个名字是由物理学家 默里· 盖尔曼根据詹姆斯·乔伊斯小说《芬尼根的觉醒》中的一句话创造的。) 最初,人们认为只有三种夸克,分别是 u p (u)、d own (d) 和 奇怪 (s)。 但是,这个数字很快增加到 六个(有趣的是,与轻子的数量相同),包括 charmed(c)、bott om(b)和 顶部(t)。
所有夸克都是自旋半费密子\((s = 1/2)\),具有 分数电荷\((1/3\)或\(2/3 e)\),并且有重子数 \(B = 1/3\)。 每个夸克都有一个质量相同但电荷和重子数 相反的反夸克。 表中列出了 六夸克的名称和属性。
| 夸克 | 电荷( e 单位) | 旋转 | 重子 数 | 陌生 数 |
|---|---|---|---|---|
| 向下 (d) | - 1/3 | 1/2 | 1/3 | 0 |
| 向上 (u) | + 2/3 | 1/2 | 1/3 | 0 |
| 奇怪 | - 1/3 | 1/2 | 1/3 | - 1 |
| 吊饰 (c) | + 2/3 | 1/2 | 1/3 | 0 |
| 底部 (b) | - 1/3 | 1/2 | 1/3 | 0 |
| 上衣 (t) | + 2/3 | 1/2 | 1/3 | 0 |
夸克组合
如前所述,夸克以两 三个为一组的形式结合在一起形成强子。 重子由三个夸克形成。 表 中给出了样本重子,包括夸克含量和属性。 有趣的是,delta plus (\(\Delta^+\)) 重子是由与质子相同的三个夸克 形成的,但粒子的总自旋 为 3/2 而不是 1/2。 同样,自旋 3/2 的 \(\Delta^+\)质量是质子质量的 1.3 倍,自旋 3/2 的 delta zero (\(\Delta^0\)) 重子是中子质量的 1.3 倍 。 显然,与粒子的自旋 (或角动量)相关的能量为其质量 能量做出了贡献。 同样有趣的是,据信顶级夸克不 存在重子,因为顶级夸克衰减得太快,无法在生产中与其他夸克结合 。
| 姓名 | 符号 | 夸克 | 电荷(以 e 为单位) | 旋转 | 弥撒 \((GeV/c^2)\) |
|---|---|---|---|---|---|
| 质子 | p | uu u d | 1 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 0.938 |
| 中子 | n | ud d d | 0 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 0.940 |
| Delta plus | \(\Delta^{++}\) | uu u u u | 2 | 3/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.232 |
| 达美加号 | \(\Delta^+\) | uu u d | 1 | 3/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.232 |
| 零三角洲 | \(\Delta^0\) | ud d d | 0 | 3/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.232 |
| 增量减去 | \(\Delta^-\) | d d d | -1 | 3/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.232 |
| Lambda 零 | \(\Lambda^0\) | ud s | 0 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.116 |
| 正西格玛 | \(\Sigma^+\) | 哦你是 | 1 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.189 |
| 中性西格玛 | \(\Sigma^0\) | ud s | 0 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.192 |
| 负 xi | \(\Xi^-\) | s d s | -1 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.321 |
| 中立 xi | \(\Xi_0\) | 你是吗 | 0 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.315 |
| 欧米茄减去 | \(\Omega^-\) | s s s | -1 | 3/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 1.672 |
| 迷人的 lambda | \(\Lambda_{C+}\) | u d c | 1 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 2.281 |
| 迷人的底部 | \(\Lambda_{b0}\) | u d b | 0 | 1/2 | \ (gev/c^2)\)” style= “text-align: center;” class= “lt-phys-4557” > 5.612 |
介子由两个夸克构成,即夸克-反夸克对。 表中给出了样本 介子,包括夸克含量和属性 \(\PageIndex{3}\)。 考虑一下介子的形成(\ (\ pi^+ = u\ overline {d}\))。 根据其夸克含量, pion 的冲锋是
\[\dfrac{2}{3}e + \dfrac{1}{3}e = e. \nonumber \]
两个夸克都是 spin-half (\(s = \dfrac{1}{2}\)),因此 合成的自旋要么是 0 要么是 1。 \((\pi^+)\)介子的自旋 为 0。 同样的 quark-antiquark 组合赋予了 rho (\(\rho\)) 介子自旋 1。 这个介子的质量大约是\(\pi^+\)介 子的5.5倍。
表明 Table f\(\PageIndex{2}\) or\(\Xi^0\) 中给出的夸克成分与该重子的已知电荷、自旋和 陌生度一致。
策略
\(\Xi^0\)由两个奇怪的夸克和一个向上夸克 (s u s)组成。 我们可以将夸克的特性相加来 预测重子由此\(\Xi^0\)产生的属性。
解决方案
s 夸克的冲锋是\(-e/3\),u quark 的冲锋是 2 e /3。 因此,该组合(s u s)没有净费用,这与已知的费用一致 \(\Xi^0\)。 由于三个自旋\(-1/2\)夸克可以组合产生自旋 为 1/2 或 3/2 的粒子,因此夸克的成分与已知的自旋 (\(s = 1/2\)) 一致\(\Xi^0\)。 最后, (s u s) 组合的净奇异之处是\ ((-1) + 0 + (-1) = -2\),这也与实验一致。
意义
\(\Xi^0\)粒子的电荷、自旋和奇异度 可以根据其组成夸克的特性来确定。 重子和介子的 巨大多样性可以追溯到只有六个夸克 的特性:向上、向下、冲锋、奇怪、顶 部和底部。
介子的重子数是多少?
- 回答
-
0
颜色
夸克是服从 保利排除原则的费密子,因此得知 三个夸克可以在原子核内结合在一起可能会令人惊讶。 例如,质子 内的同一个小空间区域 怎么能存在两个向上的夸克? 解决方案是发明第三个新属性来 区分它们。 这种特性被称为 颜色,它在强核相互作用 中的作用与电荷在电磁 相互作用中的作用相同。 出于这个原因,夸克颜色有时被称为 “强电荷”。
夸克有三种颜色:红色、绿色和蓝色。 (这些 只是标签,夸克实际上不是彩色的。) 每种夸克 \((u, \, d, \, c, \, s, \, b, \, t)\)可以拥有任何其他颜色。 例如,存在三个奇怪的夸克:一个红色的奇怪夸克、一个 绿色的奇怪夸克和一个蓝色的奇怪夸克。 Antiquarks 有 防色功能。 结合在一起形成强子(重子和 介子)的夸克必须是中性、无色或 “白色”。 因此, 重子必须包含红色、蓝色和绿色夸克。 同样,介子 包含红反红、蓝反蓝或绿色反绿 夸克对。 因此,在强子中可以找到两个处于相同自旋状态 的夸克,而不会违反保利的排除原则,因为 它们的颜色不同。
夸克监禁
夸克存在的第一个有力证据来自 1970年左右在斯坦福直线 加速器中心(SLAC)和欧洲核子研究组织(CERN)进行的一系列实验。 该实验旨在探测质子的结构,就像 卢瑟福通过 \(\alpha\)粒子散射实验研究原子内部的结构一样。 电子 与能量超过 20 GeV 的质子碰撞。 在这个能量下,\ (E \ 大约 pc\),所以电子的 de Broglie 波长为
\ [\ lambda =\ dfrac {h} {p} =\ dfrac {hc} {E}\ 大约 6\ times 10^ {-17} m。\ nonumber\]
电子的波长远小于质 子的直径(大约\(10^{-15} m)\)。 因此,就像 穿越落基山脉的汽车一样,电子可以用来 探测原子核的结构。
SLAC 实验发现,一些电子以 非常大的角度偏转,这表明 质子内部的散射中心很小。 散射分布与电子 从自旋 1/2(夸克自旋)的位点散射一致。 欧洲核子研究组织的 实验使用中微子代替电子。 该 实验还发现了微小散射中心的证据。 在这 两个实验中,结果都表明 散射粒子的电荷要\(+2/3e\)么是夸克模型\(-1/3 e\),要么与夸克模型 一致。
观看此视频,了解有关夸克的更多信息。
质子和中子是由 三个夸克组成的,对吧? 错了! 探索你小时候他们应该 告诉你的粒子!
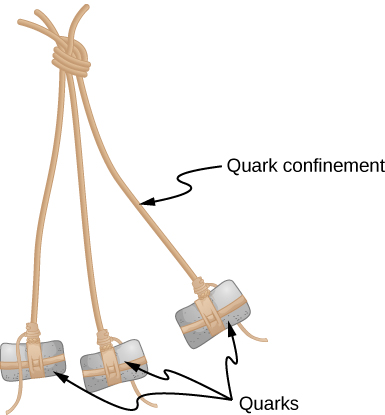
夸克模型在组织 复杂的亚原子粒子世界方面非常成功。 但有趣的是,从来没有 实验产生过孤立的夸克。 所有夸克都有 分数电荷,因此应该很容易与已知的基本粒子区 分开来,后者的电荷都是 e 的 整数倍。 为什么没有 观察到孤立的夸克? 在当前的粒子相互作用模型中,答案是用夸克限制来 表示的。 夸克限制是 指将夸克分成两三组限制在一个很小的空间 区域内。 夸克完全可以在 这个空间中自由移动,可以发送和接收胶子(强 力载体)。 但是,如果这些夸克彼此偏离得太远, 则强大的力量会将它们拉回来。 这个动作被比作 bola,一种用于狩猎的武器(图\(\PageIndex{1}\))。 石头用绳子绑在中心点上,因此任何一 块岩石都无法与其他岩石移动得太远。 bola 对应于 重子,石头对应夸克,绳子对应 于将系统固定在一起的胶子。