10.6: 裂变
- Page ID
- 202257
在本节结束时,您将能够:
- 用其产物和反应物描述核裂变过程
- 计算裂变反应产生的粒子的能量
- 解释裂变炸弹和核反应背景下的裂变概念
1934 年,恩里科·费米用中子轰击化学元素,以产生其他元素的同位素。 他认为用中子轰击铀会使铀变得不稳定并产生新的元素。 不幸的是,费米无法确定反应的产物。 几年后,奥托·哈恩(Otto Hahn)和弗里茨·斯特拉斯曼(Fritz Strassman)复制了这些实验,发现这些反应的产物是较小的原核。 由此,他们得出结论,铀核已经分裂成两个较小的原核。

原子核的分裂称为裂变。 有趣的是,U-235 裂变并不总是会产生相同的碎片。 裂变反应示例包括:
\[\ce{_0^1n + _{92}^{235}U \rightarrow _{56}^{141}Ba + _{36}^{92}Kr + 3_0^1n + Q,} \nonumber \]
\[\ce{_0^1n + _{92}^{235}U \rightarrow _{54}^{140}Xe + _{38}^{94}Sr + 2_0^1n + Q,} \nonumber \]
\[\ce{_0^1n + _{92}^{235}U \rightarrow _{50}^{132}Sn + _{42}^{101}Mo + 3_0^1n + Q,} \nonumber \]
在每种情况下,产物核的质量总和小于反应物的质量,因此铀的裂变是一个放热过程\((Q > 0)\)。 这就是使用裂变反应堆作为能量来源的想法(图\(\PageIndex{1}\))。 反应带走的能量以具有动能的粒子的形式出现。 图中给出了 U-235 裂变碎片的产量百分比\(\PageIndex{2}\)。
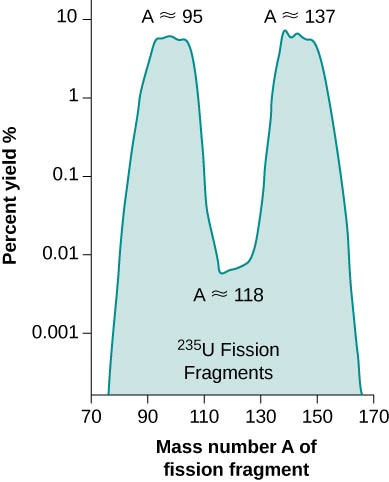
核裂变反应中的能量变化可以用每核子曲线的结合能来理解。 铀\((A = 236)\)的 BEN 值略低于其子核,后者更接近铁(Fe)峰。 这意味着核碎片中的核子比 U-235 原子核中的核子结合得更紧密。 因此,裂变反应会导致核子的平均能量下降。 这种能量被高能中子带走。
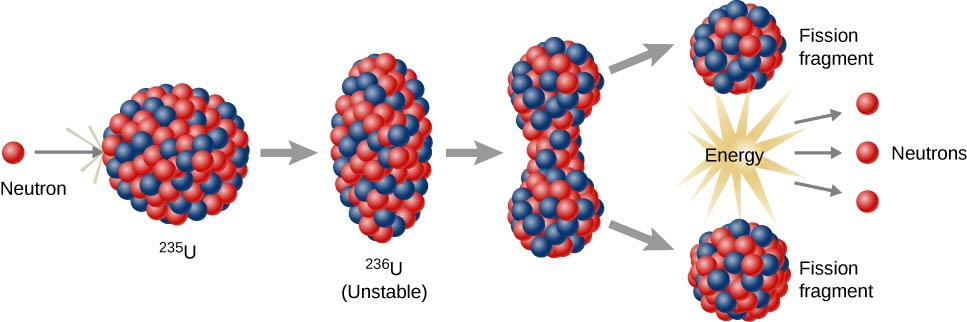
尼尔斯·玻尔和约翰·惠勒开发了液滴模型,以了解裂变过程。 根据这个模型,向原子核发射中子类似于干扰一滴水滴(图\(\PageIndex{3}\))。 这个类比之所以奏效,是因为原子核中核子之间的短程力与水滴中水分子之间的吸引力相似。 特别是,原子核表面核子之间的力会产生类似于水滴的表面张力。 发射到铀核中的中子可以使原子核进入振动状态。 如果这种振动足够剧烈,原子核就会分裂成较小的原子核,还会发射两三个单独的中子。
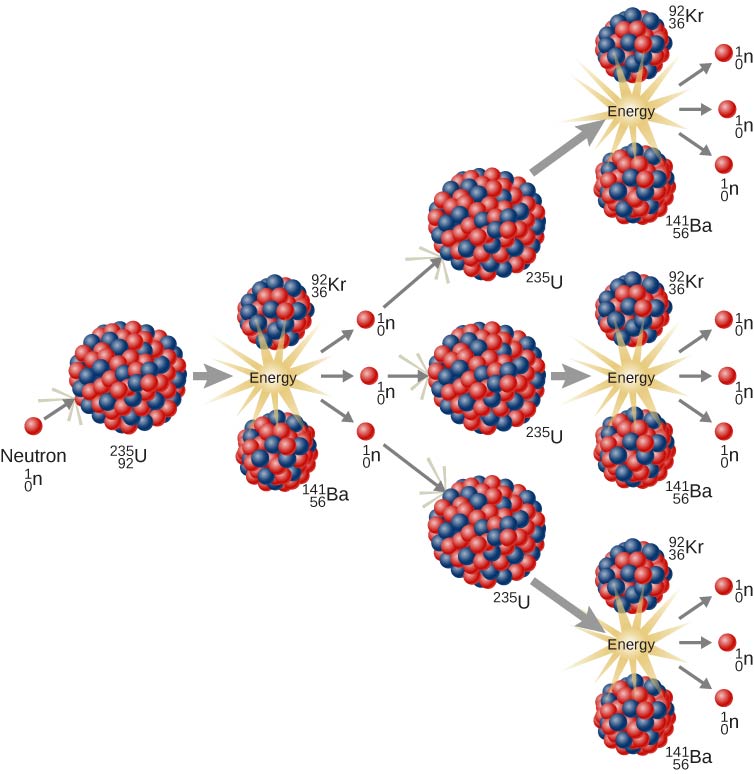
U-235 裂变可以产生核链反应。 在由许多 U-235 原子核组成的化合物中,一个 U-235 原子核衰变中的中子可以引发其他 U-235 原子核的裂变(图\(\PageIndex{4}\))。 这种连锁反应可以以受控的方式进行,例如在发电厂的核反应堆中,也可以像爆炸那样不受控制地进行。
观看核裂变模拟以启动连锁反应,或引入非放射性同位素以防止连锁反应。 控制核反应堆中的能量产生。
原子弹
铀发生连锁反应的可能性及其极大的能量释放,促使核科学家设想制造一枚炸弹—— 原子弹。 (这些发现发生在第二次世界大战之前的几年里,参与这些发现的许多欧洲物理学家来自被占领的国家。) 天然铀含有\(99.3\%\) U-238,只含有\(0.7\%\) U-235,不会产生连锁反应。 为了产生可控的、可持续的连锁反应,必须将 U-235 的百分比提高到大约\(50\%\)。 此外,铀样品必须足够大,这样典型的中子更有可能诱发裂变而不是逸出。 发生连锁反应所需的最小质量称为临界质量。 当临界质量达到连锁反应可以自我维持的程度时,这种情况被称为临界状态。 最初的设计要求两块 U-235 低于临界质量。 当子弹形式的一块子弹射入第二块时,超过临界质量并产生连锁反应。
U-235 炸弹的一个重要障碍是生产临界数量的可裂变材料。 因此,科学家研制了钚 239 炸弹,因为 Pu-239 比 U-235 更易裂变,因此需要的临界质量更小。 炸弹是以球体的形式制造的,球体的边缘有钚碎片,每块都低于临界质量。 一系列化学爆炸同时向球体中心发射了钚碎片。 当所有这些钚聚集在一起时,其组合超过了临界质量并产生了连锁反应。 U-235 和 Pu-239 炸弹都是在第二次世界大战中使用的。 是否发展和使用原子武器仍然是人类文明面临的两个最重要的问题。
计算以下罕见的自发裂变反应中释放的能量:
\[\ce{^{238}U \rightarrow ^{95}Sr + ^{140}Xe + 3n,} \nonumber \]
原子质量是\(m(^{238}U) = 238.050784 \, u\)、\(m(^{95}Sr) = 94.919388 \, u\)\(m(^{140}Xe) = 139.921610 \, u\)、和\(m(n) = 1.008665 \, u\)。
策略
与往常一样,释放的能量等于质量消灭的时间\(c^2\),因此我们必须找到母体\(^{238}U\)和裂变产物之间的质量差异。
解决方案
该产品的总质量为
\[m_{products} = 94.919388 \, u + 139.921610 \, u + 3(1.008665 \, u) \nonumber \]
\[= 237.866993 \, u. \nonumber \]
损失的质量是\(^{238}U - m_{products}\)或的质量
\[\Delta m = 238.050784 \, u - 237.8669933 \, u = 0.183791 \, u. \nonumber \]
因此,释放的能量是
\[E = (\Delta m)c^2 = (0.183791 \, u) \frac{931.5 \, MeV/c^2}{u}c^2 = 171.2 \, MeV. \nonumber \]
意义
在这个例子中出现了几个重要的事情。 能量释放量很大,但比原子核分裂成两个相等部分时要少,因为能量是由中子带走的。 但是,这种裂变反应会产生中子,不会将原子核分成两个相等的部分。 例如,给定核素的裂变并不总是会产生相同的产物。\(^{238}U\) 裂变是一种统计过程,在这个过程中,以不同的概率生产出各种产物。 大多数裂变会产生中子,尽管数量各不相同。 这是裂变的一个极其重要的方面,因为中子可以诱发更多的裂变,从而实现自我维持的连锁反应。
裂变核反应堆
1942 年 12 月 2 日,恩里科·费米在芝加哥大学校园的壁球场上建造了第一座核反应堆。 反应堆本身含有富含\(3.6\%\) U-235 的 U-238。 连锁反应产生的中子移动得太快,无法引发裂变反应。 减速的一种方法是在高压下将整个反应堆封在水浴中。 中子与水分子碰撞,速度足够慢,可以在裂变过程中使用。 减速的中子会分裂更多的 U-235 核,并发生连锁反应。 连锁反应的进行速率由插入反应器中的一系列由镉制成的 “控制” 棒控制。 镉能够吸收大量中子而不会变得不稳定。
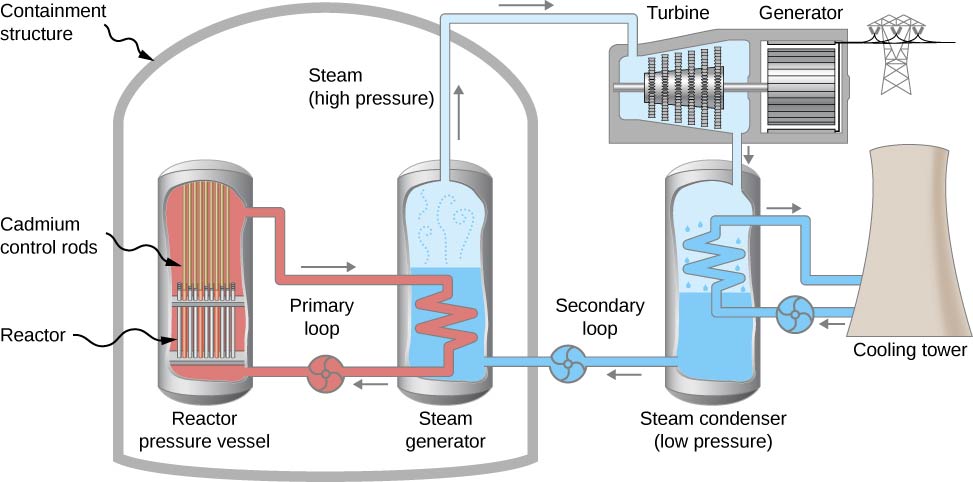
称为压水反应堆的核反应堆设计也可用于发电(图\(\PageIndex{5}\))。 压水反应堆(图左侧)旨在控制大量压水反应堆的裂变\(^{235}U\)。 在此过程中释放的能量被流经系统管道(“主回路”)的水吸收,然后产生蒸汽。 镉控制棒调整中子通量(中子通过系统的流速),从而控制反应。 如果反应堆过热而水沸腾,连锁反应就会终止,因为水被用来对中子进行热化。 (在极端情况下,此安全功能可能会不堪重负。) 然后,热的高压水在正常压力下通过管道进入蒸汽发生器中的第二个水箱。 蒸汽发生器一端产生的蒸汽填充了装有涡轮机的腔室。 这种蒸汽的压力很高。 同时,连接到涡轮机室另一侧的蒸汽冷凝器将蒸汽保持在低压下。 压力差迫使蒸汽通过腔室,从而使涡轮机转动。 反过来,涡轮机为发电机提供动力。
裂变反应堆的主要缺点是核废料。 U-235 裂变会产生半衰期较长的原核\(^{238}U\),因此必须储存。 这些产品不能倾倒到海里,也不能留在任何会污染环境的地方,例如通过土壤、空气或水。 许多科学家认为,储存核废料的最佳地点是旧盐矿的底部或稳定的山脉内。
许多人担心核反应堆可能像原子弹一样爆炸。 但是,核反应堆没有足够的 U-235 来做到这一点。 此外,核反应堆的设计使反应堆的任何机制失效都会导致镉控制棒完全落入反应堆中,从而停止裂变过程。 正如福岛和切尔诺贝利灾难所证明的那样,这样的系统可能会失效。 避免此类灾难的系统和程序是核能倡导者的重要优先事项。
如果所有电力都是由 U-235 的核裂变产生的,那么地球上已知的铀储量将在不到一个世纪的时间内耗尽。 但是,使用增殖反应堆可以大大扩大地球的可裂变材料的供应。 增殖反应堆首次使用 U-235 的裂变运行,正如刚才在压水反应堆中所描述的那样。 但是,除了产生能量外,一些源自 U-235 裂变的快中子还被 U-238 吸收,从而通过一系列反应产生 Pu-239
\[\ce{_0^1n + _{92}^{238}U \rightarrow _{92}^{239}U \rightarrow _{93}^{239}Np \rightarrow _{94}^{239}Pu.} \nonumber \]
Pu-239 本身具有很高的裂变性,因此可以用作核燃料来代替 U-235。 由于\(99.3\%\)天然存在的铀是 U-238 同位素,因此使用增殖反应堆将使我们的核燃料供应增加大约 100 倍。 增殖反应堆现已在英国、法国和俄罗斯运行。 增殖反应堆也有缺点。 首先,增殖反应堆会产生钚,如果泄漏到环境中,会造成严重的公共卫生问题。 其次,钚可以用来制造炸弹,从而大大增加了核扩散的风险。
假设平均裂变反应产生 200 兆电子伏\(^{235}U\),计算裂变\(^{235}U\)产生的能量为 1.00 kg。
策略
产生的总能量是\(^{235}U\)原子数乘以每次\(^{235}U\)裂变给定能量。 因此,我们应该找出 1.00 kg 中的\(^{235}U\)原子数。
解决方案
1.00 kg 中的\(^{235}U\)原子数是 Avogadro 的数字乘以摩尔数。 一摩尔的质量\(^{235}U\)为 235.04 g;因此,有\((1000 \, g)/(235.04 \, g/mol) = 4.25 \, mol\)。 因此,\(^{235}U\)原子的数量是
\[(4.25 \, mol)(6.02 \times 10^{23})^{235}U/mol = (2.56 \times 10^{24})^{235}U. \nonumber \]
因此,释放的总能量为
\[E = (2.56 \times 10^{24})^{235}U \left(\frac{200 \, MeV}{^{235}U} \right) \left(\frac{1.60 \times 10^{-13} \, J}{MeV} \right) = 8.21 \times 10^{13} \, J \nonumber \]
意义
这是另一种令人印象深刻的大量能源,相当于大约14,000桶原油或60万加仑汽油。 但是,它仅为一千克氘和钍混合物聚变所产生的能量的四分之一。 尽管每次裂变反应产生的能量大约是聚变反应的10倍,但每千克裂变燃料的能量要少得多,因为每千克重核素的摩尔要少得多。 裂变燃料也比聚变燃料稀缺得多,而且比\(1\%\)铀更容易使用。\(^{235}U\)
哪个每次裂变反应的能量产量更大,纯样品是大还是小\(^{235}U\)?
- 回答
-
一样


