10.5: 核反应
- Page ID
- 202202
在本节结束时,您将能够:
- 描述和比较三种类型的核辐射
- 使用核符号描述核反应期间发生的变化
- 描述重元素衰变系列所涉及的过程
早期实验揭示了三种类型的核 “射线” 或辐射:α\((\alpha)\) rays\((\beta)\) rays、β 和伽马\((\gamma)\) rays。 这三种辐射的区别在于它们穿透物质的能力。 阿尔法辐射几乎无法穿过一张薄纸。 β辐射可以穿透铝到大约 3 mm 的深度,伽马射线可以穿透铅到 2 厘米或更深的深度(图\(\PageIndex{1}\))。
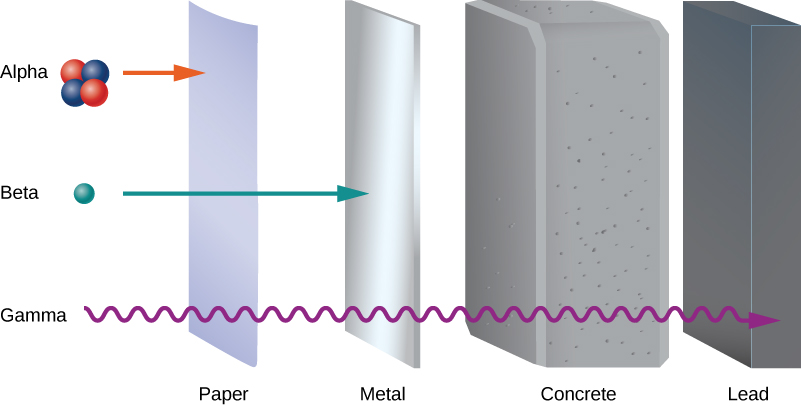
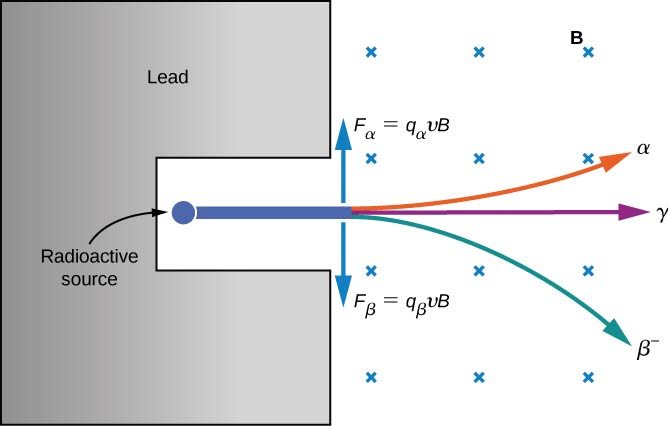
通过使这三种辐射穿过均匀的磁场来研究其电学特性,如图所示\(\PageIndex{2}\)。 根据磁场中移动电荷的磁力方程
\[\vec{F} = q\vec{v} \times \vec{B} \nonumber \]
其中带正电荷的粒子向上偏转,带负电荷的粒子向下偏转,没有电荷的粒子在没有反射的情况下穿过磁场。 最终,\(\alpha\)射线被识别为氦核\((^4He)\)、\(\beta\)带有电子和正电子(带正电荷的电子或反电子)的\(\gamma\)射线以及带有高能光子的射线。 在本节的其余部分中,我们将详细讨论 alpha、beta 和 gamma 辐射。
阿尔法衰变
沉重的不稳定原子核会发出\(\alpha\)辐射。 在\(\alpha\)-particle 衰变(或 alpha 衰变)中,原子核失去两个质子和两个中子,因此原子序数减少了二,而其质量数减少了四。 在衰变之前,原子核被称为母核。 衰变中产生的核或核被称为子核或子核。 我们用以下方式象征性地表示\(\alpha\)衰变
\[\ce{_Z^AX \rightarrow _{Z-2}^{A-4}X + _2^4He} \label{alpha} \]
其中\(_Z^AX\)是母核,\(_{Z-2}^{A-4}X\)是子核,\(_2^4He\)是\(\alpha\)粒子。 在\(\alpha\)衰变中,原子序数 Z 的原子核会衰变为原子序数\(Z - 2\)和原子质量的原核\(A - 4\)。 有趣的是,古代炼金术士将其他金属转化为金的梦想通过α衰变过程在科学上是可行的。 炼金术士的努力失败了,因为他们依赖的是化学相互作用而不是核相互作用。
观察 alpha 粒子从钯核中逸出,导致放射性 alpha 衰变。 看看随机衰减时间与半衰期有何关系。 要尝试模拟 alpha 衰变,请访问 alpha 粒子
α衰变的一个例子是铀238:
\[\ce{_{92}^{238}U \rightarrow _{90}^{234}X + _2^4He} \nonumber \]
原子序数已从92降至90。 其中的化学元素\(Z = 90\)是钍。 因此,铀238已通过\(\alpha\)粒子的发射而衰变为钍234,如上所述
\[\ce{_{92}^{238}U \rightarrow _{90}^{234}Th + _2^4He} \nonumber \]
随后,\(_{90}^{234}Th\)会因\(\beta\)排放而衰变,半衰期为24天。 这种α衰变中释放的能量以钍核和氦核的动能的形式出现,尽管钍的动能由于质量更大、速度更小而比氦小。
使用方程\(^{230}Pu\)可以找到\(\alpha\)衰减中发出的能量\(E = (\Delta m)c^2\)。 我们必须首先找到\(\Delta m\)母核和衰变产物之间的质量差异。
解决方案
衰减方程为
\[\ce{^{230}Pu \rightarrow ^{235}U + ^4He}. \nonumber \]
因此,相关的质量是\(^{230}Pu\)\(^{235}U\)、和\(\alpha\)粒子的质量或\(^4He\),所有这些都是已知的。 最初的质量是\(m(^{230}Pu) = 230.052157 \, u\)。 最终质量是总和
\[\ce{m(^{235}U) + m(^4He) = 235.043924 \, u + 4.002602 \, u} \nonumber \]
因此,
\[ \ce{\Delta m = m(^{230}Pu) - [m(^{235}U) + m(^4He)]} \nonumber \]
\[= 239.052157 \, u - 239.046526 \, u \nonumber \]
\[= 0.0005631 \, u. \nonumber \]
现在我们可以通过在方程中输入来找\(\Delta m\)到 E:
\[E = (\Delta m) c^2 = (0.005631 \, u)c^2. \nonumber \]
我们知道\(1 \, u = 931.5 \, MeV/c^2\),所以我们有
\[\begin{align} E & = (0.005631)(931.5 \, MeV/c^2)(c^2) \nonumber \\[4pt] &= 5.25 \, MeV. \nonumber \end{align} \nonumber \]
意义
这种\(\alpha\)衰变中释放的能量在兆电子伏范围内,是化学反应能的许多倍。 这些能量中的大部分变成了\(\alpha\)粒子(或\(^4He\)原子核)的动能,粒子会高速移开。 \(^{235}U\)原子核的后坐力所带走的能量要小得多,因为它的质量相对较大。 \(^{235}U\)原子核可以处于激发状态,以便以后发射光子(\(\gamma\)射线)。 239 Pu → 235 U +4 他。
测试版衰变
在大多数\(\beta\)粒子衰变(或 β 衰变)中,电子(\(\beta^-\))或正电子(\(\beta^+\))是由原子核发射的。 正电子的质量与电子相同,但其电荷是\(+e\)。 出于这个原因,正电子有时被称为反电子。 \(\beta\)衰变是如何发生的? 一个可能的解释是,电子(正电子)在衰变之前被限制在原子核中,并以某种方式逃脱。 为了获得逃逸能量的粗略估计,可以考虑一个被困在盒子(或者用量子力学术语来说是一维方井)中的电子的简化模型,其宽度相当于典型原子核(\(10^{-14}\))。 根据量子力学中的海森堡不确定性原理,电子动量的不确定性为:
\[\begin{align} \Delta p &\ge \dfrac{h}{\Delta x} \nonumber \\[4pt] &= \dfrac{6.6 \times 10^{-34} m^2 \cdot kg/s}{10^{-14}m} \nonumber \\[4pt] &= 6.6 \times 10^{-20} kg \cdot m/s. \end{align} \nonumber \]
假设这个动量值(低估)作为 “真实值”,逃逸时电子的动能大约为
\[\begin{align} \dfrac{(\Delta p)^2}{2m_e} &= \dfrac{6.6 \times 10^{-20} m^2 \cdot kg/s)^2}{2(9.1 \times 10^{-31}kg)} \nonumber \\[4pt] &= 2.0 \times 10^{-9} J \nonumber \\[4pt] &= 12,400 \, MeV. \end{align} \nonumber \]
通过实验,发现\(\beta^-\)衰变中发射的电子的动能只有几兆电子伏左右。 因此,我们得出结论,电子是在衰变中以某种方式产生的,而不是逃离原子核。 粒子产生(歼灭)由结合量子力学和相对论的理论来描述,相对论是更高级的物理学课程的主题。
核 β 衰变涉及将一个核子转化为另一个核子。 例如,中子可以通过发射电子 (\(\beta^-\)) 和称为反中微子 () 的几乎无质量的粒子而衰变为质子:\(\overline{\nu}\)
\[\ce{_0^1n \rightarrow _1^1p + _1^0e + \overline{\nu}. } \nonumber \]
该符号\(_{-1}^0e\)用于表示电子。 它的质量数为 0,因为它不是核子,其原子序数表示它的电荷为\(-e\)。\(-1\) 质子之\(_1^1p\)所以用表示,是因为它的质量数和原子序数为 1。 当这种情况发生在原子核内时,我们有以下β衰变方程:
\[\ce{_z^AX \rightarrow _{Z+1} ^AX + _1^0e + \overline{\nu}.} \label{beta} \]
这个过程是由于核力量薄弱而发生的。
观察一组原子核或单个原子核发生的 β 衰变。
例如,同位素不稳定\(_{90}^{234}Th\),会因\(\beta^-\)排放而衰变,半衰期为24天。 它的衰变可以表示为
\[\ce{_{90}^{234}Th \rightarrow _{91}^{234}X + _1^0e^+ + \overline{\nu}.} \nonumber \]
由于原子序数为 91 的化学元素是 protactinium (Pa),我们可以将钍的\(\beta^-\)衰变写成
\[\ce{_{90}^{234}Th \rightarrow _{91}^{234}Pa + _1^0e^+ + \overline{\nu}.} \nonumber \]
反向过程也是可能的:质子可以通过发射正电子而衰变为中子(\(e^+\)以及称为中子 o (\(v\)) 的几乎无质量的粒子。 这个反应写成
\[\ce{_1^1p \rightarrow _0^1n + _{+1}^0e + \nu.} \nonumber \]
正电子\(_1^0e\)与中微子一起发射\(\nu\),中子留在原子核中。 (与\(\beta^-\)衰变一样,正电子不在衰变之前,而是在衰变中产生的。) 对于孤立的质子来说,这个过程是不可能的,因为中子比质子重。 但是,这个过程在原子核内部是可能的,因为质子可以从其他核子那里获得能量来进行过渡。 举个例子,铝的同位素\(_{13}^{26}Al\)会因\(\beta^+\)排放而衰变,半衰期为\(7.40 \times 10^5 y\)。 衰减写为
\[\ce{_{13}^{26}Al \rightarrow _{12}^{26}X + _1^0e + \nu.} \nonumber \]
原子序数 12 对应于镁。 因此,
\[\ce{_{13}^{26}Al \rightarrow _{12}^{26}Mg + _1^0 e + \nu.} \nonumber \]
作为一种核反应,正电子发射可以写成
\[\ce{_Z^AX \rightarrow _{Z-1} ^AX + _1^{0} e + \nu.} \nonumber \]
在早期的\(β\)衰变实验中没有检测到中微子。 但是,能量和动量定律似乎需要这样的粒子。 后来,通过与原子核的相互作用发现了中微子。
\(_{83}^{211}Bi\)原子核会两者兼而有之\(\alpha\),然后\(\beta^-\)衰变。 对于每种情况,子核是什么?
策略
我们可以使用方程\ ref {alpha} 和方程\ ref {beta} 描述的过程以及元素周期表来识别生成的元素。
解决方案
\(\alpha\)粒子的原子序数和质量数分别为 2 和 4。 因此,当铋-211 原子核发射\(\alpha\)粒子时,子核的原子序数为 81,质量数为 207。 原子序数为 81 的元素是钍,因此衰变由下式给出
\[\ce{_{83}^{211}Bi \rightarrow _{81}^{207} Ti + _2^4He.} \nonumber \]
在\(\beta^-\)衰变中,原子序数增加 1,而质量数保持不变。 原子序数为 84 的元素是 polonium,因此衰变由下式给出
\[\ce{_{83}^{211}Bi \rightarrow _{84}^{211}Po + _{-1}^0e + \overline{\nu}.} \nonumber \]
在放射性 β 衰变中,原子质量数 A 是增加还是减少?
解决方案
都不是;它保持不变。
伽玛衰变
处于激发态的原子核可以通过发射 “伽玛射线” 光子而衰减到较低的状态,这就是所谓的伽玛衰变。 这类似于原子电子的去激发。 伽玛衰减的象征性表示为
\[\ce{_{Z}^{A}X}^{*} \ce{\rightarrow _{Z}^{A}X + \gamma} \label{gamma} \]
其中原子核上的星号 (*) 表示激发态。 在\(\gamma\)衰变中,原子序数和质量数都不改变,因此原子核的类型不会改变。
放射性衰变系列
原子核不稳定\(Z > 82\)并且会自然衰变。 这些原子核中有许多寿命很短,因此它们在自然界中找不到。 值得注意的例外包括半衰期为数\(1.39 \times 10^{10}\)年的\(_{90}^{232}Th\)(或 Th-232)和\(_{92}^{238}U\)(或 U-238)的半衰期为\(7.04 \times 10^8\)几年。 当重核衰变为较轻的子核时,较轻的子核可以成为下一次衰变的母核,依此类推。 这个过程会产生一长串的核衰变,称为衰变序列。 该系列以稳定的原子核结尾。
为了说明衰减序列的概念,请考虑 Th-232 系列的衰变(图\(\PageIndex{3}\))。 中子数 N 绘制在垂直的 y 轴上,原子数 Z 绘制在水平 x 轴上,因此 Th-232 位于坐标处\((N, Z) = (142.90)\)。 Th-232 会因\(\alpha\)排放而衰变,半衰期为数\(1.39 \times 10^{10}\)年。 Alpha 衰变使原子序数减少 2,质量数减少 4,所以我们有
\[\ce{_{90}^{232}Th \rightarrow _{88}^{228}Ra + _2^4He.} \nonumber \]
镭228的中子数为140,因此可以在图中的坐标处找到\((N,Z) = (140, \, 90)\)。 镭228也很不稳定,会因\(\alpha\)排放而衰变,Actinum-228的半衰期为5.76年。 原子序数增加 1,质量数保持不变,中子数减少 1。 请注意,在图表中,\(α\)发射显示为一条向下向左倾斜的线,N 和 Z 均减小 2。 另一方面,Beta 发射显示为一条向下向右倾斜的线,N 减少 1,Z 增加 1。 经过多次α和β衰变后,该系列以稳定的原子核Pb-208结束。
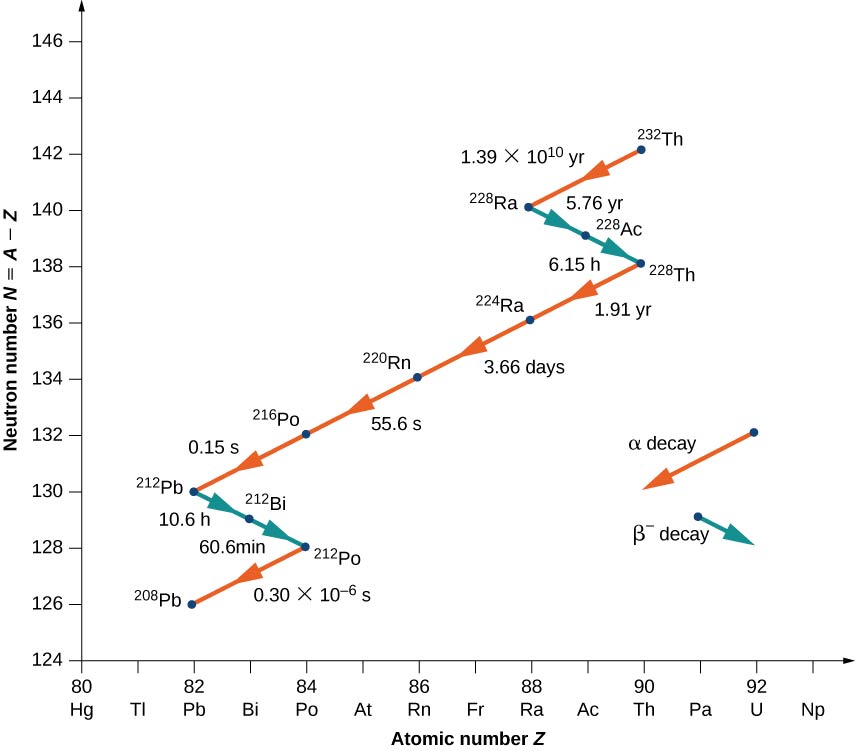
不同类型的放射性衰变(alpha、beta 和 gamma)的相对频率取决于许多因素,包括所涉及力的强度以及在不违反能量守恒和动量的情况下发生给定反应的方式的数量。 放射性衰变发生的频率通常取决于强力和电磁力的敏感平衡。
再举一个例子,以图中所示的 U-238 衰减序列为例\(\PageIndex{4}\)。 经过多次α和β衰变后,该系列以稳定的原子核Pb-206结束。
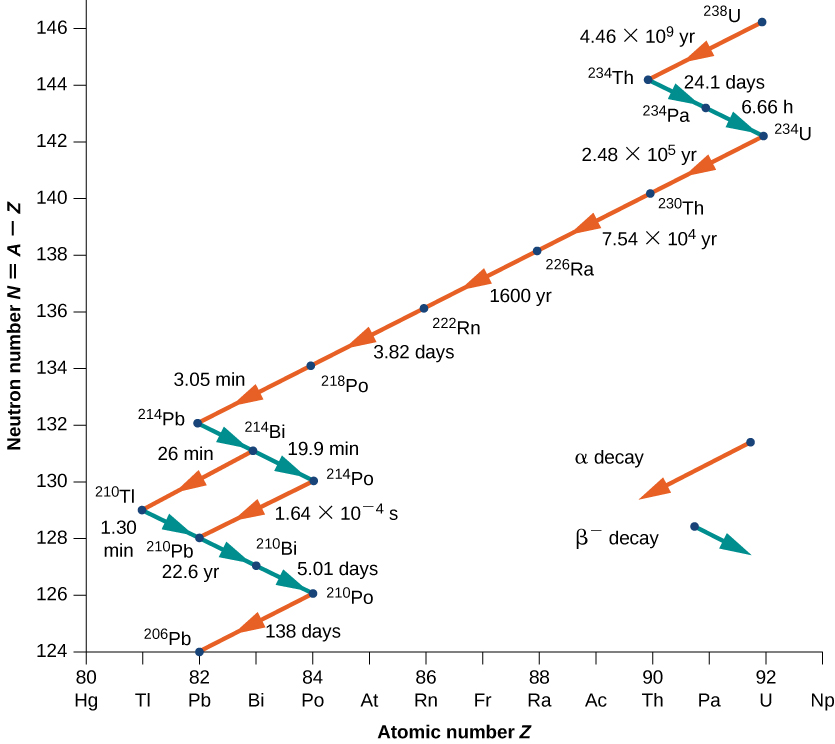
图中显示了母核不再自然存在的衰变示例\(\PageIndex{5}\)。 它以 Neptunium-237 开始,以稳定的原子核 Bismuth-209 结束。 Neptunium 之所以被称为超铀元素,是因为它不在元素周期表中的铀。 在自然界发现的所有元素中,铀的原子序数\((Z + 92)\)最高。 带有的\(Z > 92\)元素只能在实验室中生产。 它们很可能在地球形成时也存在于自然界中,但由于它们的寿命相对较短,它们已经完全腐烂了。 天然元素和人造元素之间没有根本的区别。
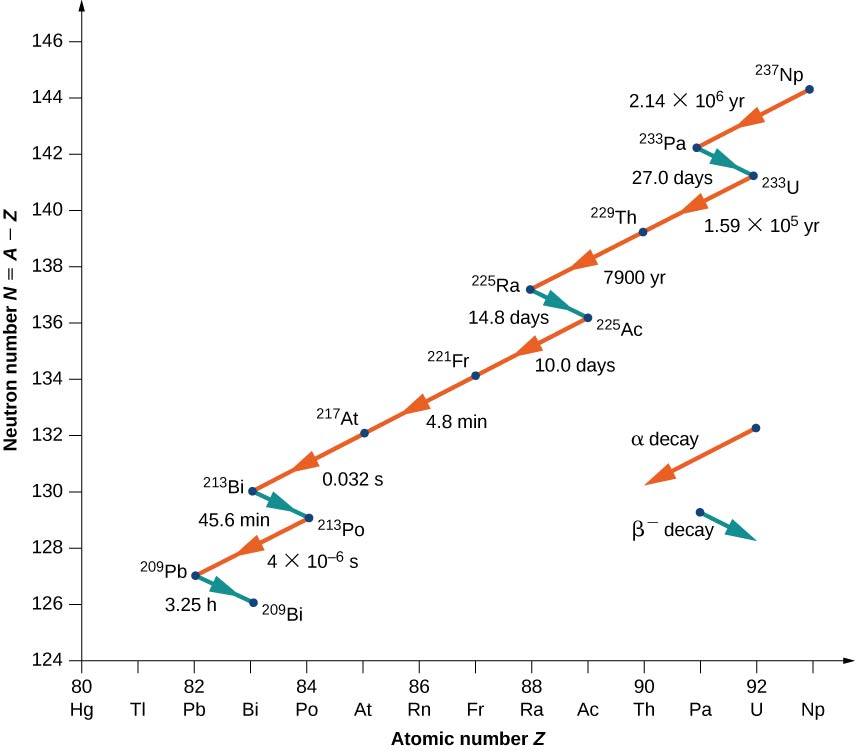
请注意,对于 Bi (21),衰减可能通过 alpha 或 beta 衰变进行。
地球中的放射性
根据地质学家的说法,如果没有热源,地球应该在不超过10亿年的时间内冷却到目前的温度。 然而,地球已有40多亿年的历史。 为什么地球冷却这么慢? 答案是核放射性,也就是说,放射性衰变中产生的高能粒子从内部加热地球(图\(\PageIndex{6}\))。
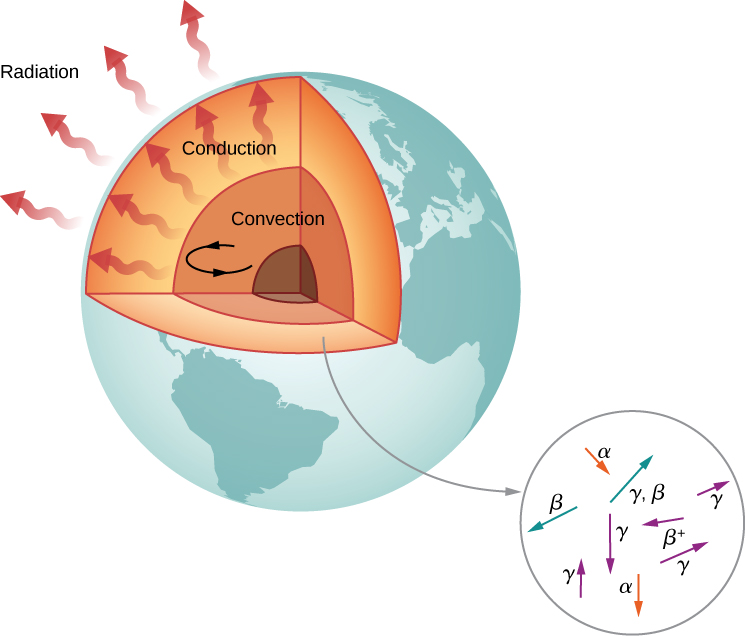
该加热模型的候选原子核是\(^{238}U\)和\(^{40}K\),其半衰期与地球年龄相似或更长。 这些衰变产生的能量(每立方米每秒钟)很小,但是能量无法轻易逸出,因此地球的核心非常热。 地球核心中的热能通过对流、传导和辐射过程转移到地球表面,并远离地表面。


