10.4: 放射性衰变
- Page ID
- 202201
在本节结束时,您将能够:
- 用衰变常数和半衰期描述放射性物质的衰变
- 使用放射性衰变定律估算物质的年龄
- 解释允许使用 14 C 对活组织进行测年的自然过程
1896年,安托万· 贝克勒尔发现富含铀的岩石会发出看不见的光线,这会使封闭容器中的照相板变暗。 科学家为这些射线的核起源提供了三个论据。 首先,辐射的影响不会因化学状态而变化;也就是说,发射材料是元素还是化合物的形式。 其次,辐射不会随温度或压力的变化而变化,这两个因素都足以影响原子中的电子。 第三,隐形射线的巨大能量(高达数百eV)与原子电子转变(只有几个 eV)不一致。 今天,这种辐射可以用原子核深处的质量转化为能量来解释。 原子核辐射的自发发射称为核放射性(图\(\PageIndex{1}\))。

放射性衰变定律
当单个原子核通过辐射发射转化为另一个原子核时,据说原子核会衰变。 所有原子核都会发生放射性衰变\(Z > 82\), 以及一些不稳定的同位素\(Z < 83\). 衰变率与物质中原始(未衰变)原子核 N 的数量成正比。 以时间间隔 dt 写入因衰变而丢失的原子核数\(-dN\)
\[-\dfrac{dN}{dt} = \lambda N \label{eq2} \]
其中\(\lambda\),称为衰减常数。 (减号表示原始原子核的数量随着时间的推移而减少。) 换句话说,可供衰变的原子核越多,衰变的次数就越多(以时间为单位)。 方程\ ref {eq2} 可以重写为
\[\dfrac{dN}{N} = -\lambda dt. \nonumber \]
对方程的两边进行积分,并定义\(N_0\)为处的原子核数\(t = 0\),我们得到
\[\int_{N_0}^N \dfrac{dN'}{N} = - \int_0^t \lambda dt'. \nonumber \]
这给了我们
\[\ln\dfrac{N}{N_0} = -\lambda t. \label{eq4} \]
以方程\ ref {eq4} 的左右两侧为幂次方程\(e\),我们就有了放射性衰变定律。
一段时间后剩余\(N\)的放射性核总数\(t\)为
\[N = N_0e^{-\lambda t} \label{decay law} \]
哪里\(\lambda\)是特定原子核的衰变常数。
核总数起初下降速度非常快,然后下降得更慢(图\(\PageIndex{2}\))。
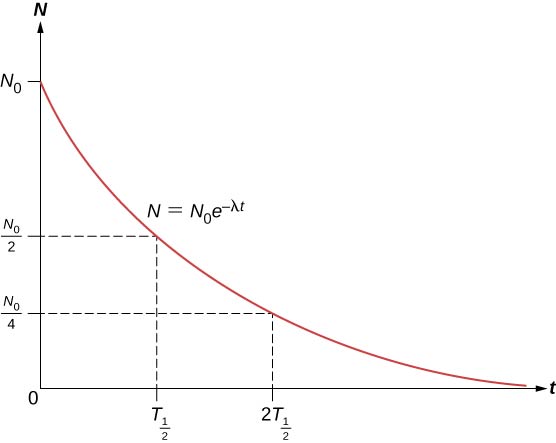
放射性物质的半衰期\((T_{1/2})\)定义为一半原始原子核衰变的时间(或原始原子核的一半剩余时间)。 不稳定同位素的半衰期显示在核素图表中。 因此,在整数 (n) 个半衰期后剩余的放射性核的数量为
\[N = \dfrac{N_0}{2^n} \label{eq5} \]
如果衰减常数\((\lambda)\)很大,则半衰期很小,反之亦然。 要确定这些数量之间的关系,请注意何\(t = T_{1/2}\)时\(N = N_0/2\)。
因此,方程\ ref {eq5} 可以重写为
\[\dfrac{N_0}{2} = N_0e^{-\lambda T_{1/2}}. \nonumber \]
将两边除以\(N_0\)然后取自然对数得出
\[\ln \dfrac{1}{2} = \ln \, e^{-\lambda T_{1/2}} \nonumber \]
这简化为
\[\lambda = \dfrac{0.693}{T_{1/2}}. \nonumber \]
因此,如果我们知道放射性物质的半衰期 T 1/2,我们就能找到其衰变常数。 放射\(\overline{T}\)性物质的寿命定义为原子核在衰变之前存在的平均时间。 物质的寿命只是衰减常数的倒数,写成
\[\overline{T} = \dfrac{1}{\lambda}. \nonumber \]
活动 A 定义为衰减率的大小,或
\[A = -\dfrac{dN}{dt} = \lambda N = \lambda N_0 e^{-\lambda t}. \nonumber \]
时间间隔 dt 中的无穷小变化 d N 为负数,因为父粒子(未衰变)的数量正在减少,因此活性(A)为正。 将初始活动定义为\(A_0 = \lambda N_0\),我们有
\[A = A_0 e^{-\lambda t}. \label{eq8} \]
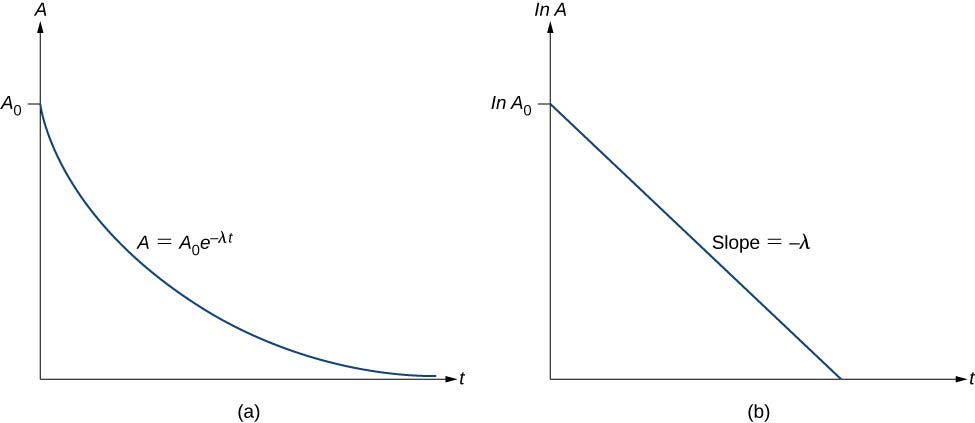
因此,放射性物质的活性A随着时间的推移呈指数级降低(图\(\PageIndex{3}\))。
锶-90的半衰期为28.8 y。找出 (a) 其衰变常数和 (b) 1.00 g 材料的初始活度。\(\ce{_{38}^{90}Sr}\)
策略
我们可以直接从方程\ ref {eq8} 中找到衰减常数。 为了确定活性,我们首先需要找到存在的原子核数量。
解决方案
a. 发现衰减常数为
\[\lambda = \dfrac{0.693}{T_{1/2}} = \left(\dfrac{0.693}{T_{1/2}}\right)\left(\dfrac{1 \, yr}{3.16 \times 10^7 \, s}\right) = 7.61 \times 10^{-10} \, s^{-1}. \nonumber \]
b. 的原子质量\(_{38}^{90}Sr\)为 89.91 g。使用 Avogadro 的数字\(N_A = 6.022 \times 10^{23}\) atoms/mol,我们可以找出 1.00 g 材料中原子核的初始数量:
\[N_0 = \dfrac{1.00 \, g}{89.91 \, g} (N_A) = 6.70 \times 10^{21} \, nuclei. \nonumber \]
由此,我们发现 1.00 g 锶-90 的活\(A_0\)性为\(t = 0\)
\[A_0 = \lambda N_0 = (7.61 \times 10^{-10} s^{-1})(6.70 \times 10^{21} \, nuclei) = 5.10 \times 10^{12} \, decays/s. \nonumber \]
用物质的半衰期来表达\(\lambda\),我们得到
\[A = A_0 e^{-(0.693/T_{1/2})T_{1/2}} = A_0 e^{-0.693} = A_0/2. \label{eq11} \]
因此,活性在半衰期后减半。 我们可以\(\lambda\)通过测量活动随时间变化来确定衰减常数。 取方程\ ref {eq11} 左右两侧的自然对数,我们得到
\[\ln \, A = - \lambda t + \ln \, A_0. \nonumber \]
该方程遵循线性形式\(y = mx + b\)。 如果我们绘制\ ln A 与 t 的对比,则预计会有一条具有斜率\(-\lambda\)和 y 截距的直线\(\ln \, A_0\)(图\(\PageIndex{3b}\))。 活动 A 以贝克勒尔 (Bq) 为单位表示,其中 1\(1 \, Bq = 1 \, decay \, per \, second\)。 这个数量也可以用每分钟的衰减数或每年的衰减来表示。 最常见的活动单位之一是居里(Ci),定义为 1 g 的活性\(^{226}Ra\)。 Bq 和 Ci 之间的关系是
\[1 \, Ci = 3.70 \times 10^{10}Bq. \nonumber \]
按质量\(20\%\)计算,人体的大约是碳。 计算在活生物体\(^{14}C\)中发现的 1.00 千克碳所产生的活性。 以 Bq 和 Ci 为单位表示活动。
策略
的活性\(^{14}C\)使用方程确定\(A_0 = \lambda N_0\),其中 λ 是衰变常数,\(N_0\)是放射性原子核的数量。 1.00 kg 样品中的\(^{14}C\)核数目分两步确定。 首先,我们使用摩尔概念来确定\(^{12}C\)原子核的数量。 其次,我们将该值乘以\(1.3 \times 10^{-12}\)(活生物体碳样本\(^{14}C\)中的已知丰度),以确定活生物体中\(^{14}C\)原子核的数量。 衰减常数是根据已知的半衰期确定的\(^{14}C\)(可从 [链接] 获得)。
解决方案
一摩尔碳的质量为12.0 g,因为它几乎是纯净的\(^{12}C\)。 因此,千克中碳核的数量为
\[N(^{12}C) = \dfrac{6.02 \times 10^{23} mol^{-1}}{12.0 \, g/mol} \times (1000 \, g) = 5.02 \times 10^{25}. \nonumber \]
因此,1 kg 碳中的\(^{14}C\)原子核数为
\[N(^{14}C) = (5.02 \times 10^{25})(1.3 \times 10^{_12}) = 6.52 \times 10^{13}. \nonumber \]
现在我们可以使用方程式\ ref {eq11} 找到活动\(A\)了。 输入已知值可以给我们
\[A = \dfrac{0.693 (6.52 \times 10^{13})}{5730 \, y} = 7.89 \times 10^9 \, y^{-1} \nonumber \]
或每年\(7.89 \times 10^9\)衰变。 要将其转换为单位 Bq,我们只需将年转换为秒即可。 因此,
\[A = (7.89 \times 10^9 \, y^{-1}) \dfrac{1.00 \, y}{3.16 \times 10^7 \, s} = 250 \, Bq, \nonumber \]
或者每秒 250 次衰变。 要用居里表达 A,我们使用居里的定义,
\[A = \dfrac{250 \, Bq}{3.7 \times 10^{10} \, Bq/Ci} = 6.76 \times 10^{-9} Ci. \nonumber \]
因此,
\[A = 6.76 \, nCi. \nonumber \]
意义
按重量计算,大约\(20\%\)人体是碳。 人体每秒发生数百次\(^{14}C\)衰变。 Carbon-14和体内其他天然存在的放射性物质构成了人暴露于核辐射的背景情况。 正如我们将在本章后面看到的那样,该活性水平远低于最大推荐剂量。
放射性约会
放射性测年法是一种利用自然产生的放射性来确定材料年龄的技术, 例如岩石或古代人工制品. 基本方法是估计材料中原子核的原始数量和材料中的当前原子核数量(衰变后),然后使用衰减常数的已知值\(\lambda\)和方程\ ref {衰变定律} 来计算衰变的总时间\(t\)。
放射性测年的一种重要方法是碳14测年. 当高能太阳辐射撞击高层大气中的\(^{14}N\)原子核,随后衰变时,会产生碳14核,半衰期为5730年。 放射性碳与稳定碳具有相同的化学成分,因此它与生态圈结合,最终成为每个活生物体的一部分。 Carbon-14的丰度为每万亿中普通碳的1.3部分。 因此,如果您知道物体中碳核的数量,则将该数字乘\(1.3 \times 10^{-12}\)以得出该物体中的\(^{14}C\)原子核数量。 当生物死亡时,与环境的碳交换就会停止,\(^{14}C\)并且在衰变时不会得到补充。
通过将人工制品(例如木乃伊包装)\(^{14}C\)中的丰度与活组织中的正常丰度进行比较,可以确定木乃伊的年龄(或人死后的时间)。 Carbon-14测年法可用于历史可达50,000年的生物组织,但通常对于较年轻的样本最为准确,因为其中\(^{14}C\)原子核的丰度更高。 非常古老的生物材料\(^{14}C\)根本不含任何物质。 碳定年的有效性可以通过其他方式进行检查,例如通过历史知识或树木年轮计数。
在一个古老的墓穴中,您的考古学家团队发现了古老的木制家具。 只有\(80\%\)原件\(^{14}C\)留在木头里。 家具多久了?
策略
问题陈述暗示了这一点\(N/N_0 = 0.80\)。 因此,我们重新排列方程\ ref {衰减定律} 以找到乘积\(\lambda t\)。 我们知道的半衰期\(^{14}C\)为 5730 y,因此我们也知道衰减常数,因此也知道总衰减时间\(t\)。
解决方案
我们重新排列方程\ ref {衰减定律} for to g\(N/N_0\) ives
\[\dfrac{N}{N_0} = e^{-\lambda t}. \nonumber \]
因此
\[0.80 = e^{-\lambda t}. \nonumber \]
取两边的自然对数得出
\[\ln \, 0.80 = - \lambda t,\nonumber \]
所以
\[-0.223 = -\lambda t. \nonumber \]
重新排列方程以隔离\(t\)可以给我们带来好处
\[t = \dfrac{0.223}{\left(\dfrac{0.693}{5730 \, y}\right)} = 1844 \, y. \nonumber \]
意义
这些家具已有将近 2000 年的历史——这是一个令人印象深刻的发现。 碳14测年的典型不确定性差不多\(5\%\),因此家具的使用年限在1750至1950年之间。 该日期范围必须得到其他证据(例如历史记录)的确认。
放射性核素的衰变率很高。 这对它的半衰期和活性意味着什么?
- 回答
-
半衰期与衰减率成反比,因此半衰期很短。 活性既取决于衰变粒子的数量,也取决于衰减率,因此活性可以很大,也可以很小。
访问放射性约会游戏以了解放射性测年的类型,并尝试对一些古代物体进行测年.


