Skip to main content
Global

10.3: 核结合能

  1. Last updated
  2. Save as PDF
  • Page ID
    202269

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 计算各种原子核的质量缺陷和结合能
    • 使用每核子结合能 (BEN) 与质量数 (A) 图表来评估原子核的相对稳定性
    • 将原子核中核子的结合能与原子中电子的电离能进行比较

    在原子核中将核子结合在一起的力远大于通过静电吸引将电子与原子结合的力。 原子核和原子（分别为\(10^{-15}\)和\(10^{-10}\) m）的相对大小就证明了这一点。 因此，从原子核中撬出核子所需的能量远大于移除（或电离）原子中电子所需的能量。 总的来说，所有核变化都涉及每个发生反应的粒子的大量能量。 这有许多实际应用。

    质量缺陷

    根据核粒子实验，原子核的总质量小\((m_{nuc})\)于其组成核子（质子和中子）的质量之和。 质量差或质量缺陷由下式给出

    \[\Delta m = Zm_p + (A - Z)m_n - m_{nuc} \label{mass defect} \]

    其中\(Zm_p\)是质子的总质量，\((A - Z)m_n\)是中子的总质量，\(m_{nuc}\)是原子核的质量。 根据爱因斯坦的狭义相对论，质量是衡量系统总能量的量度 (\(E = mc^2\))。 因此，原子核的总能量小于其组成核子的能量之和。 因此，从孤立的质子和中子系统中形成原子核是一种放热反应，这意味着它会释放能量。 在此过程中发射或辐射的能量为\((\Delta m)c^2\)。

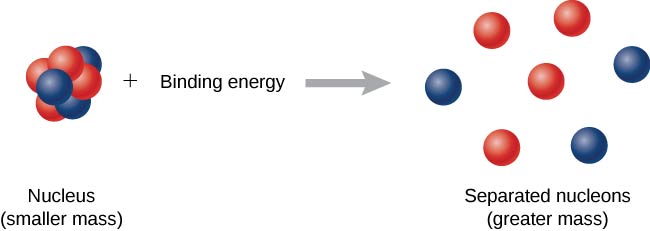
    该图显示了反应。 LHS 显示原子核加上结合能。 这个原子核是一团紧密包装的质子和中子，被标记为较小的质量。 RHS 上有一个原子核，质子和中子包装松散，有标记，分离的核子，质量更大。
    图\(\PageIndex{1}\)：结合能是将原子核分解成其组成质子和中子所需的能量。 分离的核子系统的质量大于结合的核子系统的质量。

    现在想象一下这个过程是相反的。 不是形成原子核，而是向系统注入能量来分解原子核（图\(\PageIndex{1}\)）。 所需的能量称为总结合能 (BE)\(E_b\)。

    定义：结合能量

    结合能等于形成原子核时释放的能量，因此由下式给出

    \[E_b = (\Delta m)c^2. \label{BE} \]

    实验结果表明，具有质量数\(A > 8\)的原子核的结合能与原子核 A 中的核子总数大致成正比。 例如\((^{24}Mg)\)，镁核的结合能大约是碳核的两倍\((^{12}C)\)。

    示例\(\PageIndex{1}\): Mass Defect and Binding Energy of the Deuteron

    计算氘的质量缺陷和结合能。 氘的质量是\(m_D = 3.34359 \times 10^{-27}kg\)或\(1875.61 \, MeV/c^2\)。

    解决方案

    对于 deuteron\(Z=1\) 和\(A=2\). 根据方程\ ref {质量缺陷}，氘的质量缺陷为

    \[\begin{align*} \Delta m &= m_p + m_n - m_D \\[4pt] &= 938.28 \, MeV/c^2 + 939.57 \, MeV/c^2 - 1875.61 \, MeV/c^2 \\[4pt] &= 2.24 \, MeV/c^2. \end{align*} \nonumber \]

    那么，氘的结合能就是

    \[\begin{align*} E_b &= (\Delta m)c^2 \\[4pt] &= (2.24 \, MeV/c^2)(c^2) \\[4pt] &= 2.24 \, MeV. \end{align*} \nonumber \]

    将氘分解成质子和中子需要超过两百万的电子伏特。 这个非常大的值表明了核力量的强大力量。 相比之下，通过有吸引力的库仑力（一种电磁力）释放与氢原子结合的电子所需的最大能量约为10 eV。

    每个核子的结合能图

    在核物理学中，最重要的实验量之一是每核子结合能 (BEN)，其定义为

    \[BEN = \dfrac{E_b}{A} \label{BEN} \]

    这个量是从原子核中移除单个核子所需的平均能量，类似于原子中电子的电离能。 如果 BEN 相对较大，则原子核相对稳定。 BEN 值是根据核散射实验估算得出的。

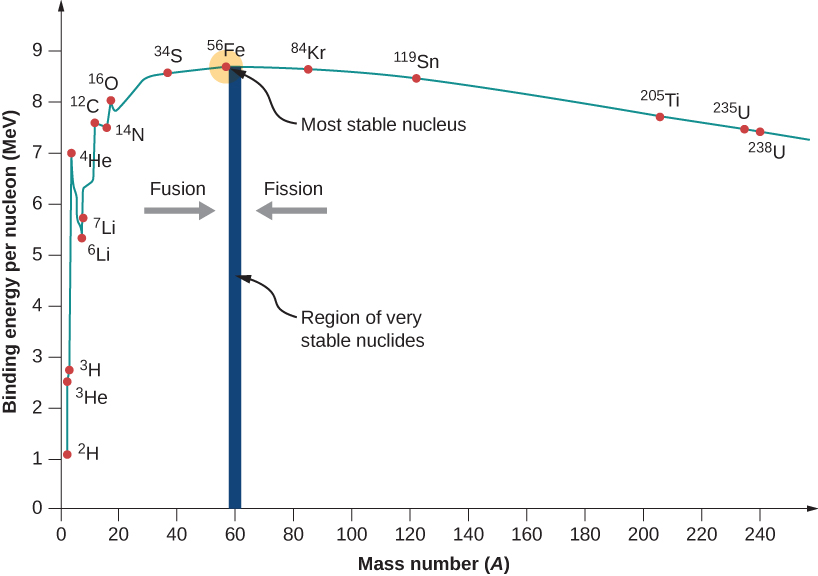
    图中给出了每个核子的结合能与原子序数 A 的对比图\(\PageIndex{2}\)。 许多物理学家认为这张图是物理学中最重要的图表之一。 按顺序排列了两个音符。 首先，典型的 BEN 值在 6—10 兆电子伏之间，平均值约为 8 兆电子伏。 换句话说，从典型的原子核中撬出一个核子需要数百万电子伏特，而在氢气基态下电离电子仅需13.6 eV。 这就是为什么核力量被称为 “强大” 核力量的原因。

    其次，图表在低 A 处上升，峰值非常接近铁\((Fe, \, A = 56)\)，然后在高点逐渐变细\(A\)。 峰值表明铁核是自然界中最稳定的原子核（这也是恒星核心中的核聚变以铁结尾的原因）。 图表上升和逐渐缩小的原因与原子核中的竞争力量有关。 在低值时\(A\)，核子之间的有吸引力的核力比质子之间的排斥性静电力占主导地位。 但是在高值时\(A\)，力之间的排斥性静电力开始占主导地位，这些力往往会分解原子核而不是将其固定在一起。

    每个核子的结合能、meV 与质量数的对比图 A。该图起点接近点 2,1，峰值接近元素 56 Fe，后者的兆电子伏值介于 8 到 9 之间。 此后，该图逐渐变为大约 7. 56 Fe 被标记为最稳定的原子核。 A = 60 处的竖线标记为非常稳定的核素区域。 这个栏的两边都有一个指向它的箭头。 左边的标记为聚变，右边的标记为裂变。
    图\(\PageIndex{2}\)：在这张稳定核每个核子的结合能图中，质量接近的原子核的 BEN 最大\(^{56}Fe\)。 因此，质量数远小于铁的原子核聚变以及质量数大于铁的原子核的裂变都是放热过程。

    正如我们将看到的，Ben-vers-A 图表示原子核分裂或组合会释放大量能量。 这是各种现象的基础，从核电厂的发电到阳光。

    示例\(\PageIndex{2}\): Tightly Bound Alpha Nuclides

    计算一个核子的每个核子的结合能\(^4He \, (\alpha \, particle)\).

    策略

    使用方程确定总结合能 (BE)\(BE = (\Delta m)c^2\)，其中\(\Delta m\)是质量缺陷。 每个核子的结合能 (BEN) 除以\(A\)（方程\ ref {BEN}）。

    解决方案

    因为\(^4He\)，我们有\(Z = N = 2\)。 总结合能（方程\ ref {BE}）为

    \[BE = {[2m_p + 2m_n] - m(^4He)}c^2. \nonumber \]

    这些群众是\(m(^4He) = 4.002602 \, u\)\(m_p = 1.007825 \, u\)、和\(m_n = 1.008665 \, u\)。 因此，我们有

    \[BE = (0.030378 \, u)c^2. \nonumber \]

    注意到这一点\(1 \, u = 931.5 \, MeV/c^2\)，我们发现

    \[\begin{align*} BE &= (0.030378)(931.5 \, MeV/c^2)c^2 \\[4pt] &= 28.3 \, MeV. \end{align*} \nonumber \]

    因为\(A = 4\)，每个核子的总结合能（方程\ ref {BEN}）为

    \[BEN = 7.07 \, MeV/nucleon. \nonumber \]

    意义

    请注意，每个核子的结合能远大于氢同位素的结合能 (\(\approx 3 \, MeV/nucleon\))。\(^4He\) 因此，如果不向系统注入能量，氦核就无法分解氢同位素。

    练习\(\PageIndex{2}\)

    如果每个核子的结合能很大，这是否会使从原子核上剥离核子变得更难或更容易？

    回答

    更难的