Skip to main content
Global

10.2: 原子核的特性

  1. Last updated
  2. Save as PDF
  • Page ID
    202217

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 描述原子核的组成和大小
    • 使用核符号表示原子核的组成
    • 解释为什么重核中的中子数大于质子
    • 根据元素的同位素计算元素的原子质量

    原子核由质子和中子组成（图\(\PageIndex{1}\)）。 质子和中子的质量大致相同，但质子携带一个单位的正电荷（+e），而中子不携带电荷。 这些粒子聚集在原子中心的极小空间中。 根据散射实验，原子核的形状为球形或椭球体，大小约为氢原子的1/100,000。 如果原子的大小相当于美国职棒大联盟体育场的大小，那么原子核的大小将大致相当于棒球的大小。 原子核内的质子和中子被称为核子。

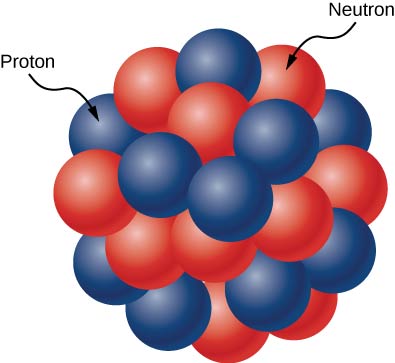
    该图显示了一组紧密聚集在一起的红色和蓝色球体。 红色球体被标记为中子，蓝色的球体被标记为质子。
    图\(\PageIndex{1}\)：原子核由质子和中子组成。 质子以蓝色显示，中子以红色显示。

    核子计数

    原子核中的质子数由原子序数给出\(Z\)。 原子核中的中子数是中子数,\(N\). 核子的总数是质量数,\(A\). 这些数字的相关性为

    \[A = Z + N. \nonumber \]

    原子核象征性地表示为

    \[_Z^AX, \nonumber \]

    其中，\(X\)代表化学元素，\(A\)是质量数，\(Z\)是原子序数。 例如，\(_6^{12}C\)表示具有六个质子和六个中子（或 12 个核子）的碳核。

    图中显示了一系列稳定核（核素 s）中子数 \(Z\)N 与质子数量的对比图\(\PageIndex{2}\)。 对于给定的值\(Z\)，可以有多个值\(N\)（蓝点）。 对于较小的值\(Z\)，中子的数量等于质子的数量\((N = P)\)，数据落在红线上。 对于较大的值\(Z\)，中子的数量大于质子的数量，\((N > P)\)并且数据点落在红线以上。 中子的数量通常大于质子的数量\(Z > 15\)。

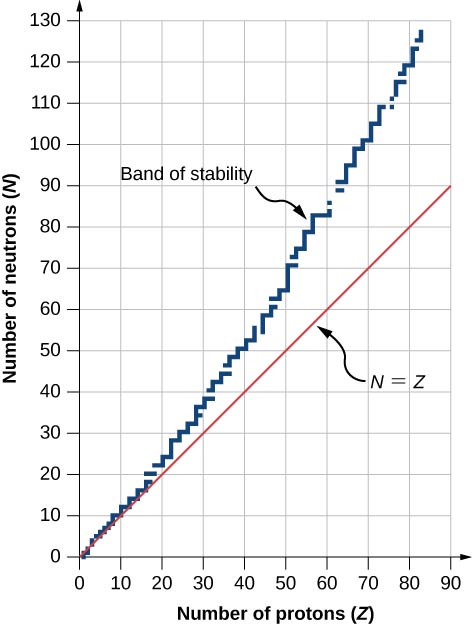
    显示中子数量的图表，N 与质子数 Z。图上的一条直线标记为 N 等于 Z。另一条锯齿线被标记为稳定带。 这有渐进的步骤。 它从原点开始。 Z = 80 时，N 的值为 120。
    图\(\PageIndex{2}\)：这张图绘制了稳定原子核的中子数 N 与质子 Z 的数量。 原子核越大，中子比质子多。

    图中给出了基于该图的图表，该图提供了有关每个原子核的更多详细信息\(\PageIndex{3}\)。 这个图表被称为核素图表。 每个细胞或图块代表一个单独的核。 原子核按上升 Z（沿水平方向）和上升 N（沿垂直方向）的顺序排列。

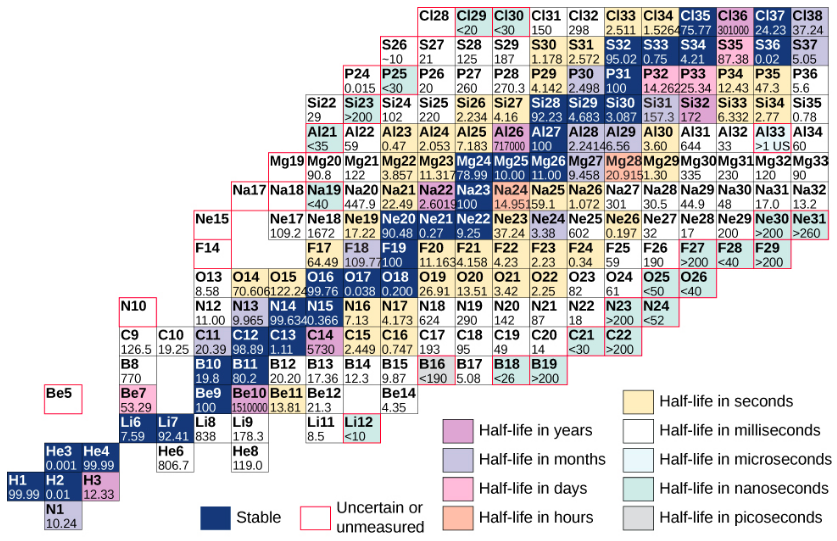    该图显示了核素的图表，沿水平方向上升的 Z，沿垂直方向上升的 N。 图表中心沿对角线的单元格采用颜色编码，表示它们是稳定的。图\(\PageIndex{3}\)：核素的部分图。 对于稳定的原子核（深蓝色背景），细胞值表示在地球上发现的具有相同原子序数（丰度百分比）的原子核的百分比。 对于不稳定的原子核，该数字代表半衰期。

    含有质子数 (Z) 和不同数量中子 (N) 的原子被称为同位素。 例如，氢有三种同位素：普通氢气（1 个质子，没有中子）、氘气（一个质子和一个中子）和钍（一个质子和两个中子）。 给定原子的同位素具有相同的化学性质，因为这些特性是由原子外部电子之间的相互作用决定的，而不是由核子之间的相互作用决定的。 例如，含有氘而不是氢气的水（“重水”）的外观和味道都像普通水。 下表显示了常见同位素的列表。

    表\(\PageIndex{1}\)：常见同位素
    元素 符号 质量编号 质量（原子质量单位） 丰度百分比* 半衰期**
    氢气 H 1 1.0078 99.99 稳定
    \(^2H\)或者是 D 2 2.0141 0.01 稳定
    \(^3H\) 3 3.0160 - 12.32 y
    碳 \(^{12}C\) 12 12.0000 98.91 稳定
    \(^{13}C\) 13 13.0034 1.1 稳定
    \(^{14}C\) 14 14.0032 - 5730 y
    氮气 \(^{14}N\) 14 14.0031 00.6 稳定
    \(^{15}N\) 15 15.001 0.4 稳定
    \(^{16}N\) 16 16.0061 - 7.13 s
    氧气 \(^{16}O\) 16 15.0040 99.76 稳定
    \(^{17}O\) 17 16.9991 0.04 稳定
    \(^{18}O\) 18 17.9992 0.20 稳定
    \(^{19}O\) 19 19.0035 - 26.46 s
    *如果小于 0.001（微量量），则不可输入。 **如果半衰期 > 10 秒，则稳定。

    为什么在较重的原子核中，中子的数量超过质子（图\(\PageIndex{3}\)）？ 这个问题的答案需要了解原子核内部的力，其中有两个主要力在起作用：

    1. 使带正电荷的质子相互排斥的远程静电（库仑）力；以及
    2. 使原子核中的所有核子相互吸引的短程强核力量。

    你可能还听说过 “弱” 的核力量。 这种力量是造成一些核衰变的原因，但顾名思义，它在稳定原子核免受其所经历的强烈库仑排斥方面没有发挥作用。 在下一章介绍粒子物理学时，我们将更详细地讨论强大的核力量。 当核子之间的吸引力补偿了原子核中所有质子之间的排斥性远程静电力时，就会产生核稳定性。 对于重核，过\((Z > 15)\)量的中子是必要的，以防止静电相互作用将原子核分开，如图所示\(\PageIndex{4}\)。

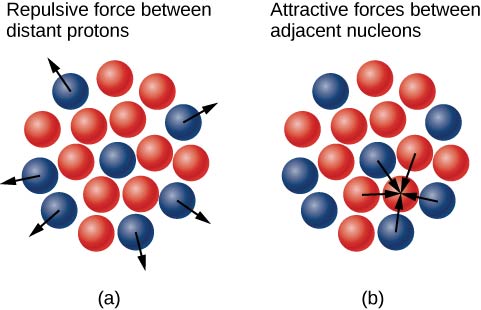
    图 a 显示了一组红色和蓝色的小圆圈。 中心有一个蓝色的质子，周围环绕着红色中子。 外围有更多的质子，它们的箭头指向外部。 图 b 显示了同一个集群。 箭头显示质子和中子都被吸引到相邻的中子上。
    图\(\PageIndex{4}\)：(a) 静电力具有排斥性，射程长。 箭头表示中心质子（也用蓝色）对核表面质子（蓝色）施加的向外力。 (b) 强大的核力量在相邻的核子之间起作用。 箭头代表中子（红色）对其最近的邻居施加的吸引力。

    由于存在稳定的同位素，我们在引用元素的质量时必须特别小心。 例如，铜 (Cu) 有两个稳定的同位素：

    \[_{29}^{63} Cu ( 62.929595 \, g/mol) \, with \, an \, abundance \, of \, 69.09\% \nonumber \]

    \[_{29}^{65} Cu ( 64.927786 \, g/mol) \, with \, an \, abundance \, of \, 30.91\% \nonumber \]

    鉴于铜的这两个 “版本”，这种元素的质量是多少？ 元素的原子质量被定义为其同位素质量的加权平均值。 因此，铜的原子质量为

    \[m_{Cu} = (62.929595)(0.6909) + (64.927786)(0.3091) = 63.55 \, g/mol. \nonumber \]

    单个原子核的质量通常以原子质量单位 s (u) 表示，其中\(u = 1.66054 \times 10^{-27} kg\)。 （原子质量单位定义为\(^{12}C\)原子核质量的1/12。） 在原子质量单位中，氦核 (A = 4) 的质量约为 4 u。氦核也被称为 alpha (α) 粒子。

    核大小

    最简单的原子核模型是一个密集的核子球体。 因此，原子核\(V\)的体积与核子的数量成正比\(A\)，表示为

    \[V = \dfrac{4}{3} \pi r^3 = kA, \nonumber \]

    其中，\(r\)是原子核的半径，\(k\)是以体积为单位的常数。 求解\(r\)，我们有

    \[r = r_0 A^{1/3} \label{radius} \]

    其中\(r_0\)是常数。 对于氢气\((A = 1)\)，\(r_0\)对应于单个质子的半径。 散射实验支持各种原子核的这种一般关系，它们意味着中子的半径与质子大致相同。 实验测得的值约\(r_0\)为 1.2 femtometer（回想一下\(1 \, fm = 10^{-15}m\)）。

    示例\(\PageIndex{1}\): The Iron Nucleus

    找出 Fe-56 原子核\((\rho)\)的半径 (r) 和近似密度。 假设 Fe-56 原子核的质量约为 56 u。

    策略

    1. 给定，找到的半径\(^{56}Fe\)是简单的应用\(A = 56\)。\(r = r_0A^{1/3}\)
    2. 要找到这个原子核的近似密度，假设原子核是球形的。 使用在 (a) 部分中找到的半径计算其体积，然后从中找到其密度\(\rho = m/V\)。

    解决方案

    1. 原子核的半径由方程\ ref {radius} 给出。 将值替换为 A\(r_0\) 得到\[\begin{align} r &= (1.2 \, fm)(56)^{1/3} \nonumber \\[4pt] &= (1.2 \, fm)(3.83) \nonumber \\[4pt] &= 4.6 \, fm.\nonumber \end{align} \nonumber \]
    2. 我们发现，密度被定义为\(\rho = m/V\)，对于半径为 r 的球体，用已知值\[\rho = \dfrac{m}{V} = \dfrac{m}{(4/3)\pi r^3}. \nonumber \]代替已知值\[\begin{align} \rho &= \dfrac{56 \, u}{(1.33)(3.14)(4.6 \, fm)^3} \nonumber \\[4pt] &= 0.138 \, u/fm^3. \nonumber \end{align} \nonumber \]得出 Converting 为单位\(kg/m^3\)\[\begin{align} \rho &= (0.138 \, u/fm^3)(1.66 \times 10^{-27} kg/u)\left(\frac{1 \, fm}{10^{-15}m}\right) \nonumber \\[4pt] &= 2.3 \times 10^{17} \, kg/m^3. \nonumber \end{align} \nonumber \]

    意义

    1. 发现 Fe-56 原子核的半径约为 5 fm，因此其直径约为 10 fm，或\(10^{-14} m\)。 在之前关于卢瑟福散射实验的讨论中，据估计，轻核的直径为\(10^{-15}m\)轻核。 因此，显示的中型原子核的结果是合理的。
    2. 这里发现的密度可能看起来令人难以置信。 但是，这与先前关于原子核在很小的太空区域中包含几乎所有质量的原子的评论一致。 一立方米的核物质的质量与每边61千米的立方水的质量相同。
    练习\(\PageIndex{1}\)

    核 X 比核 Y 大两倍。它们的原子质量的比例是多少？

    回答

    八