Skip to main content
Global

9.6: 固体波段论

  1. Last updated
  2. Save as PDF
  • Page ID
    201937

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 描述确定晶体中电子能级的两种主要方法
    • 解释晶体能量结构中是否存在能带和间隙
    • 解释为什么有些材料是好的导体而另一些是好的绝缘体
    • 区分绝缘体和半导体

    自由电子模型解释了导体的许多重要特性，但至少在两个方面很弱。 首先，它假设固体内部存在恒定的势能。 （回想一下，恒定势能与无力有关。） 该图\(\PageIndex{1}\)将恒定势能（虚线）的假设与周期性库仑势进行了比较，后者\(-1/r\)在每个晶格点处下降，其中 r 是与离子核的距离（实线）。 其次，自由电子模型假设表面存在无法穿透的屏障。 这种假设是无效的，因为在某些条件下，电子可以逃离表面，例如在光电效应中。 除了这些假设之外，自由电子模型并不能解释导体、半导体和绝缘体在电子特性上的巨大差异。 因此，需要一个更完整的模型。

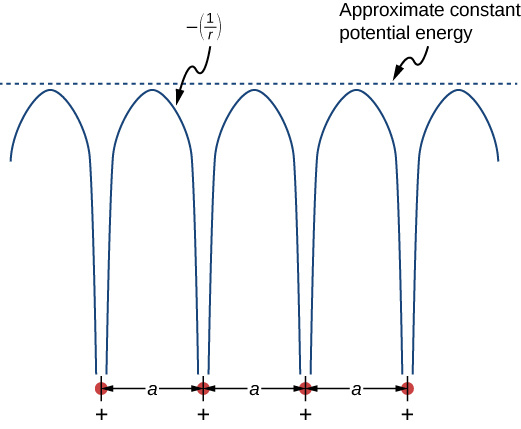
    该图显示了连续三个倒置的 U 形结构，两行两侧有两个不完整的结构。 两个连续数字之间的底部有红点，下方有加号。 两个连续点之间的距离为 a。形状以 r 标记为负 1。形状正上方有一个虚线。 这被标记为近似恒定势能。
    图\(\PageIndex{1}\)：用于模拟导体中电子的周期电位。 固体中的每个离子都是库仑电位的来源。 请注意，自由电子模型是富有成效的，因为该场的平均值大致恒定。

    我们可以通过求解 Schrödinger 的周期电位方程来生成改进的模型，如图所示\(\PageIndex{1}\)。 但是，该解决方案要求的技术数学远远超出了我们的范围。 我们再次寻求基于量子力学的定性论据，以找到前进的方向。

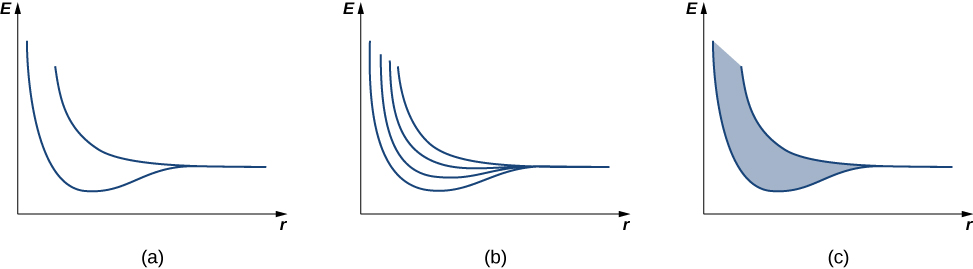
    我们首先回顾一下用于解释共价键能量结构的论点。 假设两个相同的氢原子相距太远，以至于它们之间没有任何相互作用。 进一步假设每个原子中的电子处于相同的基态：能量为\(-13.6 \, eV\)（忽略自旋）的 1 s 电子。 当氢原子靠得更近时，电子的单个波函数会重叠，根据排除原理，它们不能再处于同一个量子态，这会将原来的等效能级分成两个不同的能量级。 这些等级的能量取决于原子间距离，\(a\)（图\(\PageIndex{2a}\)）。

    如果将四个氢原子聚集在一起，则由四个可能的对称性形成四个等级——每个井中有一个正弦波 “驼峰”，上下交替出现，依此类推。 在大量 N 个原子的极限内，我们预计固体中几乎连续的电子能级带会扩散（图\(\PageIndex{2c}\)）。 这些波段中的每一个都被称为能量带。 （从技术上讲，允许的能量和波数状态仍然是量化的，但是对于大量的原子，这些态之间的距离非常接近，以至于它们被认为是连续的或 “连续的”。）

    图中显示了 E 与 R 的三张图表。 图 a 有一条由两条几乎垂直的线条形成的曲线，它们向下移动，向右转，几乎变成水平线。 它们汇聚成一条线。 图 b 有一条相似的曲线，但图 a 中的线之间还有另外两条线。图 c 与图 a 类似，两条线之间的区域为阴影。
    图\(\PageIndex{2}\)：能级分裂对（a）两个原子，（b）四个原子和（c）大量原子之间的平均距离的依赖性。 对于大量电子，会产生连续的能量带

    能带所容纳的电子数量不同。 在 1 s 和 2 s 能量波段中，每个能级最多可容纳两个电子（向上旋转和向下旋转），因此该波段最多可容纳 2 N 个电子。 在 2 p 能量波段中，每个能级最多可容纳六个电子，因此该波段最多可容纳 6 N 个电子（图\(\PageIndex{3}\)）。

    该图显示了三个阴影矩形，一个在另一个之上，由间隙隔开。 最低的标记为 1s，中间的标记为 2s，顶部的标记为 2p。1s 和 2s 的高度相同，2p 更高。 都具有相同的宽度。 矩形的左边是一个标有能量的箭头，指向上方。
    图\(\PageIndex{3}\)：固体能量结构的简单表示。 电子属于被能量间隙隔开的能量带。

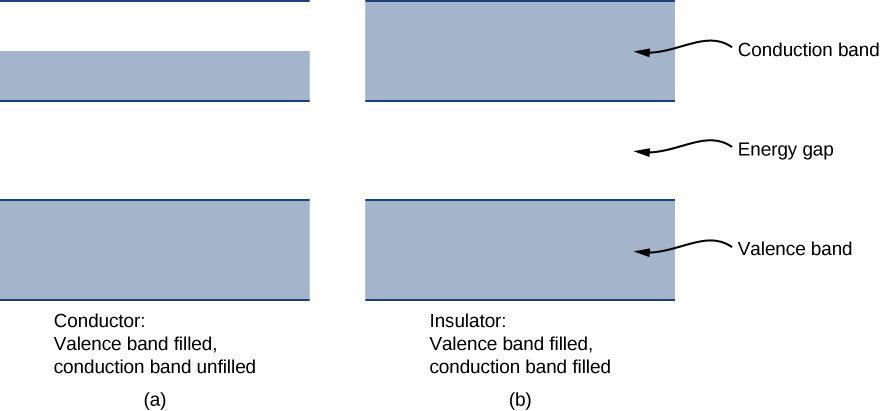
    每个能量带通过能量间隙相互隔开。 导体和绝缘体的电气特性可以用能带和间隙来理解。 填充的最高能量带称为价波段。 能量结构中的下一个可用波段称为传导带。 在导体中，包含电子的最高能带被部分填充，而在绝缘体中，包含电子的最高能带被完全填充。 导体和绝缘体之间的区别如图所示\(\PageIndex{4}\)。

    导体与绝缘体的不同之处在于其电子对施加的电场的反应方式。 如果大量电子被磁场引发运动，则该材料就是导体。 就波段模型而言，部分填充的传导带中的电子通过填充传导带中更高的能量状态从电场中获得动能。 相比之下，在绝缘体中，电子属于完全填充的波段。 施加电场时，由于排除原理，电子无法进行这样的转变（从电场获取动能）。 因此，该材料不传导电能。

    两个图的底部有一个标有价带的矩形，中间有一个空格标有能隙，顶部有一个标记传导带的矩形。 在图 a 中，标有 “导体：帷幔带已填充，传导带未填充”，底部矩形有阴影，上面的矩形仅在下半部分有阴影。 在标有 “绝缘体：帷幔带填充，传导带填充” 的图 b 中，两个矩形都是完全阴影的。
    图\(\PageIndex{4}\)：导体和绝缘体的比较。 最高的能带部分填充在导体中，但完全填充在绝缘体中。
    模拟

    访问这个模拟，了解原子晶体中能带的起源，以及能带的结构如何决定材料如何传导电能。 探索波段结构如何形成由多口井组成的格子。

    半导体具有与绝缘体相似的能量结构，唯一的不同是它在最低的完全填充带和下一个可用的未填充波段之间的能量间隙相对较小。 这种材料构成了现代电子产品的基础。 在\(T = 0 \, K\)，半导体和绝缘体都有完全填充的波段。 唯一的区别在于填充的最高能量带（价带）和下一个较高的空带（传导带）之间的能量隙（或带隙）E g 的大小。 在半导体中，这种间隙足够小，以至于来自价带的大量电子在室温下被热激发到传导带中。 然后，这些电子处于几乎空的波段中，可以对施加的场做出反应。 根据一般经验，半导体的带隙约为 1 eV。 （硅\(\PageIndex{1}\)表。） 大于大约 1 eV 的带隙被视为绝缘体。 相比之下，金刚石（绝缘体）的能隙为几个电子伏特。

    表\(\PageIndex{1}\)：300 KnOTE 时各种材料的能量缺口：除金刚石外，列出的材料均为半导体。
    材质 能量差距\(E_g(eV)\)
    Si \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">1.14
    Ge \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">0.67
    砷化镓溶液 \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">1.43
    GaP \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">2.26
    GasB \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">0.69
    InAs \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">0.35
    inP \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">1.35
    inSB \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">0.16
    C（钻石） \ (e_g (eV)\)” style= “text-align: center;” class= “lt-phys-4545">5.48