Skip to main content
Global

9.7: 半导体和兴奋剂

  1. Last updated
  2. Save as PDF
  • Page ID
    201965

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 描述掺杂导致半导体能量结构 的变化
    • 区分 n 型和 p 型半导体
    • 描述霍尔效应并解释其意义
    • 使用霍尔效应 实验中的信息计算半导体的电荷、漂移速度和电荷载流子数 密度

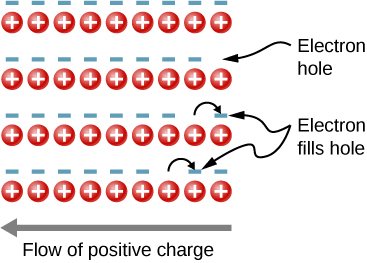
    在上一节中，我们只考虑了由于电子占据 传导带中的状态而对电流的贡献。 但是，将电子从价带移动 到传导带会在价带的能量结构中留下空闲状态或 空洞，附近的电子可以进入 该状态或空洞。 当这些空穴被 其他电子填充时，就会产生新的空洞。 与这种填充 相关的电流可以看作是许多带负电荷 的电子的集体运动或带 正电荷的电子空穴的运动。

    举例来说，以图中的一维格子为例 \(\PageIndex{1}\)。 假设每个晶格原子为电流贡献一个 价电子。 当右边的洞被 填满时，这个洞向左移动。 电流可以解释 为正电荷向左流动。 孔的密度 或每单位体积的孔数由 p 表示。 每个过渡到传导带的电子都会 留下一个洞。 如果传导带最初是空的， 则传导电子密度 p 等于空穴 密度，即\(n = p\)。

    图中显示了四对行。 每对都有最上面一排减号和一排底部带有加号的圆圈。 标有正电荷点向左流动的箭头。 在第二行减号中，缺少最后一个减号。 空白处被标记为电子洞。 在第三行减号中，倒数第二个减号缺失。 从这里到最后一个减号显示一个箭头。 这被标记为电子填充洞。 同样，在第四行减号中，缺少倒数第三个减号。 从这里到倒数第二个减号显示一个箭头。 这也被标记为电子填充孔。
    图\(\PageIndex{1}\)： 晶格中孔的运动。 当电子向右移动时，电子空穴向左 移动。

    如前所述，半导体是一种具有填充 价带、未填充传导带且波段之间 能隙相对较小的材料。 通过将杂质原子置换到 晶格中，可以将多余的电子或空穴 引入材料中，杂质原子是一种价数略有 不同的原子。 这个过程被称为兴奋剂。 例如，假设我们在硅晶体中添加了一个砷原子 （图\(\PageIndex{2a}\)）。

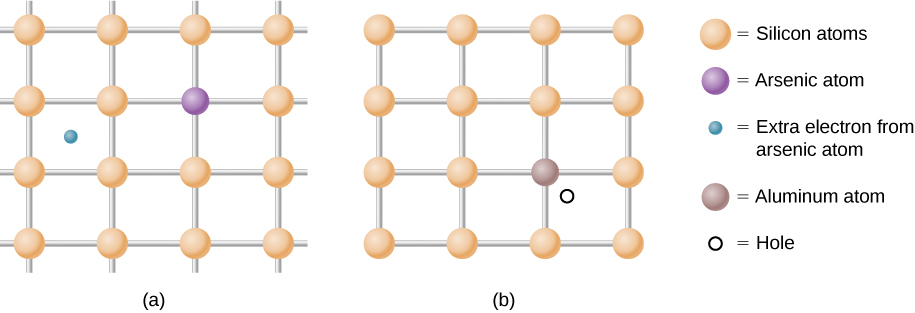
    图 a 显示了一个网格，每个结点上都有标有硅原子的圆圈。 在一个交界处，是一个标有砷原子的另一种颜色的圆圈。 硅原子之间显示了一个小圆圈。 这被标记为来自砷原子的额外电子。 图 b 显示了一个网格，每个结点上都有标有硅原子的圆圈。 在一个交界处，是一个标有铝原子的另一种颜色的圆圈。 硅原子之间显示了一个小圆圈。 这被标记为洞。
    图\(\PageIndex{2}\)：（a）供体杂质和（b） 受体杂质。 将杂质和受体引 入半导体极大地改变了这种材料的电子 特性。

    砷有五个价电子，而硅只有 四个。 因此，这种额外的电子必须进入传导 带，因为价带中没有空间。 留下的砷离子具有净正电荷，可以微弱地结合 去定位的电子。 结合力很弱，因为周围 的原子晶格屏蔽了离子的电场。 因此，额外电子的 结合能仅为0.02 eV左右。 换 句话说，杂质电子的能级在传导 带以下的带隙中乘以0.02 eV， 比间隙的能量值1.14 eV小得多。 在室温下，这种 杂质电子很容易被激发到传导带中， 因此有助于提高电导率（图 \(\PageIndex{3a}\)）。 含有额外电子的杂质被称为 给体杂质，而掺杂的半导体 被称为 n 型半导体，因为 主要的电荷载流子（电子）是负的。

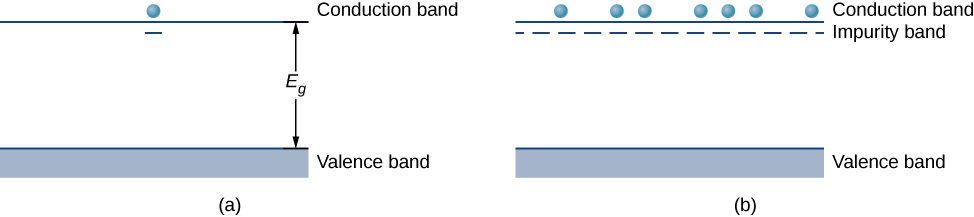
    图 a 显示了底部标有帷幔带的阴影矩形，顶部有一条标有传导带的线。 分离标记为 E 下标 g。传导带顶部有一个电子，其下方有一条短线。 图 b 类似，但许多电子位于传导带以上，带下方的许多短线形成虚线。 虚线被标记为杂质带。
    图\(\PageIndex{3}\)：来自施 体杂质的额外电子被激发到传导带中；(b) 在 n 型半导体中形成 杂质带。

    通过添加更多的给体杂质，我们可以创建一个 杂质带，一个由 半导体掺杂产生的新能量带，如图所示\(\PageIndex{3b}\)。 费米电平现在介于该波段和传导带之间。 在 室温下，许多杂质电子被热激发 到传导带中，并有助于提高电导率。 然后，当杂质带中产生空 位时，传导也可能发生在杂质带中。 请注意，电子能量的变化 对应于这些电荷载流子与半导体的运动（速度或动能） 的变化，但不对应于半导体本身的体积 运动。

    也可以使用杂质原子来完成兴奋，杂质原子 通常比 半导体原子少一个价电子。 例如，具有三个价 电子的铝可以代替硅，如图所示 \(\PageIndex{2b}\)。 这种杂质被称为 受体杂质，而掺杂的半导体 被称为 p 型半导体，因为 电荷的初级载流子（空洞）是正的。 如果将空穴 视为与杂质位点微弱结合的正粒子， 则在价带上方的 带隙中会产生空电子态。 当这种状态由来自价带的 热激发的电子填充时（图 \(\PageIndex{1a}\)），在价带中会产生一个移动洞。 通过添加更多的受体杂质，我们可以创建杂质带， 如图所示\(\PageIndex{1b}\)。

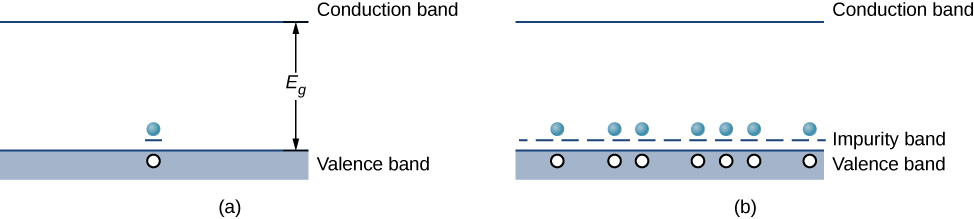
    图 a 显示了底部标有帷幔带的阴影矩形，顶部有一条标有传导带的线。 分离标记为 E 下标 g。价带顶部有一个电子，其下方有一条短线。 电子正下方的价带中有一个洞。 图 b 类似，但有许多电子位于瓦朗带以上，电子下方有许多短线，形成虚线。 虚线被标记为杂质带。 每个电子下方是价带中的一个空洞。
    图\(\PageIndex{4}\)：(a) 来自 传导带的电子被激发到 受体杂质产生的空态；(b) 在 p 型 半导体中形成杂质带。

    掺杂半导体的电流可能是由多数载流子的 运动引起的，其中空穴是由杂质原子 造成的，也可以是少数 载流子造成的，其中空穴纯粹是由电子在能量中的热 激发造成的间隙。 在 n 型半导体中，大多数载流子是由杂质 原子产生的自由电子，少数载流子是从价到 传导带的热激发产生的自由电子。 在 p 型半导体中，大多数 载流子是由杂质原子产生的自由空洞，少数 载流子是由于电子在间隙中的 热激发而填充态所留下的自由空洞。 总的来说，多数航空公司的 数量远远超过少数航空公司。 下一节将使用多数和少数载波的 概念来解释二极管和 晶体管的工作原理。

    霍尔效应

    在研究 p 型和 n 型兴奋剂时， 自然会问：“电子洞” 真的像粒子一样起作用吗？ 霍尔效应 证明了掺杂的 p 型半导体中 存在空洞。 霍尔效应是由于导体在外部 磁场中的运动而产生的电位 差。 霍尔效应的示意图如图所示 \(\PageIndex{5a}\)。

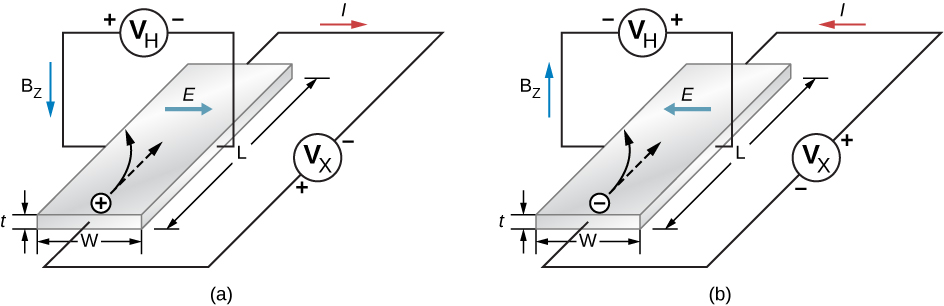
    图 a 显示了长度为 L、宽 W 和厚度 t 的板。电压源 VX 在其长度上相连。 回路中的电流，I 是顺时针方向。 电压源 VH 连接在板的宽度上。 回路中的电流 BZ 是逆时针的。 板上的箭头标有 E。它指向右边。 图 b 与图 a 类似，不同之处在于 VX 和 VH 的极性是相反的，I、BZ 和 E 的方向也相反。
    图\(\PageIndex{5}\)：霍尔效应。 (a) 带正电荷的电子空穴由指向下方的 均匀磁场向左吸引。 右边会 产生一个电场。 (b) 负电荷电子被指向 上方的磁场向左吸引。 左边会 产生一个电场。

    半导体条浸泡在均匀的磁场中 （指向纸张）。 当电子空穴在半导体中从左 向右移动时，洛伦兹力将 这些电荷推向条带的上端。 （回想一下，带正电荷的承运人的 运动是由 右手规则决定的。） 正电荷继续聚集在条带的上 边缘，直到与条带上下边缘之间的向下 电场相关的力 (\(F_E = E_q\)) 刚刚平衡向上的磁力 (\ (F_B = qvB\))。 将这些力设置为彼此相等，我们有\ (E = vB\)。 因此，在条带上产生的电压为

    \[V_H = vBw, \nonumber \]

    其中\(V_H\)是霍尔电压；\(v\)是空穴的 漂移速度，或以部分随机方式移动的粒子的 平均速度；B 是 磁场强度；w 是条带的宽度。 请注意，霍尔电压横向于 最初通过材料产生电流的电压。 通过测量 该电压（或电位差）的符号，证实了带材顶部有孔的 集合。 霍尔电压 的大小产生了 大多数载流子的漂移速度 (v)。

    还可以从霍尔 电压中提取其他信息。 请注意，电子电流密度（半导体条每单位横截面积的 电流量） 为

    \[j = nqv, \label{eq3} \]

    其中 q 是电荷的大小，n 是 每单位体积的电荷载流子数量，v 是 漂移速度。 电流密度很容易通过 将总电流除以 条带的横截面积来确定，q 是空穴的电 荷（单个电子电荷的大小），u 由 方程\ ref {eq3} 确定。 因此，上述电子电 流密度的表达式给出了每单位 体积的电荷载流子数量 n。 可以对 n 型材料中带 负电荷的载流子进行类似的分析（见 图\(\PageIndex{5}\)）。