Skip to main content
Global

9.4: 结晶固体中的粘合

  1. Last updated
  2. Save as PDF
  • Page ID
    201966

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 描述常见固体的包装结构
    • 解释固体和分子中键合的区别
    • 确定给定晶体特性的平衡分离距离
    • 在给定晶体特性下确定盐的解离能

    从本节开始，我们将研究结晶固体，结晶固体由以延伸的规则图案排列的原子组成，称为晶格。 没有或无法形成晶体的固体被归类为无定形固体。 尽管非晶固体（如玻璃）具有各种有趣的技术应用，但本章的重点将放在结晶固体上。

    原子将自身排列在晶格中形成晶体，因为它们的组成电子和原子核之间存在净吸引力。 由原子键合形成的晶体属于三类之一，按其键合分类：离子、共价和金属。 分子也可以结合在一起形成晶体；此处未讨论的这些键被归类为分子。 二十世纪初，固体的原子模型是推测性的。 我们现在有固体中有原子的直接证据（图\(\PageIndex{1}\)）。

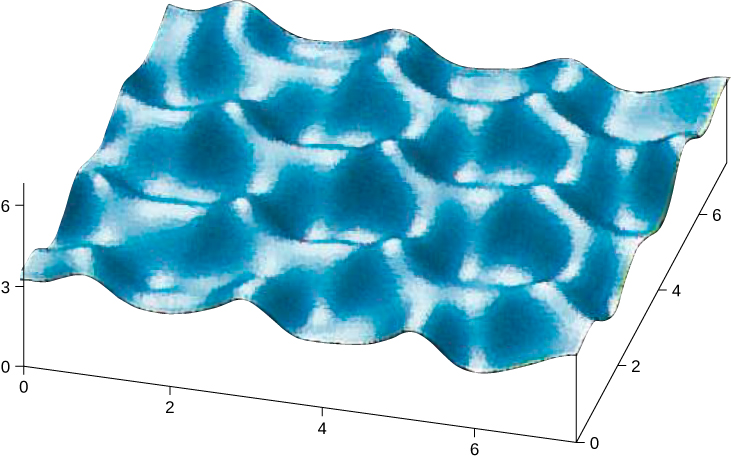
    图中显示了具有峰值和低谷的三维波浪结构。
    图\(\PageIndex{1}\)：用扫描隧道显微镜拍摄的石墨表面的图像。 峰代表原子，它们以六边形排列。 比例以盎格斯特罗姆为单位。

    固体中的离子键合

    许多固体是通过离子键形成的。 一个典型的例子是氯化钠晶体，正如我们前面讨论的那样。 电子从钠原子转移到相邻的氯原子，因为钠中的价电子是松散结合的，氯具有很大的电子亲和力。 带正电荷的钠离子和带负电荷的氯（氯化物）离子组织成延伸的规则原子阵列（图\(\PageIndex{2}\)）。

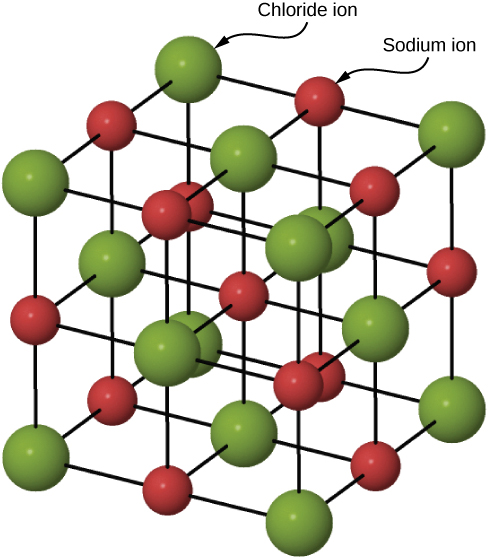
    图中显示了晶格结构，交替放置标有钠离子的红色小球体和标有氯离子的较大绿色球体。
    图\(\PageIndex{2}\)：氯化钠晶体的结构。 钠离子和氯离子以面心立方体 (FCC) 结构排列。

    钠离子和氯离子的电荷分布是球形对称的，氯离子大约是钠离子直径的两倍。 这些离子的最低能量排列称为面心立方体（FCC）结构。 在这种结构中，每个离子最接近其他物种的六个离子。 单位单元是一个立方体——原子占据立方体每个 “面” 的中心和角落。 写下了这六个\(Na^+\)离子的场所产生的\(Cl^-\)离子的诱人势能

    \[U_1 = -6\frac{e^2}{4\pi \epsilon_0 r} \nonumber \]

    其中，减号表示有吸引力的潜力（我们可以识别\(k = 1/4 \pi \epsilon_0\)）。 在远处\(\sqrt{2r}\)是它最接近的邻居：十二个具有相同电荷的\(Na^+\)离子。 与这些离子相关的总排斥势能为

    \[U_2 = 12\frac{e^2}{4\pi \epsilon_0\sqrt{2}r}. \nonumber \]

    接下来最接近的是距离\(Cl^-\)离子 3√r3r 的八个\(Na^+\)离子。 这八个\(Na^+\)离子场中离子的势能为

    \[U_3 = -8\frac{e^2}{4\pi \epsilon_0 \sqrt{3}r}. \nonumber \]

    以同样的方式使用\(Cl^-\)和\(Na^+\)离子的交替集合，我们发现单\(Na^+\)离\(U_A\)子的净有吸引力的势能可以写成

    \[U_{coul} = - \alpha \frac{e^2}{4\pi \epsilon_0 r} \nonumber \]

    前\(\alpha\)面介绍的马德隆常数在哪里。 从这个分析中，我们可以看出这个常数是无限收敛和

    \[\alpha = 6 - \frac{12}{sqrt{2}} + \frac{8}{\sqrt{3}} + . . . \nonumber \]

    远处的离子对这个总和起着重要作用，因此它会缓慢收敛，必须使用许多术语来精确计算 αα。 对于所有 FCC 离子固体，αα 约为 1.75。

    固体中原子的其他可能的包装排列包括简单立方体和体心立方体（BCC）。 图中比较了这三种不同的固体包装结构\(\PageIndex{3}\)。 第一行代表离子的位置，但不代表大小；第二行表示每个结构或晶格的单位细胞；第三行代表离子的位置和大小。 密件抄送结构有八个最近的邻居，Madelung 常数约为 1.76，与 FCC 结构的常数略有不同。 确定特定固体的马德隆常数是一项艰巨的工作，也是当前研究的主题。

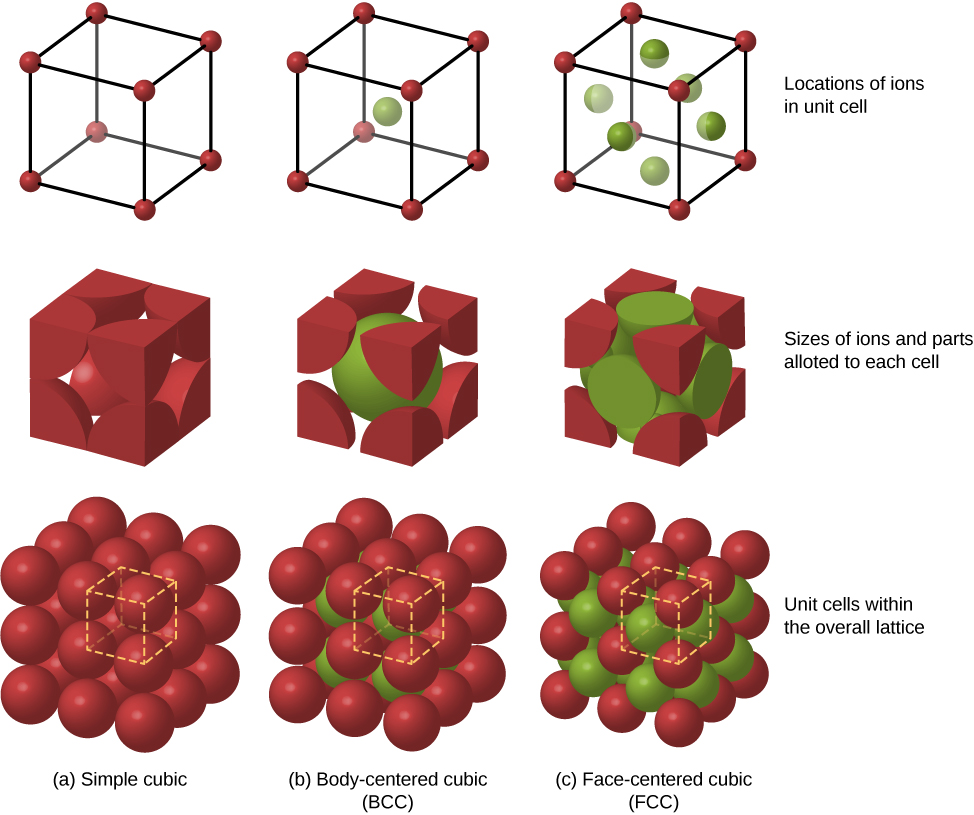
    有九个数字分为三行三列。 这些列标记为：a、简单立方体、b、体心立方体或 BCC，以及 c，面心立方体或 FCC。 在第一行中，第一个图显示了一个八个角落都有红色小球体的立方体。 第二个显示的排列方式相同，中间有一个额外的绿色球体。 第三个立方体的角落有八个红色球体和六个绿色球体，立方体的每个表面各有一个。 该行标有单位细胞中离子的位置。 第二行有三个立方体，与第一行类似，但球体更大，表面被切断。 该行标有分配给每个细胞的离子和部分的大小。 第三行有与前两行相同的三个立方体，但立方体周围还有额外的格子单元。 该行被标记为整个格子内的单位单元。
    图\(\PageIndex{3}\)：从左到右的固体包装结构：(a) 简单立方体，(b) 体心立方体 (BCC)，以及 (c) 面心立方体 (FCC)。 每种晶体结构都将系统的能量降至最低。

    钠离子的能量并不完全来自电荷相反的离子之间的吸引力。 如果购买的离子距离太近，则离子的核心电子的波函数会重叠，并且由于排除原理，电子会被击退。 因此，\(Na^+\)离子的总势能是有吸引力的库仑电位 (\(U_{coul}\)) 和与排除原理 () 相关的排斥电位 (\(U_{ex}\)) 之和。 计算这种排斥潜力需要强大的计算机。 然而，幸运的是，这种能量可以通过一个包含可调整参数的简单公式来准确描述：

    \[U_{ex} = \frac{A}{r^n} \nonumber \]

    其中选择参数 A 和 n 以提供与实验数据一致的预测。 对于本章末尾的问题，参数 n 被称为排斥常数。 因此，\(Na^+\)离子的总势能为

    \[U = -\alpha\frac{e^2}{4\pi \epsilon_0 r} + \frac{A}{r^n}. \nonumber \]

    在平衡状态下，离子上没有净力，因此相邻\(Cl^-\)离子\(Na^+\)和离子之间的距离必须是 U\(r_0\) 为最小值的值。 设置\(\frac{dU}{dr} = 0\)，我们有

    \[0 = \frac{\alpha e^2}{4\pi \epsilon_0 r_0^2} - \frac{nA}{r_0^{n+1}}. \nonumber \]

    因此，

    \[A = \frac{\alpha e^2 r_0^{n-1}}{4\pi \epsilon_0 n}. \nonumber \]

    将这个表达式插入总势能的表达式中，我们有

    \[U = - \frac{\alpha e^2}{4\pi \epsilon_0 r_0} \left[\frac{r_0}{r} - \frac{1}{n}\left(\frac{r_0}{r}\right)^n \right]. \nonumber \]

    请注意，总势能现在只有一个可调参数 n。 参数 A 已被涉及 r0r0（平衡分离距离）的函数所取代，该函数可以通过衍射实验来测量（您在上一章中学过衍射）。 总势能如图 f\(\PageIndex{4}\) or 所示\(n = 0\)，即 NaCl n 的近似值。

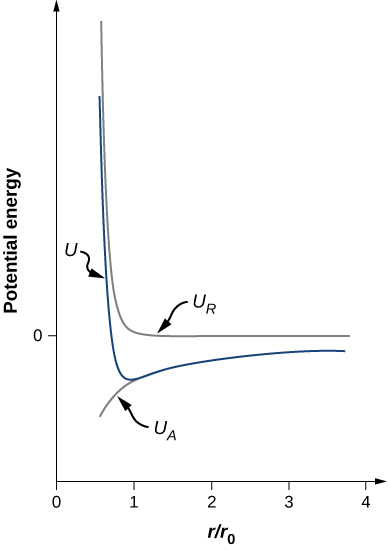
    势能与 r 的对比图 by r 下标 0。 图表上有三条曲线。 标有 U 下标 R 的曲线在一条几乎垂直的线上下降到 y 值为 0，x 值大致为 1。 在这里，它以水平线向右转动并延伸。 标有 U 的曲线同样会向下移动，直到它达到低于零的 y 值。 从这里开始，它稍微上升并均匀到低于零的 y 值。 标有 U 下标 A 的第三条曲线沿着曲线 U 的第二个分支。它与 U 分离，x 值大致为 1，这是曲线 U 的最低点。从这里开始，UA 向右移动。
    图\(\PageIndex{4}\)：NaCl 晶体中钠离子的势能\(n = 8\)。 当能量最小化时，就会出现平衡键长度。

    只要 U 的曲线具有相同的大致形状：U 接近无穷大\(r \rightarrow 0\)，U 接近零\(r \rightarrow \infty\)。\(n > 1\) 势能的最小值由下式给出

    \[U_{min} (r = r_0) = -\alpha \frac{fe^2}{r_0}\left( 1 - \frac{1}{n}\right). \nonumber \]

    因此，将晶体分离成离子所需的每对离子能量为

    \[U_{diss} = \alpha \frac{ke^2}{r_0}\left(1 - \frac{1}{n}\right). \nonumber \]

    这是固体的解离能。 解离能也可以用来描述将一摩尔固体分解成其组成离子所需的总能量，通常以 kj/mole 表示。 解离能量可以使用蒸发的潜热通过实验来确定。 下表给出了示例值。

    表\(\PageIndex{1}\)：碱金属卤化物的晶格能
    \(F^-\) \(Cl^-\) \(Br^-\) \(I^-\)
    \(Li^+\) \ (F^-\)” style= “text-align: center;” class= “lt-phys-4543">1036 \ (Cl^-\)” style= “text-align: center;” class= “lt-phys-4543">853 \ (Br^-\)” style= “text-align: center;” class= “lt-phys-4543">807 \ (I^-\)” style= “text-align: center;” class= “lt-phys-4543">757
    \(Na^+\) \ (F^-\)” style= “text-align: center;” class= “lt-phys-4543">923 \ (Cl^-\)” style= “text-align: center;” class= “lt-phys-4543">787 \ (Br^-\)” style= “text-align: center;” class= “lt-phys-4543">747 \ (I^-\)” style= “text-align: center;” class= “lt-phys-4543">704
    \(K^+\) \ (F^-\)” style= “text-align: center;” class= “lt-phys-4543">821 \ (Cl^-\)” style= “text-align: center;” class= “lt-phys-4543">715 \ (Br^-\)” style= “text-align: center;” class= “lt-phys-4543">682 \ (I^-\)” style= “text-align: center;” class= “lt-phys-4543">649
    \(Rb^+\) \ (F^-\)” style= “text-align: center;” class= “lt-phys-4543">785 \ (Cl^-\)” style= “text-align: center;” class= “lt-phys-4543">689 \ (Br^-\)” style= “text-align: center;” class= “lt-phys-4543">660 \ (I^-\)” style= “text-align: center;” class= “lt-phys-4543">630
    \(Cs^+\) \ (F^-\)” style= “text-align: center;” class= “lt-phys-4543">740 \ (Cl^-\)” style= “text-align: center;” class= “lt-phys-4543">659 \ (Br^-\)” style= “text-align: center;” class= “lt-phys-4543">631 \ (I^-\)” style= “text-align: center;” class= “lt-phys-4543">604

    因此，我们可以从晶体结构中确定 Madelung 常数，从晶格能量中确定 n。 对于 NaCl，我们有\(r_0 = 2.81 A\)\(n \approx 8\)、和\(U_{diss} = 7.84 \, eV/ion \, pair\)。 这种解离能量相对较大。 例如，可见光谱中能量最高的光子的能量约为

    \[hf = (4.14 \times 10^{-15} eV \cdot s)(7.5 \times 10^{14} Hz) = 3.1 \, eV. \nonumber \]

    由于晶体中的离子结合非常紧密，因此离子晶体具有以下一般特征：

    1. 它们相当坚硬且稳定。
    2. 它们在相对较高的温度（1000 到 2000 K）下蒸发。
    3. 它们对可见辐射是透明的，因为光谱可见部分的光子的能量不足以将电子从基态激发到激发态。
    4. 它们是较差的电导体，因为它们实际上不含自由电子。
    5. 它们通常溶于水，因为水分子具有很大的偶极矩，其电场强度足以破坏离子之间的静电键。
    示例\(\PageIndex{1}\): The Dissociation Energy of Salt

    测定 kj/mol 中氯化钠 (NaCl) 的解离能。 （提示：NaCl 的排斥常数 n 约为 8。）

    策略

    氯化钠晶体的平衡分离为 0.282 nm。 （将该值与 0.236 nm 进行比较，得到 NaCl 的游离双原子单位。） 解离能量取决于裂化裂化结构的分离距离、排斥常数和马德隆常数。 分离距离依次取决于摩尔质量和测得的密度。 我们可以确定分离距离，然后使用该值来确定一摩尔固体的解离能。

    解决方案

    钠和氯的原子质量分别为23.0 u和58.4 u，因此氯化钠的摩尔质量为58.4 g/mol。 氯化钠的密度为\(2.16 \, g/cm^3\)。 这些数量之间的关系是

    \[\rho = \frac{M}{V} = \frac{M}{2N_A r_0^3}, \nonumber \]

    其中 M 是一摩尔盐的质量，NANA 是 Avogadro 的数字，r0r0 是平衡分离距离。 需要因子 2，因为钠离子和氯离子都代表立方体积\(r_0^3\)。 求解距离，我们得到

    \[r_0^3 = \frac{M}{2N_A \rho} = \frac{58.4 \, g/mol}{2(6.03 \times 10^{23})(2.160 \, g/cm^3)} = 2.23 \times 10^{-23} \, cm^3, \nonumber \]或者

    \[r_0 = 2.80 \times 10^{-8} cm = 0.280 \, nm. \nonumber \]

    一个离子对 (\(Na^+ Cl^-\)) 的势能为

    \[U = -\alpha \frac{ke^2}{r_0} \left(1 - \frac{1}{n}\right), \nonumber \]

    其中\(\alpha\)是 Madelung 常数，\(r_0\)是平衡间隔距离，n 是排斥常数。 NaCl 是 FCC，所以 Madelung 常数是\(\alpha = 1.7476\)。 用这些值代替，我们得到

    \[U = -1.75 \frac{1.44 \, eV \cdot nm}{0.280 \, nm} \left(1 - \frac{1}{8}\right) = - 7.88 \frac{eV}{ion \, pair}. \nonumber \]

    因此，一摩尔氯化钠的解离能为

    \[D = \left(\frac{7.88 \, eV}{ion \, pair}\right)\left( \frac{\frac{23.052 \, kcal}{1 \, mol}}{\frac{1 \, eV}{ion \, pair}}\right) = 182 \, kcal/mol = 760 \, kJ/mol. \nonumber \]

    意义

    766 kJ/mol 的解离能的理论值接近公认的实验值 787 kJ/mol。 请注意，如预期的那样，对于较大的密度，离子对之间的平衡分离距离会更小。 这种较小的分离距离会增加离子之间的力，从而增加解离能。 方程末尾的转换利用了转换系数\(1 \, kJ = 0.239 \, kcal\)。

    练习\(\PageIndex{1}\)

    如果解离能量更大，那会更容易还是更难将固体分开？

    回答

    更难

    固体中的共价键合

    晶体也可以通过共价键形成。 例如，共价键负责将金刚石晶体中的碳原子保持在一起。 碳原子的电子结构是\(1s^22s^22p^2\) ——一个 He 核加上四个价电子。 这种电子结构比一个完整的壳还差四个电子，因此，通过在共价键中与其他碳原子共享这四个电子，所有碳原子的壳就会被填满。 金刚石的结构比大多数离子晶体更为复杂（图\(\PageIndex{5}\)）。 每个碳原子都是正四面体的中心，键之间的角度为 110°.110°。 这个角度是碳原子 p 轨道的方向性的直接结果。

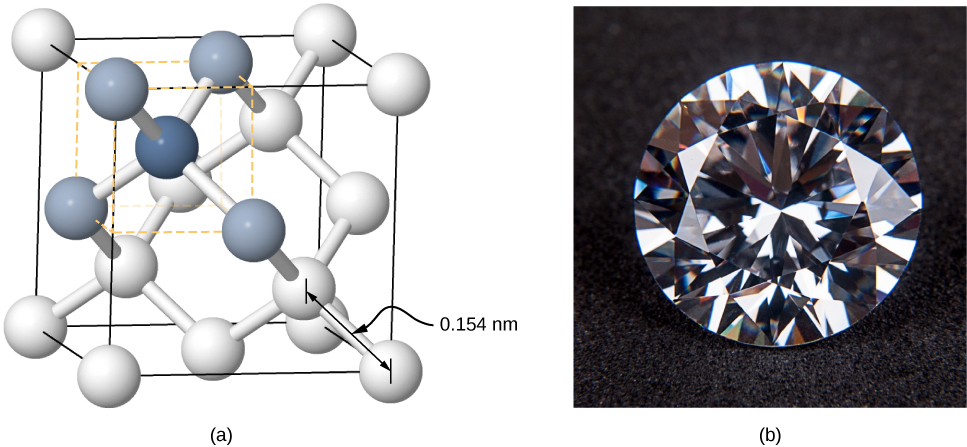
    图 a 显示了晶格。 由虚线形成的立方体标记了格子中的一个区域。 有四个浅蓝色的球体，每个球体在立方体的对角线对角上各一个。 立方体中心有一个深蓝色的球体。 所有球体都通过相同长度的线相互连接。 此长度为 0.154 纳米。 图 b 是一颗钻石的照片。
    图\(\PageIndex{5}\)：金刚石晶体的结构。 (a) 由深蓝色球体表示的单个碳原子与浅蓝色球体所代表的四个碳原子共价结合。 (b) 宝石品质的钻石可以沿着光滑的平面分割，这会产生大量角度，从而使入射光产生完全的内部反射，从而赋予钻石宝石珍贵的光彩。

    共价键合晶体不如离子晶体均匀，但相当坚硬，难以熔化，不溶于水。 例如，钻石具有极高的熔化温度 (4000 K)，并且对可见光是透明的。 相比之下，共价键合锡（也称为α-锡，非金属）相对较软，在600 K时熔化，反射可见光。 共价键合晶体的另外两个重要例子是硅和锗。 这两种固体广泛用于制造二极管、晶体管和集成电路。 我们将在稍后关于半导体的讨论中再次讨论这些材料。

    固体中的金属粘合

    顾名思义，金属粘合是金属晶体形成的原因。 价电子基本上没有原子，能够相对容易地在整个金属晶体中移动。 键合是由于正离子和传导电子之间的吸引力。 金属键比离子键或共价键弱，解离能在此范围内\(1 - 3 \, eV\)。