9.3: 分子光谱
- Page ID
- 201944
在本节结束时,您将能够:
- 使用振动能和旋转能量的概念来描述双原子分子中的能量转变
- 解释双原子分子振动旋转能谱的关键特征
- 估计旋转分子的允许能量
- 根据振动旋转吸收光谱确定双原子分子中原子之间的平衡分离距离
分子能级比原子能级更复杂,因为分子也可以振动和旋转。 与此类运动相关的能量位于不同的范围内,因此可以单独研究。 电子过渡的阶数为 1 eV,振动过渡是有序的\(10^{-2}eV\),旋转过渡是有序的\(10^{-3}eV\)。 对于复杂分子来说,这些能量变化很难表征,因此我们从双原子分子的简单案例开始。
量子旋转
根据经典力学,双原子分子的旋转能量由下式给出
\[E_r = \dfrac{L^2}{2I}, \nonumber \]
其中 I 是惯性矩,L 是角动量。 根据量子力学,旋转角动量是量化的:
\[L = \sqrt{l(l + 1)} \hbar (l = 0,1,2,3,...), \nonumber \]
其中 l 是轨道角量子数。 因此,双原子分子的允许旋转能级为
\[E_r = l(l + 1) \dfrac{\hbar^2}{2I} = l(l + 1) \, E_{0r} \, \, (l = 0,1,2,3,...), \nonumber \]
其中,分子的特征旋转能定义为
\[E_{0r} = \dfrac{\hbar^2}{2I}. \nonumber \]
对于双原子分子,质量减小的惯性矩\(μ\)为
\[I = \mu r_0^2, \nonumber \]
其中\(r_0\)是原子之间的总距离。 因此,旋转水平之间的能量差为
\[\Delta E_r = E_{l+1} - E_l = 2(l + 1) \, E_{0r}. \nonumber \]
要详细研究吸收或发射辐射所带来的旋转能量水平之间的转变(所谓的电偶极子跃变),就需要
\[\Delta l = \pm1. \label{delta l} \]
这条规则被称为选择规则,它限制了从一种量子态到另一种量子态的可能过渡。 方程\ ref {delta l} 是旋转能量转换的选择规则。 它仅适用于具有电偶极矩的双原子分子。 出于这个原因,诸如\(H_2\)和之类的对称分子\(N_2\)不会由于吸收或发射电磁辐射而经历旋转能量转换。
确定氯化氢 ((\(\ce{HCl}\))) 分子的最低三个旋转能级。
策略
氯化氢 (\(\ce{HCl}\)) 是一种双原子分子,平衡分离距离为 0.127 nm。 旋转能级仅取决于惯性 I 的动量和轨道角动量量子数\(l\)(在本例中为\(l = 0\)、1 和 2)。 反过来,惯性动量取决于平衡分离距离(给定)和减少的质量,后者取决于H和Cl原子的质量。
解决方案
首先,我们计算减少的质量。 如果粒子 1 是氢气而粒子 2 是氯化物,我们有
\[\begin{align*} \mu &= \dfrac{m_1m_2}{m_1 + m_2} = \dfrac{(1.0 \, u)(35.4 \, u)}{1.0 \, u + 35.4 \, u} \\[4pt] &= 0.97 \, u = 0.97 \, u \left(\dfrac{931.5 \dfrac{MeV}{c^2}}{1 \, u}\right) \\[4pt] &= 906 \dfrac{MeV}{c^2}. \end{align*} \nonumber \]
因此,相应的静止质量能量是
\[\mu c^2 = 9.06 \times 10^8 \, eV \nonumber \]
这使我们能够计算特征能量:
\[ \begin{align*} E_{0r} &= \dfrac{\hbar^2}{2(\mu r_0^2)} = \dfrac{(\hbar c)^2}{2(\mu c^2)r_0^2} \nonumber \\[4pt] &= \dfrac{(197.3 \, eV \cdot nm)^2}{2(9.06 \times 10^8 eV)(0.127 \, nm)^2} \nonumber \\[4pt] &= 1.33 \times 10^{-3} eV. \nonumber \end{align*} \nonumber \]
(注意这个表达式是如何用剩余质量能量来写的。 这种技术在现代物理计算中很常见。) 旋转能量等级由下式给出
\[E_r = l(l + 1) \dfrac{\hbar^2}{2I} = l(l + 1) E_{0r}, \nonumber \]
哪里\(l\)是轨道量子数。 因此,HCl 分子的三个最低旋转能量水平是
\[\begin{align*} l &= 0:\quad E_r &&= 0 \, eV \, \text{(no rotation)} \\[4pt] l &= 1: \quad E_r &&= 2 \, E_{0r} = 2.66 \times 10^{-3}eV, \\[4pt] l &= 2:\quad E_r &&= 6 \, E_{0r} = 7.99 \times 10^{-3} eV. \end{align*} \nonumber \]
意义
旋转频谱与弱过渡(eV 的 1/1000 到 1/100)有关。 相比之下,处于氢气基态的电子的能量为\(- 13.6 \, eV\)。
双原子分子旋转光谱中吸收线之间的能量分离告诉你什么?
- 回答
-
惯性矩
量子振动
振动能级,即与分子的振动能量相关的能量水平,比旋转能量水平更难估计。 但是,我们可以通过假设双原子分子中的两个原子由弹簧常数 k 的理想弹簧连接来估计这些水平。 这个弹簧系统的潜在能量是
\[U_{osc} = \dfrac{1}{2}k \Delta r^2, \nonumber \]
哪里\(\Delta r\)是分子沿连接原子的直线的 “自然长度” 的变化。 求解薛定方程求解这个电位可以得出
\[E_n = \left(n + \dfrac{1}{2}\right) \hbar \omega \, (n = 0,1,2,. . .), \nonumber \]
其中\(\omega\)是振动的自然角频率,n 是振动量子数。 事实证明,振动能级间隔均匀 (\(\Delta E = \hbar \omega\)) 的预测对较低的能量有好处。
要详细研究吸收或发射辐射引起的振动能量水平之间的转变(特别是所谓的电偶极子转变),就需要
\[\Delta n = \pm 1. \label{delta n} \]
方程\ ref {delta n} 表示振动能量转换的选择规则。 如前所述,该规则仅适用于具有电偶极矩的双原子分子。 对称分子不会经历这样的转变。
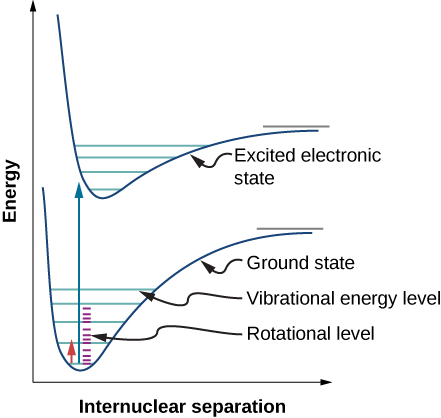
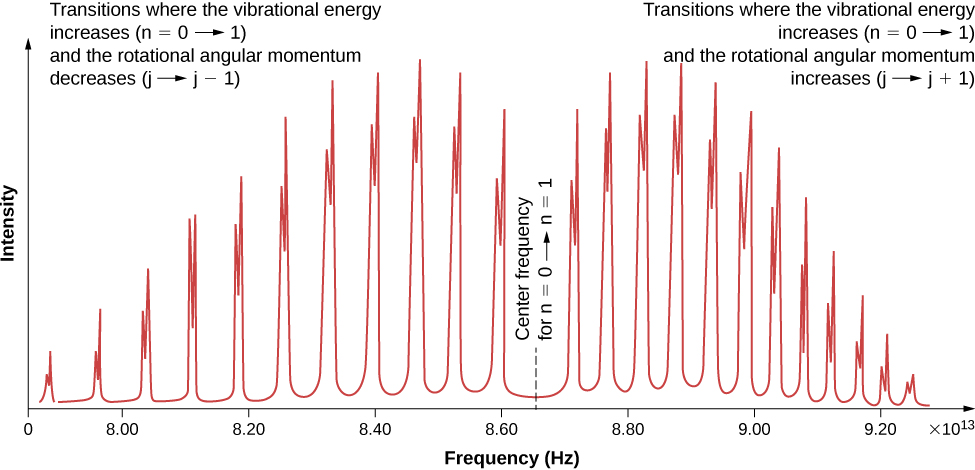
根据选择规则,双原子分子吸收或发射辐射涉及振动和旋转状态的转变。 具体而言,如果振动量子数(n)变化一个单位,则旋转量子数(l)变化一个单位。 图中给出了可能过渡的能量等级图\(\PageIndex{1}\)。 氯化氢 (HCl) 中此类转变的吸收光谱如图 (\ pageIndex {2}\) 所示。 吸收峰值是由于从振动状态过渡\(n = 0\)到\(n = 1\)振动状态造成的。 左侧和右侧峰波段的能量差分别为:
(右波段)
\[ \Delta E_{l \rightarrow l+1} = \hbar \omega + 2(l + 1)E_{0r} = \hbar \omega + 2E_{0r}, \, \hbar \omega + 4E_{0r}, \, \hbar \omega + 6E_{0r}, ... \nonumber \]
(左乐队)
\[ \Delta E_{l \rightarrow l-1} = \hbar \omega - 2l E_{0r} = \hbar \omega - 2E_{0r}, \, \hbar \omega - 4E_{0r}, \, \hbar \omega - 6E_{0r}, .... \nonumber \]
然后可以根据各个峰值之间的能量间距 (\(2E_{0r}\)) 或左右波段之间的间隙 (\(4E_{0r}\)) 来确定惯性矩。 该间隙中心的频率是振动频率。