9.2: 分子键的类型
- Page ID
- 201951
在本节结束时,您将能够:
- 区分不同类型的分子键
- 使用电离能、电子亲和力和库仑力的概念确定分子的解离能
- 用交换对称性描述共价键
- 用杂交的概念解释分子的物理结构
量子力学在解释分子的结构和键合方面非常成功,因此是所有化学的基础。 有时被称为量子化学,它解释了诸如分子为何存在,为什么该\(H_2O\)分子中氢原子之间的结合角恰好为104.5°,以及为什么这些分子在室温下结合在一起形成液态水等基本问题。 从数学上讲,将量子力学应用于分子可能非常困难,因此我们的讨论将仅限于定性的。
当我们先研究分子,然后研究固体时,我们将使用许多不同的科学模型。 在某些情况下,我们将分子或晶体视为一组点核,电子以明确的轨迹在外部旋转,就像玻尔模型一样。 在其他情况下,我们利用量子力学的全部知识使用波函数和电子自旋的概念来研究这些系统。 重要的是要记住,我们使用模型研究现代物理学,不同的模型可用于不同的目的。 我们并不总是使用最强大的模型,因为功能较弱、更易于使用的模型可以胜任。
债券的种类
化学单位由许多不同种类的化学键形成。 当电子从一个原子转移到另一个原子时,就会形成离子键。 当两个或多个原子共享电子时,就会产生共价键。 范德华键是由于电荷极化分子的吸引而产生的,它比离子键或共价键弱得多。 还存在许多其他类型的粘合。 通常,粘合是通过多种机制发生的。 本节的重点是离子键和共价键。
离子键
离子键可能是最容易理解的键合类型。 它解释了盐化合物的形成,例如氯化钠\(\ce{NaCl}\)。 钠原子(符号 Na)的电子排列与霓虹原子加一个 3 s 电子相同。 从钠原子中移除这个电子只需要5.14 eV的电离能。 因此,钠可以很容易地放弃这种电子或将这种电子捐赠给相邻(附近)的原子,从而获得更稳定的电子排列。 氯(符号 Cl)只需要一个电子就能完成其价壳,因此,如果这个电子靠近钠原子,它很容易接受这个电子。 因此,我们说氯具有很大的电子亲和力,这是与可接受的电子相关的能量。 在此过程中,氯原子释放的能量为 3.62 eV。 电子从钠原子转移到氯原子后,钠原子变成正离子,氯原子变成负离子。
这个反应看起来像这样
\[\ce{Na(g) + Cl(g) -> Na^{+}(g) + Cl^{-}(g)} \label{rx1} \]
这种转移所需的总能量由下式给出
\[E_{transfer} = 5.14 \,\text{eV} - 3.62 \,\text{eV} = 1.52 \,\text{eV}. \label{9.1} \]
正钠离子和负氯离子会产生诱人的库仑力。 与该力相关的潜在能量由下式给出
\[U_{coul} = -\dfrac{ke^2}{r_0}, \nonumber \]
其中\(ke^2 = 1.440\, \text{eV-nm}\),\(r_0\)是离子之间的距离。
随着钠离子和氯离子一起移动(“下降潜在能量山”),离子之间的吸引力变得更强。 但是,如果离子距离太近,两个离子中的核心电子波函数就会开始重叠。 由于排斥原理,这种作用将核心电子(因此也是整个分子)提升到更高的能量状态。
\[\ce{ Na^{+}(g) + Cl^{-}(g) -> NaCl(g)} \label{rx2} \]
离子之间的平衡分离距离(或键长度)发生在分子处于最低能量状态时。 对于双原子\(\ce{NaCl}\),此距离为 0.236 nm。 该图\(\PageIndex{1}\)显示了的\(\ce{NaCl}\)总能量与离子之间分离距离的关系。
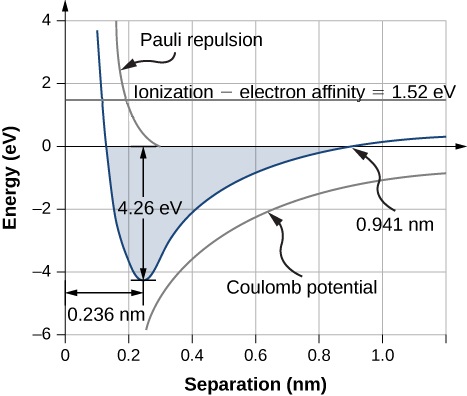
由中性和\(\ce{Na}\)\(\ce{Cl}\)原子形成单一盐单位所需的总能量是与电子转移(方程\ ref {rx1})和离子组合(方程\ ref {rx2})相关的能量之和:
\[U_{form} = E_{transfer} + U_{coul} + U_{ex}, \nonumber \]
由于保利的排除原理,与核心电子之间的排斥相关的能量在哪里\(U_{ex}\)。 的值\(U_{form}\)必须为负才能使键自发形成(否则,分离的物种的能量会降低)。 解离能被定义为将单位分离成其组成离子所需的能量,写成
\[U_{diss} = -U_{form} \nonumber \]
每个双原子公式单元都有自己特有的解离能和平衡分离长度。 示例值在表中给出\(\PageIndex{1}\)。
债券可以对称或不对称地被破坏。 前者被称为均解,是通常(均解)键解离能的基础。 对于盐配方单位 (\(\ce{NaCl}\)),相关的均解反应为
\[\ce{NaCl(g) -> Na (g) + Cl(g)} \label{homo} \]
键的不对称分离称为杂解(即异解键解离能)。 的相关杂解反应\(\ce{ NaCl}\)将是
\[\ce{NaCl(g) -> Na^{+} (g) + Cl^{-}(g)} \label{hetero} \]
均解键和异解键解离能的差异仅由方程\ ref {9.1}\(E_{transfer}\) 给出。
| 分子 | 解离能 (eV) | 平衡分离 (nm)(键合长度) |
|---|---|---|
| 氯化钠 | 4.26 | 0.236 |
| NaF | 4.99 | 0.193 |
| naBR | 3.8 | 0.250 |
| NaI | 3.1 | 0.271 |
| NaH | 2.08 | 0.189 |
| LiCL | 4.86 | 0.202 |
| LiH | 2.47 | 0.239 |
| LiI | 3.67 | 0.238 |
| KCl | 4.43 | 0.267 |
| kBr | 3.97 | 0.282 |
| rbF | 5.12 | 0.227 |
| rbcL | 4.64 | 0.279 |
| CSi | 3.57 | 0.337 |
| H-H | 4.5 | 0.075 |
| N-N | 9.8 | 0.11 |
| O-O | 5.2 | 0.12 |
| F-F | 1.6 | 0.14 |
| Cl-Cl | 2.5 | 0.20 |
盐配方单位 (NaCl) 的解离能是多少?
策略
氯化钠 (\(\ce{NaCl}\)) 是由离子键形成的盐。 与该键相关的能量变化取决于三个主要过程:
- 钠的电离和氯原子接受来自钠原子的电子;以及
- 由此产生的离子的库仑吸引力(\(\ce{Na^{+}}\)和\(\ce{Cl^{-}}\))。
- 如果离子距离太近,则由于排除原理(0.32 eV),它们会被击退。
平衡间隔距离为\(r_0 = 0.236 \text{nm}\)。
解决方案
与电子从 Na 转移到 Cl 相关的能量变化为 1.52 eV(方程\ ref {9.1})。 在平衡分离时,原子是分\(r_0 = 0.236 \text{nm}\)开的。 原子的静电势能为
\[\begin{align*} U_{could} &= -\dfrac{ke^2}{r_0} \\[5pt] &= - \dfrac{1.44 \, \text{eV} \cdot nm}{0.236 \,nm} \\[5pt] &= - 6.10 \, \text{eV} . \end{align*} \nonumber \]
与形成 NaCl 公式单位相关的总能量差为
\[\begin{align*}E_{form} &= E_{transfer} + U_{coul} + U_{ex} \\[5pt] &= 1.52 \, \text{eV} + (−6.10 eV) + 0.32\, \text{eV} \\[5pt] &= -4.26 eV \end{align*} \nonumber \]
因此,的均解解离能\(\ce{NaCl}\)为 4.26 eV。
意义
通过离子键形成 NaCl 配方单元在能量上是有利的。 解离能量或将 NaCl 单元分离成\(Na\)和\(Cl\)原子所需的能量为 4.26 eV,与图一致\(\PageIndex{1}\)。
为什么示例中与排除原则相关的潜在能量是积极的\(\PageIndex{1}\)?
- 回答
-
它对应于离子中核心电子之间的排斥力。
这种反应发生在多\(\ce{Na}\)\(\ce{Cl}\)远的能量上是有利的?
\[\ce{Na(g) + Cl(g) -> Na^{+}(g) + Cl^{-}(g)} \nonumber \]
- 回答
-
当电势能 (\(U_{coul}\)) 和 Pauli 排斥能 () 等式计算电子传递的能量 (\(U_{ex}\)) 时,就会发生这种情况,如图所示,电子转移的能量为 0.941 nm\(\PageIndex{1}\)。\(E_{transfer}\) 请注意,\(U_{ex} \approx 0\)在这个距离处。
对于离子 NaCl 晶体中的钠离子,库仑势能的表达\(U_{could}\)必须通过一种称为 Madelung 常数的因子进行修改。 该因子考虑了钠离子与附近所有氯离子和钠离子的相互作用。 氯化钠晶体的马德隆常数约为 1.75。 该值意味着\(Na^+\)和离子之间的平衡分\(Cl^-\)离距离为 0.280 nm,略大于双原子 NaCl。 稍后我们将再次讨论这个问题。
共价债券
在离子键中,电子从一个原子转移到另一个原子。 但是,在共价键中,电子在两个原子之间共享。 离子键机制无法解释\(H_2\)\(O_2\)、和 CO 等分子的存在,因为不存在任何分离距离,负势吸引能量大于产生离子所需的能量。 准确理解这些分子是如何共价结合的,取决于对量子力学的更深入理解,这超出了本书的范围,但我们将在下一节中定性地描述这些机制。
共价键可以用\(\ce{H_2^{+}}\)分子的简单例子来理解,分子由两个质子的电场中的一个电子组成。 该系统可以通过双方阱中的电子建模(图\(\PageIndex{2}\))。 在每个井中发现电子的可能性相同,因此波函数要么是对称的,要么是反对称的,要么是相反的。
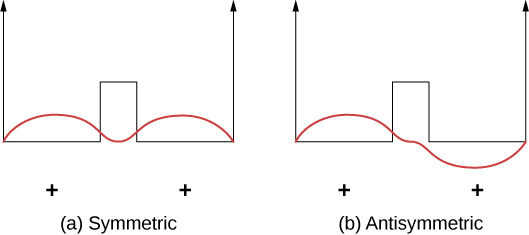
现在想象一下,两口井相隔很远的距离。 在基态下,波函数存在于两种可能的状态之一:要么是两个井中的单个正峰(类似正弦波的 “驼峰”)(对称情况),要么是一个井中有正峰而另一个井中有负峰(反对称情况)。 这些州具有相同的能量。 但是,当井聚集在一起时,对称波函数变成基态,反对称态成为第一个激发态,换句话说,电子的能级会被分裂。 注意,空间对称状态变成了能量有利(能量较低)的状态。
同样的分析适用于与两个氢原子结合的电子。 在这里,基态波函数的形状具有\(e^{(-|x|/a_0)}\)形式\(e^{-r/a_0}\)或一维。 能量上有利的空间对称状态意味着质子中间的电荷密度很高,电子很可能会将带正电荷的质子聚集在一起。
如果将第二个电子添加到该系统中以形成\(H_2\)分子,则波函数必须描述两个粒子,包括它们的空间关系和相对自旋。 这种波函数还必须尊重电子的不可区分性。 (“如果你看见了一个电子,你就全部看见了。”) 特别是,切换或交换电子不应产生可观察到的效应,这种特性称为交换对称性。 交换对称性可以是对称的,波函数不会发生变化,也可以是反对称的,波函数的符号会发生整体变化,两者都不可观察。
正如我们稍后讨论的那样,两个电子的总波函数在交换时必须是反对称的。 例如,与氢分子结合的两个电子可以处于空间对称状态,具有反平行自旋 (↑↓) 或具有平行自旋的空间反对称状态 (↑↑)。 具有反平行自旋的状态在能量上是有利的,因此用于共价键。 但是,如果质子之间的距离太近,质子之间的排斥就变得很重要。 (在其他分子中,这种效应由排除原理提供。) 结果,\(H_2\)达到约0.074 nm的平衡分离,结合能为4.52 eV。
访问此 PBS Learning Media 教程和交互式模拟,探索作用于\(H_2\)分子中原子粒子和共价键的吸引力和排斥力。
量子力学排除了许多类型的分子。 例如,分子\(H_3\)不会形成,因为如果第三个 H 原子接近双原子氢,则该原子中电子的波函数与其他两个原子中的电子重叠。 如果所有三个电子都处于各自原子的基态,则一对电子共享所有相同的量子数,这是排除原理所禁止的。 相反,其中一个电子被迫进入更高的能量状态。 这个过程的总能量变化为负的三个质子之间不存在分离,也就是说,键合是自发发生的地方。 同样\(He_2\),在正常条件下也不会共价键合,因为这些原子没有价电子可以共享。 当原子聚集在一起时,核心电子的波函数会重叠,并且由于排除原理,电子被迫进入更高的能量状态。 不存在这种分子在能量上有利的分离。
多原子分子中的键合
多原子分子是由两个以上原子组成的分子。 例子包括从简单的水分子到复杂的蛋白质分子。 这些分子的结构通常可以用共价键和杂交来理解。 杂交是原子能量结构的变化,其中混合态(可以写成其他态的线性叠加)参与键合。
为了说明杂交,可以考虑一个简单的水分子中的键合\(H_2O\)。 氧气的电子结构是\(1s^22s^22p^4\)。 1 s 和 2 s 电子位于 “封闭壳” 中,不参与键合。 剩下的四个电子是价电子。 这些电子可以填充六种可能的状态(\(l = 1, m = 0, \pm 1\)加上上下旋转)。 这些态的能量是相同的,因此氧原子可以利用这些态的任意线性组合与氢原子结合。 这些线性组合(你在原子结构一章中学到的)被称为原子轨道,它们用\(p_x\)\(p_y\)、和表示\(p_z\)。 图中给出了这些轨道的电子电荷分布\(\PageIndex{3}\)。
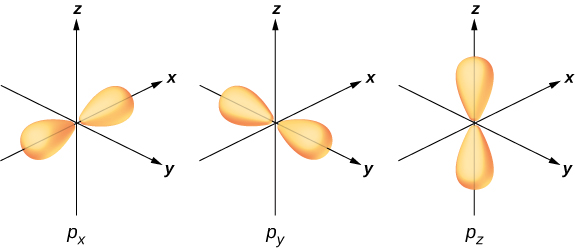
在氢原子存在的情况下\(p_x, p_y\),氧气的电子波函数向氢原子和\(p_z\)轨道的转化就是杂交的一个例子。 在\(p_z\)轨道上发现了两个带有配对自旋的电子 (↑↓)。 在每个\(p_x\)和\(p_y\)轨道中都发现一个电子,自旋未成对。 后者轨道参与与氢原子的结合。 根据图\(\PageIndex{3}\),我们预计 H—O—H 的粘合角度为 90°。 但是,如果我们将原子之间的排斥效应包括在内,则键合角为 104.5°。 同样的论点可以用来理解甲烷 (\(CH_4\)) 和其他分子的四面体形状。


