8.5: 排除原则和元素周期表

Last updated
Save as PDF

Page ID: 202220

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释保利的排除原理对理解原子结构和分子键的重要性
用原子中单个电子的总能量、轨道角动量和自旋来解释元素周期表的结构
描述元素周期表中原子的电子构型

到目前为止，我们只研究了氢气，这是最简单的化学元素。我们发现氢原子中的电子可以完全用五个量子数来表示：

\(n\):主量子数
\(l\): 角动量量子数
\(m\): 角动量投影量子数
\(s\): 自旋量子数
\(m_s\): 自旋投影量子数

要构造中性多电子原子的基态，想象一下从电荷核 Ze（即原子序数 Z 的原子）开始，然后逐个添加 Z 电子。假设每个电子在原子的原子核和所有其他电子产生的球形对称电场中移动。该假设是有效的，因为电子在原子核周围随机分布，产生球形对称的平均电场（和电位）。由于电子之间的相互作用，每个电子的电势 U（r）并不遵循简单的\(-1/r\)形式，但事实证明，我们仍然可以用量子数来标记每个单独的电子态，（\(n,l,m,s,m_s\)）。（所有电子的自旋量子数\(s\)都相同，因此本节将不使用它。）

保利的排除原理在一定程度上解释了原子的结构和化学性质：原子中没有两个电子对所有四个量子数具有相同的值（\(n,l,m,m_s\)）。这个原理与电子的两个特性有关：所有电子都是相同的（“当你看见一个电子时，你就全部看见了”），它们有半积分自旋（\(s = 1/2\)）。表中给出了原子中电子的量子数样本集\(\PageIndex{1}\)。与保利的排除原则一致，表中没有两行具有完全相同的量子数集。

表\(\PageIndex{1}\)：原子的电子态由于保利的排除原理，原子中没有两个电子具有相同的四个量子数集。
\(n\)	\(l\)	\(m\)	\(m_s\)	子壳符号	电子数量：子壳	电子数量：外壳
\ (n\)” style= “垂直对齐:middle;” >1	\ (l\)” style= “垂直对齐:middle;” >0	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >½	1 秒	2	2
\ (n\)” style= “垂直对齐:middle;” >1	\ (l\)” style= “垂直对齐:middle;” >0	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >—½	1 秒	2	2
\ (n\)” style= “垂直对齐:middle;” >2	\ (l\)” style= “垂直对齐:middle;” >0	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >½	2 s	2	8
\ (n\)” style= “垂直对齐:middle;” >2	\ (l\)” style= “垂直对齐:middle;” >0	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >—½	2 s	2
\ (n\)” style= “垂直对齐:middle;” >2	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >—1	\ (m_s\)” style= “vertical-align: middle;” >½	2 p	6
\ (n\)” style= “垂直对齐:middle;” >2	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >—1	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >2	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >½
\ (n\)” style= “垂直对齐:middle;” >2	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >2	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >1	\ (m_s\)” style= “vertical-align: middle;” >½
\ (n\)” style= “垂直对齐:middle;” >2	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >1	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >0	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >½	3 s	2	18
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >0	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >—½	3 s	2
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >—1	\ (m_s\)” style= “vertical-align: middle;” >½	3 p	6
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >—1	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >1	\ (m_s\)” style= “vertical-align: middle;” >½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >1	\ (m\)” style= “垂直对齐:middle;” >1	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >—2	\ (m_s\)” style= “vertical-align: middle;” >½	3 d	10
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >—2	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >—1	\ (m_s\)” style= “vertical-align: middle;” >½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >—1	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >0	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >1	\ (m_s\)” style= “vertical-align: middle;” >½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >1	\ (m_s\)” style= “vertical-align: middle;” >—½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >2	\ (m_s\)” style= “vertical-align: middle;” >½
\ (n\)” style= “垂直对齐:middle;” >3	\ (l\)” style= “垂直对齐:middle;” >2	\ (m\)” style= “垂直对齐:middle;” >2	\ (m_s\)” style= “vertical-align: middle;” >—½

据说具有相同主量子数 n 的电子位于同一个壳中，而那些具有相同值 l 的电子据说占据了同一个子壳。处于氢原子\(n = 1\)状态的电子表示为 1 s，其中第一个数字表示壳 (\(n = 1\))，字母表示子壳（\(s,p,d,f,...\)对应\(l = 0,1,2,3,...\)）。处于该\(n = 1\)状态的两个电子表示为\(1s^2\)，其中上标表示电子的数量。 \(n = 2\)状态为的电子表示\(l = 1\)为 2 p。处于 and\(l = 0\) 状态的两个电子\(n = 2\)以及处于 and\(l = 1\) 状态的三个电子的组合写为\(2s^22p^3\)，依此类推。\(n = 2\) 这种电子态的表示称为原子的电子构型。表中给出了几个原子的电子构型\(\PageIndex{2}\)。原子外壳中的电子被称为价电子。分子中原子之间的化学键可以通过价电子的转移和共享来解释。

表\(\PageIndex{2}\)：原子中电子的电子构型。符号 (↑) 表示外壳中未成对的电子，而符号 (↑↓) 表示外壳中有一对向上自旋和向下旋的电子。
元素	电子配置	自旋校准
H	\(1s^1\)	(↑)
他	\(1s^2\)	(↑↓)
李	\(1s^22s^1\)	(↑)
是	\(1s^22s^2\)	(↑↓)
B	\(1s^22s^22p^1\)	(↑↓) (↑)
C	\(1s^22s^22p^2\)	(↑↓) (↑) (↑)
N	\(1s^22s^22p^3\)	(↑↓) (↑) (↑) (↑)
O	\(1s^22s^22p^4\)	(↑↓) (↑↓) (↑) (↑)
F	\(1s^22s^22p^5\)	(↑↓) (↑↓) (↑↓) (↑)
Ne	\(1s^22s^22p^6\)	(↑↓) (↑↓) (↑↓) (↑↓)
娜	\(1s^22s^22p^63s^1\)	(↑)
镁	\(1s^22s^22p^63s^2\)	(↑↓)
阿尔	\(1s^22s^22p^63s^13p^1\)	(↑↓) (↑)

子壳中的最大电子数取决于角动量量子数 l 的值。对于给定值 l，存在\(2l + 1\)轨道角动量状态。但是，每种状态都可以由两个电子填充（上下旋转，↑↓）。因此，子壳中的最大电子数为

\[N = 2(2l + 1) = 4l + 2. \nonumber \]

在 2 s (\(l = 0\)) 子壳中，最大电子数为 2。在 2 p (\(l = 1\)) 子壳中，最大电子数为 6。因此，\(n = 2\)外壳（包括\(l = 0\)和 1 个子壳）中的最大电子总数为\(2 + 6\)或 8。通常，第 n 个壳中的最大电子数为\(2n^2\)。

示例\(\PageIndex{1}\): Subshells and Totals for \(n = 3\)

外壳中有多少子\(n = 3\)壳？识别每个子壳并计算将填充每个子壳的最大电子数。表明填充原子的最大电子数为\(2n^2\)。

策略

子壳由 l 的值决定；因此，我们首先确定 l 的哪些值是允许的，然后我们应用 “a\(subshell = 2(2l + 1\)) 中可以存在的最大电子数” 方程来计算每个子壳中的电子数量。

解决方案

因为\(n = 3\)，我们知道 l 可以是 0、1 或 2；因此，有三个可能的子壳。在标准表示法中，它们被标记为 3 s、3 p 和 3 d 子壳。我们已经看到，两个电子可以处于 s 态，六个电子可以处于 p 态，但让我们使用方程式 “可以处于 a 状态的最大电子数

subshell\(= 2(2l + 1)\)” 来计算每个中的最大数量：

\(3s\)有\(l = 0\)；因此，\(2(2l + 1) = 2(0 + 1) = 2\)

\(3p\)有\(l = 1\)；因此，\(2(2l + 1) = 2(2 + 1) = 6\)

\(3d\)有\(l = 2\)；因此，\(2(2l + 1) = 2(4 + 1) = 10\)

\(Total = 18\)

（在\(n = 3\)外壳中）。

方程式 “壳中可以存在的最大电子数 =\(2n^2\)” 给出了\(n = 3\)壳中的最大电子数为

最大电子数\(= 2n^2 = 2(3)^2 = 2(9) = 18\)。

意义

因此，三个可能的子壳中的电子总数与公式相同\(2n^2\)。在标准（光谱）表示法中，填充的\(n = 3\)外壳表示为\(3s^23p^63d^{10}\)。贝壳不是用简单的方式填充的。例如，在\(n = 3\)外壳完全填充之前，我们开始在\(n = 4\)外壳中找到电子。

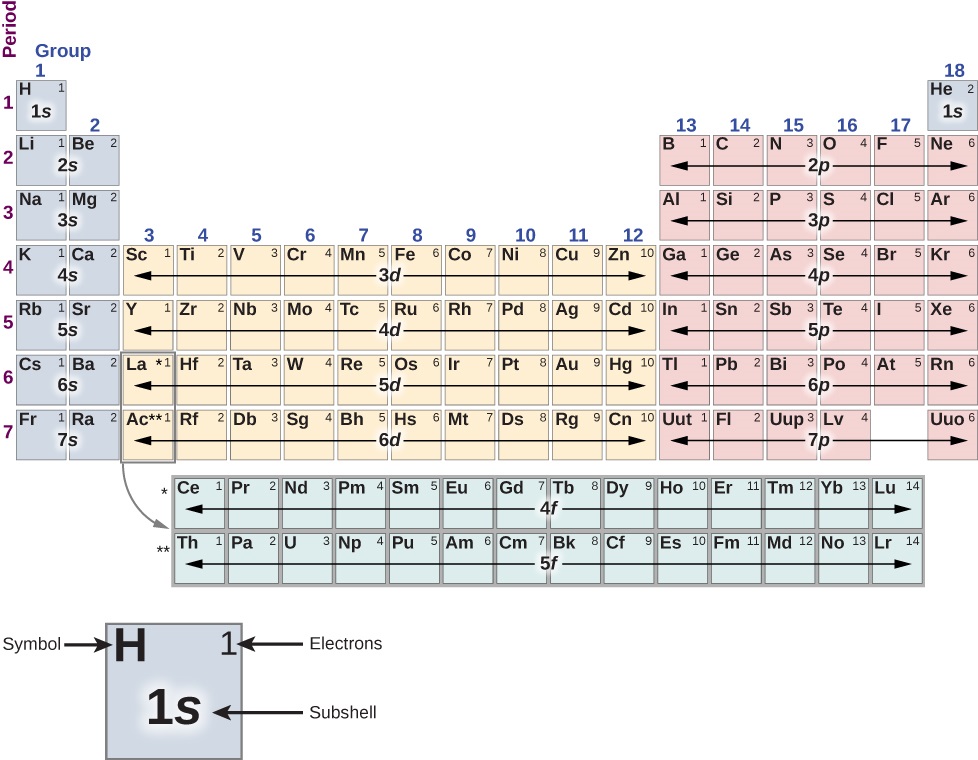
元素周期表（图\(\PageIndex{1}\)）的结构可以用壳和子壳来理解，最终可以用原子中电子的总能量、轨道角动量和自旋来理解。关于元素周期表的详细讨论留给化学课程——我们在这里仅概述其基本特征。在本次讨论中，我们假设原子是电中性的；也就是说，它们具有相同数量的电子和质子。（回想一下，原子核中的质子总数称为原子序数 Z。）

首先，元素周期表按列和行排列。该表按原子序数增加的顺序从左到右、从上到下读取\(Z\)。属于同一柱或化学组的原子具有许多相同的化学特性。例如，Li 和 Na 原子（在第一列中）以类似的方式与其他原子结合。表的第一行对应于原子的 1 s (\(l = 0\)) 壳。

以一个接一个地向原子添加电子的假设程序为例。对于氢气 (H)（左上角），1 s 外壳充满了向上或向下旋转的电子（↑ 或 ↓）。这种孤独的电子很容易与其他原子共享，因此氢具有化学活性。对于氦气（He）（右上角），1 s 外壳充满了向上旋转和向下旋转（↑↓）的电子。这 “填充” 了 1 的外壳，所以氦原子往往不会与其他原子共享电子。据说氦原子具有化学活性、惰性或稀有气体；同样，氦气被认为是惰性气体或稀有气体。

通过加减质子、中子和电子来构建原子。元素、电荷和质量如何变化？访问 PhET 探索：构建 Atom，探索这些问题的答案。

图中显示了元素周期表，显示了贝壳和子壳的结构。 18 列的编号标记为 “组”，7 行编号并标记为 “句点”。组 1 和组 2 使用紫色阴影。第 3 组到第 12 组用黄色阴影。第 13 组到第 18 组采用红色阴影，但时段 1 的第 18 组除外，该组为紫色。句点 6 和 7 的第 3 组方框被勾勒出来，箭头从它们指向另外一个由两行和十四列组成的部分，阴影为绿色。句点 6 组 3 框中有一个星号，该星号也出现在附加部分第一行的左侧。句点 7 组 3 框有两个星号，它们也出现在附加部分第二行的左侧。左边的表格下方是桌子上最左上角的方框的放大图。字母 “H” 位于其左上角，标有 “符号”。数字 1 位于其右上角，标有 “电子”。在其中间，条目 “1 s” 被标记为 “子壳”。盒子是紫色阴影。每个元素在框中都有其符号和电子。子壳以一行中连续部分的组表示。从表的左上角开始，周期 1，组 1 以紫色阴影表示，包含符号 H、电子 1、子壳 1 s。周期 1 中唯一的其他元素框位于最后一列组 18 中，该组以紫色阴影显示，包含 “H e, 1, 1 s”。时段 2，组 1 包含 “L i，1” 第 2 组包含 “B e，2”。时段 2 组 1 和 2 都有子外壳 2 s。跳过组 3 到 12。组 13 包含 “B, 1”。组 14 包含 “C, 2”。组 15 包含 “N, 3”。第 16 组包含 “O，4”。第 17 组包含 “F, 5”。第 18 组包含 “N e，6”。时段 2 组 13 到 18 有子壳 2 p。时段 3，组 1 包含 “N a,1”。第 2 组包含 “M g，2”。这两个有子外壳 3 s。第 3 组至第 12 组在时段 3 中再次被跳过，组 13 包含 “A l，1”。第 14 组包含 “S I，2”。组 15 包含 “P, 3”。组 16 包含 “S, 4”。第 17 组包含 “C l，5”。第 18 组包含 “A r, 6”。这 6 个有子壳 3 p。时期 4，组 1 包含 “K，1”。组 2 包含 “C a, 2”。这两个有子外壳 4 s。组 3 包含 “S, 1”。第 4 组包含 “T i，2”。第 5 组包含 “V, 3”。第 6 组包含 “C r, 4”。第 7 组包含 “M n, 5”。第 8 组包含 “F e，6”。第 9 组包含 “C o，7”。第 10 组包含 “N i，8”。第 11 组包含 “C u，9”。第 12 组包含 “Z n, 10”。这 10 个有子壳 3 d。组 13 包含 “G a，1”。第 14 组包含 “G e，2”。组 15 包含 “A s, 3”。第 16 组包含 “S e，4”。第 17 组包含 “B r，5”。第 18 组包含 “K r，6”。这六个有子壳 4 p。时期 5，组 1 包含 “R b，1”。组 2 包含 “S r, 2”。这 2 个有子外壳 5 s。组 3 包含 “Y, 1”。组 4 包含 “Z r, 2”。第 5 组包含 “N b, 3”。第 6 组包含 “M o，4”。第 7 组包含 “T c，5” R u，6”。第 9 组包含 “R h，7”。第 10 组包含 “P d，8”。第 11 组包含 “A g, 9”。组 12 包含 “C d, 10”。这十个有子外壳 4 d。组 13 包含 “I n，1”。组 14 包含 “S n, 2”。组 15 包含 “S b, 3”。第 16 组包含 “T e，4”。第 17 组包含 “我，5”。第 18 组包含 “X e，6”。这六个有子壳 5 p。时期 6，组 1 包含 “C s，1”。组 2 包含 “B a, 2”。这两个有子壳 6 s。组 3 包含 “L a, 1”，还有一个额外的星号。第 4 组包含 “H f, 2”。第 5 组包含 “T a，3”。第 6 组包含 “W, 4”。第 7 组包含 “R e，5”。第 8 组包含 “O s，6”。第 9 组包含 “我，7”。第 10 组包含 “P t, 8”。第 11 组包含 “A u，9”。第 12 组包含 “H g，10”。这 10 个有子壳 5 d。组 13 包含 “T l，1”。组 14 包含 “P b，2”。组 15 包含 “B i, 3”。第 16 组包含 “P o, 4”。第 17 组包含 “A t, 5”。第 18 组包含 “R n, 6”。这六个有子壳 6 p。时期 7，组 1 包含 “F r，1”。组 2 包含 “R a, 2”。这两个有子壳 7 s。组 3 包含 “A c, 1”，还有一个额外的双星号。第 4 组包含 “R f, 2”。第 5 组包含 “D b, 3”。第 6 组包含 “S g, 4”。第 7 组包含 “B h，5”。第 8 组包含 “H s，6”。第 9 组包含 “M t，7”。第 10 组包含 “D s，8”。第 11 组包含 “R g，9”。组 12 包含 “C n, 10”。这 10 个有子壳 6 d。组 13 包含 “U u t，1”。第 14 组包含 “F l，2”。第 15 组包含 “U u p，3”。第 16 组包含 “L v，4”。第 17 组不见了。第 18 组包含 “U u o，6”。这五个有子外壳 7 p。箭头将句点 6 和 7、组 3 与另外一个分为两行、每行有 14 列的部分连接起来。这些列没有编号。第一行用星号标记，其中的所有元素都有子壳 4 f。该行中的方框按顺序包含：C e、1、P r、2、N d、3、P m、5、E u、6、G d、7、T b、8、D y、9、H o、10、E r、11、T m、12、Y b、13，L u，14。第二行用双星号标记，其中的所有元素都有子壳 5 f。该行中的方框按顺序包含：T h 1、P a、2、U、3、N p、4、P u、5、A m、6、C m、7、B k、8、C f、9、E s、10、F m、11、M d、12、N o、13、L r，14。 — 图\(\PageIndex{1}\)：元素周期表，显示贝壳和子壳的结构。

第二行对应于 2 s 和 2 p 子壳。对于锂 (Li)（左上角），1 s 外壳充满自旋和向下旋转的电子 (↑↓)，2 s 外壳充满自旋或向下旋电子 (↑ 或 ↓)。因此，它的电子配置为\(1s^22s^1\)或 [He] 2 s，其中 [He] 表示氦核。像氢一样，最外层壳中的唯一电子很容易与其他原子共享。对于 beryllium (Be)，2 s 外壳充满了向上自旋和向下旋转的电子 (↑↓)，并具有电子配置 [He]\(2s^2\)。

接下来，我们看一下桌子的右边。对于硼 (B)，1 s 和 2 s 壳被填充，2 p (\(l = 1\)) 壳包含向上旋转或向下旋转的电子 (↑或↓)。从碳（C）到霓虹灯（N），我们填充 2 p 外壳。 2 p 壳中的最大电子数为\(4l + 2 = 4(2) + 2 = 6\)。对于霓虹灯 (Ne)，1 s 外壳充满了向上自旋和向下旋转的电子 (↑↓)，2 p 外壳充满了六个电子 (↑↓ ↑↑↑ ↓)。这 “填充” 了 1 s、2 s 和 2 p 的子壳，所以像氦气一样，霓虹原子往往不会与其他原子共享电子。

电子填充过程在第三行重复。但是，从第四行开始，模式被打破了。电子填充顺序的实际顺序由下式给出

1 s、2 s、2 p、3 s、3 p、4 s、3 d、4 p、5 s、4 d、5 p、6 s、4 f、5 d、6 p，7 s，...

请注意，3 d、4 d、4 f 和 5 d 子壳（粗体）是按顺序填充的；这是由于原子中电子之间的相互作用，到目前为止我们一直忽略了这一点。 过渡金属是前两列和最后六列间隙中的元素，其中包含填充 d (\(l = 1\)) 子壳的电子。不出所料，这些原子是按柱状排\(4l + 2 = 4(2) + 2 = 10\)列的。元素周期表的结构可以通过总能量 (n)、轨道角动量 (l) 和自旋 (s) 的量化来理解。前两列对应于 s (\(l = 0\)) 子壳，接下来的六列对应于 p (\(l = 1\)) 子壳，这些列之间的间隙对应于 d (\(l = 2\)) 子壳。

元素周期表还提供了有关分子键的信息。要了解这一点，请考虑最左列中的原子（所谓的碱金属，包括：锂、钠和钾）。这些原子在 2 s 子壳中含有单个电子，很容易捐赠给其他原子。相比之下，右二列中的原子（卤素：例如Cl、F和Br）在共享电子方面相对小气。这些原子宁愿接受电子，因为它们比填充的外壳（“高贵”）还差一个电子。

因此，如果将钠原子放置在靠近氯原子的地方，则钠原子会自由捐赠其 2 秒的电子，而 Cl 原子急切地接受它。在此过程中，钠原子（最初是中性电荷）变成带正电荷，Cl（最初是中性电荷）变成带负电荷。带电原子被称为离子。在这种情况下，离子是\(Na^+\)和\(Cl^-\)，上标表示离子的电荷。这些原子之间的电（库仑）吸引形成了 NaCl（盐）分子。两个离子之间的化学键称为离子键。化学键的种类很多。例如，在氧分子中，\(O_2\)电子在原子之间平均共享。氧原子的键合就是共价键的一个例子。