8.6: 原子光谱和 X 射线
- Page ID
- 202218
在本节结束时,您将能够:
- 用原子能水平和能量差异描述辐射的吸收和发射
- 使用量子数估计多电子原子中原子转变产生的光子的能量、频率和波长
- 解释原子荧光和 X 射线背景下的辐射概念
原子光谱研究提供了我们关于原子的大部分知识。 在现代科学中,原子光谱用于识别一系列物体中的原子种类,从遥远的星系到犯罪现场的血液样本。
原子光谱学的理论基础是电子在原子能级之间的过渡。 例如,如果氢原子中的电子从向\(n = 2\)壳过渡,则该原子会发射波长为一定波长的光子\(n = 3\)
\[\lambda = \frac{c}{f} = \frac{h \cdot c}{h \cdot f} = \frac{hc}{E_3 - E_2}, \nonumber \]
光子带走的能量在哪里\(\Delta E = E_3 - E_2\),\(hc = 1240 \, eV \cdot nm\). 这种辐射通过光谱仪后,它在屏幕上显示为一条清晰的光谱线。 该过程的玻尔模型如图所示\(\PageIndex{1}\)。 如果电子后来用能量吸收光子\(\Delta E\),电子就会返回\(n = 3\)外壳(我们之前研究过玻尔模型)。
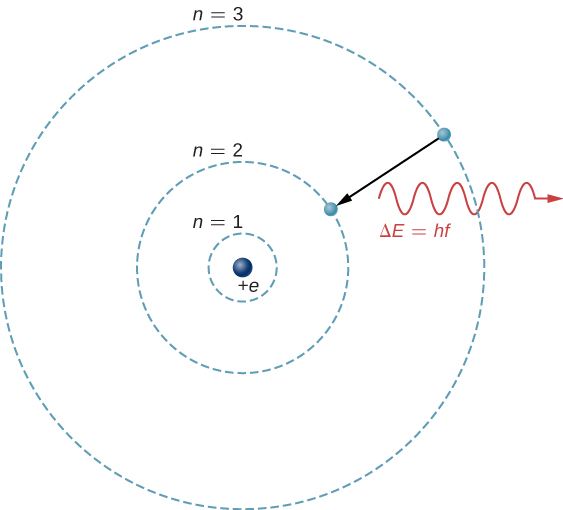
要了解多电子原子中的原子转变,必须考虑许多效应,包括电子之间的库仑排斥和内部磁相互作用(自旋轨道和自旋耦合)。 幸运的是,这些系统的许多特性可以通过忽略电子之间的相互作用并用其自己的单粒子波函数来表示每个电子来理解\(ψ_{nlm}\)。
原子过渡必须遵守选择规则。 这些规则来自量子力学和对称性原理。 选择规则将过渡分为允许或禁止。 (确实会出现禁止的过渡,但典型的禁止过渡的概率很小。) 对于类氢原子,涉及电磁相互作用(光子的发射和吸收)的原子转变遵循以下选择规则:
\[\Delta l = \pm 1, \label{select1} \]
其中\(l\)与轨道角动量的大小有关,
\[L = \sqrt{l(l + 1)}\hbar. \nonumber \]
对于多电子原子,类似的规则也适用。 为了说明这条规则,请考虑观察到的氢(H)、钠(Na)和汞(Hg)中的原子转变(图\(\PageIndex{2}\))。 此图中的水平线对应于原子能等级,此选择规则允许的过渡由在这些等级之间绘制的线条显示。 这些状态的能量大约为几电子伏特,过渡中发射的光子在可见范围内。 从技术上讲,原子过渡可能违反选择规则,但这种过渡并不常见。
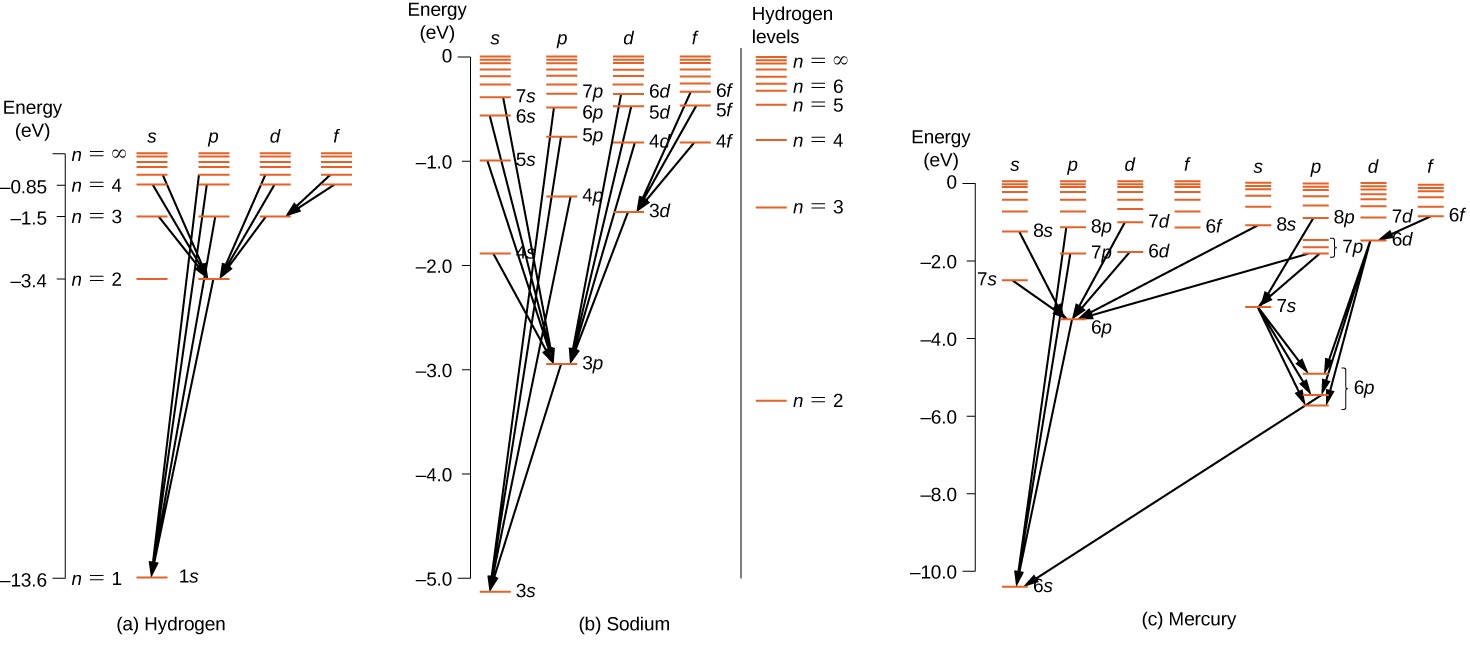
氢原子的能级图最简单。 如果我们忽略电子自旋,则所有具有相同值为 n 的状态的总能量相同。 但是,自旋轨道耦合将\(n = 2\)状态分为两个能量略有不同的角动量态(s 和 p)。 (这些关卡不会垂直移动,因为能量分解太小,无法显示在此图中。) 同样,自旋轨道耦合将\(n = 3\)状态分为三个角动量态(s、p 和 d)。
氢气的能级图与钠类似,因为两个原子的外壳中都有一个电子。 钠的价电子在被内壳电子屏蔽的原子核的电场中移动,因此它不会经历简单的 1/ r 库仑势,其总能量同时取决于 n 和 l。 有趣的是,水星有两个单独的能级图;这些图对应于其6 秒(价)电子的两个净自旋态。
用光谱仪分析钠的光谱。 观察到两条间隔紧密的线,波长分别为589.00 nm和589.59 nm。
- 如果 doublet 对应于从某种激发态向下过渡到 3 s 态的激发(价)电子,那么最初的电子角动量是多少?
- 这两个激发态之间的能量差是多少?
策略
钠和氢属于元素周期表的同一列或化学组,因此钠是 “氢样的”。 钠中最外层的电子在 3 s (\(l=0\)) 子壳中,可以被激发到更高的能量水平。 至于氢气,随后向较低能量水平的过渡必须遵守选择规则(方程\ ref {select1}):
\[\Delta l = \pm 1 \nonumber \]
我们必须首先确定满足选择规则的初始态的量子数。 然后,我们可以使用这个数字来确定初始状态的轨道角动量的大小。
解决方案
- 允许的过渡必须遵守选择规则。 如果初始态的量子数为\(l = 0\),则禁止过渡,因为\(\Delta l = 0\)。 如果初始态的量子数是,\(l = 2,3,4,...\)则禁止过渡,因为\(\Delta l > 1\)。 因此,初始状态的量子必须为\(l=1\)。 初始状态的轨道角动量为\[L = \sqrt{l(l + 1)}\hbar = 1.41 \hbar. \nonumber \]
- 由于两个过渡的最终状态相同(3 秒),因此光子的能量差等于两个激发态的能量差。 用这个方程\[\Delta e = hf = h\left(\frac{c}{\lambda}\right), \nonumber \]我们有\[\begin{align*} E &= hc\left(\frac{1}{\lambda_1} - \frac{1}{\lambda_2}\right) \\[4pt] &=(4.14 \times 10^{-15} eVs)(3.00 \times 10^8 m/s) \times \left(\frac{1}{589.00 \times 10^{-9} m} - \frac{1}{589.59 \times 10^{-9} m}\right) \\[4pt] &= 2.11 \times 10^{-3} eV. \end{align*} \nonumber \]
意义
为了理解测量这种能量差的难度,我们将这种差异与过渡期间发射的两个光子的平均能量进行了比较。 给定平均波长为 589.30 nm,光子的平均能量为
\[E = \frac{hc}{\lambda} = \frac{(4.14 \times 10^{-15} eVs) (3.00 \times 10^8 m/s)}{589.30 \times 10^{-9} m} = 2.11 \, eV. \nonumber \]
能量差约\(\Delta E\)为该平均能量的0.1%(千分之一)。 但是,灵敏的光谱仪可以测量差异。
原子荧光
当原子中的电子被高能紫外线(UV)光子的吸收激发到比基态高出几步时,就会产生荧光。 一旦激发,电子就会以两种方式 “去激发”。 电子可以回落到基态,发射与激发它的能量相同的光子,或者它可以在一系列较小的步骤中掉落,发射几个低能光子。 其中一些光子可能在可见范围内。 衣服中的荧光染料可以通过将紫外线辐射转化为可见光,使颜色在阳光下看起来更亮。 荧光灯在将电能转化为可见光方面比白炽灯更有效(效率约为白炽灯的四倍)。 \(\PageIndex{3}\)该图显示了被紫外线灯照亮的蝎子。 皮肤表面附近的蛋白质会发出典型的蓝光。

X 射线
对原子能转变的研究使我们能够理解 X 射线和 X 射线技术。 像所有电磁辐射一样,X 射线是由光子组成的。 当原子最外壳中的电子掉落到内壳时,就会产生 X 射线光子。 (氢原子不发射 X 射线,因为电子能级间隔太近,无法发射高频辐射。) 这种过渡通常是禁止的,因为较低的状态已经被填满。 但是,如果内壳有空位(缺少内部电子,可能是因为被高速电子击倒),则来自其中一个外壳的电子可能会掉落能量以填补空缺。 这种过渡的能量间隙相对较大,因此辐射的X射线光子的波长相对较短。
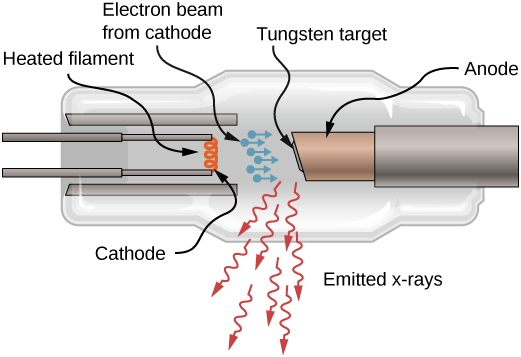
也可以通过用高能电子轰击金属目标来产生 X 射线,如图所示\(\PageIndex{4}\)。 在图中,电子从灯丝中煮沸,然后通过电场加速成钨靶材。 根据经典的电磁学理论,任何加速的带电粒子都会发出辐射。 因此,当电子撞击钨靶并突然减速时,电子会发出制动辐射(通常使用德语中的术语:Bremsstrahlung)。 制动辐射是指任何被介质减速的带电粒子产生的辐射。 在这种情况下,制动辐射包含连续的频率范围,因为电子将以略有不同的方式与目标原子碰撞。
制动辐射并不是这种相互作用中产生的唯一辐射类型。 在某些情况下,电子会与目标原子的另一个内壳电子碰撞,然后将电子从原子台球风格中击出。 当较高外壳中的电子掉入状态(能量水平下降)并发射 X 射线光子时,空状态就会被填充。
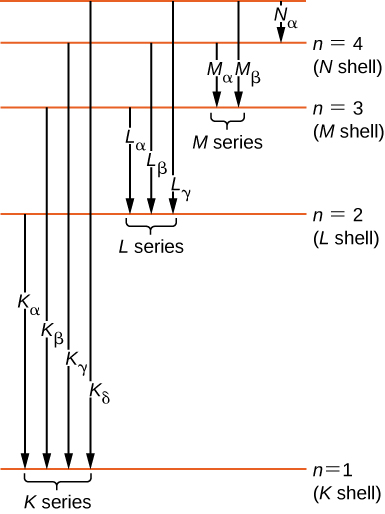
从历史上看,X 射线光谱线是用字母(K、L、M、N...)标记的。 这些字母对应于原子壳 (\(n = 1,2,3,4,...\))。 从任何更高的外壳过渡到 K (\(n = 1\)) 壳所产生的 X 射线被标记为 K X 射线。 从 L (\(n = 2\)) 壳过渡过程中产生的 X 射线称为\(K_{\alpha}\) X 射线;从 M (\(n = 3\)) 壳过渡过程中产生的 X 射线称为\(K_{\beta}\) X 射线;从 N (\(n = 4\)) 壳过渡时产生的 X 射线被称为 X 射线\(K_{\gamma}\)X 射线;依此类推。 从较高炮弹到 L 和 M 壳的过渡标记类似。 这些转变由图中的能量等级图表示\(\PageIndex{5}\)。
图中给出了用电子束撞击金属所产生的 X 射线波长的分布\(\PageIndex{6}\)。 目标金属中的 X 射线过渡以峰值的形式出现在制动辐射曲线的顶部。 与 X 射线分布中的峰值相对应的光子频率称为特征频率,因为它们可用于识别目标金属。 尖锐的截止波长(略低于\(K_{\gamma}\)峰值)对应于将所有能量丢失给单个光子的电子。 节能禁止波长较短的辐射。
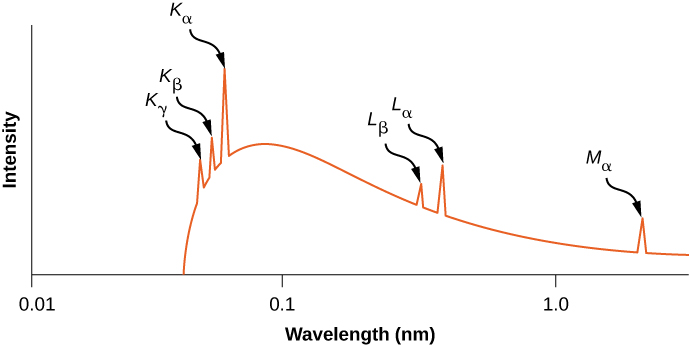
估计铝的\(K_{\alpha}\) X 射线的特征能量和频率 (\(Z = 13\))。
策略
\(K_{\alpha}\)X 射线是由 L (\(n=2\)) 壳中的电子过渡到 K (\(n = 1\)) 壳产生的。 L 壳中的电子 “看见” 有效电荷\(Z = 13 - 1 = 12\),因为 K 壳中的一个电子可以屏蔽核电荷。 (回想一下,两个电子不在 K 壳中,因为另一个电子态空置。) 发射光子的频率可以根据 L 和 K 壳之间的能量差来估算。
解决方案
氢原子中 L 壳和 K 壳之间的能量差为 10.2 eV。 假设 L 壳或更高能量炮弹中的其他电子无法屏蔽核电荷,则原子中 L 和 K 壳之间的能量差约\(Z = 13\)为
\[\begin{align*} E_{L \rightarrow K} &\approx (Z - 1)^2 (10.2 \, eV) \\[4pt] &\approx (13 - 1)^2(10.2 \, eV) \\[4pt] &\approx 1.47 \times 10^3 eV. \end{align*} \nonumber \]
根据这种关系\(f = (\Delta E_{L \rightarrow K})/h\),X射线的频率是
\[f = \frac{1.47 \times 10^3 eV}{4.14 \times 10^{-15} eV \cdot s} = 3.55 \times 10^{17} Hz. \nonumber \]
意义
典型的 X 射线波长为 0.1—10 nm。 在这种情况下,波长为:
\[\lambda = \frac{c}{f} = \frac{3.0 \times 10^8 m/s}{3.55 \times 10^{17} Hz} = 8.5 \times 10^{-10} = 0.85 \, nm. \nonumber \]
因此,铝中的过渡 L → K 会产生 X 射线辐射。
X 射线生产为量子力学提供了重要的考验。 根据玻尔模型,\(K_{\alpha}\)X 射线的能量取决于核电荷或原子序数 Z。 如果 Z 很大,则原子中的库仑力很大,能量差 (\(\Delta E\)) 很大,因此,辐射光子的能量很大。 举例来说,以多电子原子中的单个电子为例。 忽略电子之间的相互作用,允许的能量水平是
\[E_n = -\frac{Z^2(13.6 \, eV)}{n^2}, \nonumber \]
其中 n = 1、2、... 而 Z 是原子核的原子序数。 但是,L (\(n = 2\)) 壳中的电子 “看见” 了电荷\(Z - 1\),因为 K 壳中的一个电子可以屏蔽核电荷。 (回想一下,K 壳中只有一个电子,因为另一个电子被 “击倒” 了。) 因此,L 和 K 壳中电子的近似能量为
\[E_L \approx - \frac{(Z - 1)^2(13.6 \, eV)}{2^2} \nonumber \]
\[E_K \approx - \frac{(Z - 1)^2(13.6 \, eV)}{1^2}. \nonumber \]
因此,在从 L 壳过渡到 K 壳的过程中,光子带走的能量是
\[ \begin{align*} \Delta E_{L \rightarrow K} &= (Z - 1)^2 (13.6 \, eV)\left(\frac{1}{1^2} - \frac{1}{2^2} \right) \\[4pt] &= (Z - 1)^2 (10.2 \, eV), \end{align*} \nonumber \]
其中 Z 是原子数。 一般来说,从外壳过渡到 K 壳的 X 射线光子能量为
\[E_{L\rightarrow K} = hf = constant \times (Z - 1)^2, \nonumber \]
要么
\[(Z - 1) = constant \sqrt{f}, \nonumber \]
其中\(f\)是\(K_{\alpha}\) X 射线的频率。 这个方程是莫斯利定律。 对于较大的值\(Z\),我们大约有
\[Z \approx constant \sqrt{f}. \nonumber \]
可以通过测量\(f\)各种金属目标来检查这种预测。 如果 Z 与\(\sqrt{f}\)数据的对比图(称为 Moseley 图)为线性图,则支持此模型。 图中显示了 K 和 L 系列的模型预测和实验结果的比较\(\PageIndex{7}\)。 这些数据支持这样的模型,即当外壳电子下降能量以填补内壳的空位时,就会产生 X 射线。
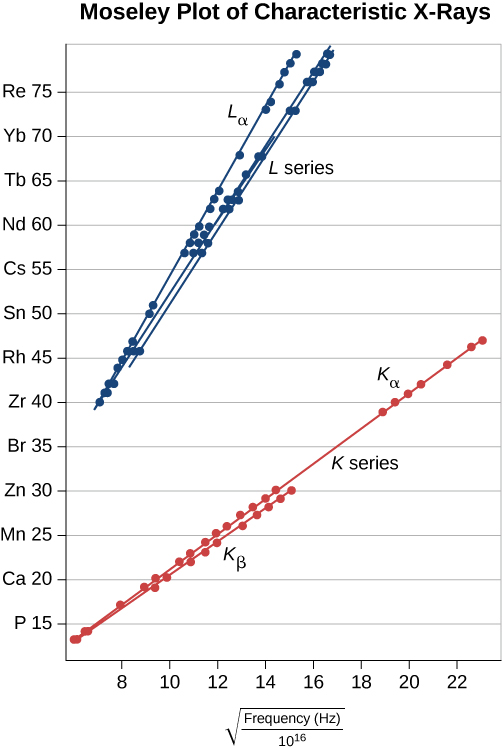
X 射线是通过用高能电子轰击金属目标而产生的。 如果目标被另一个原子序数两倍的目标所取代,那么 X 射线的频率会怎样?
- 回答
-
频率四倍
计算\(K_{\alpha}\) X 射线管中钨阳极产生的 X 射线的大致能量。
策略
两个电子占据一个填充的 K 壳。 该壳中的空位会留下一个电子,因此 L 壳中电子的有效电荷将为 Z − 1 而不是 Z。 对于钨,Z=74,因此有效电荷为 73。 这个数字可以用来计算 L 和 K 壳之间的能级差,从而计算光子在过渡 L→K 中带走的能量。
解决方案
有效 Z 为 73,因此\(K_{\alpha}\) X 射线能量由下式给出
\[E_{K_{\alpha}} = \Delta E = E_i - E_f = E_2 - E_1, \nonumber \]
哪里
\[E_1 = - \frac{Z^2}{1^2}E_0 = - \frac{73^2}{1}(13.6 \, eV) = - 72.5 \, keV \nonumber \]
和
\[E_2 = - \frac{Z^2}{2^2}E_0 = - \frac{73^2}{4}(13.6 \, eV) = -18.1 \, keV. \nonumber \]
因此,
\[E_{K_{\alpha}} = - 18.1 \, keV - (- 72.5 \, keV) = 54.4 \, keV. \nonumber \]
意义
这种大的光子能量是 X 射线的典型特征。 较重元素的X射线能量会逐渐变大,因为它们的能量大约增加为\(Z^2\) 要从钨原子 “击倒” 内部电子,需要超过50,000伏特的加速电压。
X 射线技术
X 射线有许多应用,例如医疗诊断(图\(\PageIndex{8}\))、机场行李检查(图\(\PageIndex{9}\)),甚至检测飞机关键部件的裂缝。 最常见的 X 射线图像是由阴影引起的。 由于 X 射线光子具有高能量,因此它们会穿透对可见光不透明的材料。 X射线光子拥有的能量越多,它穿透的材料就越多。 穿透深度与材料的密度以及光子的能量有关。 材质越密集,穿过的 X 射线光子越少,阴影越暗。 X 射线可有效识别骨折和肿瘤;但是,过度暴露于 X 射线会损害生物体中的细胞。
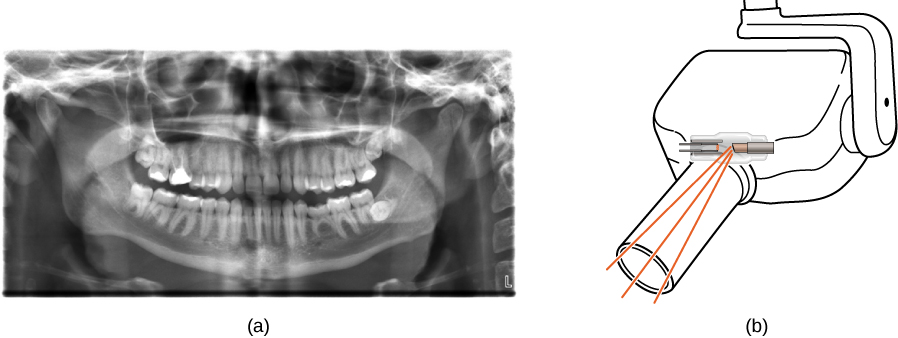

标准 X 射线图像提供物体的二维视图。 但是,在医疗应用中,这种观点通常无法提供足够的信息来得出确切的结论。 例如,在人体的二维 X 射线图像中,骨骼可以很容易地隐藏软组织或器官。 CAT(计算机轴向断层扫描)扫描仪通过在全身 “切片” 中收集大量 X 射线图像来解决这个问题。 对不同方向上X射线的相对吸收进行复杂的计算机图像处理,可以生成非常详细的人体三维X射线图像。
X 射线也可用于探测原子和分子的结构。 以射入结晶固体表面的 X 射线为例。 一些 X 射线光子在表面反射,而另一些则从表面下方的原子 “平面” 反射。 对于不同的入射角度,这些光子之间的干扰会在屏幕上产生漂亮的图像(图\(\PageIndex{10}\))。 X 射线与固体的相互作用称为 X 射线衍射。 使用X射线衍射最著名的例子是发现了DNA的双螺旋结构。



