8.4: 电子自旋

Last updated
Save as PDF

Page ID: 202236

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

用五个量子数表示氢原子中电子的状态
使用量子数计算电子自旋和磁矩的大小和方向
用氢原子内部的磁相互作用来解释氢光谱的精细和超精细结构

在本节中，我们将考虑电子自旋的影响。 Spin 在我们的氢原子模型中引入了另外两个量子数。两者都是通过观察原子光谱的精细结构发现的。自旋是所有粒子的基本特征，而不仅仅是电子，它类似于延伸物体围绕自身轴线的固有自旋，例如地球的每日自转。

自旋的量化方式与轨道角动量相同。已经发现，电子固有自旋角动量\(S\)的大小由下式给出

\[S = \sqrt{s(s + 1)}\hbar, \nonumber \]

其中\(s\)，定义为自旋量子数。这与量化类似\(L\)，唯一的不同是电子唯一允许\(s\)的值是\(s = 1/2\)。据说电子是 “半自旋粒子”。自旋投影量子数与自旋\(m_s\)的 z 分量有关，表示为

\[S_z = m_s\hbar. \label{eq2} \]

通常，允许的量子数是

\[m_s = -s, -s + 1, . . ., 0, . . ., +s - 1, s. \nonumber \]

对于电子 (\(s = 1/2\)) 的特殊情况，

\[m_s = -\frac{1}{2} \text{ or } \frac{1}{2}. \nonumber \]

固有自旋的方向是量化的，就像轨道角动量一样。该\(m_s = -1/2\)状态被称为 “spid-down” 状态，具有自旋的 z 分量\(s_z = -1/2\)，该\(m_s = +1/2\)状态被称为 “spin-up” 状态，具有自旋的 z 分量\(s_z = +1/2\)。这些状态如图所示\(\PageIndex{1}\)。

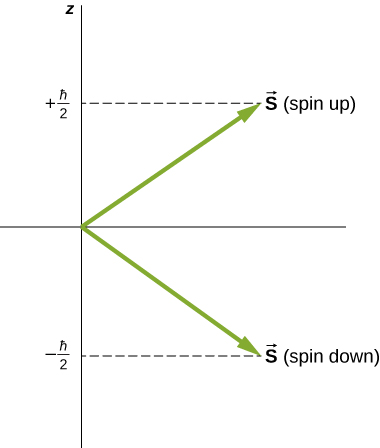
电子的两种可能的自旋态被描述为长度相等的向量，一个指向上和向右，代表向量 S 向上旋转，另一个指向下和向右，代表自旋向下。这两个向量与水平方向的角度相同。 Spin up 的 z 分量为加 h bar 大于 2，而向下旋转的 z 分量为负 h bar 大于 2。 — 图\(\PageIndex{1}\)：电子自旋的两种可能状态。

电子的固有磁偶极矩\(\mu_e\)也可以用自旋量子数来表示。与轨道角动量类比，电子磁矩的大小为

\[\mu_s = \left(\frac{e}{2m_e}\right)S. \nonumber \]

根据狭义相对论，该值低2倍。因此，在矢量形式中，自旋磁矩为

\[\vec{\mu} = \left(\frac{e}{m_e}\right)\vec{S}. \nonumber \]

磁矩的 z 分量为（来自方程\ ref {eq2}）

\[\begin{align} \mu_z &= - \left(\frac{e}{m_e}\right) S_z \\[5pt] &= - \left(\frac{e}{m_e}\right) m_s \hbar. \end{align} \nonumber \]

自旋投影量子数只有两个值 (\(m_s = \pm1/2\))，因此磁矩的 z 分量也只有两个值：

\[\mu_z = \pm \left(\frac{e}{2m_e}\right) = \pm \mu_B\hbar, \nonumber \]

玻\(\mu_B\)尔磁铁在哪里。电子是磁性的，所以我们期望电子与其他磁场相互作用。我们考虑两个特殊情况：自由电子与外部（不均匀）磁场的相互作用，以及氢原子中的电子与电子轨道角动量产生的磁场的相互作用。

外场中的电子

Stern-Gerlach 实验提供了实验证据，证明电子具有自旋角动量。该实验使银 (Ag) 原子流穿过外部不均匀的磁场。银原子的轨道角动量为零，外壳中包含一个未成对的电子。因此，银原子的总角动量完全归因于外部电子的自旋 (\(s = 1/2\))。由于电子自旋，银原子在穿过磁场时充当微小的磁铁。这些 “磁铁” 有两个可能的方向，分别对应于电子的自旋向上和向下旋状态。磁场将自旋向上的原子转移到一个方向，将向下旋转的原子转移到另一个方向。这会在屏幕上产生两个不同的波段（图\(\PageIndex{2}\)）。

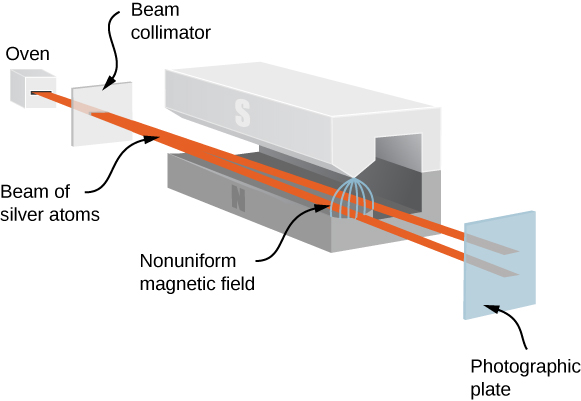
该图显示了 Stern Gerlach 实验的插图。一束银原子离开烤箱，在穿过狭缝时被准直。准直光束进入磁体。当光束在磁体的两极之间穿过时，不均匀的磁场会导致光束一分为二。一部分朝北极方向移动，另一部分朝南极方向移动。两根光束离开磁铁，在两个不同的地方撞击照相板。 — 图\(\PageIndex{2}\)：在 Stern-Gerlach 实验中，外部不均匀的磁场将电子束转移到两个不同的方向。该结果归因于自旋角动量的量化。

根据经典的预测，银原子的角动量（以及磁矩）可以指向任何方向，因此人们预计屏幕上会有持续的污迹。由此产生的两个Stern-Gerlach实验波段为量子力学的思想提供了惊人的支持。

访问 Phet Explorations：Stern-Gerlach 实验，了解有关 Stern-Gerlach 实验的更多信息。

示例\(\PageIndex{1}\): Electron Spin and Radiation in An external Magnetic field

处于基态的氢原子被置于外部均匀磁场中 (\(B = 1.5 \, T\))。确定电子在自旋向上和向下旋转状态之间的过渡中产生的辐射频率。

策略

自旋投影量子数是\(m_s = \pm 1/2\)，所以磁矩的 z 分量是

\[\mu_z = \pm \left(\frac{e}{2m_e} \right) = \pm \mu_B \hbar. \nonumber \]

与电子磁矩和外部磁场之间的相互作用相关的势能是

\[\begin{align*} U &= - \mu_z B \\[5pt] &= \mp \mu_BB. \end{align*} \nonumber \]

发出的光的频率与这两种状态之间的能量 (\(\Delta E\)) 差成正比。

解决方案

这些状态之间的能量差为\(\Delta E = 2\mu_BB\)，因此产生的辐射频率为

\[\begin{align*} f = \dfrac{\Delta E}{h} &= \frac{2\mu_BB}{h} \\[5pt] &= \frac{2\left(5.79 \times \frac{10^{-5} eV}{T}\right)(1.5 \, T)}{4.136 \times 10^{-15} eV \cdot s} \\[5pt] &= 4.2 \times 10^{10} \, \frac{cycles}{s}. \end{align*} \nonumber \]

意义

电子磁矩与外部磁场耦合。无论电子与质子是否对齐，该系统的能量都不同。这些状态之间过渡产生的辐射频率与能量差成正比。如果我们将磁场的强度提高一倍，使所有其他因素保持不变，辐射的频率就会加倍，其波长会被切成两半。

练习\(\PageIndex{1}\)

如果 Stern-Gerlach 实验产生了四个不同的波段而不是两个波段，那么关于带电粒子的自旋量子数可以得出什么结论？

回答: \(s = 3/2 <\)

自旋轨道耦合（精细结构）

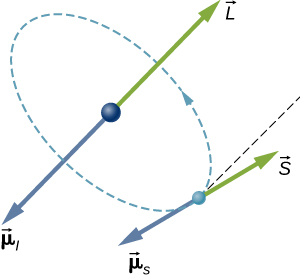
在氢原子中，电子磁矩可以与电子的轨道角动量产生的磁场相互作用，这种现象称为自旋轨道耦合。轨道角动量 (\(\vec{L}\))、轨道磁矩 (\(\vec{\mu}\))、自旋角动量 (\(\vec{S}\)) 和自旋磁矩 (\(\vec{\mu}_s\)) 向量一起显示在图中\(\PageIndex{3}\)。

正如氢原子的能级可以被外部磁场分裂一样，氢原子的能量水平也可以被原子的内部磁场分开。如果电子的磁矩和电子的轨道磁矩是反平行的，则磁相互作用产生的势能相对较高，但是当这些矩平行时，势能相对较小。从这两种状态过渡到较低的能量水平会导致发射频率略有不同的光子。也就是说，自旋轨道耦合 “分裂” 了来自无自旋电子的预期光谱线。氢光谱的精细结构由自旋轨道耦合来解释。

原子中电子的轨道被描述为围绕圆心较大球体的圆形轨道上的一个小球体。行进方向是右手的（如果向下看，则是逆时针方向。）在原子核处，向量 L 指向上方（同样，从上方看），向量 mu sub l 指向下方。在电子处，矢量 S 相对于 L 的方向指向一个未指定的角度，而向量 mu sub s 指向与 S 相反的方向。 — 图\(\PageIndex{3}\)：自旋轨道耦合是电子的自旋磁矩\(\vec{mu}_s\)与其轨道磁矩的相互作用\(\vec{\mu}_l\)。

电子自旋-核自旋耦合（超精细结构）

就像电子一样，质子自旋1/2，具有磁矩。（根据核理论，这一刻是由于质子内夸克的轨道运动造成的。）氢光谱的超精细结构可以通过质子的磁矩和电子的磁矩之间的相互作用来解释，这种相互作用被称为自旋自旋耦合。电子质子系统的能量因力矩是否对齐而有所不同。这些状态之间的过渡（自旋翻转变）会导致发射波长为\(\lambda = 21\) cm（在无线电范围内）的光子。原子光谱学中的21厘米线是氢气的 “指纹”。天文学家利用这条光谱线绘制星系的螺旋臂图，这些星系主要由氢气组成（图\(\PageIndex{4}\)）。

风车星系的三张望远镜图像。在图 a 中，图像是可见光。银河系以恒星的集合形式出现，中心非常密集，手臂呈螺旋状。图 b 是 21 厘米的辐射图像。在这张照片中，螺旋性质更为明显，中央凸起不存在。图 c 叠加了可见图像和 21 c m 图像。 — 图\(\PageIndex{4}\)：氢原子中电子和质子之间的磁相互作用用于绘制风车星系（NGC 5457）的螺旋臂。 (a) 在可见光下看到的星系；(b) 在 21 厘米氢辐射下看到的星系；(c) (a) 和 (b) 的合成图像。注意氢气发射是如何穿透银河系中的尘埃以非常清楚地显示螺旋臂的，而银河核在可见光下表现得更好（来源 a：欧空局和美国宇航局对作品的修改；来源 b：Fabian Walter 对作品的修改）。

氢原子中电子状态的完整规格需要五个量子数：n、l、m、s 和\(m_s\)。表中总结了这些量子数的名称、符号和允许值\(\PageIndex{4}\)。

表\(\PageIndex{4}\)：氢原子中电子的量子数摘要
姓名	符号	允许的值
主量子数	n	1、2、3、...
角动量	l	0、1、2、... n — 1
角动量投影	m	\(0, \pm 1, \pm 2, . . . \pm l\)
旋转	s	1/2（电子）
旋转投影	\(m_s\)	\(- 1/2, \, +1/2\)

请注意，本节（\(s\)和\(m_s\)）中介绍的固有量子数对许多粒子有效，而不仅仅是电子。例如，原子核内的夸克也是自旋半粒子。正如我们稍后将看到的那样，量子数有助于对亚原子粒子进行分类，并进入试图解释宇宙如何运作的科学模型。