8.3: 电子的轨道磁偶极矩
- Page ID
- 202203
在本节结束时,您将能够:
- 解释为什么氢原子具有磁特性
- 解释为什么与轨道角动量相关的氢原子的能量水平会被外部磁场分开
- 使用量子数计算氢原子的轨道磁偶极矩的大小和方向
在玻尔的氢原子模型中,电子在围绕质子的圆形轨道上移动。 电子在一定时间内经过回路上的特定点,因此我们可以计算出电流\(I = Q/t\)。 因此,在氢原子中绕质子运行的电子类似于流经圆线的电流(图\(\PageIndex{1}\))。 在磁学研究中,我们发现载流线会产生磁场。 因此,可以合理地得出结论,氢原子会产生磁场并与其他磁场相互作用。
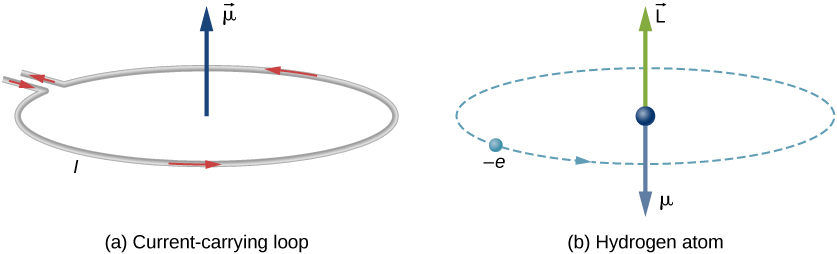
轨道磁偶极矩是衡量电子轨道角动量产生的磁场强度的指标。 从电流回路上的力和扭矩来看,电流回路的轨道磁偶极矩的大小为
\[\mu = IA, \nonumber \]
哪里\(I\)是电流,\(A\)是回路的面积。 (为简洁起见,我们将其称为磁矩。) 与围绕氢原子中质子的轨道上的电子\(I\)相关的电流是
\[I = \dfrac{e}{T}, \label{eq1} \]
其中 e 是电子电荷的大小,\(T\)是其轨道周期。 如果我们假设电子在完美的圆形轨道上移动,则轨道周期为
\[T = \dfrac{2\pi r}{v}, \nonumber \]
其中 r 是轨道的半径,v 是电子在其轨道上的速度。 假设圆的面积为\(\pi r^2\),则绝对磁矩为
\[\mu = IA = \dfrac{e}{\left(\dfrac{2\pi r}{v}\right)}\pi r^2 = \dfrac{evr}{2}. \nonumber \]
用轨道角动量 (\(\vec{L} = \vec{r} \times \vec{p}\)) 来表示磁动量 μμ很有帮助。 因为电子围成一个圆圈,所以位置向量\(\vec{r}\)和动量向量\(\vec{p}\)形成直角。 因此,轨道角动量的大小为
\[L = |\vec{L}| = |\vec{r} \times \vec{p}| = rp \, \sin \, \theta = rmv. \label{eq2} \]
将这两个方程组合起来,我们有
\[\mu = \left(\dfrac{e}{2m_e}\right)L. \label{eq3} \]
以完整的矢量形式,此表达式写为
\[\vec{\mu} = - \left(\dfrac{e}{2m_e}\right)\vec{L}. \label{BIG} \]
出现负号是因为电子具有负电荷。 请注意,电子磁矩的方向与轨道角动量反平行,如图所示\(\PageIndex{1b}\)。 在原子的玻尔模型中,方程\ ref {BIG}\(\vec{L}\) 中\(\vec{\mu}\)和之间的关系与轨道半径无关。
磁矩\(μ\)也可以用轨道角量子数表示\(l\)。 结合方程\ ref {eq2} 和方程\ ref {eq1},磁矩的大小为
\[\mu = \left(\dfrac{e}{2m_e}\right)L = \left(\dfrac{e}{2m_e} \right) \sqrt{l(l + 1)}\hbar = \mu_B \sqrt{l(l + 1)}. \label{eq5} \]
磁矩的 z 分量为
\[ \begin{align} \mu_z &= -\left(\dfrac{e}{2m_e}\right) \, L_z \\[4pt] &= - \left(\dfrac{e}{2m_e}\right) \, m \hbar \\[4pt] &= - \mu_B m. \label{eq6} \end{align} \]
量\(\mu_B\)是磁性的基本单位,称为玻尔磁体,其值为\(9.3 \times 10^{-24} \, Joule/Tesla\) (J/T) 或\(5.8 \times 10^{-5} eV/T\)。 磁矩的量化是轨道角动量量化的结果。
正如我们将在下一节中看到的那样,氢原子的总磁偶极矩既是电子的轨道运动又是其固有自旋造成的。 现在,我们忽略了电子自旋的影响。
氢原子中处于 (a) s 态、(b) p 态和 (c) d 态的电子的轨道偶极子磁矩 μ的大小是多少? (假设电子的自旋为零。)
策略
电子的磁动量与其轨道角动量 L 有关。 对于氢原子,这个量与轨道角量子数 l 有关。 状态以光谱表示法给出,它将字母(s、p、d 等)与量子数联系起来。
解决方案
磁矩的大小在方程式\ ref {eq5} 中给出:
\[ \begin{align} \mu_z &= -\left(\dfrac{e}{2m_e}\right) \, L \nonumber \\[4pt] &= \left(\dfrac{e}{2m_e}\right) \, \sqrt{l(l + 1)} \hbar \nonumber \\[4pt] &= \mu_B\sqrt{l(l + 1)}. \end{align} \nonumber \]
- 对于 s 状态,\(l = 0\)所以我们有 an\(\mu = 0\) d\(\mu_z = 0\)。
- 对于 p 状态,我们有\(l = 0\) wher\[\mu = \mu_B\sqrt{1(1 + 1)} = \sqrt{2}\mu_B \nonumber \]\[\mu_z = -\mu_Bm \nonumber \] e s\(m = (-1, 0, 1)\) o\[\mu_z = \mu_B, \, 0, \, -\mu_B. \nonumber \]
- 对于 d 状态\(l = 2\),我们在\[\mu = \mu_B\sqrt{2(2 + 1)} = \sqrt{6}\mu_B \nonumber \]\[\mu_z = -\mu_Bm \nonumber \]哪里\(m = (-2, -1, 0, 1, 2)\)得到\[\mu_z = 2\mu_B, \, \mu_B \, 0, \, -\mu_B \, -2\mu_B. \nonumber \]
意义
在 s 状态下,没有轨道角动量,因此没有磁矩。 这并不意味着电子处于静止状态,只是说电子的整体运动不会产生磁场。 在 p 态下,电子有一个磁矩,该磁矩的 z 分量有三个可能的值;这意味着磁矩可以指向三个不同的极方向,每个方向都与轨道角动量向量反平行。 在 d 态下,电子有一个磁矩,该磁矩的 z 分量有五个可能的值。 在这种情况下,磁矩可以指向五个不同的极方向。
氢原子有磁场,因此我们预计氢原子会与外部磁场相互作用,例如两个条形磁体之间的推拉。 从电流回路上的力和扭矩来看,我们知道,当电流回路与外部磁场相互作用时\(\vec{B}\),它会经历由下式给出的扭矩
\[\vec{\tau} = I(\vec{A} \times \vec{B}) = \vec{\mu} \times \vec{B}, \nonumber \]
其中 I 是电流,\(\vec{A}\)是回路的面积,\(\vec{\mu}\)是磁矩,\(\vec{B}\)是外部磁场。 该扭矩用于旋转氢原子的磁矩矢量,使其与外部磁场对齐。 因为机械工作是由氢原子上的外部磁场完成的,所以我们可以谈谈原子中的能量转换。 与这种磁相互作用相关的氢原子的势能由方程\ ref {eq30} 给出:
\[U = -\vec{\mu} \cdot \vec{B}. \label{eq30} \]
如果磁矩与外部磁场反平行,则势能很大,但是如果磁矩与磁场平行,则势能很小。 因此,在氢原子上使原子的磁矩矢量朝外部磁场方向旋转的工作与势能的下降有关。 但是,系统的能量是保守的,因为势能的下降会产生辐射(光子的发射)。 这些能量转换是量化的,因为磁矩只能指向某些方向。
如果外部磁场指向正 z 方向,则与轨道磁偶极矩相关的势能为
\[U(\theta) = -\mu B \, cos \, \theta = - \mu_z B = - (-\mu_B m) = m\mu_BB, \nonumber \]
哪里\(\mu_B\)是玻尔磁子,m 是角动量投影量子数(或磁轨道量子数),其值为
\[m = -l, -l + 1, ..., 0, ..., l - 1, l. \nonumber \]
例如,在\(l = 1\)电子状态下,电子的总能量被分成三个不同的能量级,对应于\(U = -\mu_B B, 0, \mu_B B\)。
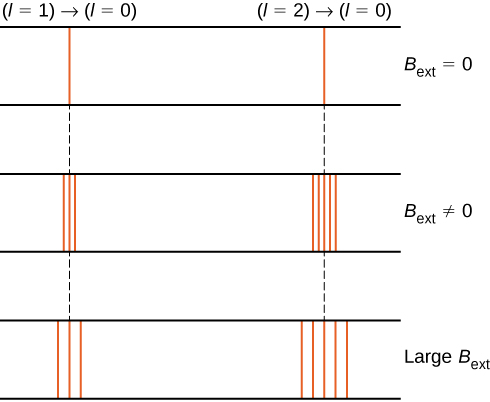
外部磁场对能级的分裂称为塞曼效应。 忽略电子自旋的影响,从\(l = 1\)状态过渡到常见的低能量状态会产生三条间隔紧密的光谱线(图\(\PageIndex{2}\),左栏)。 同样,从\(l = 2\)状态过渡会产生五条间隔紧密的光谱线(右列)。 这些线的分离与外部磁场的强度成正比。 这种效果有许多用途。 例如,太阳氢光谱中线的分裂用于确定太阳磁场的强度。 许多这样的磁场测量可用于绘制太阳表面磁活动的地图,称为磁图(图\(\PageIndex{3}\))。



