8.2: 氢原子
- Page ID
- 202268
在本节结束时,您将能够:
- 用波函数、概率密度、总能量和轨道角动量来描述氢原子
- 确定氢原子的每个量子数(n、l、m)的物理意义
- 区分原子的玻尔模型和薛定模型
- 使用量子数计算有关氢原子的重要信息
氢原子是自然界中最简单的原子,因此是研究原子和原子结构的良好起点。 氢原子由单个带负电荷的电子组成,它围绕带正电荷的质子移动(图\(\PageIndex{1}\))。 在玻尔的模型中,电子在完美的圆形轨道上被诱人的库仑力拉到质子周围。 质子的质量大约是电子的1800倍,因此质子在电子对质子的力作用下移动得很少。 (这类似于地球-太阳系统,在该系统中,太阳在地球施加的力作用下移动得很少。) 光子和物质波中使用牛顿定律解释了这种效应。
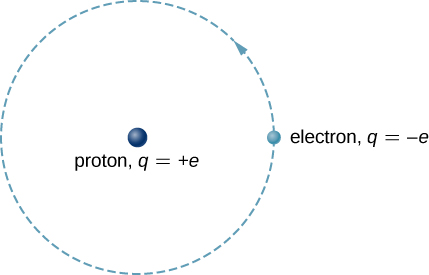
假设质子是固定的,我们专注于电子的运动。
在质子的电场中,电子的势能是
\[U(r) = -k\frac{e^2}{r}, \nonumber \]
其中\(k = 1/4\pi\epsilon_0\)\(r\) and 是电子和质子之间的距离。 正如我们之前看到的,物体上的力等于势能函数梯度(或斜率)的负值。 对于氢原子的特殊情况,电子和质子之间的力是一种有吸引力的库仑力。
请注意,势能函数\(U(r)\)不会随时间变化。 因此,薛定葛的氢原子方程简化为两个更简单的方程:一个仅依赖于空间(x,y,z),另一个仅取决于时间(t)。 (《量子力学》中讨论了将波函数分成与空间和时间相关的部分,以获得与时间无关的势能函数。) 我们对空间相关方程最感兴趣:
\[\frac{-\hbar}{2m_e}\left(\frac{\partial^2\psi}{\partial x^2} + \frac{\partial^2\psi}{\partial y^2} + \frac{\partial^2\psi}{\partial z^2}\right) - k\frac{e^2}{r}\psi = E\psi, \nonumber \]
其中\(\psi = psi (x,y,z)\)是电子的三维波函数,模因是电子的质量,\(E\)是电子的总能量。 回想一下\(\Psi (x,y,z,t)\),全波函数是空间相关波函数\(\psi = \psi(x,y,z)\)和随时间变化的波函数的乘积\(\varphi = \varphi(t)\)。
除了与时间无关外,还\(U(r)\)具有球形对称性。 这表明,如果我们用球坐标 (\(r, \theta, \phi\)) 而不是矩形坐标 () 来表达,我们可以更容易地求解薛定葛方程。\(x,y,z\) 球坐标系如图所示\(\PageIndex{2}\)。 在球坐标中,变量\(r\)\(\theta\)是径向坐标,是极角(相对于垂直 z 轴),\(\phi\)是方位角(相对于 x 轴)。 球坐标和矩形坐标之间的关系为\(x = r \, \sin \, \theta \, \cos \, \phi\)、\(y = r \, \sin \theta \, \sin \, \phi\)、\(z = r \, \cos \, \theta\)。
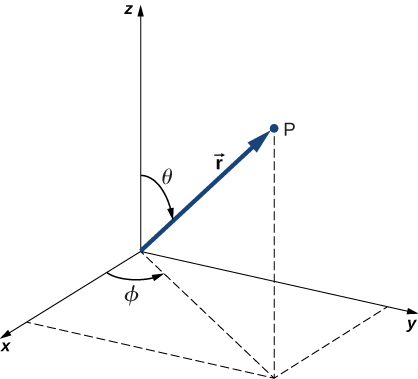
因子\(r \, \sin \, \theta\)是将极向量投影到 xy 平面上所形成的向量的大小。 此外,x 和 y 的坐标是通过将该向量分别投影到 x 轴和 y 轴上来获得的。 逆变换给出
\[\begin{align*} r &= \sqrt{x^2 + y^2 + z^2} \\[4pt] \theta &= \cos^{-1} \left(\frac{z}{r}\right), \\[4pt] \phi &= \cos^{-1} \left( \frac{x}{\sqrt{x^2 + y^2}}\right) \end{align*} \nonumber \]
现代物理学中更高级的课程中讨论了薛定葛在球坐标下氢原子的波动方程,因此我们在这里不详细考虑。 但是,由于的球对称性\(U(r)\),该方程简化为三个更简单的方程:三个坐标(\(r\)\(θ\)、和\(ϕ\))各一个。 与时间无关的波函数的解被写成三个函数的乘积:
\[\psi (r, \theta, \phi) = R(r) \Theta(\theta) \Phi (\phi), \nonumber \]
其中\(R\),径向函数\(r\)仅依赖于径向坐标;\(Θ\)极坐标函数是否仅依赖于极坐标;phi 函数\(θ\)仅依赖于极坐标。\(Φ\)\(ϕ\) 薛定葛方程\(ψ(r, θ, ϕ)\)的有效解由量子数\(n\)\(l\)、和标记\(m\)。
- \(n\): 主量子数
- \(l\): 角动量量子数
- \(m\): 角动量投影量子数
(下一节将解释这些名称的原因。) 径向函数仅\(R\)依赖于\(n\) an\(l\) d;极函数仅\(\Theta\)依赖于 an\(l\) d\(m\);phi 函数仅\(\Phi\)依赖于\(m\)。 每个函数对量子数的依赖用下标表示:
\[\psi_{nlm}(r, \theta, \phi) = R_{nl}(r)\Theta_{lm}(\theta)\Phi_m(\phi). \nonumber \]
并非所有量子数集(\(n\)、\(l\)、\(m\))都是可能的。 例如,轨道角量子数永远\(l\)不能大于或等于主量子数\(n(l < n)\)。 具体来说,我们有
- \(n = 1,2,3,...\)
- \(l = 0,1,2,...,(n-1)\)
- \(m = -l, (-l+1), . . ., 0, . . ., (+l - 1), +l\)
请注意,对于基态,\(n = 1\)\(l = 0\)、和\(m = 0\)。 换句话说,只有一种量子态具有波函数\(n = 1\),而且确实如此\(\psi_{100}\)。 但是,因为\(n = 2\),我们有
\[l = 0, \, m = 0 \nonumber \]
和
\[l = 1, \, m = -1, 0, 1. \nonumber \]
因此,该州允许的\(n = 2\)状态为\(\psi_{200}\)\(\psi_{21-1}\)、\(\psi_{210}\)、和\(\psi_{211}\)。 表中给出了氢原子的波函数示例\(\PageIndex{1}\)。 请注意,其中一些表达式包含字母\(i\),它表示\(\sqrt{-1}\)。 计算概率时,这些复数不会出现在最终答案中。
| \(n = 1, \, l = 0, \, m_l = 0\) | \(\displaystyle \psi_{100} = \frac{1}{\sqrt{\pi}} \frac{1}{a_0^{3/2}}e^{-r/a_0}\) |
| \(n = 2, \, l = 0, \, m_l = 0\) | \(\displaystyle\psi_{200} = \frac{1}{4\sqrt{2\pi}} \frac{1}{a_0^{3/2}}(2 - \frac{r}{a_0})e^{-r/2a_0}\) |
| \(n = 2, \, l = 1, \, m_l = -1\) | \(\displaystyle\psi_{21-1} = \frac{1}{8\sqrt{\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\sin \, \theta e^{-i\phi}\) |
| \(n = 2, \, l = 1, \, m_l = 0\) | \( \displaystyle \psi_{210} = \frac{1}{4\sqrt{2\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\cos \, \theta\) |
| \(n = 2, \, l = 1, \, m_l = 1\) | \( \displaystyle\psi_{211} = \frac{1}{8\sqrt{\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\sin \, \theta e^{i\phi}\) |
量子数的物理意义
氢原子 (\(n\),\(l\),\(m\)) 的三个量子数中的每一个都与不同的物理量相关联。
主量子数
主量子数\(n\)与电子的总能量有关\(E_n\)。 根据薛定的方程式:
\[E_n = - \left(\frac{m_ek^2e^4}{2\hbar^2}\right)\left(\frac{1}{n^2}\right) = - E_0 \left(\frac{1}{n^2}\right), \label{8.3} \]
哪里\(E_0 = -13.6 \, eV\)。 请注意,此表达式与玻尔模型的表达式相同。 与玻尔模型一样,处于特定能量状态的电子不会辐射。
对于氢原子,有多少可能的量子态对应于主数\(n = 3\)? 这些国家的能量是什么?
策略
对于给定能量的氢原子,允许的状态数量取决于其轨道角动量。 我们可以计算主量子数的每个值的这些状态\(n = 1,2,3\)。 但是,总能量仅取决于主量子数,这意味着我们可以使用方程\ ref {8.3} 和计算的状态数。
解决方案
如果\(n = 3\),允许的值\(l\)为 0、1 和 2。 如果\(l = 0\),\(m = 0\)(1 个州)。 如果\(l = 1\),\(m = -1, 0, 1\)(3 个状态);以及 if\(l = 2\),\(m = -2, -1, 0, 1, 2\)(5 个状态)。 总共有 1 + 3 + 5 = 9 个允许的状态。 因为总能量仅取决于主量子数\(n = 3\),所以每种态的能量都是
\[E_{n3} = -E_0 \left(\frac{1}{n^2}\right) = \frac{-13.6 \, eV}{9} = - 1.51 \, eV. \nonumber \]
意义
氢原子中的电子可以以完全相同的能量占据许多不同的角动量态。 随着轨道角动量的增加,允许具有相同能量的状态的数量也会增加。
角动量轨道量子数
角动量轨道量子数\(l\)与氢原子中电子的轨道角动量有关。 量子理论告诉我们,当氢原子处于状态时\(\psi_{nlm}\),其轨道角动量的大小为
\[L = \sqrt{l(l + 1)}\hbar, \nonumber \]
哪里\(l = 0, 1, 2, . . . , (n - 1)\)。
这个结果与玻尔理论的结果略有不同,玻尔理论根据规则量化角动量\(L = n\),其中\(n = 1,2,3, ...\)
使用光谱表示法区分具有不同轨道角动量值的量子态(表\(\PageIndex{2}\))。 s、p、d 和 f 的名称源于早期历史上对原子光谱线进行分类的尝试。 (字母分别代表锋利、主字母、漫反射字母和基本字母。) f 之后,字母按字母顺序继续。
氢气的基态被指定为 1 s 状态,其中 “1” 表示能量水平 (\(n = 1\)),“s” 表示轨道角动量状态 (\(l = 0\))。 W\(n = 2\) h\(l\) en,可以是 0 或 1。 \(n = 2\),\(l = 0\)状态被指定为 “2 s”。 \(n = 2\),\(l = 1\)状态被指定为 “2 p”。 Wh\(l\) en\(n = 3\),可以是 0、1 或 2,状态分别为 3 s、3 p 和 3 d。 表中给出了其他量子态的表示法\(\PageIndex{3}\)。
| 轨道量子数\(l\) | 角动量 | 州 | 光谱名称 |
|---|---|---|---|
| \ (l\)” >0 | 0 | s | 夏普 |
| \ (l\)” >1 | \(\sqrt{2}h\) | p | 校长 |
| \ (l\)” >2 | \(\sqrt{6}h\) | d | 漫反射 |
| \ (l\)” >3 | \(\sqrt{12}h\) | f | 基本面 |
| \ (l\)” >4 | \(\sqrt{20}h\) | g | |
| \ (l\)” >5 | \(\sqrt{30}h\) | h |
角动量投影量子数
角动量投影量子数\(m\)与方位角有关\(\phi\)(见图\(\PageIndex{2}\)),与氢原子中电子轨道角动量的 z 分量有关。 这个组件由下式给出
\[L_z = m\hbar, \nonumber \]
哪里\(m = -l, -l + 1, ..., 0, ..., +l - 1, l\)。
角动量的 z 分量与角动量的大小有关
\[L_z = L \, \cos \theta, \nonumber \]
其中,\(\theta\)是角动量矢量和 z 轴之间的角度。 请注意,z 轴的方向由实验确定,也就是说,在任何方向上,实验者都决定测量角动量。 例如,z 方向可能对应于外部磁场的方向。 \(L_z\)和\(L\)之间的关系如图所示\(\PageIndex{3}\)。
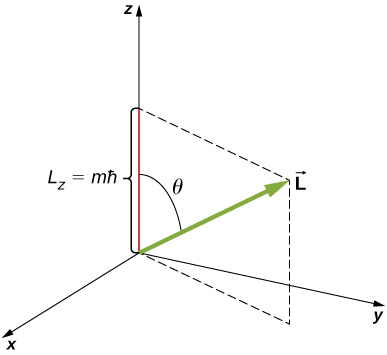
| \(l = 0\) | \(l = 1\) | \(l = 2\) | \(l = 3\) | \(l = 4\) | \(l = 5\) | |
| \(n = 1\) | 1 秒 | |||||
| \(n = 2\) | 2 s | 2 p | ||||
| \(n = 3\) | 3 s | 3 p | 3 d | |||
| \(n = 4\) | 4 s | 4 p | 4 d | 4 f | ||
| \(n = 5\) | 5 s | 5 p | 5 d | 5 f | 5 g | |
| \(n = 6\) | 6 s | 6 p | 6 d | 6 f | 6 g | 6 小时 |
的量化等同\(L_z\)于的量化\(\theta\)。 将 f\(\sqrt{l(l + 1)}\hbar\) or\(L\) 和 f\(m\) or 替换\(L_z\)到这个方程中,我们发现
\[m\hbar = \sqrt{l(l + 1)}\hbar \, \cos \, \theta. \nonumber \]
因此,使用特定\(\theta\)值量化角度
\[\theta = \cos^{-1}\left(\frac{m}{\sqrt{l(l + 1)}}\right). \nonumber \]
请注意,极角 (\(θ\)) 和角动量矢量在任意 z 轴 (\(L_z\)) 上的投影()都是量化的。
\(l = 3\)状态极角的量化如图所示\(\PageIndex{4}\)。 轨道角动量矢量位于圆锥表面的某个地方\(m = 0\),其开口角\(\theta\)相对于 z 轴(除非在这种情况下\(θ = 90^o\)和向量点垂直于 z 轴)。
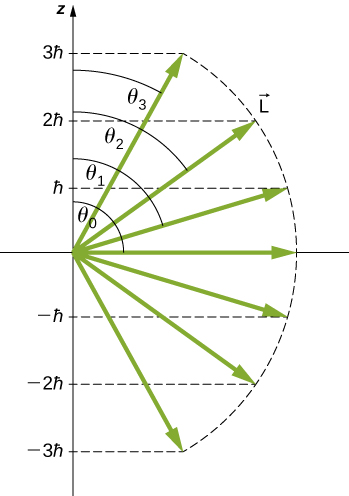
对角动量的详细研究表明,我们无法同时知道所有三个分量。 在上一节中,轨道角动量的 z 分量具有取决于量子数的确定值\(m\)。 这意味着我们无法同时知道角动量的 x 和 y 分量\(L_y\),\(L_x\)而且可以肯定。 因此,轨道角动量矢量的精确方向是未知的。
计算角动量矢量使用 z 轴\(\vec{L}\)可以形成的角度\(l = 1\),如图所示\(\PageIndex{5}\)。
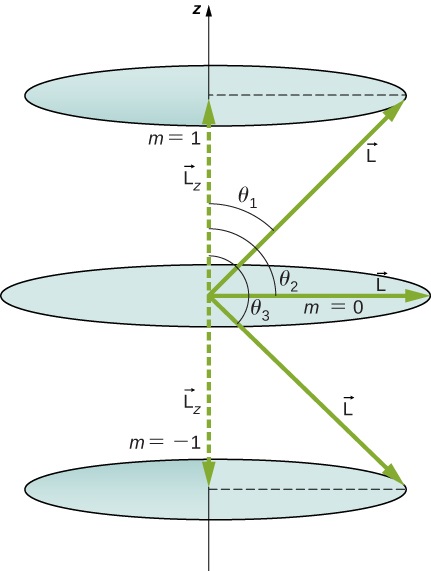
策略
向量\(\vec{L}\)和\(\vec{L_z}\)(在 z 方向)形成直角三角形,其中\(\vec{L}\)是斜边,\(\vec{L_z}\)是相邻边。 与 |\(\vec{L}\) |\(L_z\) 的比率是目标角的余弦值。 大小\(L = |\vec{L}|\)和由下\(L_z\)式给出
\[L = \sqrt{l(l + 1)} \hbar \nonumber \]
和
\[L_z = m\hbar. \nonumber \]
解决方案
我们是给定的\(l = 1\),所以\(m\)可以是 +1、0 或 +1。 因此,\(L\)其值由下式给出
\[L = \sqrt{l(l + 1)}\hbar = \sqrt{2}\hbar. \nonumber \]
该数量\(L_z\)可以有三个值,由给出\(L_z = m_l\hbar\)。
\[L_z = \begin{cases} \hbar, & \text{if } m_l=+1 \\ 0, & \text{if } m_l=0 \\ \hbar, & \text{if } m_l=-1 \end{cases} \nonumber \]
如你在图中所见\(\PageIndex{5}\)\(\cosθ=Lz/L\),所以\(m=+1\),我们有
\[\cos \, \theta_1 = \frac{L_z}{L} = \frac{\hbar}{\sqrt{2}\hbar} = \frac{1}{\sqrt{2}} = 0.707 \nonumber \]
因此,
\[\theta_1 = \cos^{-1}0.707 = 45.0°. \nonumber \]
同样,因为\(m = 0\),我们发现\(\cos \, \theta_2 = 0\);这给出了
\[\theta_2 = \cos^{-1}0 = 90.0°. \nonumber \]
然后对于\(m_l = -1\):
\[\cos \, \theta_3 = \frac{L_Z}{L} = \frac{-\hbar}{\sqrt{2}\hbar} = -\frac{1}{\sqrt{2}} = -0.707, \nonumber \]
所以
\[\theta_3 = \cos^{-1}(-0.707) = 135.0°. \nonumber \]
意义
角度与图形一致。 仅量化相对于 z 轴的角度。 \(L\)只要它与 z 轴成正确的角度,就可以指向任何方向。 因此,如图所示,角动量矢量位于圆锥上。 要了解此处的对应原理如何成立,请考虑最小角度(\(\theta_1\)在示例中)代表最大值\(m_l\),即\(m_l = l\)。 对于那个最小的角度
\[\cos \, \theta = \dfrac{L_z}{L} = \dfrac{l}{\sqrt{l(l + 1)}}, \nonumber \]
当它\(l\)变得非常大时,它接近 1。 如果\(cos \, \theta = 1\),那么\(\theta = 0º\)。 此外,对于大型\(l\),有许多值\(m_l\),因此所有角度都变得可能,因为\(l\)变大了。
这个幅度\(L_z\)能等于\(L\)吗?
- 回答
-
不。 量子数\(m = -l, -l + l, ..., 0, ..., l -1, l\)。 因此,的大小\(L_z\)总是小于\(L\)因为\(<\sqrt{l(l + 1)}\)
使用波浪函数进行预测
正如我们之前所看到的,我们可以使用量子力学通过概率陈述来预测物理事件。 因此,可以说 “此时电子以这种概率位于这个体积内”,但不是 “此时电子位于位置(x、y、z)”。 为了确定在特定空间区域的氢原子中找到电子的概率,有必要在该区域积分概率密度\ (|_ {nlm} |^2) _:
\[\text{Probability} = \int_{volume} |\psi_{nlm}|^2 dV, \nonumber \]
其中\(dV\)是无穷小体积元素。 如果为所有空间计算该积分,则结果为 1,因为粒子位于某处的概率为 100%(归一化条件)。 在关于现代物理学的更高级的课程中,你会发现\(|\psi_{nlm}|^2 = \psi_{nlm}^* \psi_{nlm}\),复杂的共轭物在\(\psi_{nlm}^*\)哪里。 这消除了上述计算\(i = \sqrt{-1}\)中出现的情况。
假设一个处于零角动量状态的电子 (\(l = 0\))。 在这种情况下,电子的波函数仅取决于径向坐标\(r\)。 (请参阅各州\(\psi_{100}\)和表\(\psi_{200}\)中\(\PageIndex{1}\)。) 无穷小体积元素对应于半径\(r\)和无穷小厚度的球壳\(dr\),写为
\[dV = 4\pi r^2dr. \nonumber \]
在 “大约 r” 区域\(r\)\(r + dr\)(“大约 r”)中找到电子的概率为
\[P(r)dr = |\psi_{n00}|^2 4\pi r^2 dr. \nonumber \]
这里\(P(r)\)称为径向概率密度函数(单位长度的概率)。 对于处于氢气基态的电子,在该区域找到电子的概率\(r\)\(r + dr\)为
\[|\psi_{n00}|^2 4\pi r^2 dr = (4/a_)^3)r^2 exp(-2r/a_0)dr, \nonumber \]
哪里\(a_0 = 0.5\) angstroms。 径向概率密\(P(r)\)度函数如图所示\(\PageIndex{6}\)。 任意两个径向位置(比如\(r_1\)和\(r_2\))之间的曲线下方的面积给出了在该径向范围内找到电子的概率。 为了找到最可能的径向位置,我们将该函数的一阶导数设置为零 (\(dP/dr = 0\)) 并求解\(r\)。 最可能的径向位置不等于径向位置的平均值或预期值\(|\psi_{n00}|^2\),因为与其峰值不对称。
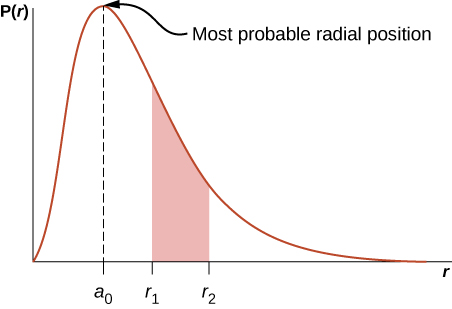
如果电子具有轨道角动量 (\(l \neq 0\)),则代表电子的波函数取决于角度\(\theta\)和\(\phi\);也就是说\(\psi_{nlm} = \psi_{nlm}(r, \theta, \phi)\)。 带有\(n = 2\)和的三个状态的原子轨道如图\(l = 1\)所示\(\PageIndex{7}\)。 原子轨道是空间中包含一定百分比(通常为90%)电子概率的区域。 (有时原子轨道被称为概率的 “云”。) 请注意,这些分布在特定方向上是显著的。 当化学家分析原子如何结合在一起形成分子时,这种方向性很重要。
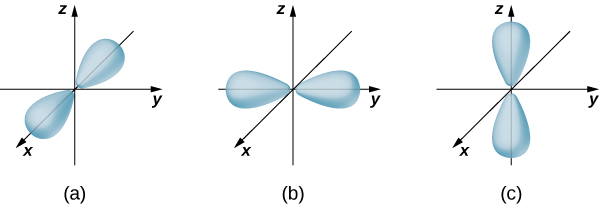
波函数的表示方式略有不同,如图所示\(\PageIndex{8}\)。 在这种情况下,亮区和暗区分别表示概率相对较高和较低的位置。 与玻尔氢原子的模型形成鲜明对比的是,电子不会在明确的路径上绕质子核移动。 事实上,不确定性原理使人们无法知道电子是如何从一个地方到达另一个地方的。