6.7: 波粒二元性
- Page ID
- 202006
在本节结束时,您将能够:
- 识别电磁波表现得像光子束而粒子表现得像波浪的现象
- 描述电子显微镜背后的物理原理
- 总结导致量子力学发展的科学思想的演变
无线电信号接收天线探测到的辐射能量是电磁波的能量。 光电效应中光电流检测到的辐射能量与单个光子粒子的能量相同。 因此,出现了关于电磁辐射本质的问题:光子是波还是粒子? 对于其他已知的能量形式,可能会问类似的问题。 例如,构成电路中电流一部分的电子的行为就像粒子在导体内部与其他电子同步移动。 同一个电子在穿过固体晶体结构并形成衍射图像时表现为波浪。 电子是波还是粒子? 同样的问题可以扩展到所有物质粒子 —— 基本粒子和化合物分子 —— 询问它们的真实物理性质。 在我们目前的知识状态下,关于事物真实本质的这些问题没有确凿的答案。 我们只能说波粒二元性存在于自然界中:在某些实验条件下,粒子似乎起着粒子的作用,而在不同的实验条件下,粒子似乎起着波浪的作用。 相反,在某些物理环境下,电磁辐射充当波浪,而在其他物理环境下,辐射充当光子束。
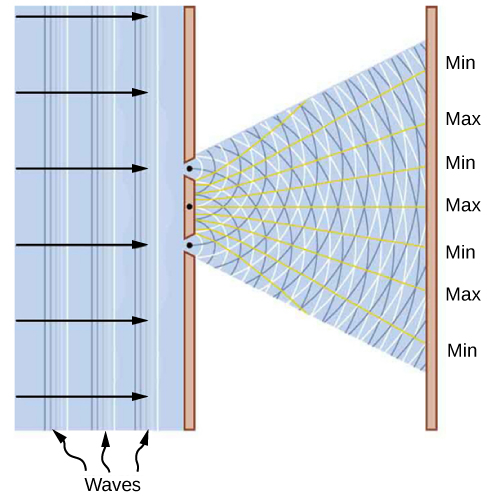
这种二元解释并不是二十世纪特定发现带来的新物理学概念。 从1670年开始,艾萨克·牛顿和克里斯蒂安·惠更斯之间关于光的本质的辩论中就已经出现了这一点。 根据牛顿的说法,光束是光小体的集合。 根据惠更斯的说法,光是一种波浪。 1803 年,Thomas Young 宣布了对光的双缝干扰实验(见图\(\PageIndex{1}\)),该实验牢固地将光确立为波浪,因此微粒假说失败了。 在詹姆斯·克莱克·麦克斯韦的电磁学理论(1873年完成)中,光是一种电磁波。 麦克斯韦将辐射视为电磁波的经典观点在今天仍然有效;但是,它无法解释黑体辐射和光电效应,光充当光子束。
在解释电力时也存在类似的二分法。 从本杰明·富兰克林在 1751 年对电力的观测到 1897 年 J.J. Thomson 发现电子,电流被视为连续电介质中的流动。 在这种电流体理论中,发展了当前的电路理论,并发现了电磁学和电磁感应。 汤姆森的实验表明,负电荷(电子)的单位可以在真空中传播,没有任何介质来携带电荷,就像在电路中一样。 这一发现改变了当今人们理解电力的方式,赋予了电子粒子状态。 在玻尔早期的氢原子量子理论中,电子和质子都是物质粒子。 同样,在康普顿对电子的X射线散射中,电子是一个粒子。 另一方面,在晶体结构的电子散射实验中,电子表现为波浪。
怀疑论者可能会提出一个问题,即电子可能永远只不过是一个粒子,而在电子散射实验中获得的衍射图像可以在晶体的宏观模型和电子像乒乓雨一样冲向它的宏观模型中解释球。 事实上,要研究这个问题,我们不需要复杂的晶体模型,而只需要在屏幕上对电子不透明的几个简单缝隙即可。 换句话说,为了收集有关电子性质的令人信服的证据,我们需要用电子重复杨双缝实验。 如果电子是波,我们应该观察波浪的典型干扰模式的形成,例如图中所描述的干扰模式\(\PageIndex{1}\),即使电子一个接一个地穿过狭缝。 但是,如果电子不是波而是粒子,则不会形成干涉条纹。
克劳斯·延森(Claus Jönsson)于1961年在德国进行的首次电子束双缝实验表明,电子束确实形成了干扰模式,这意味着电子共同表现为波浪。 朱利奥· 波齐(Giulio Pozzi)于1974年在意大利进行了首次双缝实验,1989年由藤村明在日本进行了单电子逐个穿过狭缝的双缝实验。 它们表明,即使电子单独穿过狭缝,干扰条纹也是逐渐形成的。 这最终表明,电子衍射图像的形成是由于电子的波浪性质。 图中干扰模式的图像说明了在电子双缝实验中看到的结果\(\PageIndex{2}\)。

在一个研究电子波干扰模式的实验装置中,在镀金的硅膜中产生了两个狭缝。 每个狭缝的宽度为 62 纳米,长 4 微米,缝隙之间的间隔为 272 nm。 电子束是在电子枪中通过加热钨元素并使电子加速穿过 600 伏电位而产生的。 随后使用电磁透镜对光束进行准直,准直的电子束通过狭缝发送。 在查看屏幕上找到一阶明亮条纹的角度位置。
策略
回想一下,杨的双缝干涉图案(在上一章中讨论过)中形成的第 n 阶亮条纹的角度位置 β 与狭缝之间的分离 d 以及方程 dsin β = nλ中入射光的波长 λ有关,其中 n = 0\(\pm 1\)、\(\pm 2\)、... 给出间隔,等于 d = 272 nm。 对于一阶条纹,我们采用 n = 1。 我们现在唯一需要的是入射电子波的波长。
由于电子已在 ΔV = 600 V 的电位差中从静止状态中加速,因此其动能为 K = e ΔV = 600 eV。 电子的剩余质量能量为\(E_0\) = 511 keV。
我们将它的 de Broglie 波长计算为非相对论电子的波长,因为它的动能 K 比静止能量\(E_0\) K 小得多\(E_0\)。
解决方案
电子的波长是
\[\lambda = \frac{h}{p} = \frac{h}{\sqrt{2m_eK}} = \frac{h}{\sqrt{2E_0/c^2K}} = \frac{hc}{\sqrt{2E_0K}} = \frac{1.241 \times 10^{-6} \, eV \cdot m}{\sqrt{2(511 \, keV)(600 \, eV)}} = 0.050 \, nm. \nonumber \]
此 λ用于获取第一个明亮条纹的位置:
\[\sin \, \theta = \frac{1 \cdot \lambda}{d} = \frac{0.050 \, nm}{272 \, nm} = 0.000184 \Rightarrow θ = 0.010°. \nonumber \]
意义
请注意,这也是两个连续明亮条纹之间的角度分辨率,最高可达大约 n = 1000。 例如,在零阶条纹和一阶条纹之间,在一阶条纹和二阶条纹之间
对于示例中描述的情况\(\PageIndex{1}\),请在查看屏幕上找到五阶明亮条纹的角度位置。
- 回答
-
\(0.052^o\)
物质粒子和辐射的波粒双重性质表明我们无法用一种统一的经典理论来描述物理现实,因为无论是经典的粒子方法还是传统的波浪方法都无法完全解释观测到的现象。 传统方法的这种局限性在1928年得以实现,玻尔、埃德温· 施罗丁格、沃纳· 海森伯格和保罗· 狄拉克为一种名为量子力学的新统计理论奠定了基础。 量子力学将德布罗格利关于物质波的概念视为所有粒子的基本特性,并对其进行了统计学解释。 根据这种解释,与粒子相关的波浪携带有关粒子可能的位置及其其他特性的信息。 单个粒子被视为移动波包,如图所示\(\PageIndex{3}\)。 我们可以从这个例子中直观地感觉到,如果一个粒子是一个波包,我们将无法以同样的意义测量它的确切位置,就像我们无法在振动的吉他弦中精确定位波包的位置一样。 测量粒子位置的不确定度 Δx 与海森堡的不确定度原理同时测量其线性动量时的不确定度 △p 有关:
\[\Delta x \Delta p \geq \frac{1}{2}\hbar. \label{6.63} \]
海森堡的原理表达了自然法则,即在量子层面上,我们的感知是有限的。 例如,如果我们同时知道物体的确切位置(这意味着方程式\ ref {6.63} 中的 Δx = 0),我们就无法知道它的动量,因为那样的话,其动量的不确定性就会变为无穷大(因为方程\ ref {6.63} 中的 △p ≥ 0.5 /αx)。 海森堡不确定性原理为同时测量粒子的位置和动量的精度设定了极限;它表明,我们能获得的最佳精度是当我们在方程\ ref {6.63} 中有等号 (=) 时,即使是最好的,我们也无法做得比这更好未来的工具。 海森堡的原理是粒子的波浪性质的结果。

我们经常使用许多利用波粒二元性的电子设备,甚至没有意识到其操作背后的物理学的复杂性。 基于光子和电子粒子特性的技术的一个例子是电荷耦合器件,它用于任何需要高质量数字数据的仪器中的光检测,例如在数码相机或医疗传感器中。 利用电子波特性的一个例子是电子显微镜。
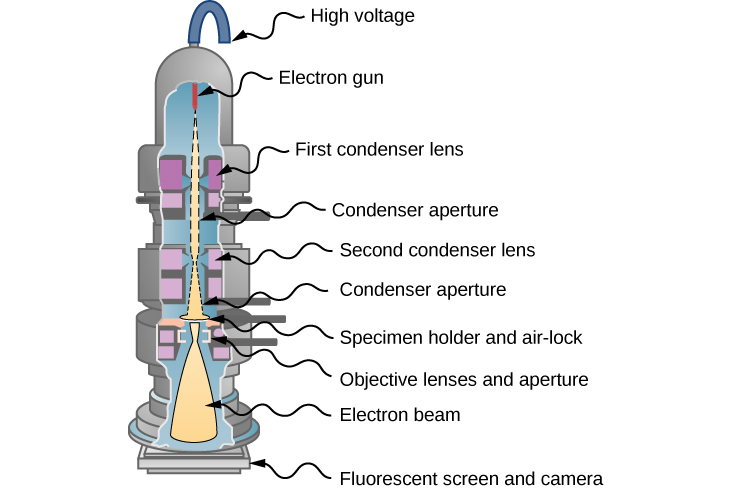
1931年,物理学家恩斯特·鲁斯卡(Ernst Ruska)基于磁场可以引导电子束的思想,开发了电子显微镜的第一个原型,就像透镜可以引导光学显微镜中的光束一样。 这种发展起源于电子显微镜领域。 如图所示,在透射电子显微镜(TEM)中\(\PageIndex{4}\),电子由热钨元素产生,并由电子枪中的电位差加速,这使它们的动能高达400 keV。 离开电子枪后,电子束由电磁透镜(一种聚光透镜系统)聚焦,然后通过样本样本进行观察。 样品的图像由透射的电子束重建而成。 放大的图像可以直接在荧光屏幕上观看,也可以通过将其发送到数码相机或计算机显示器等方式间接观看。 由电子枪、镜头、标本和荧光屏组成的整个装置都封闭在真空室中,以防止光束的能量损失。 透射电镜的分辨率仅受球面像差的限制(已在前一章中讨论)。 现代高分辨率透射电镜模型的分辨率可以大于 0.5 Ω,放大倍率可以高于 5000 万倍。 相比之下,使用光学显微镜获得的最佳分辨率目前约为97 nm。 透射电镜的一个局限性是样品的厚度必须约为100纳米,生物样品需要一种涉及化学 “固定” 的特殊制剂来稳定它们以进行超薄切片。
这种限制在曼弗雷德·冯·阿登纳于1937年发明的扫描电子显微镜(SEM)中没有出现。 在 SEM 中,电子束的典型能量高达 40 keV,电子束不是通过样品传输,而是从其表面散射。 样品的表面形貌是通过分析反向散射电子、透射电子以及电子与样品中的原子相互作用产生的发射辐射来重建的。 SEM 的分辨率优于 1 nm,放大倍率比使用光学显微镜获得的放大倍率高 250 倍以上。 扫描电镜扫描的样品可以长达几厘米,但必须根据样品的电学特性进行特殊制备。
透射电镜和扫描电镜的高放大倍率使我们能够看到单个分子。 透射电镜和扫描电镜的高分辨率使我们能够看到精细的细节,例如本章开头的花粉扫描电镜显微照片中显示的细节(图6.1.1)。
如果 TEM 的下午 1 点 0 分的电子束穿过 2.0 微米的圆形开口,那么这款显微镜的两个刚刚可分辨的点源之间的角度是多少?
解决方案
当入射辐射的波长为\(λ=1.0\, pm\)且孔径直径为时\(Δθ\),我们可以直接使用显微镜的分辨率公式来计算显微镜的分辨力\(D = 2.0\, μm\):
\[\Delta \theta = 1.22 \frac{\lambda}{D} = 1.22 \frac{1.0 \, pm}{2.0 \, \mu m} = 6.10 \times 10^{-7} rad = 3.50 \times 10.5^o. \nonumber \]
意义
请注意,如果我们使用具有 400 纳米光的传统显微镜,则分辨率将仅为 14°,这意味着图像中的所有精细细节都将变得模糊。
假设示例中孔径的直\(\PageIndex{2}\)径减半。 它如何影响决心力?
- 回答
-
把它加倍


