6.6: De Broglie 的 Matter Waves
- Page ID
- 202026
在本节结束时,您将能够:
- 描述 de Broglie 关于物质波的假设
- 解释一下 de Broglie 的假设是如何为玻尔氢原子量子理论中角动量量化提供理由的
- 描述 Davisson—Germer 实验
- 解释 de Broglie 对物质波的看法以及它们如何解释电子衍射现象
康普顿的公式确定,电磁波在与物质相互作用时可以表现得像光粒子。 1924年,路易斯· 德·布罗格利提出了一个新的推测假设,即电子和其他物质粒子的行为可以像波浪一样。 今天,这个想法被称为德布罗格利关于物质波的假设。 1926年,德布罗格利的假设以及玻尔早期的量子理论促成了一种描述原子和亚原子粒子物理学的新波量子力学理论的发展。 量子力学为新的工程发明和技术铺平了道路,例如激光和磁共振成像(MRI)。 这些新技术推动了生物学和化学等其他科学的发现。
根据德布罗格利的假设,无质量光子和大粒子必须满足一组常见的关系,将能量\(E\)与频率联系起来\(f\),将线性动量\(p\)与波长联系起来\(λ\)。 我们已经在康普顿效应的背景下讨论了光子的这些关系。 我们现在是在更广泛的背景下回顾它们。 任何具有能量和动量的粒子都是频率\(f\)和波长的 de Broglie 波\(\lambda\):
\[ E = h f \label{6.53} \]
\[ \lambda = \frac{h}{p} \label{6.54} \]
这里\(E\)和分别\(p\)是相对论能量和粒子的动量。 De Broglie 的关系通常用波向量\(\vec{k}\)和波频来表示\(\omega = 2 \pi f\),就像我们通常对波浪所做的那样:\(k = 2 \pi / \lambda\)
\ begin {aligned}
&E=\ hbar\ omega\ label {6.55}\\
&\ vec {p} =\ hbar\ vec {k}\ label {6.56}
\ end {aligned}
波浪理论告诉我们,波浪随群速度携带能量。 对于物质波,该群速度是粒\(u\)子的速度。 分别用相对论能量和相对论动量来识别粒子的能量 E\(mc^2\) 和动量 p\(mu\),可以得出德布罗格利关系得出的结论是物质波满足以下关系:
\[ \lambda f =\frac{\omega}{k}=\frac{E / \hbar}{p / \hbar}=\frac{E}{p} = \frac{m c^{2}}{m u}=\frac{c^{2}}{u}=\frac{c}{\beta} \label{6.57} \]
哪里\(\beta = u/c\)。 当粒子无质量时,我们就有了\(u=c\)方程\ ref {6.57}\(\lambda f = c\)。
计算 de Broglie 的波长:
- 以 10 m/s 的速度投出 0.65 千克的篮球,
- 动能为 1.0 eV 的非相对论电子,以及
- 一种动能为 108 keV 的相对论电子。
策略
我们使用方程\ ref {6.57} 来找出 de Broglie 波长。 当问题涉及非相对论物体以非相对论速度 u 移动时,比如 in (a) when\(\beta=u / c \ll 1\),我们使用非相对论动量 p。 当无法使用非相对论近似值时,例如在 (c) 中,我们必须使用相对论动量\(p=m u=m_{0} \gamma u=E_{0} \gamma \beta/c\),其中粒子的剩余质量能\(\gamma\)是洛伦兹因子\(\gamma=1 / \sqrt{1-\beta^{2}}\)。\(E_0 = m c^2 \) 粒子的总能量\(E\)由方程\ ref {6.53} 给出,动能为\(K=E-E_{0}=(\gamma-1) E_{0}\)。 当知道动能时,我们可以反转方程 6.4.2 来找到动量
\[ p=\sqrt{\left(E^{2}-E_{0}^{2}\right) / c^{2}}=\sqrt{K\left(K+2 E_{0}\right)} / c \nonumber \]
然后用方程式\ ref {6.57} 代替
\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}} \label{6.58} \]
根据当前的问题,在这个方程中,我们可以为 hc 使用以下值:
\[ h c=\left(6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)=1.986 \times 10^{-25} \: \mathrm{J} \cdot \mathrm{m}=1.241 \: \mathrm{eV} \cdot \mu \mathrm{m} \nonumber \]
解决方案
- 对于篮球来说,动能是\[ K=m u^{2} / 2=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})^{2} / 2=32.5 \: \mathrm{J} \nonumber \],其余的质量能是\[ E_{0}=m c^{2}=(0.65 \: \mathrm{kg})\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)^{2}=5.84 \times 10^{16} \: \mathrm{J} \nonumber \]我们看见了\(K /\left(K+E_{0}\right) \ll 1\)然后使用\(p=m u=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})=6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m} \):\[ \lambda=\frac{h}{p}=\frac{6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}}{6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m}}=1.02 \times 10^{-34} \: \mathrm{m} \nonumber \]
- 对于非相对论电子,\[ E_{0}=mc^{2}=\left(9.109 \times 10^{-31} \mathrm{kg}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)^{2}=511 \mathrm{keV} \nonumber \]以及何时\(K = 1.0 \: eV\)有\(K/(K+E_0) = (1/512) \times 10^{-3} \ll 1\),所以我们可以使用非相对论公式。 但是,这里使用方程\ ref {6.58} 要简单一些:\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{(1.0 \: \mathrm{eV})[1.0 \: \mathrm{eV}+2(511 \: \mathrm{keV})]}}=1.23 \: \mathrm{nm} \nonumber \]如果我们使用非相对论动量,则会得到相同的结果,因为 1 eV 比电子的剩余质量小得多。
- 对于快速电子来说\(K=108 \: keV\),相对论效应不容忽视,因为它的总能量\(K/E = 108/619\)是\(E = K = E_0 = 108 \: keV + 511 \: keV = 619 \: keV\)而且不可忽略的:\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{108 \: \mathrm{keV}[108 \: \mathrm{keV}+2(511 \: \mathrm{keV})]}}=3.55 \: \mathrm{pm} \nonumber \].
意义
从这些估计中我们可以看出,De Broglie 的宏观物体(例如球)的波长非常小。 因此,即使它们存在,它们也无法被检测到,也不会影响宏观物体的运动。
德布罗格利动能为 1.0 eV 的非相对论质子的波长是多少?
- 回答
-
下午 1.7 点
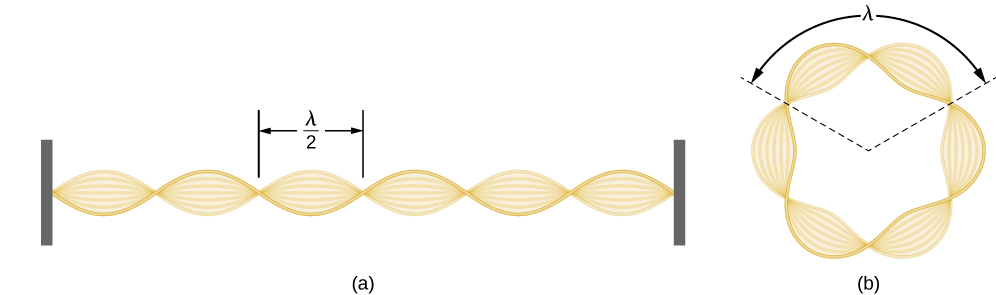
德布罗格利使用电子物质波的概念,为量化氢原子中电子的角动量提供了理由,玻尔的量子理论对此进行了假设。 当我们假设氢原子中的电子行为不像粒子而是波浪时,第一个玻尔量化条件的物理解释自然而然地出现了。 为了清楚地看到它,想象一下,一根拉伸的吉他弦被夹在两端,并在其普通模式下振动。 如果弦的长度为 l(图\(\PageIndex{1}\)),则这些振动的波长不能是任意的,但必须使整数 k 的半波长精确\(\lambda/2\)匹配两者之间的距离 l结束。 这是在弦上出现驻波的条件\(l=k \lambda /2\)。 现在假设我们没有将绳子夹在墙上,而是将其长度弯曲成一个圆圈,然后将其两端相互固定。 这会产生一个在普通模式下振动的圆串,满足相同的驻波条件,但是现在半波长的数量必须是偶数\(k\)\(k=2n\),长度 l 现在与圆\(r_n\)的半径相连。 这意味着半径不是任意的,但必须满足以下驻波条件:
\[ 2 \pi r_{n}=2 n \frac{\lambda}{2} \label{6.59}. \]
如果第 n 个玻尔轨道上的电子以波浪形式移动,则根据方程\ ref {6.59},其波长必须等于\(\lambda = 2 \pi r_n / n\)。 假设方程\ ref {6.58} 有效,则该波长的电子波对应于电子的线性动量\(p = h/\lambda = nh / (2 \pi r_n) = n \hbar /r_n\)。 因此,在圆形轨道上,电子的角动量必须为
\[ L_{n}=r_{n} p=r_{n} \frac{n \hbar}{r_{n}}=n \hbar \label{6.60} . \]
该方程是玻尔的第一个量化条件,由方程 6.5.6 给出。 为玻尔的量化条件提供物理解释是物质波存在的令人信服的理论论依据。
找出处于氢气基态的电子的 de Broglie 波长。
策略
我们将方程\ ref {6.60} 中的第一个量化条件与方程 6.5.6 相结合,并使用方程 6.5.9 作为第一个玻尔半径\(n = 1\)。
解决方案
何时\(n=1\)和\(r_n = a_0 = 0.529 \: Å\),玻尔量化条件给出\(a_{0} p=1 \cdot \hbar \Rightarrow p=\hbar / a_{0}\)。 电子波长为:
\[ \lambda=h / p = h / \hbar / a_{0} = 2 \pi a_{0} = 2 \pi(0.529 \: Å)=3.324 \: Å .\nonumber \]
意义
当我们直接使用方程式\ ref {6.58} 时,我们会得到相同的结果。
找出处于氢气第三激发态的电子的 de Broglie 波长。
- 回答
-
\(\lambda = 2 \pi n a_0 = 2 (3.324 \: Å) = 6.648 \: Å\)
1927 年,C. Davisson 和 L. Germer 进行了一系列电子散射实验,清楚地表明电子的行为确实像波浪,对物质波进行了实验证实。 戴维森和格默没有进行实验来证实德布罗格利的假设:这一确认是他们对受到电子轰击的金属表面进行常规实验研究的副产品。
在提供电子波第一个证据的特定实验(今天称为戴维森-格默实验)中,他们研究了镍的表面。 他们的镍样品是在高温烤箱中专门制备的,目的是将其通常的多晶结构转变为大型单晶域占据体积的形式。 图中\(\PageIndex{2}\)显示了实验设置。 热电子从电子枪中的加热元件(通常由钨制成)中释放出来,然后通过电位差 ΔV 加速,变成由电子枪产生的准直良好的电子束。 通过选择电子枪\(K\)中电位差的值来调整电子的动能。 根据能量守恒原则,这会产生一束具有设定线性动量值的电子束:
\[ e \Delta V=K=\frac{p^{2}}{2 m} \Rightarrow p=\sqrt{2 m e \Delta V} \label{6.61} \]
电子束沿着垂直于其表面的方向入射到镍样品上。 在表面,它向不同方向散射。 在选定方向上散射的光束的强度由高度灵敏的探测器测量。 探测器相对于入射光束方向的角度位置可以在 pp=0° 到 pp=90° 之间变化。 整个装置都封闭在真空室中,以防止电子与空气分子碰撞,因为这种热碰撞会改变电子的动能,是不可取的。
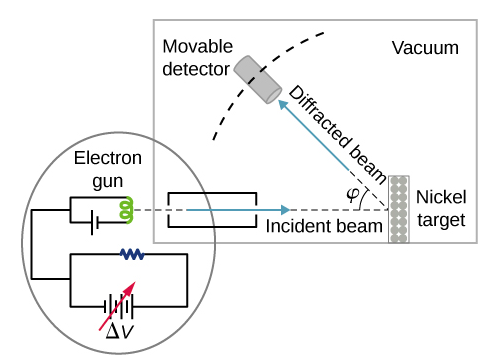
当镍靶呈多晶形态,有许多随机定向的微观晶体时,入射电子会从其表面向不同的随机方向散射。 因此,散射电子束的强度在任何方向上都大致相同,类似于来自多孔表面的光的漫反射。 但是,当镍靶具有规则的晶体结构时,散射电子束的强度在特定角度显示出明显的最大值,结果显示出清晰的衍射图案(见图\(\PageIndex{3}\))。 父子物理学家威廉·布拉格和威廉·布拉格在1912年研究了由各种晶体固体散射的X射线形成的类似衍射图案。 X 射线晶体学中的布拉格定律提供了入射到晶格上的辐射波长\(\lambda\)、晶格间距和衍射辐射中干扰最大值的位置之间的联系(参见衍射)。
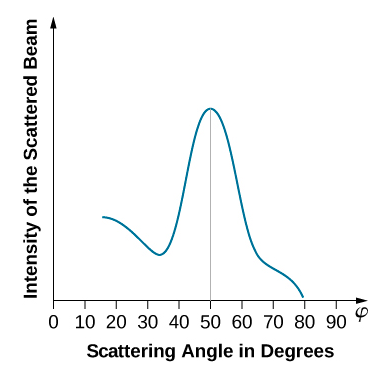
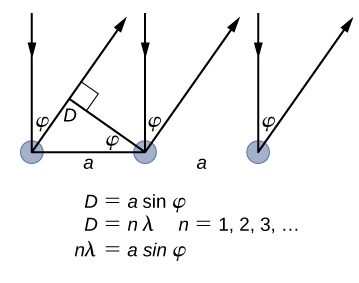
使用 X 射线晶体学确定的戴维森-格默目标的晶格间距被测定为\(a=2.15 \: Å\)。 与 X 射线穿透样品的 X 射线晶体学不同,在最初的 Davisson—Germer 实验中,只有表面原子与入射电子束相互作用。 对于表面衍射,对于满足 nl = a sin phi 条件的散射角度,可以观察到反射电子束的最大强度(见图\(\PageIndex{4}\))。 一阶最大值(对于 n=1)是在 △V54 V 处以 α~50° 的散射角测量的,这使得入射辐射的波长为 λ= (2.15 Ω) sin 50° = 1.64 Å。 另一方面,54 V 的电位将入射电子加速至 K = 54 eV 的动能。 根据方程\ ref {6.61} 计算得出的它们的动量为\(p = 2.478 \times 10^{−5} \: eV \cdot s/m\)。 当我们在方程式\ ref {6.58} 中替换这个结果时,de Broglie 波长得出为
\[ \lambda=\frac{h}{p}=\frac{4.136 \times 10^{-15} \mathrm{eV} \cdot \mathrm{s}}{2.478 \times 10^{-5} \mathrm{eV} \cdot \mathrm{s} / \mathrm{m}}=1.67 \mathrm{Å} \label{6.62}. \]
当我们在方程式\ ref {6.61} 中使用 K = 54eV 时,也会得到相同的结果。 这个理论结果与戴维森—Germer实验值 λ= 1.64 Å接近,这是德布罗格利物质波存在的令人信服的论据。
使用低能电子测量的衍射线,例如戴维森—格默实验中使用的衍射线,相当宽泛(图\(\PageIndex{3}\)),因为入射电子只能从表面散射。 当更高能量的电子束穿过薄金属箔时,衍射图像的分辨率会大大提高。 之所以出现这种情况,是因为衍射图像是通过从体积内的许多晶体平面散射而产生的,而在布拉格角散射中产生的最大值非常清晰(图\(\PageIndex{5}\))。

自从戴维森和格默工作以来,德布罗格利的假设已经通过各种实验技术进行了广泛的检验,许多基本粒子都证实了德布罗格利波的存在。 中子已被用于散射实验,以根据中子物质波形成的干扰模式确定固体的晶体结构。 中子的电荷为零,其质量与带正电荷的质子的质量相当。 中子和质子都可以看作是物质波。 因此,物质波的特性并不是带电粒子所特有的,而是运动中的所有粒子所特有的。 已经测量了像碳一样大的分子\(C_{60}\)的物质波。 所有物理物体,无论大小,只要它们保持运动状态,都会产生相关的物质波。 de Broglie 物质波的普遍特征已经牢固确立。
假设在典型晶体固体的衍射实验中使用了中子束。 估计中子束中子(以 eV 为单位)的动能,并将其与室温下处于平衡状态的理想气体的动能进行比较。
策略
我们假设典型的晶体间距 a 约为 1.0 Ω。 要观察这种晶格上的衍射图案,中子波长 β 必须与晶格间距处于相同的数量级。 我们使用方程\ ref {6.61} 来求动量 p 和动能 K。 为了将这种能量与室温下处于平衡状态的理想气体的能\(E_T\)量进行比较\(T = 300 \, K\),我们使用关系\(K = 3/2 k_BT\),其中\(k_B = 8.62 \times 10^{-5}eV/K\)是玻尔兹曼常数。
解决方案
我们评估 pc 以将其与中子的剩余质量能量进行比较\(E_0 = 940 \, MeV\):
\[p = \frac{h}{\lambda} \Rightarrow pc = \frac{hc}{\lambda} = \frac{1.241 \times 10^{-6}eV \cdot m}{10^{-10}m} = 12.41 \, keV. \nonumber \]
我们看到\(p^2c^2 << E_0^2\)了这一点,我们可以使用非相对论的动能:
\[K = \frac{p^2}{2m_n} = \frac{h^2}{2\lambda^2 m_n} = \frac{(6.63\times 10^{−34}J \cdot s)^2}{(2\times 10^{−20}m^2)(1.66 \times 10^{−27} kg)} = 1.32 \times 10^{−20} J = 82.7 \, meV. \nonumber \]
在 300 K 时处于平衡状态的理想气体的动能为:
\[K_T = \frac{3}{2}k_BT = \frac{3}{2} (8.62 \times 10^{-5}eV/K)(300 \, K) = 38.8 \, MeV. \nonumber \]
我们看到这些能量具有相同的数量级。
意义
能量在此范围内的中子被称为 “热中子”,这是室温下理想气体的典型特征。
在欧洲核子研究组织的超级对撞机中,质子可以加速到0.75 摄氏度的速度。 在这种速度下,它们的 de Broglie 波长是多少? 他们的动能是多少?
策略
质子的剩余质量能量是\(E_0 = m_0c^2 = (1.672 \times 10^{−27} kg)(2.998 \times 10^8m/s)^2 = 938 \, MeV\)。 当质子的速度已知时,我们得到 β = 0.75 和\(\beta \gamma = 0.75 / \sqrt{1 - 0.75^2} = 1.714\). 我们从相对论关系中获得波长 λ和动能 K。
解决方案
\[\lambda = \frac{h}{p} = \frac{hc}{\beta \gamma E_0} = \frac{1.241 \, eV \cdot \mu m}{1.714 (938 \, MeV)} = 0.77 \, fm \nonumber \]
\[K = E_0(\gamma - 1) = 938 \, MeV (1 /\sqrt{1 - 0.75^2} - 1) = 480.1\, MeV \nonumber \]
意义
请注意,由于质子的质量是电子的1835倍,因此如果用电子进行这个实验,那么简单地重新调整这些结果就可以得出电子的波长为 (1835) 0.77 fm = 1.4 pm,其动能为480.1 meV /1835 = 261.6 keV。
找出以 0.75 c 速度传播的自由电子的 de Broglie 波长和动能。
- 回答
-
\(\lambda = 1.417 \, pm; \, K = 261.56 \, keV\)


