6.5: 玻尔的氢原子模型
- Page ID
- 202013
在本节结束时,您将能够:
- 解释原子发射的辐射的吸收光谱和发射光谱之间的区别
- 描述卢瑟福金箔实验和原子核的发现
- 解释氢的原子结构
- 描述早期量子理论对氢原子的假设
- 总结一下玻尔的氢原子的量子模型如何解释原子氢的辐射光谱
从历史上看,玻尔的氢原子模型是第一个正确解释原子氢辐射光谱的原子结构模型。 该模型在物理学史上占有特殊的地位,因为它引入了早期的量子理论,它带来了科学思想的新发展,后来又导致了量子力学的发展。 要了解玻尔模型的细节,我们必须首先回顾十九世纪促成其形成的发现。
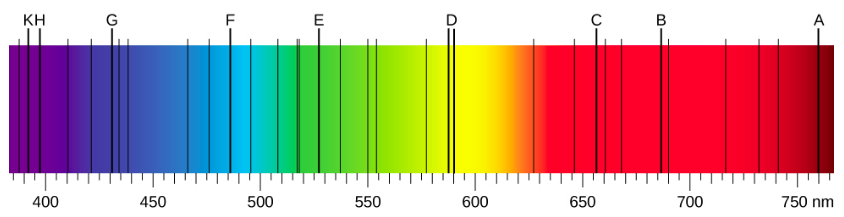
当我们使用棱镜分析来自太阳的白光时,可以观察到太阳光谱中的几条黑线(图\(\PageIndex{1}\))。 太阳吸收线以约瑟夫·冯· 弗劳恩霍夫的名字被称为弗劳恩霍夫线,他精确测量了它们的波长。 在1854—1861年期间,古斯塔夫·基尔霍夫和罗伯特·本森发现,对于各种化学元素,元素的线发射光谱与其线吸收光谱完全匹配。 图中解释了吸收光谱和发射光谱之间的区别\(\PageIndex{2}\)。
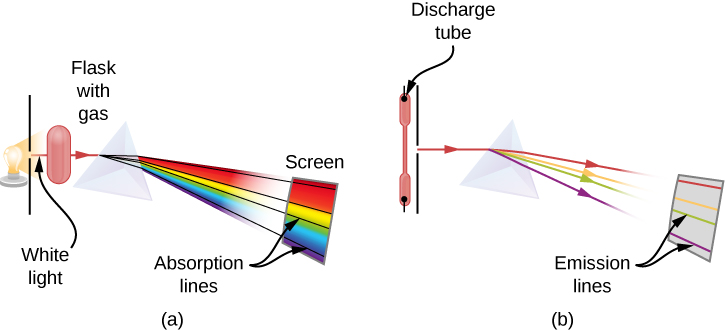
当光线穿过气体时,可以观察到吸收光谱。 该光谱显示为黑线,仅出现在白光连续光谱背景上的某些波长(图\(\PageIndex{2}\))。 缺失的波长告诉我们哪些波长的辐射被气体吸收。 当气体发射光时,可以观察到发射光谱。 该光谱被视为黑色背景上的彩色线条(图\(\PageIndex{3}\)和\(\PageIndex{4}\))。 发射线的位置告诉我们哪些波长的辐射是由气体发射的。 每种化学元素都有自己的特性发射光谱。 对于每个元素,其发射线的位置与其吸收线的位置完全相同。 这意味着特定元素的原子只能吸收特定波长的辐射,而没有这些波长的辐射根本不会被元素吸收。 这也意味着每个元素的原子发射的辐射的波长与它们吸收的辐射的波长完全相同。


元素的发射光谱具有复杂的结构;对于原子序数较高的元素,它们变得更加复杂。 如图所示\(\PageIndex{4}\),最简单的光谱属于氢原子。 人眼只能看到四条线。 在图中从右至左读取时\(\PageIndex{4}\),这些线条是:红色(656 nm),称为\(H-\alpha\)直线;浅绿色(486 nm)、蓝色(434 nm)和紫罗兰色(410 nm)。 波长小于 400 nm 的线条出现在光谱的紫外线部分(图\(\PageIndex{4}\),最左边),人眼看不见。 该系列中有无限多的氢气不可见光谱线。
1885 年,约翰· 巴尔默发现了一个描述该系列氢气发射线位置(波长)的经验公式。 它被称为 Balmer 配方:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{n^2}\right). \label{balmer} \]
该常数\(R_H = 1.09737 \times 10^7 m^{-1}\)被称为氢气的里德伯格常数。 在方程\ ref {balmer} 中,正整数 n\(n = 3, 4,5,6\) 取该系列中四条可见线的值。 由巴尔默公式给出的系列氢气发射线称为巴尔默系列。 里德伯格公式描述了二十世纪发现的其他氢气排放线,该公式总结了所有实验数据:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right)\label{rydberg} \]
其中\(n_i = n_f > n_i\)(以整数为单位)。
当时\(n_f = 1\),该系列光谱线被称为莱曼系列。 当时\(n_f = 2\),该系列被称为巴尔默系列,在这种情况下,里德伯格公式与巴尔默公式(方程\ ref {balmer})一致。 何时\(n_f = 3\),该系列被称为 Paschen 系列。 何时\(n_f = 4\),该系列被称为 Brackett 系列。 何时\(n_f = 5\),该系列被称为 Pfund系列。 什么时候\(n_f = 6\),我们有汉弗莱斯系列。 你可能会猜到,氢光谱中有无限多的这样的光谱带,因为\(n_f\)可以是任何正整数。
里德伯格氢气公式给出了实验室观察到的光谱线的确切位置;但是,在二十世纪初,没有人能解释为什么它如此有效。 直到1913年提出第一个成功的氢原子模型之前,里德伯格公式一直无法解释。
计算 Balmer 系列中最长和最短的波长。
策略
我们可以使用 Balmer 公式(方程\ ref {balmer})或 Rydberg 公式(方程\ ref {rydberg})。 最长的波长是在\(1/n_i\) i 最大时获得的,也就是什么时候\(n_i = n_f + 1 = 3\),因为\(n_f = 2\)对于 Balmer 系列来说。 最小波长是在最小时获得\(1/n_i\)的,也就是说 W\(1/n_i \rightarrow 0\) hen\(n_i \rightarrow \infty\)。
解决方案
长波限制:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{3^2}\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} - \dfrac{1}{9}\right) \Rightarrow \lambda = 656.3 \, nm \nonumber \]
短波限制:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - 0\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} \right) \Rightarrow \lambda = 364.6 \, nm. \nonumber \]
意义
请注意,在这两个极限之间有无限多的光谱线。
莱曼系列的局限性是什么? 你能看见这些光谱线吗?
- 回答
-
121.5 nm 和 91.1 nm;不,这些光谱波段在紫外线中
解开原子光谱奥秘的关键在于理解原子结构。 科学家早就知道物质是由原子组成的。 根据十九世纪的科学,原子是物质中最小的不可分割量。 一系列开创性的实验证明了电子、质子和中子等亚原子粒子的存在,打破了这种科学信念。
1897 年,J.J. Thomson 在其阴极射线实验(也称为 β 射线实验)中发现并确定为最小的电荷量:β 射线是电子束。 1904年,汤姆森提出了第一个原子结构模型,称为 “梅花布丁” 模型,其中原子由未知的带正电荷的物质组成,其中嵌入了负电子,就像布丁中的李子一样。 1900 年左右,E. Rutherfor d 和独立的保罗·乌尔里希·维拉德将当时已知的所有辐射归类为射线、\(\gamma\)-射线和\(\gamma\)-射线(-射线是高能光子的光束)。\(\alpha\)\(β\) 1907年,卢瑟福和托马斯·罗伊兹使用光谱学方法证明带正电荷的\(\alpha\)辐射粒子(称为\(\alpha\)-particle)实际上是双电离的氦原子。 1909 年,卢瑟福、欧内斯特·马斯登和汉斯·盖格在他们著名的散射实验中使用了\(\alpha\)-particle,这反驳了汤姆森的模型(见线性动量和碰撞)。
在卢瑟福金箔实验(也称为盖格—马斯登实验)中,α粒子入射在薄金箔上,并被金原子散布在金箔内(参见碰撞类型)。 传出的粒子是通过围绕金靶的 360° 闪烁屏探测到的(有关实验设置的详细描述,参见线性动量和碰撞)。 当散射的粒子撞击屏幕时,在该位置观察到微小的闪光(闪烁)。 通过计算相对于入射光束方向的不同角度看到的闪烁,科学家们可以确定入射粒子中有多少是散射的,哪些部分根本没有偏转。 如果李子布丁模型是正确的,那么就不会有反向散射的 α-particle。 但是,卢瑟福实验的结果表明,尽管有相当一部分的α粒子从铝箔中冒出来,根本没有像铝箔没有挡住它们一样散落,但很大一部分α粒子是向源头反向散射的。 只有当金原子的大部分质量和全部正电荷集中在原子内部的微小空间中时,这种结果才有可能。
1911 年,卢瑟福提出了原子的核模型。 在卢瑟福的模型中,一个原子包含一个大小可以忽略不计的带正电荷的原核,几乎像一个点,但几乎包括了原子的全部质量。 原子还含有负电子,这些负电子位于原子内但离原子核相对较远。 十年后,卢瑟福为氢核创造了质子这个名字,为假设的电中性粒子创造了中子这个名字,该粒子将介导原子核中正质子的结合(中子是詹姆斯· 查德威克在1932年发现的)。 卢瑟福因发现原子核而受到赞誉;但是,卢瑟福的原子结构模型并不能解释氢气发射线的里德伯格公式。
玻尔的氢原子模型由尼尔斯·玻尔(Niels Bohr)在1913年提出,是第一个正确解释氢发射光谱的量子模型。 玻尔的模型将经典的行星运动力学与光子的量子概念相结合。 一旦卢瑟福确定了原子核的存在,玻尔关于氢原子中的负电子必须围绕正核旋转的直觉就成了静电吸引反平方距离定律的合乎逻辑的结果。 回想一下,描述两个相反电荷之间吸引力的库仑定律与牛顿的万有引力定律具有相似的形式,即引力和静电力都在减小\(1/r^2\),因为 r 是物体之间的分离距离。 就像地球围绕太阳旋转一样,氢原子中的负电子也可以围绕正原子核旋转。 但是,加速电荷会辐射其能量。 通常,如果电子以行星方式绕原子核移动,它将经历向心加速,从而辐射能量,使其螺旋向下进入原子核。 这样的行星氢原子是不稳定的,这与我们对不会分解的普通氢原子的了解相反。 此外,电子的经典运动无法解释氢气的离散发射光谱。
为了规避这两个困难,玻尔提出了玻尔模型的以下三个假设:
- 负电子在圆轨道上绕正核(质子)移动。 所有电子轨道都以原子核为中心。 并非所有传统上可能的轨道都可供与原子核结合的电子使用。
- 允许的电子轨道满足第一个量化条件:在第 n 个轨道上,电子\(L_n\)的角动量只能取离散值:\[L_n = n\hbar, \, where \, n = 1,2,3, . . . \nonumber \]这个假设表示电子的角动量是量化的。 第一个量\(r_n\)化条件分别用第 n 个轨道的半径和其中的电子速度表示,第一个量化条件可以明确表示为\(v_n\)\[m_ev_nr_n = n\hbar. \label{6.34} \]
- 允许电子从其能量所在的一个轨道过渡\(E_n\)到另一个能量所在的轨道\(E_m\)。 当原子吸收光子时,电子会过渡到能量更高的轨道。 当原子发射光子时,电子会过境到能量较低的轨道。 同时发生光子吸收或光子发射的电子转变是瞬间发生的。 允许的电子转变满足第二个量化条件:\[hf = |E_n - E_m| \nonumber \]其中\(hf\)是发射光子或吸收光子的能量和频率\(f\)。 第二个量化条件指出,氢原子中电子能量的变化是量化的。
氢原子早期量子理论的这三个假设使我们不仅能够推导出里德伯格公式,还可以推导出里德伯格常数的值以及氢原子的其他重要特性,例如其能级、电离能和电子轨道的大小。 请注意,在玻尔的模型中,除了两个非经典的量化假设外,我们还将电子描述为受库仑力影响的粒子,其运动必须遵守牛顿的运动定律。 氢原子作为一个孤立的系统,必须遵守我们从经典物理学中学到的能量守恒定律和动量守恒定律。 考虑到这个理论框架,我们准备继续进行分析。
电子轨道
为了获得电子在轨道上的大小\(r_n\)和电子在轨道\(v_n\)中的速度,我们转向牛顿力学。 作为带电粒子,电子在其圆形轨道中心经历向带正电荷的原子核的静电拉力。 这种静电拉力是一种向心力,它使电子围绕原子核围成一圈移动。 因此,向心力的大小用静电力的大小来确定:
\[ \dfrac{m_ev_n^2}{r_n} = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n^2}. \label{6.36} \]
这里\(e\)表示基本电荷的值。 负电子和正质子的电荷值相同,
\[|q| = e. \nonumber \]
当方程\ ref {6.36} 与方程\ ref {6.34} 给出的第一个量化条件组合时\(v_n\),我们可以求解速度和半径\(r_n\):
\[v_n = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{\hbar} \dfrac{1}{n} \label{6.37} \]
\[r_n = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2}n^2. \label{6.38} \]
请注意,这些结果告诉我们,电子的速度及其轨道半径仅取决于枚举轨道的索引 n,因为前面方程中的所有其他量都是基本常数。 我们从方程式\ ref {6.38} 中看出,轨道的大小随着 n 的平方而增长。 这意味着第二个轨道是第一个轨道的四倍,第三个轨道是第一个轨道的九倍,依此类推。 我们还从方程式\ ref {6.37} 中看出,随着轨道大小的增加,电子在轨道上的速度会降低。 在第一个玻尔轨道上,电子的速度最大\(n = 1\),因为这是最接近原子核的轨道。 第一个玻尔轨道的半径称为玻尔氢气半径,表示为\(a_0\)。 它的值是通过\(n = 1\)在方程式\ ref {6.38} 中设置来获得的:
\[a_0 = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2} = 5.29 \times 10^{-11} m = 0.529\space Å. \nonumber \]
我们可以在方程式\ ref {6.38}\(a_0\) 中替换为用以下方式表示第 n 个轨道的半径\(a_0\):
\[r_n = a_0n^2. \label{6.40} \]
这个结果意味着氢原子中的电子轨道是量化的,因为轨道半径仅采用方程\ ref {6.40} 给出的、、\(16a_0\)... 的特定值,不允许使用其他值。\(a_0\)\(4a_0\)\(9a_0\)
电子能量
电子在第 n\(E_n\) 个轨道上的总能量是其动能\(K_n\)和静电势能之和\(U_n\)。 利用方程式\ ref {6.37},我们发现
\[K_n = \dfrac{1}{2}m_ev_n^2 = \dfrac{1}{32\pi^2 \epsilon^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.41} \]
回想一下,两个电荷之间相互作用\(q_1\)且\(q_2\)相隔一定距离的静电势能\(r_{12}\)为\((1/4\pi \epsilon_0)q_1q_2/r_{12}\)。 这里\(q_1 = +e\)是氢原子中原子核的电荷(质子的电荷),\(q_2 = -e\)是电子的电荷,\(r_{12} = r_n\)是第 n 个轨道的半径。 现在我们使用方程\ ref {6.38} 来找出电子的势能:
\[U_n = - \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n} = - \dfrac{1}{16\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.42} \]
电子的总能量是方程\ ref {6.41} 和方程\ ref {6.42} 的总和:
\[E_n = K_n + U_n = - \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.43} \]
请注意,能量仅取决于指数 n,因为方程\ ref {6.43} 中的其余符号是物理常数。 方程\ ref {6.43} 中常数因子的值为
\[E_0 = \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} = \dfrac{1}{8\epsilon_0^2} \dfrac{m_ee^4}{h^2} = 2.17 \times 10^{-18} J = 13.6 \, eV. \label{6.44} \]
用这种能量来表示电子在第 n 个轨道上的能量很方便,因为
\[E_n = -E_0 \dfrac{1}{n^2}. \label{6.45} \]
现在我们可以看到,氢原子中的电子能量是量化的,因为它们只能有方程\ ref {6.45}\(-E_0, \, -E_0/4, \, -E_0/9, \, -E_0/16, . . . \) 给出的离散值,不允许使用其他能量值。 这组允许的电子能量被称为氢的能量谱(图\(\PageIndex{5}\))。 枚举玻尔模型中能级的指数 n 称为能量量子数。 我们将氢原子内部电子的能量与氢原子的能量相提并论。 请注意,获得的最小能量值为\(n = 1\),因此氢原子的能量不能小于该值。 氢原子中电子能量的最小值称为氢原子的基态能,其值为
\[E_1 = −E_0 = −13.6 \, eV. \label{6.46} \]
氢原子可能具有高于基态的其他能量。 这些更高的能量态被称为氢原子的激发能量态。
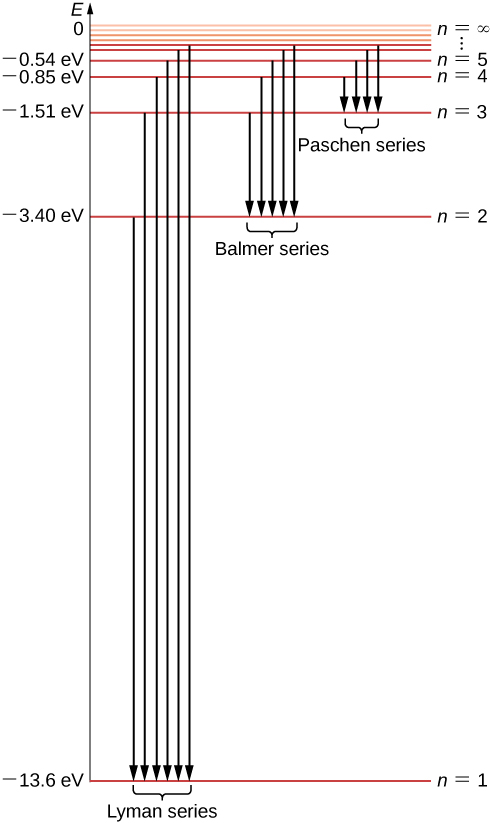
只有一个基态,但是有无限多的激发态,因为方程\ ref {6.45} 中有 n 的值无限多。 我们说,当电子的能量为\(E_n\)(何时\(n = 2\))时,电子处于 “第一退出状态”,当其能量为\(E_3\)(何时\(n = 3\))时处于第二激发态,一般而言,当其能量为时,处于第 n 个退出状态\(E_n + 1\)。 没有最高的激发态;但是,激发态的序列是有限的。 如果我们在方程式\ ref {6.45}\(n\) 中继续增加,就会发现极限是\(- lim_{n \rightarrow \infty} \, E_0/n^2 = 0\)。 在这个极限下,电子不再与原子核结合,而是变成了自由电子。 只要能量为负,电子就会与氢原子结合。 在第一个玻尔轨道上绕原子核运行、最靠近原子核的电子处于基态,其能量值最小。 在基态下,电子与原子核的结合力最强,其能量由方程\ ref {6.46} 给出。 如果我们想从原子中移除这个电子,就必须为它提供足够的能量\(E_{\infty}\),至少平衡其基态能量\(E_1\):
\[E_{\infty} + E_1 = 0 \Rightarrow E_{\infty} = - E_1 = - (- E_0) = E_0 = 13.6 \, eV. \label{6.47} \]
将电子从原子中移除所需的能量称为电离能。 将电子从第一个玻尔轨道移出所需的电离能\(E_{\infty}\)称为氢原子的电离极限。 我们在玻尔模型中获得的方程\ ref {6.47} 中的电离极限与实验值一致。
氢气的光谱发射线
为了获得电子从第 n 个轨道过渡到第 m 个轨道时发射辐射的波长,我们使用玻尔的第二个量化条件和方程\ ref {6.45} 表示能量。 只有当电子从激发态过渡到低能态时,才能从原子发射能量。 在这样的过渡过程中,发射的光子带走了过渡所涉及的状态之间的能量差。 过渡不能朝另一个方向发展,因为光子的能量不能为负,这意味着我们必须有\(E_n > E_m\)和\(n > m\)。 因此,玻尔的第三个假设给出了
\[\begin{align} hf &= |E_n - E_m| \nonumber \\[4pt] &= E_n - E_m \nonumber \\[4pt] &= -E_0 \dfrac{1}{n^2} + E_m \dfrac{1}{m^2} \nonumber \\[4pt] &= E_0 \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.48} \end{align} \]
现在我们用光子的波长表示光子的能量\(hf = hc/\lambda\),然后将方程\ ref {6.48} 的两边除以\(hc\)。 结果是
\[ \dfrac{1}{\lambda} = \dfrac{E_0}{hc} \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.49} \]
此方程中常量的值为
\[\dfrac{E_0}{hc} = \dfrac{13.6 \, eV}{(4.136 \times 10^{-15} eV \cdot s)(2.997 \times 10^8 m/s)} = 1.097 \times 10^7 \dfrac{1}{m}. \label{6.50} \]
这个值正是 Rydberg 启发式公式方程\ ref {rydberg}\(R_H\) 中的里德伯格常数。 实际上,方程\ ref {6.49} 与 Rydberg 公式相同,因为对于给定的 m,我们有\(n = m + 1, \, m + 2, . . .\)。 通过这种方式,氢原子的玻尔量子模型使我们能够从第一原理推导出实验性的里德伯格常数,并用基本常数来表达。 允许的电子轨道之间的过渡如图所示\(\PageIndex{5}\)。
我们可以重复生成方程\ ref {6.49} 的相同步骤来获得吸收辐射的波长;这再次给出了方程\ ref {6.49},但这次是针对氢气吸收光谱中吸收线的位置。 唯一的区别是,对于吸收而言,量子数\(m\)是电子在过渡之前占据的轨道指数(低能轨道),量子数\(n\)是电子过渡到的轨道(高能轨道)的指数。 这两个轨道中电子能量的区别在于吸收的光子的能量。
如果处于基态的氢原子吸收了93.7纳米的光子,对应于莱曼系列中的过渡线,这将如何影响原子的能量和大小? 当原子处于这种激发态时,电离需要多少能量? 以绝对单位和相对于基态给出答案。
策略
在吸收之前,原子处于基态。 这意味着电子从轨道过渡\(m = 1\)到轨道上更高的轨道。 首先,我们必须确定吸收波长的 nn\(\lambda = 93.7 \, nm\)。 然后,我们可以使用方程\ ref {6.45} 来找到激发态\(E_n\)的能量及其电离能\(E_{\infty,n}\),然后使用方程\ ref {6.40} 来找出处于激发态的原\(r_n\)子的半径。 为了估计 n,我们使用方程\ ref {6.49}。
解决方案
在方程式\ ref {6.49} 中替换\(m = 1\) lb = 93.7 nm 然后求解 n。你不应该因为四舍五入误差而期望得到一个完美的整数答案,但你的答案将接近一个整数,你可以通过取答案的积分部分来估计 n:
\[ \begin{align*} \dfrac{1}{\lambda} &= R_H \left( \dfrac{1}{1^1} - \dfrac{1}{n^2}\right) \\[4pt] \Rightarrow n &= \dfrac{1}{\sqrt{1 - \dfrac{1}{\lambda R_H}}} \\[4pt] &= \dfrac{1}{\sqrt{1 - \dfrac{1}{(93.7 \times 10^{−9}m)(1.097 \times 10^7 m^{−1})}}} \\[4pt] &= 6.07 \\[4pt] \Rightarrow n &= 6. \end{align*} \]
\(n = 6\)轨道的半径是
\[r_n = a_0n^2= a_06^2 = 36a_0 = 36(0.529 \times 10^{−10} \, m) = 19.04 \times 10^{−10}\space m ≅ 19.0 \, Å. \nonumber \]
因此,在吸收了93.7纳米光子之后,\(n = 6\)处于激发态的氢原子的大小比吸收之前(当时原子处于基态)大36倍。 第五个激发态 (\(n = 6\)) 的能量是:
\[E_n = - \dfrac{E_0}{n^2} = - \dfrac{E_0}{6^2} = - \dfrac{E_0}{36} = - \dfrac{13.6 \, eV}{36} ≅ − 0.378 \, eV. \nonumber \]
吸收 93.7 纳米光子后,氢原子的能量大于吸收前的能量。 原子处于第五激发态时的电离所需的能量比原子处于基态时所需的能量少36倍:\(n = 6\)
\[E_{\infty,6} = -E_6 = -(-0.378 \, eV) = 0.378 \, eV. \nonumber \]
意义
我们可以用同样的方式分析氢气光谱中的任何光谱线。 因此,光谱线的实验测量为我们提供了有关氢原子原子结构的信息。
当氢原子中的电子处于第一激发态时,玻尔模型对其轨道速度和动能做出了什么预测? 它的轨道角动量的大小是多少?
- 回答
-
\(v_2 = 1.1 \times 10^6 m/s ≅0.0036 \, c;\)
\(L_2 = 2\hbar K_2 = 3.4 \, eV\)
玻尔的氢原子模型还正确地预测了一些类氢离子的光谱。 类氢离子是原子序数 Z 大于 1 的元素的原子(\(Z = 1\)对于氢气),但除了一个电子外,所有电子都被移除。 例如,电中性的氦原子具有原子序数\(Z = 2\)。 这意味着它有两个电子绕原子核运行,电荷为\(q = +Ze\)。 当其中一个轨道电子从氦原子中移除时(我们说,当氦原子被单独电离时),剩下的是一个类似氢的原子结构,剩下的电子以电荷绕原子核运行\(q = +Ze\)。 玻尔模型描述了这种情况。 假设原子核的电荷不是\(+e\)但是\(+Ze\),我们可以重复所有步骤,从方程\ ref {6.36} 开始,以获得类氢离子的结果:
\[r_n = \dfrac{a_0}{Z}n^2 \label{6.51} \]
氢气\(a_0\)的玻尔轨道在哪里,
\[E_n = -Z^2E_0 \dfrac{1}{n^2} \label{6.52} \]
氢原子的电离极限在哪里\(E_0\)。 只要原子序数 Z 不太大,这些方程就是很好的近似值。
玻尔模型很重要,因为它是第一个假设原子中电子轨道量化的模型。 因此,它代表了早期的量子理论,它为现代量子理论的发展提供了开端。 它引入了量子数的概念来描述原子态。 早期量子理论的局限性在于它无法描述绕原子核运行的电子数量大于一个的原子。 玻尔氢气模型是一种半经典模型,因为它结合了电子轨道的经典概念和新的量化概念。 该模型的巨大成功促使许多物理学家寻求解释为什么这样的模型应该起作用,并寻求对早期量子理论假设背后的物理学的理解。 这次搜索催生了一个全新的 “物质波” 概念。


