6.4: 康普顿效应
- Page ID
- 202019
在本节结束时,您将能够:
- 描述康普顿的实验
- 解释康普顿波长偏移
- 描述 X 射线实验如何确认辐射的粒子性质
爱因斯坦在1905年提出的两个有影响力的思想是狭义相对论和光量子概念,我们现在称之为光子。 1905年以后,爱因斯坦进一步提出,自由传播的电磁波由光子组成,光子是光的粒子,就像电子或其他大粒子是物质粒子一样。 波长\(\lambda\)(或等效频率\(f\))的单色光束既可以看作是经典的波,也可以看作是光子的集合,这些光子在真空中以一种速度\(c\)(光速)传播,并且都携带相同的能量\(E_f = hf\)。 事实证明,这个想法对于解释光与物质粒子的相互作用很有用。
光子的动量
与以静止质量为特征的物质粒子不同\(m_0\),光子是无质量的。 在真空中,与可能改变速度但无法达到光速的物质粒子不同,光子只能以一种速度移动,也就是光速。 从牛顿经典力学的角度来看,这两个特征意味着光子根本不应该存在。 例如,我们怎样才能找到质量为零的物体的线性动量或动能? 如果我们将光子描述为相对论粒子,这种明显的悖论就会消失。 根据狭义相对论,自然界中的任何粒子都服从相对论能量方程
\[E^2 = p^2c^2 + m_0^2c^4. \label{6.17} \]
这种关系也可以应用于光子。 在方程\ ref {6.17} 中,\(E\)是粒子的总能量,\(p\)是其线性动量,\(m_0\)是其静止质量。 对于光子,我们只需\(m_0 = 0\)在方程式\ ref {6.17} 中进行设置,即可得出光子动\(p_f\)量的表达式
\[p_f = \dfrac{E_f}{c}. \label{6.18} \]
这里光子的能量与光\(E_f\)量子频率的能量相同\(f\),我们用它来解释光电效应:
\[E_f = hf = \dfrac{hc}{\lambda}. \label{6.19} \]
将频率\(f\)与波长\(λ\)和速度联系起来的波浪关系\(c\)也适用于光子:
\[\lambda f = c \label{6.20} \]
因此,光子可以通过其能量和波长或频率和动量来等效地表征。 方程\ ref {6.19} 和\ ref {6.20} 可以组合成光子动量与其波长之间的显式关系:
\[p_f = \dfrac{h}{\lambda}. \label{6.21} \]
请注意,这个方程只给出了光子动量的大小,不包含有关光子移动方向的信息。 要包括方向,习惯上将光子的动量写成矢量:
\[\vec{p}_f = \hbar \vec{l}. \label{6.22} \]
在方程\ ref {6.22} 中,\(\hbar = h/2\pi\)是简化的普朗克常数(发音为 “h-bar”),它只是普朗克常数除以因子\(2\pi\)。 向\(\vec{l}\)量被称为 “波向量” 或传播矢量(光子的移动方向)。 传播向量显示光子的线性动量向量的方向。 波向量的大小为
\[k = |\vec{k}| = 2\pi /\lambda \nonumber \]
并被称为波数。 请注意,这个方程并未引入任何新的物理学。 我们可以验证方程\ ref {6.22} 中向量的大小与方程\ ref {6.18} 给出的值相同。
康普顿效应
康普顿效应是指当X射线散射在某些材料上时观察到的异常结果的术语。 根据经典理论,当电磁波从原子上散射时,散射辐射的波长应与入射辐射的波长相同。 与经典物理学的这种预测相反,观察结果表明,当X射线从某些材料(例如石墨)上散射时,散射的X射线的波长与入射的X射线的波长不同。 亚瑟·康普顿及其合作者通过实验研究了这种经典的无法解释的现象,康普顿在1923年给出了解释。
为了解释实验中测得的波长的变化,康普顿使用了爱因斯坦将光视为粒子的概念。 康普顿效应在物理学史上占有非常重要的地位,因为它表明电磁辐射不能解释为纯粹的波浪现象。 对康普顿效应的解释为物理学界提供了一个令人信服的论点,即电磁波的行为确实可以像光子流一样,这使光子的概念有了坚实的基础。
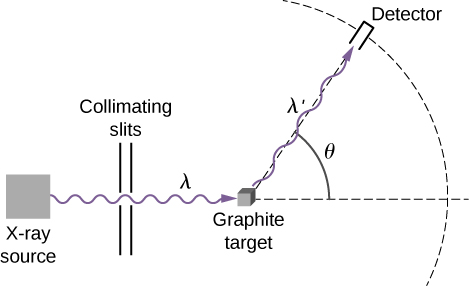
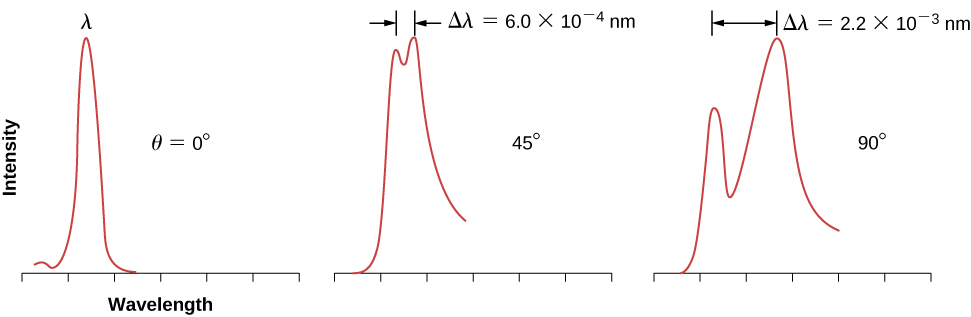
康普顿实验装置的示意图如图所示\(\PageIndex{1}\)。 实验的想法很简单:具有波长的\(λ\)单色X射线入射到石墨样品(“目标”)上,它们与样品内部的原子相互作用;它们随后以具有波长的散射X射线形式出现\(λ'\)。 放置在目标后面的探测器可以测量\(θ\)相对于入射的 X 射线束方向向任何方向散射的辐射强度。 这个散射角是散射光束的方向和入射光束的方向之间的角度。\(θ\) 在这个实验中,我们知道入射(入射)光束\(λ\)的强度和波长;对于给定的散射角度\(θ\),我们测量传出(散射)光束\(λ'\)的强度和波长。 这些测量的典型结果如图所示\(\PageIndex{2}\),其中\(x\)-axis 是散射 X 射线的波长,\(y\)-axis 是散射 X 射线的强度,在不同的散射角度(如图所示)下测量。 对于所有散射角度(除外\(θ=0°\)),我们测量两个强度峰值。 一个峰位于波长\(λ\),即入射光束的波长。 另一个峰位于其他波长,\(λ'\)。 两个峰之间用分隔\(Δλ\),这取决于出射光束\(θ\)的散射角度(在观测方向)。 这种分离\(Δλ\)被称为康普顿轮班。
康普顿转移
正如康普顿给出的那样,对康普顿偏移的解释是,在目标材料石墨中,价电子松散地结合在原子中,表现得像自由电子。 康普顿假设入射的X射线辐射是光子流。 该流中的入射光子与石墨目标中的价电子碰撞。 在这次碰撞过程中,传入的光子将其部分能量和动量传递给目标电子,并作为散射光子离开场景。 该模型从定性角度解释了为什么散射辐射的波长比入射辐射长。 简而言之,失去部分能量的光子以频率较低或等效波长较长的光子出现。 为了证明他的模型是正确的,康普顿用它来推导康普顿偏移的表达式。 在他的推导中,他假设光子和电子都是相对论粒子,碰撞遵循两个常识性原则:
- 线性动量的守恒和
- 总相对论能量的守恒。
在接下来的康普顿偏移推导中,\(E_f\)和分别\(\vec{p}_f\)表示频率入射光子的能量和动量\(f\)。 光子在静止时与相对论电子碰撞,这意味着在碰撞之前,电子的能量完全是其静止质量能\(m_0c^2\)。 碰撞后,电子立即获得能量\(E\)和动量\(\vec{p}\),两者都满足方程\ ref {6.19}。 碰撞后,传出的光子立即具有能量\(\vec{\tilde{E}}_f\)\(\vec{\tilde{p}}_f\)、动量和频率\(f'\)。 入射光子的方向从左到右是水平的,而传出光子的方向是这个角度\(θ\),如图所示\(\PageIndex{1}\)。 散射角\(θ\)是动量向量\(\vec{p}_f\)和之间的角度\(\vec{\tilde{p}}_f\),我们可以写出它们的标量积:
\[\vec{p} \cdot \vec{\tilde{p}}_f = p_f\vec{p}_f \cos \, \theta. \label{6.23} \]
根据康普顿的论点,我们假设碰撞的光子和电子形成了一个孤立的系统。 这种假设适用于弱绑定电子,可以很好地将弱绑定电子视为自由粒子。 我们的第一个方程是光子电子系统的能量守恒:
\[E_f + m_0c^2 = \tilde{E}_f + E. \label{6.24} \]
该方程的左侧是系统在碰撞前一刻的能量,而方程的右侧是系统在碰撞后不久的能量。 我们的第二个方程是光子-电子系统的线性动量守恒,在该系统中,电子在碰撞前一刻处于静止状态:
\[\vec{p}_f = \vec{\tilde{p}}_f + \vec{p}. \label{6.25} \]
该方程的左侧是碰撞前系统的动量,方程的右侧是碰撞后系统的动量。 康普顿散射的整个物理学都包含在前面的三个方程中,其余部分是代数。 此时,我们可以跳转到康普顿移位的总结公式,但重点介绍导致康普顿公式的主要代数步骤是有益的,我们在此给出了如下所示。
我们首先重新排列方程\ ref {6.24} 中的项,然后将其平方:
\[[(E_f - \tilde{E}_f) + m_0c^2]^2 = E^2. \nonumber \]
在下一步中,我们用方程\ ref {6.19} 代替\(E^2\)、简化并除以两边得\(c^2\)到
\[(E_f / c - \tilde{E}_f / c)^2 + 2m_0c (E_f / c - \tilde{E}_f / c) = p^2. \nonumber \]
现在我们可以使用方程\ ref {6.21} 用力矩来表示这种形式的能量方程。 结果是
\[(p_f - \tilde{p}_f)^2 + 2m_0 c(p_f - \tilde{p}_f) = p^2. \label{6.26} \]
为了消除\(p^2\),我们转向动量方程式\ ref {6.25},重新排列其项,然后将其平方得到
\[ \begin{align*} (\vec{p}_f - \vec{\tilde{p}}_f)^2 &= p^2 \\[4pt] &= p_f^2 + \tilde{p}_f^2 - 2p_f \tilde{p}_f \, \cos \, \theta. \end{align*} \nonumber \]
动量向量的乘积由方程\ ref {6.23} 给出。 当我们在方程式\ ref {6.26}\(p^2\) 中用这个结果代替时,我们得到包含散射角 β 的能量方程:
\[(p_f - \tilde{p}_f)^2 + 2m_0c(p_f - \tilde{p}_f) = p_f^2 + \tilde{p}_f^2 - 2p_f \tilde{p}_f \, \cos \, \theta. \nonumber \]
通过进一步的代数,这个结果可以简化为
\[\dfrac{1}{\tilde{p}_f} - \dfrac{1}{p_f} = \dfrac{1}{m_0c}(1 - \cos \, \theta). \label{6.27} \]
现在回忆方程\ ref {6.21} 然后写上:\(1/\tilde{p}_f = \lambda' /h\)和\(1/p_f = \lambda /h\)。 当将这些关系替换为方程\ ref {6.27} 时,我们得到康普顿偏移的关系:
\[\lambda' - \lambda = \dfrac{h}{m_0c}(1 - \cos \, \theta). \label{6.28} \]
该因子\(h/m_0c\)称为电子的康普顿波长:
\[\lambda_c = \dfrac{h}{m_0c} = 0.00243 \, nm = 2.43 \, pm. \label{6.29} \]
将转变表示为\(\Delta \lambda = \lambda' - \lambda\),结论结果可以改写为
\[\Delta \lambda = \lambda_c (1 - \cos \, \theta). \label{6.30} \]
康普顿移位的这个公式很好地描述了图中所示的实验结果\(\PageIndex{2}\)。 测得的钼、石墨、方解石和许多其他目标材料的散射数据与该理论结果一致。 图中所示的非移位峰\(\PageIndex{1}\)是由于光子与目标材料中紧密结合的内部电子发生碰撞所致。 与目标原子的内部电子碰撞的光子实际上与整个原子碰撞。 在这种极端情况下,方程\ ref {6.29} 中的剩余质量必须更改为原子的剩余质量。 这种类型的偏移比与电子碰撞引起的偏移小四个数量级,而且很小,不容忽视。
康普顿散射是非弹性散射的一个例子,其中散射辐射的波长比入射辐射的波长长。 在当今的用法中,“康普顿散射” 一词用于自由带电粒子对光子进行非弹性散射。 在康普顿散射中,将光子视为具有可以转移到带电粒子的力量的粒子,这为解释实验中测得的波长变化提供了理论背景;这证明辐射由光子组成。
晚上 7 点 1 点发生的 X 射线事件发生在方解石目标上。 找出以 30°30° 角散射的 X 射线的波长。 在这个实验中,可以预期的最大变化是什么?
策略
要找到散射 X 射线的波长,首先我们必须找到给定散射角度的康普顿偏移\(\theta = 30°\)。 我们使用方程式\ ref {6.30}。 然后我们将这种偏移加到入射波长中以获得散射波长。 最大的康普顿偏移发生在\(1 - \cos \, \theta\)具有最大值\(\theta\)时的角度,即角度\(\theta = 180°\)。
解决方案
现在的转变\(\theta = 30°\)是
\[\begin{align*} \Delta \lambda &= \lambda_c (1 - \cos \, 30°) \\[4pt] &= 0.134 \lambda_c \\[4pt] &= (0.134)(2.43) \, pm \\[4pt] &= 0.32 \end{align*} \nonumber \]
这给出了散射波长:
\[\begin{align*} \lambda' &= \lambda + \Delta \lambda \\[4pt] &= (71 + 0.325) \, pm \\[4pt] &= 71.325 \,pm. \end{align*} \nonumber \]
最大的转变是
\[\begin{align*} (\Delta \lambda )_{max} &= \lambda_c(1 − \cos \, 180°) \\[4pt] &= 2(2.43 \, pm) \\[4pt] &= 4.86 \, pm. \end{align*} \nonumber \]
意义
检测到的波长变化最大的是反向散射辐射;但是,来自入射光束的大多数光子都会穿过目标,只有一小部分光子会反向散射(通常小于5%)。 因此,这些测量需要高度灵敏的探测器。
晚上 7 点 1 点发生的 X 射线事件发生在方解石目标上。 找出以 60° 角散射的 X 射线的波长。 在这个实验中可以预期的最小变化是多少?
- 回答
-
\((\Delta \lambda)_{min} = 0 \, m\)成0°角;\(71.0 \, pm + 0.5 \lambda_c = 72.215 \, pm\)


