6.3: 光电效应
- Page ID
- 202027
在本节结束时,您将能够:
- 描述光电效应的物理特征
- 解释为什么经典物理学无法解释光电效应
- 描述爱因斯坦对辐射粒子的看法如何解释光电效应
当金属表面暴露于波长足够短(或等效地,高于阈值频率)的单色电磁波时,入射辐射被吸收,暴露的表面会发射电子。 这种现象被称为光电效应。 在此过程中发射的电子称为光电子。
图中示意性地显示了研究光电效应的实验装置\(\PageIndex{1}\)。 目标材料充当阳极,当它被单色辐射照亮时,阳极成为光电子的发射器。 我们称这个电极为光电极。 光电子收集在阴极处,阴极相对于阳极保持较低的电位。 电极之间的电位差可以增加或减少,也可以反转其极性。 电极封闭在真空玻璃管中,这样光电子在与电极之间空间中的空气分子碰撞时不会失去动能。
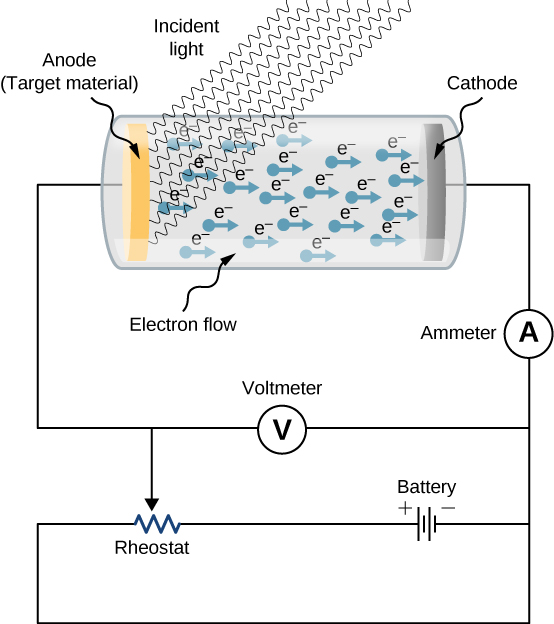
当目标材料没有受到辐射时,由于电路已损坏,因此该电路中不会记录电流(注意,电极之间存在间隙)。 但是,当目标材料连接到电池的负极并暴露于辐射下时,电流就会记录在该电路中;这种电流称为光电流。 假设我们现在反转了电极之间的电位差,这样目标材料现在可以连接到电池的正极,然后我们慢慢增加电压。 在这个反向电压的某个值下,光电流逐渐消失,最终完全停止流动。 光电流停止流动的电位差称为停止电位。
光电效应的特征
光电效应具有经典物理学无法解释的三个重要特征:(1)没有延迟时间;(2)光电子的动能与入射辐射强度的独立性;(3)存在截止频率。 让我们研究一下其中的每一个特征。
没有延迟时间
当辐射撞击电极中的目标材料时,即使入射辐射强度非常低,电子也几乎是瞬间发射的。 这种没有延迟时间的情况与我们基于经典物理学的理解相矛盾。 经典物理学预测,对于低能辐射,经过辐照的电子需要很长时间才能获得足够的能量离开电极表面;但是,没有观察到这种能量积聚。
入射辐射的强度和光电子的动能
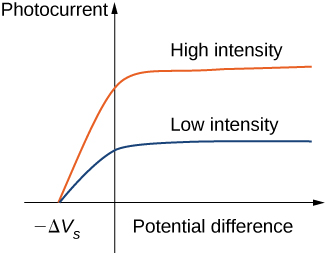
典型的实验曲线如图所示\(\PageIndex{2}\),其中绘制了光电流与电极之间施加的电位差。 对于正电位差,电流会稳步增长,直到达到稳定状态。 在此之后进一步增加电位根本不会增加光电流。 辐射强度越高,产生的光电流值越高。 对于负电位差,随着电位差绝对值的增加,光电流的值减小并在停止电位处变为零。 对于任何强度的入射辐射,无论强度是高还是低,停止电位的值始终保持在一个值。
要理解为什么从经典物理学的角度来看这个结果不寻常,我们首先必须分析光电子的能量。 离开表面的光电子具有动能\(K\)。 它从入射的电磁波中获得了这种能量。 在电极之间的空间中,光电子在电势中移动,其能量随之变化\(q \Delta V\),其中\(\Delta V\)是电位差和\(q = -e\)。 因为除了电力之外没有力存在,所以通过应用工作能量定理,我们可以获得光电子的能量平衡\(\Delta K - e\Delta V = 0\),其中\(\Delta K\)是光电子动能的变化。 施加停止电\(-\Delta V_s\)位时,光电子会失去其初始动能\(K_i\)并开始休息。 因此,它的能量平衡\((0 - K_i) - e(-\Delta V_s) = 0\)就变成了\(K_i = e\Delta V_s\)。 在存在停止电位的情况下,光电子可以拥有的最大动能\(K_{max}\)是其在光电极表面的初始动能。 因此,可以通过测量停止电位来直接测量光电子的最大动能:
\[K_{max} = e\Delta V_s. \label{PEexpt} \]
此时我们可以看到经典理论与实验结果的矛盾之处。 在经典理论中,光电子以连续的方式吸收电磁能量;这意味着当入射辐射的强度很高时,方程\ ref {peexpt} 中的动能预计会很高。 同样,当辐射强度较低时,动能预计会很低。 但是实验表明,光电子的最大动能与光强无关。
存在截止频率
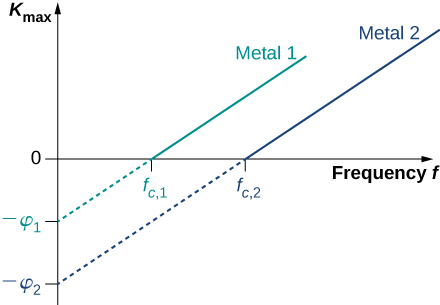
对于任何金属表面,都有最低入射辐射频率,低于该频率不会产生光电流。 光电效应的这种截止频率的值是金属的物理特性:不同的材料具有不同的截止频率值。 实验数据显示了典型的线性趋势(图\(\PageIndex{3}\))。 随着入射辐射频率的增加,表面光电子的动能呈线性增长。 所有金属表面的测量结果得出一个斜率的线性图。 这些观察到的现象都不符合对自然的传统理解。 根据经典的描述,光电子的动能根本不应取决于入射辐射的频率,也不应有截止频率。 相反,在经典画面中,电子以连续的方式从入射电磁波中接收能量,而它们接收的能量仅取决于入射光的强度,不取决于其他任何东西。 因此,按照传统的理解,只要光线照耀,光电效应有望持续下去。
工作职能
爱因斯坦在 1905 年解释了光电效应。 爱因斯坦认为,如果普朗克关于能量量子的假设在描述电磁辐射和空腔壁之间的能量交换方面是正确的,那么它也应该有助于描述光电极表面对电磁辐射的能量吸收。 他假设电磁波以离散包的形式传送能量。 爱因斯坦的假设超出了普朗克的假设,因为它指出光本身由能量量子组成。 换句话说,它指出电磁波是量化的。
在爱因斯坦的方法中,频率的单色光束\(f\)是由光子组成的。 光子是光的粒子。 每个光子都以光速移动并携带能量子\(E_f\)。 光子的能量仅取决于其频率\(f\)。 显而易见,光子的能量是
\[E_f = hf \label{planck} \]
普朗克的常数在哪里\(h\)。 在光电效应中,光子到达金属表面,每个光子将其所有能量释放给金属表面上的一个电子。 这种从光子到电子的能量转移属于 “要么全有要么全无” 的类型,在分数转移中,光子只会损失部分能量而存活。 量子现象的本质是要么是光子转移其全部能量然后不存在,要么根本没有转移。 这与允许分数能量转移的经典画面形成鲜明对比。 有了这种量子理解,表面上\(E_f\)从光子接收能量的电子的能量平衡是
\[E_f = K_{max} + \phi \nonumber \]
哪里\(K_max\)是由方程\ ref {peexpt} 给出的电子在脱离表面时所拥有的动能。 在这个能量平衡方程中,\(\phi\)是将光电子从表面分离所需的能量。 这种能\(\phi\)量被称为金属的功函数。 每种金属都有其特有的工作功能,如表所示\(\PageIndex{1}\)。 为了获得表面光电子的动能,我们只需反转能量平衡方程并使用方程\ ref {planck} 来表示吸收光子的能量。 这为我们提供了光电子动能的表达式,这明确取决于入射辐射的频率:
\[K_{max}=hf−ϕ \label{PEeffect} \]
方程\ ref {peEffect} 的数学形式很简单,但其物理学却很深刻。 我们现在可以详细说明这个方程式背后的物理意义。
| 金属 | \(\phi\)(eV) |
|---|---|
| 娜 | \ (\ phi\) (eV)” >2.46 |
| 阿尔 | \ (\ phi\) (eV)” >4.08 |
| Pb | \ (\ phi\) (eV)” >4.14 |
| 锌 | \ (\ phi\) (eV)” >4.31 |
| 铁 | \ (\ phi\) (eV)” >4.50 |
| 铜 | \ (\ phi\) (eV)” >4.70 |
| Ag | \ (\ phi\) (eV)” >4.73 |
| Pt | \ (\ phi\) (eV)” >6.35 |
在爱因斯坦的解释中,相互作用发生在单个电子和单个光子之间。 没有延迟时间意味着这些一对一的互动是即时发生的。 降低光强度无法增加这种交互时间。 光强对应于单位时间内到达金属表面的光子数量。 即使在非常低的光强度下,光电效应仍然会发生,因为这种相互作用发生在一个电子和一个光子之间。 只要至少有一个光子具有足够的能量将其转移到绑定电子上,光电极表面就会出现光电子。
光电效应截止频率\(f_c\)的存在来自方程\ ref {peEffect},因为光电子\(K_{max}\)的动能只能取正值。 这意味着必须存在动能为零的某个阈值频率\(0 = hf_c - \phi\)。 通过这种方式,我们可以获得截止频率的显式公式:
\[f_c = \frac{\phi}{h}. \label{6.15} \]
截止频率仅取决于金属的工作功能,并且与之成正比。 当功函数较大时(当电子快速绑定到金属表面时),阈值光子的能量必须很大才能产生光电子,然后相应的阈值频率就会很大。 频率大于阈值频率的光子\(f_c\)总是会产生光电子,因为它们有\(K_{max} > 0\)。 频率小于以下频率的光子\(f_c\)没有足够的能量来产生光电子。 因此,当入射辐射的频率低于截止频率时,不会观察到光电效应。 由于电磁波\(\lambda\)的频率\(f\)和波长由基本关系\(\lambda f = c\)(其中 cc 是真空中的光速)相关,因此截止频率具有相应的截止波长\(\lambda_c\):
\[\lambda_c = \frac{c}{f_c} = \frac{c}{\phi /h} = \frac{hc}{\phi}. \label{6.16} \]
在这个方程式中,\(hc = 1240 \, eV \cdot nm\). 可以用以下等效方式重述我们的观测结果:当入射辐射的波长长超过截止波长时,光电效应不会发生。
波长 300 nm 的辐射入射在银表面上。 会观察到光电子吗?
策略
只有当入射辐射的波长短于截止波长时,光电子才能从金属表面喷出。 白银的工作功能是\(\phi = 4.73 \, eV\)(表\(\PageIndex{1}\))。 为了进行估算,我们使用方程\ ref {6.16}。
解决方案
观察银中光电效应的阈值波长为
\[\begin{align*} \lambda_c &= \frac{hc}{\phi} \\[4pt] &= \frac{1240 \, eV \cdot nm}{4.73 \, eV} = 262 \, nm. \end{align*} \nonumber \]
入射辐射的波长为 300 nm,比截止波长长;因此,未观察到光电子。
意义
如果光电极由钠而不是银制成,则截止波长将为 504 nm,并且可以观察到光电子。
爱因斯坦模型中的方程\ ref {peEffect} 告诉我们,光电子的最大动能是入射辐射频率的线性函数,如图所示\(\PageIndex{3}\)。 对于任何金属,此图的斜率值均为普朗克常数。 \(K_{max}\)-axis 的截距为我们提供了金属所特有的功函数值。 另一方面,\(K_{max}\)可以在实验中通过测量光电流停止的停止电位的值\(\delta V_s\)(参见方程\ ref {peexpt})来直接测量。 这些直接测量使我们能够通过实验确定普朗克常数的值以及材料的工作函数。
爱因斯坦的模型还直接解释了图中所示的光电流值\(\PageIndex{3}\)。 例如,将辐射强度加倍意味着单位时间内撞击表面的光子数量增加一倍。 光子数量越多,光电子的数量就越大,这会导致电路中的光电流越大。 这就是辐射强度影响光电流的方式。 光电流必须达到一定电位差值的平稳,因为在单位时间内,光电子的数量等于入射光子的数量,入射光子的数量根本不取决于施加的电位差,而只取决于入射辐射的强度。 停止电位不会随辐射强度而变化,因为光电子的动能(参见方程\ ref {peEffect})不依赖于辐射强度。
当在对未知金属进行实验时使用 180 纳米光时,测得的光电流在电位处降至零 — 0.80 V。确定金属的工作函数及其光电效应的截止频率。
策略
要找到截止频率\(f_c\),我们使用方程\ ref {6.15},但首先我们必须找到工作函数\(\phi\)。 为了找到\(\phi\),我们使用方程\ ref {peexpt} 和方程\ ref {peEffect}。 在电位停止值时,光电流降至零,因此我们可以识别\(\Delta V_s = 0.8 V\)。
解决方案
我们使用方程\ ref {peexpt} 来计算光电子的动能:
\[K_{max} = e\Delta V_s = e(0.80 V) = 0.80 \, eV. \nonumber \]
现在我们求解方程为\(\phi\):
\[\phi = hf - K_{max} = \frac{hc}{\lambda} - K_{max} = \frac{1240 \, eV \cdot m}{180 \, nm} − 0.80 \, eV = 6.09eV. \nonumber \]
最后,我们使用方程式求出截止频率:
\[f_c = \frac{\phi}{h} \frac{6.09 \, eV}{4.136 \times 10^{-15} eV \cdot s} = 1.47 \times 10^{-15} Hz. \nonumber \]
意义
在像本例所示的计算中,使用普朗克常数为单位比较方便,\(eV \cdot s\)并以 eV 而不是焦耳表示所有能量。
430 nm 紫光入射在功函数为 2.71 eV 的钙光电极上。 找出入射光子的能量和射出电子的最大动能。
策略
入射光子的能量就\(E_f = hf = hc/\lambda\)在我们使用的地方\(f\lambda = c\)。 为了获得喷射电子的最大能量,我们使用方程\ ref {6.16}。
解决方案
\[E_f = \frac{hc}{\lambda} = \frac{1240 \, eV \cdot nm}{430 \, nm} = 2.88 \, eV, \, K_{max} = E_f − \phi = 2.88 \, eV − 2.71 \, eV = 0.17 \, eV \nonumber \]
意义
在这个实验设置中,光电子在 0.17 V 的停止电位处停止流动。
589 nm 的黄色光入射在工作函数为 1.20 eV 的表面上。 制动潜力是什么? 截止波长是多少?
- 回答
-
\(-0.91 \, V\)1040 nm
某些材料中光电效应的截止频率为\(8.0×10^{13}Hz.\)当入射光的频率为时\(1.2×10^{14}Hz\),停止电位的测量值为 — 0.16 V。根据这些数据(以 j⋅sj·s 和 ev⋅sev·s 为单位)估算普朗克常数的值,然后确定你的误差百分比估计。
- 回答
-
\(h = 6.40 \times 10^{-34} J \cdot s = 4.0 \times 10^{-15} eV \cdot s\);\(-3.5\%\)


