4.6: 圆孔径和分辨率

Last updated
Save as PDF

Page ID: 201991

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

描述分辨率的衍射极限
描述光束传播的衍射极限

光线在空间中移动时会衍射，绕过障碍物弯曲，产生建设性和破坏性的干扰。它可以用作光谱工具——例如，衍射光栅根据波长分散光线，并用于产生光谱——但衍射也限制了我们在图像中获得的细节。

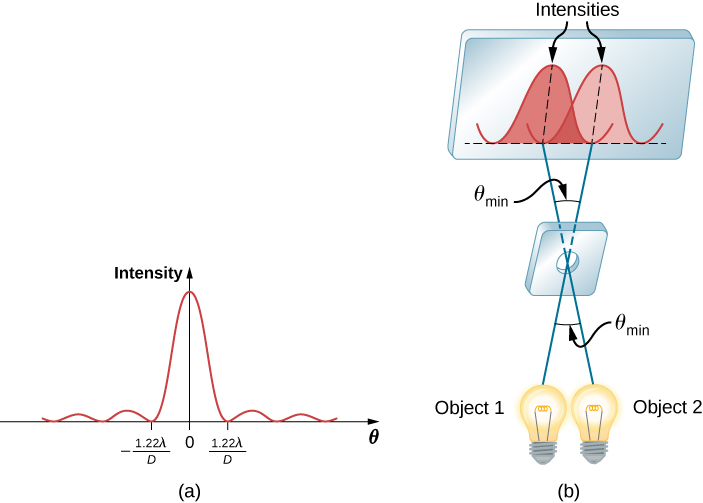
图中\(\PageIndex{1a}\)显示了光线穿过小圆孔的效果。我们得到的不是边缘锐利的亮点，而是边缘模糊的点，周围环绕着光圈。这种图案是由衍射引起的，类似于单个狭缝产生的衍射。来自圆形孔径不同部分的光会产生建设性和破坏性的干扰。当光圈较小时，效果最为明显，但大孔径也会产生这种效果。

图 a 在黑色背景上显示了一个明亮的白色圆圈。它的边缘是扩散的。图 b 和 c 显示两个重叠的白色圆圈。图 c 中的圆比图 b 中的圆更接近对方。 — 图\(\PageIndex{1}\)：(a) 穿过小圆孔的单色光会产生这种衍射图案。 (b) 两个彼此靠近的点光源由于衍射而产生重叠的图像。 (c) 如果来源距离更近，则无法区分或解决。

衍射如何影响光线穿过光圈时可以观察到的细节？图中\(\PageIndex{1b}\)显示了两个彼此靠近的点光源产生的衍射图案。这种模式与单点光源的模式类似，仍然可以分辨出有两个光源而不是一个。如果它们之间的距离更近，如图所示\(\PageIndex{1c}\)，我们就无法区分它们，从而限制了我们可以获得的细节或分辨率。这种极限是光的波浪性质的必然结果。

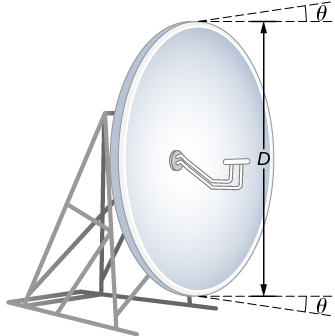
在许多情况下，衍射会限制分辨率。我们的视力受到限制，因为光线会穿过瞳孔，这是眼睛的圆形孔径。请注意，衍射般的光扩散是由于光束的直径有限，而不是与光圈的相互作用。因此，穿过具有直径的镜头的光会\(D\)显示出这种效果并扩散，使图像变得模糊，就像穿过直径光圈的光\(D\)一样。因此，衍射限制了任何带有镜头或反射镜的系统的分辨率。由于主镜的直径有限，望远镜也受到衍射\(D\)的限制。

限制到底是多少？要回答这个问题，可以考虑圆形孔径的衍射图案，其中心最大值比周围的最大值更宽更亮（类似于狭缝）（图\(\PageIndex{1a}\)）。可以看出，对于直径为的圆形孔径\(D\)，衍射图案中的第一个最小值出现在\(\theta = 1.22 \lambda/D\)（前提是孔径与光的波长相比要大，大多数光学仪器都是这种情况）。根据该角度确定分辨率衍射极限的公认标准被称为瑞利标准，该标准由瑞利勋爵在十九世纪提出。

瑞利标准

分辨率的衍射极限表明，当一张图像的衍射图案的中心直接高于另一张的衍射图案的第一个最小值时，两张图像才是可分辨的（图\(\PageIndex{1b}\)）。

第一个最小值的角度为\(\theta = 1.22 \lambda/D\)，因此，如果两个点物体被角度分开，则它们是可以解析的

\[\theta = 1.22 \dfrac{\lambda}{D} \label{Rayleigh} \]

其中\(λ\)是光（或其他电磁辐射）的波长，\(D\)是观察这两个物体的光圈、镜头、镜子等的直径。在此表达式中\(θ\)，以弧度为单位。这个角度通常也被称为衍射极限。

图 a 显示了强度与 theta 的对比图。它的中心有一个波峰，正负 1.22 lambda by D 处为零。图 b 显示了两个并排放置的灯泡。它们被标记为对象 1 和对象 2。来自两者的射线相互穿过，穿过交点方块中的一个洞。它们彼此形成一个角度 theta 下标最小值。光线落在另一侧的屏幕上。它们的强度在屏幕上显示为波浪。一个的波峰对应于另一个的零。 — 图\(\PageIndex{2}\)：(a) 圆形孔径的衍射图案强度图。请注意，与单个狭缝类似，中心最大值比侧面的最大值更宽更亮。 (b) 两个点物体产生重叠的衍射图案。这里显示的是可解析的 Rayleigh 标准。一个模式的中心最大值位于另一个模式的第一个最小值上。

所有观察物体大小和形状的尝试都受到探测器波长的限制。即使是小波长的光也无法实现精确的精度。当使用极小的波长探针时，例如使用电子显微镜，系统会受到干扰，这仍然限制了我们的知识。正如我们将在量子力学章节中看到的那样，海森堡的不确定性原理断言，这种极限是根本性的，不可避免的。

示例\(\PageIndex{1}\): Calculating Diffraction Limits of the Hubble Space Telescope

在轨道运行的哈勃太空望远镜的主镜直径为2.40米。在轨道上，该望远镜避免了大气失真对其分辨率的衰减影响。 (a) 两个刚刚可分辨的点光源（可能是两颗星）之间的角度是多少？假设平均光波长为 550 nm。 (b) 如果这两颗恒星的距离为 200 万光年，也就是仙女座星系的距离，那么它们之间的距离有多近，还能分辨出来？（光年或 ly 是指光在 1 年内传播的距离。）

策略

方程\ ref {Rayleigh} 中所述的瑞利标准给出了点源之间可能的最小角度 β 或最佳可获得的分辨率。\(\theta = 1.22 \lambda/D\) 一旦知道了这个角度，我们就可以计算出恒星之间的距离，因为我们可以得出它们有多远。

解决方案

最小可分辨角度的瑞利标准是\[\theta = 1.22 \dfrac{\lambda}{D}. \nonumber \]输入已知值给出\[\theta = 1.22\dfrac{550 \times 10^{-9} m}{2.40 \,m} = 2.80 \times 10^{-7} rad. \nonumber \]
距离为 r 的两个物体之间的距离 s，以一个角度 β 分隔\(s = r\theta\)。替换已知值可以得出\[s = (2.0 \times 10^6 \,ly)(2.80 \times 10^{-7} \,rad) = 0.56 \,ly. \nonumber \]

意义

(a) 部分中的角度非常小（小于 1/50,000 度），因为与光的波长相比，主镜太大了。如前所述，当光线与大小与光波长差不多的物体相互作用时，衍射效果最为明显。但是，效果仍然存在，可观察到的效果存在衍射极限。哈勃望远镜的实际分辨率不如这里发现的那么好。与所有仪器一样，还有其他影响，例如镜面不均匀或镜头像差进一步限制了分辨率。但是，由于哈勃的大小和质量，尤其是因为它位于地球大气层之上，因此该图\(\PageIndex{3}\)显示了哈勃可以观测到的细节范围。

图 a 和 b 显示了星系的望远镜图像。 — 图\(\PageIndex{3}\)：这两张 M82 Galaxy 的照片展示了使用（a）地面望远镜和（b）哈勃太空望远镜观察到的细节。（来源 a：“Ricnun” /Wikimedia Commons 对作品的修改）

第 (b) 部分的答案表明，相隔大约半光年的两颗恒星是可以分辨出来的。银河系中恒星之间的平均距离在外部约为五光年，在银河中心附近约为一光年。因此，哈勃可以解析仙女座星系中的大多数单颗恒星，尽管它距离如此之远，以至于它的光线需要200万年才能到达我们。图中\(\PageIndex{4}\)显示了另一面用于观测来自外太空的无线电波的镜子。

照片显示了很大的抛物线表面。 — 图\(\PageIndex{4}\)：波多黎各阿雷西博直径为305米的抛物线内衬反射材料，使其变成射电望远镜。它是世界上最大的曲面聚焦盘。尽管\(D\)对阿雷西博来说，它比哈勃望远镜大得多，但它探测到的辐射波长要长得多，其衍射极限明显低于哈勃望远镜的衍射极限。阿雷西博望远镜仍然非常有用，因为重要信息是由未携带的无线电波携带的通过可见光。（来源：杰夫·希区柯克）

练习\(\PageIndex{1}\)

图中所示的阿雷西博望远镜在 21 厘米波长下运行\(\PageIndex{4}\)时的角分辨率是多少？它与哈勃望远镜的分辨率相比如何？

回答: \(8.4 \times 10^{-4} \,rad\)，比哈勃望远镜宽 3000 倍

衍射不仅是光学仪器的问题，也是电磁辐射本身的问题。任何具有有限直径\(D\)和波长 λ的光束都表现出衍射扩散。光束以方程式\ ref {Rayleigh} 给出的角度 β 展开\(\theta = 1.22 \lambda/D\)。举个例子，由尽可能平行的射线构成的激光束（射线之间的角度尽可能接近 β = 0°）会以一定角度扩散\(\theta = 1.22 \lambda/D\)，其中\(D\)是光束的直径，λ是其波长。对于手电筒来说，这种扩散是不可能观察到的，因为它的光束一开始不是很平行。但是，对于激光束或微波信号的远距离传输，衍射扩散可能很大（图\(\PageIndex{5}\)）。为了避免这种情况，我们可以增加 D。这是为了向月球发射激光以测量其与地球的距离。激光束通过望远镜扩展，使激光束变得\(D\)更大更小。

图中显示了直径为 D 的碟形天线。从天线两边冒出的线与水平线形成一个角度 theta。 — 图\(\PageIndex{5}\)：\(\theta = 1.22 \lambda/D\)由于衍射，这种微波传输天线产生的波束以最小的角度展开。由于光束的直径有限，因此无法产生近乎平行的光束。

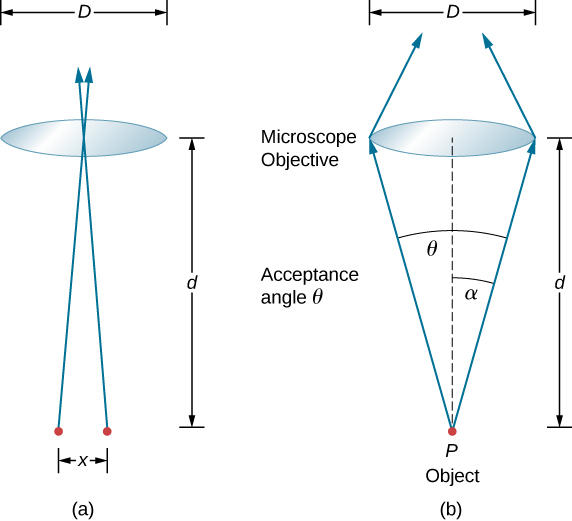
在大多数生物实验室中，引入显微镜的使用时，分辨率是一个问题。分离两个物体但仍被视为不同的距离 x 越小，分辨率就越高。镜头的分辨率定义为该距离 x。解析能力的表达式是从瑞利标准中获得的。 \(\PageIndex{6a}\)该图显示了以距离 x 分隔的两个点对象。根据瑞利标准，当最小角度间隔为时，分辨率是可能的

\[\theta = 1.22 \dfrac{\lambda}{D} = \dfrac{x}{d}, \nonumber \]

哪里\(D\)是标本和物镜之间的距离，我们使用了小角度近似值（即，我们假设 x 比 d 小得多），所以\(tan \,\theta \approx sin \,\theta\)。因此，决心力是

\[x= 1.22 \dfrac{\lambda d}{D}. \nonumber \]

另一种看待这个问题的方法是使用数值孔径（NA）的概念，它是衡量镜头吸收光线并仍将其包含在镜头内的最大接受角度。图中\(\PageIndex{1b}\)显示了 P 点处的镜头和物体。这里的 NA 是衡量镜头收集光线和分辨精细细节能力的指标。镜头在聚焦时所承受的角度定义为\(\theta = 2\alpha\)。从图中再用小角度近似值，我们可以这样写

\[sin \,\alpha = \dfrac{D/2}{d} = \dfrac{D}{2d}. \nonumber \]

镜头的 NA 为\(NA = n \,sin \,\alpha\)，其中 n 是物镜和物体之间介质在 P 点处的折射率。从这个对 NA 的定义中，我们可以看出

\[x = 1.22 \dfrac{\lambda d}{D} = 1.22 \dfrac{\lambda}{2 \,sin \,\alpha} = 0.61 \dfrac{\lambda n}{NA}. \nonumber \]

在显微镜中，NA 很重要，因为它与镜头的分辨率有关。具有较大 NA 的镜头能够分辨更精细的细节。 NA 较大的镜头也能够收集更多的光线，从而提供更明亮的图像。描述这种情况的另一种方法是，NA 越大，可以带入镜头的光锥越大，因此收集的衍射模式越多。因此，显微镜具有更多的信息以形成清晰的图像，并且其分辨率更高。

图 a 显示了相距 d 的两个点。光线从这些点发出，在距离点 d 的距离处相互相交。在交点处放置直径为 D 的透镜。图 b 显示了一个标记为 P 的点，对象。两条光线从这里发出，击中镜头的两端。它们与中心轴形成一个角度 alpha，彼此形成一个角度 theta。 Theta 是接受角度。镜头被标记为微观物镜。光线在镜头的另一侧相互向后移动。 — 图\(\PageIndex{6}\)：(a) 两点间隔一段距离 x，位置\(D\)距离物镜有一段距离。 (b) 讨论镜头和物体在 P 点的分辨力时使用的术语和符号（来源 a：“Infopro” /Wikimedia Commons 对作品的修改）。

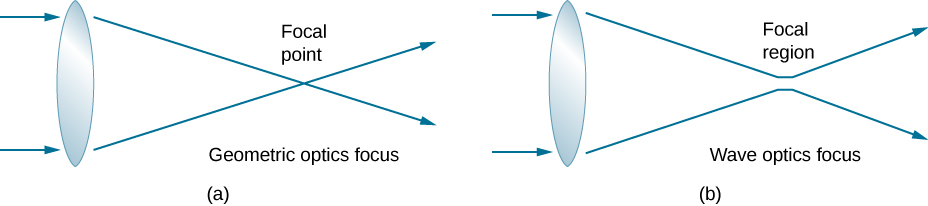
衍射的后果之一是光束的焦点具有有限的宽度和强度分布。想象一下，只考虑几何光学时聚焦，如图所示\(\PageIndex{7a}\)。焦点被认为是一个无限小的点，强度很大，能够焚烧大多数样品，无论物镜镜的 NA 如何，这在物理上都过于简单化。对于波动光学，由于衍射，我们考虑了焦点扩散成为焦点的现象（图\(\PageIndex{7b}\)），光斑的大小随北美的增加而减小。因此，焦点的强度随着 NA 的增加而增加。 NA 越高，对标本进行光降解的机会就越大。但是，这个地方永远不会成为真实点。

图 a 和 b 显示两条光线从左侧进入镜头。在图 a 中，光线出现在右侧并在焦点处相互相交。这被标记为几何光学焦点。在图 b 中，光线出现，相互移动，但不相交。它们最接近的区域被标记为焦点区域。光线从这里发散。这被标记为波动光学焦点。 — 图\(\PageIndex{7}\) :( a) 在几何光学中，焦点被建模为一个点，但物理上不可能产生这样的点，因为它意味着无限的强度。 (b) 在波动光学中，焦点是延伸区域。

在另一种类型的显微镜中，样本中的分子通过一种称为荧光的机制发光。通过控制发光的分子，可以构建分辨率比瑞利标准高得多的图像，从而绕过衍射极限。超分辨率荧光显微镜的开发促成了2014年诺贝尔化学奖。

光学分辨率模拟

在这个光学分辨率模型中，Fu-Kun Hwang的仿真中并排显示了通过两个圆孔的光的两种衍射图案。当你减小孔径时，观察图案的合并。