Skip to main content
Global

4.5: 衍射光栅

  1. Last updated
  2. Save as PDF
  • Page ID
    201987

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 讨论从衍射光栅获得的图案
    • 解释衍射光栅的效果

    分析光线穿过两个狭缝的干扰确定了干扰的理论框架，并让我们对托马斯·杨的实验有了历史见解。 但是，大多数现代狭缝干扰应用不仅使用两个狭缝，还使用许多狭缝，出于实际目的接近无穷大。 关键光学元件称为衍射光栅，是光学分析中的重要工具。

    衍射光栅：无限数量的狭缝

    对 “干扰” 中多缝干扰的分析使我们能够考虑当狭缝 N 的数量接近无穷大时会发生什么。 回想一下，\(N - 2\)次要最大值出现在主最大值之间。 我们可以看到会出现无限数量的次要最大值，它们之间会有无限数量的深色条纹。 这使得条纹之间的间距，从而使最大值的宽度变得无限小。 此外，由于次要最大值的强度与成正比\(1/N^2\)，因此它接近于零，因此无法再看到次要最大值。 剩下的只是主最大值，现在非常明亮而且非常狭窄（图\(\PageIndex{1}\)）。

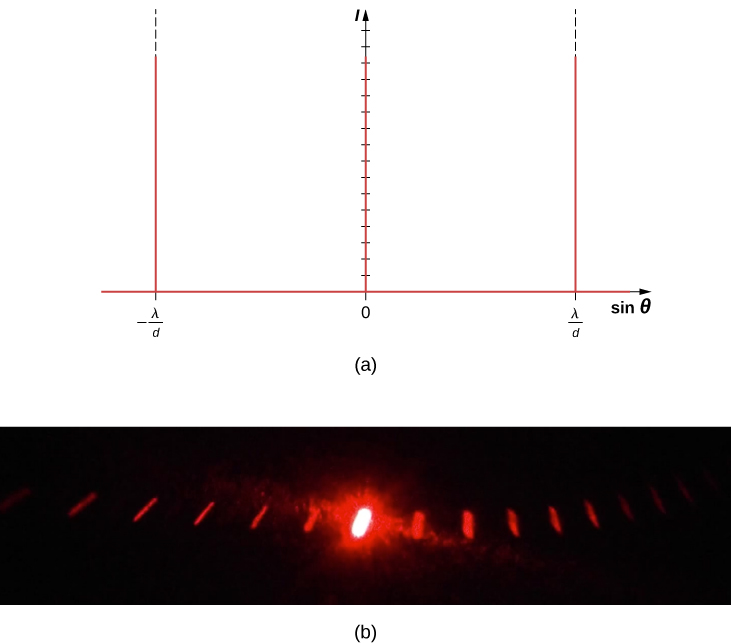
    图 a 显示了 I 与正弦西太的对比图。 它有两条垂直线在 sine theta 处等于 lambda x D 和减去 lambda by D。图 b 在中间的黑色背景上显示了一个鲜红色的斑点。 它的两侧都被逐渐变暗的斑点所环绕，向外延伸。
    图\(\PageIndex{1}\)：(a) 透过大量狭缝的光强度。 当 N 接近无穷大时，只有主最大值保持为非常明亮和非常窄的线。 (b) 穿过衍射光栅的激光束。 （来源 b：塞巴斯蒂安·斯塔佩尔伯格对作品的修改）

    实际上，狭缝的数量不是无限的，但它可以非常大，足以产生等效的效果。 一个典型的例子是称为衍射光栅的光学元件。 衍射光栅可以通过使用锋利的工具在大量精确定位的平行线上雕刻玻璃来制成，未触及的区域就像狭缝一样（图\(\PageIndex{2}\)）。 这种类型的光栅可以以相当便宜的价格通过摄影批量生产。 由于光栅每毫米可以有 1000 多条线，因此当入射光线照亮小至几毫米的部分时，照明狭缝的数量实际上是无限的，从而提供了非常清晰的主最大值。

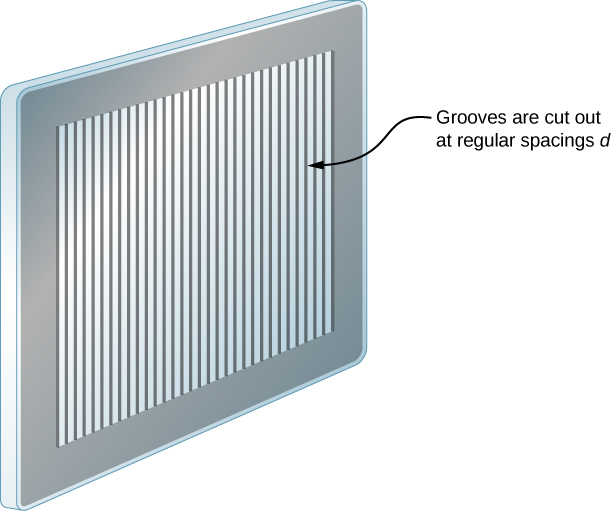
    该图显示了一个带有细而平行凹槽的矩形扁平块。 凹槽以规则间距切开 d.
    图\(\PageIndex{2}\)：衍射光栅可以通过用锋利的工具在大量精确定位的平行线上雕刻玻璃来制成。

    衍射光栅既可以传输光，如图所示\(\PageIndex{3}\)，也可以用于光的反射，如蝴蝶翅膀和图中的澳大利亚蛋白石\(\PageIndex{4a}\)。 自然衍射光栅也出现在某些鸟类的羽毛中，例如蜂鸟。 规则图案中的微小手指状结构充当反射光栅，产生构造干扰，使羽毛的颜色不仅仅是因为它们的色素沉着。 这被称为虹彩。

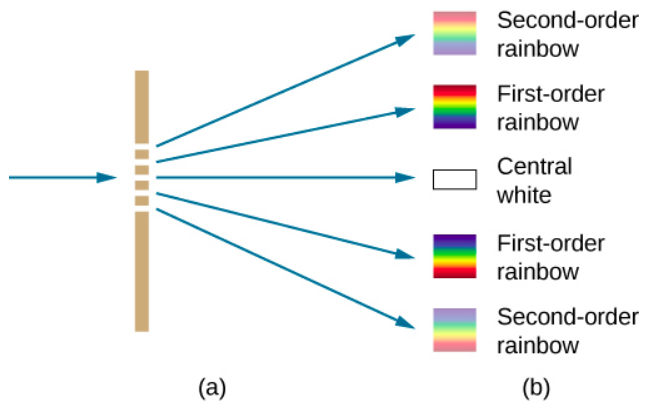
    该图显示了左侧的一条垂直线。 它有五个凹槽。 一条射线从左进入，五条光线从右边冒出来，每个凹槽中有一条。 它们指向从上到下被标记的正方形：二阶彩虹、一阶彩虹、中央白色、一阶彩虹、二阶彩虹。 方块中显示的第一阶彩虹比二阶彩虹亮。
    图\(\PageIndex{3}\)：(a) 穿过衍射光栅的光以类似于双缝的图案进行衍射，亮区分布在不同的角度。 (b) 白光入射在光栅上获得的图案。 中心最大值为白色，高阶最大值将白光分散成彩虹色。
    图 a 是一张反映各种颜色的蛋白石吊坠的照片。 图 b 是一只蝴蝶的照片。
    图\(\PageIndex{4}\)：（a）这只澳大利亚蛋白石和（b）蝴蝶翅膀有成排的反射镜，其作用类似于反射光栅，以不同的角度反射不同的颜色。 （来源 a：修改 “Opals-On-Black” /Flickr 的作品；来源 b：“whologwh” /Flickr 对作品的修改）

    衍射光栅的应用

    衍射光栅在应用中用在哪里？ 衍射光栅通常用于光谱色散和光分析。 它们之所以特别有用，是因为它们形成了比双缝更清晰的图案。 也就是说，它们的明亮条纹越来越窄更亮，而它们的暗区更暗。 衍射光栅是单色器的关键组件，例如，用于对来自生物或医学样品的特定波长的光学成像。 可以选择衍射光栅来专门分析活检样品中病变细胞中的分子发射的波长，或者用选定的光波长帮助激发样品中的战略分子。 另一个重要用途是光纤技术，在这种技术中，光纤的设计目的是在特定波长下提供最佳性能。 一系列衍射光栅可用于选择用于此类用途的波长。

    示例\(\PageIndex{1}\): Calculating Typical Diffraction Grating Effects

    每厘米有 10,000 条线的衍射光栅随时可用。 假设你有一个，然后你通过它向2.00米外的屏幕发出一束白光。

    1. 找到最短和最长可见光波长（分别为 380 和 760 nm）的一阶衍射角度。
    2. 屏幕上产生的用于一阶干扰的可见光彩虹两端之间的距离是多少？ （图\(\PageIndex{5}\)）。
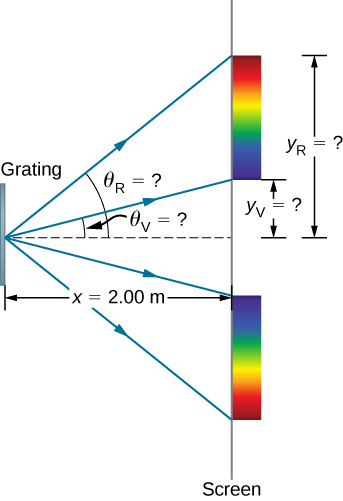
    3. 左边的垂直线标记为光栅，右边的一条竖线标为屏幕。 它们的距离 x 等于 2 米的距离。 四个箭头从光栅辐射到屏幕。 从顶部开始的第一个和第二个分别与中心轴成了 theta R 和 theta V 的角度。 它们落在屏幕上的点分别位于距中心轴线的 yR 和 yV 的距离。 彩虹在屏幕上第一和第二箭头之间以及第三和第四箭头之间形成。
      图\(\PageIndex{5}\)：(a) 本例中考虑的衍射光栅在距离光栅一定\(x = 2.00 \, m\)距离的屏幕上产生彩虹色彩。 屏幕上的距离是垂直于 x 方向测量的。 换句话说，彩虹图案从页面外延伸。

    (b) 在鸟瞰图中，在放置装备的桌子上可以看到彩虹图案。

    策略

    一旦确定了衍射光栅狭缝\(d\)间距的值，就可以使用方程找到锐线的角度

    \[d \, \sin \, \theta = m\lambda \nonumber \]

    对于\(m = 0, \pm1, \pm2, ... \)。

    由于每厘米有 10,000 条线，因此每条线之间以 1/10,000 厘米分隔。 一旦我们知道了角度，我们就可以使用简单的三角函数找到屏幕上的距离。

    解决方案
    1. 狭缝之间的距离为\(d = (1 \, cm)/10,000 = 1.00 \times 10^{-4} \, cm\)或\(1.00 \times 10^{-6} m\)。 让我们把这两个角度\(\theta_V\)称为紫罗兰色（380 nm）和\(\theta_R\)红色（760 nm）。 求解方\(d \, \sin \theta_V = m\lambda\)程\(\sin \, \theta_V\)为

      \[\sin \, \theta_V = \frac{m\lambda_V}{d},\nonumber \]

      其中 m = 1 表示一阶和\(\lambda_V = 380 \, nm = 3.80 \times 10^{-7}m\)。 用这些值代替可以得到

      \[\sin \, \theta_V = \frac{3.80 \times 10^{-7}m}{1.00 \times 10^{-6}m} = 0.380.\nonumber \]

      因此，角度\(\theta_V\)为

      \[\theta_V = \sin^{-1} 0.380 = 22.33°.\nonumber \]

      同样，

      \[\sin \, \theta_R = \frac{7.60 \times 10^{-7}m}{1.00 \times 10^{-6}m} = 0.760.\nonumber \]

      因此，角度\(\theta_R\)为

      \[\theta_R = \sin^{-1} 0.760 = 49.46°. \nonumber \]

      请注意，在两个方程中，我们将这些中间计算的结果报告为四个重要数字，用于 (b) 部分的计算。
    2. 屏幕上的距离标有标签\(y_V\)，如图\(y_R\)所示\(\PageIndex{5}\)。 请注意\(tan \, \theta = y/x\)。 我们可以为 and 求\(y_V\)解\(y_R\)。 也就是说，

      \[y_V = x \, \tan \, \theta_V = (2.00 \, m)(\tan \, 22.33°) = 0.815 \, m \nonumber \]

      和

      \[y_R = x \, \tan \, \theta_R = (2.00 \, m)(\tan \, 49.46°) = 2.338 \, m. \nonumber \]

      因此，它们之间的距离是

      \[y_R - y_V = 1.523 \, m \nonumber \]

    意义

    由白光产生的彩虹的红色和紫色两端之间的距离很远，这表明这种衍射光栅作为光谱工具具有潜力。 它能分散的波长越多（色散越大），在光谱中可以看到的细节就越多。 这取决于衍射光栅的质量——除了要有紧密间隔的线条外，还必须非常精确地制作。

    练习\(\PageIndex{1}\)

    如果不能精确知道衍射光栅\(d\)的线距，我们可以使用波长明确的光源进行测量。 假设氢气\(H_{\beta}\)发射线 (\(\lambda = 656.3 \, nm\)) 的一阶构造条纹是使用带有衍射光栅的光谱仪在 11.36° 下测量的。 这个光栅的线间距是多少？

    回答

    \(3.332 \times 10^{-6} m\)或每毫米 300 行

    采用我们用于双缝衍射的相同模拟，并尝试将狭缝的数量从增加\(N = 2\)到\(N = 3, 4, 5, ...\)。 主峰变得越来越尖锐，次要峰变得越来越不明显。 当你达到最大数量时\(N = 20\)，系统的行为就像衍射光栅一样。