4.7: X 射线衍射

Last updated
Save as PDF

Page ID: 202005

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

描述 X 射线与原子尺度结构相互作用时表现出的干扰和衍射效应

由于 X 射线光子能量很高，因此它们的波长相对较短，大约在\(10^{-8}\) m 到\(10^{-12}\) m 之间。因此，典型的 X 射线光子在遇到宏观物体（如牙齿）时就像射线一样，产生尖锐的阴影。但是，由于原子的大小约为 0.1 nm，因此可以使用 X 射线来检测原子和分子的位置、形状和大小。这个过程被称为 X 射线衍射，它涉及 X 射线的干扰以产生图案，这些图案可以进行分析，以获取有关散射 X 射线的结构的信息。

也许最著名的X射线衍射例子是1953年在英格兰卡文迪许实验室工作的一个国际科学家小组发现了 DNA 的双螺旋结构，他们是美国人詹姆斯·沃森、英国人弗朗西斯·克里克和出生于新西兰的莫里斯·威尔金斯。他们利用罗莎琳德·富兰克林产生的X射线衍射数据，率先对生命至关重要的DNA双螺旋结构进行建模。由于这项工作，沃森、克里克和威尔金斯获得了1962年诺贝尔生理学或医学奖。（关于罗莎琳德·富兰克林没有被列入该奖项的问题存在一些争论和争议，尽管她于1958年在获奖前去世。）

该图\(\PageIndex{1}\)显示了晶体的 X 射线散射产生的衍射图案。这个过程被称为X射线晶体学，因为它可以产生有关晶体结构的信息，而这是罗莎琳德·富兰克林提供给沃森和克里克的DNA数据类型。 X 射线不仅可以确认原子的大小和形状，还可以提供有关材料中原子排列的信息。例如，最近对高温超导体的研究涉及复杂材料，这些材料的晶格排列对于获得超导材料至关重要。这些可以通过X射线晶体学进行研究。

该图显示了带有黑色虚线图案的白色背景。中间有一个明亮的白色斑点，周围环绕着一个灰色的环。一条白线从现场向上和向左移动。 — 图\(\PageIndex{1}\)：来自蛋白质（母鸡蛋溶菌酶）晶体的 X 射线衍射产生了这种干扰模式。对模式的分析会产生有关蛋白质结构的信息。（来源：“Del45” /维基共享资源）

从历史上看，来自晶体的X射线的散射被用来证明X射线是高能电磁（EM）波。自1895年发现X射线以来，人们就怀疑这一点，但直到1912年，德国人马克斯· 冯·劳伊（1879—1960）才说服他的两位同事从晶体中散射X射线。他推理说，如果获得衍射图案，那么 X 射线必须是波浪，其波长是可以确定的。（根据阿沃加德罗数的良好值，当时各种晶体中原子的间距已相当广为人知。）这些实验令人信服，1914年诺贝尔物理学奖被授予冯·劳伊，因为他的建议证明了X射线是电磁波。 1915 年，威廉·亨利·布拉格爵士和他的儿子威廉·劳伦斯· 布拉格爵士组成的独一无二的父子团队因发明了 X 射线光谱仪和当时新的 X 射线分析科学而获得诺贝尔联合奖。

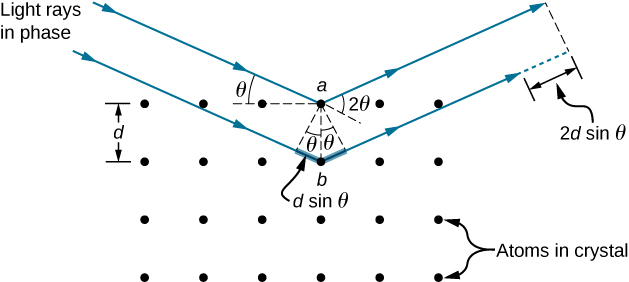
以让人联想到薄膜干扰的方式，我们考虑的是两个采用 X 射线波长的平面波，每个平面波从晶格内的不同原子平面反射，如图所示\(\PageIndex{2}\)。从几何学来看，路径长度的差异是\(2d \, \sin \, \theta\)。当该距离是波长的整数倍时，就会产生构造干扰。这个条件由布拉格方程捕获，

\[m\lambda = 2d \, \sin \, \theta,\label{Bragg} \]

对于\(m = 1,2,3, ...\)。

其中\(m\)是正整数，\(d\)是平面之间的间距。根据反射定律，入射波和反射波都是用相同的角度描述的\(θ\)，但与几何光学的一般做法不同，入射波和反射波\(θ\)是根据表面本身而不是法线来测量的。

该图将晶体中的原子显示为网格中排列的点。它们彼此之间有一段距离 d。两条平行光线，相位标记为光线，分别从上和向左撞击一个原子，偏转，然后向上和向右移动。有关原子被标记为 a 和 b，b 在 a 的正下方。入射射线与水平线形成一个角度 theta。它们的延伸部分与偏转的光线形成20度的角度。一条虚线连接 a 和 b。另一条虚线将 a 与入射在 b 上的射线相连，与 ab 形成一个角度 theta，从而形成一个三角形。三角形沿射在 b 上的射线的一侧被标记为 d sine theta。从 b 偏转的光线小于从 a 偏转的光线，距离为 2d sine theta。 — 图\(\PageIndex{2}\)：用晶体进行 X 射线衍射。两个入射波从晶体的两个平面上反射。路径长度的差异由虚线表示。

示例\(\PageIndex{1}\): X-Ray Diffraction with Salt Crystals

普通食盐主要由\(\ce{NaCl}\)晶体组成。在\(\ce{NaCl}\)晶体中，有一系列相距 0.252 nm 的平面。如果在 18.1° 的入射角下观察到一阶最大值，那么该晶体的 X 射线散射波长是多少？

策略：

使用布拉格方程式\ ref {Bragg} 求解\(θ\)。

解决方案

对于一阶和\(m = 1\)，平面间距\(d\)是已知的。求解布拉格方程以获得波长会产生

\[\begin{align*} \lambda &= \dfrac{2d \, \sin \, \theta}{m} \\[4pt] &= \dfrac{2(0.252 \times 10^{-9} m) \, \sin \, (18.1^o)}{1} \\[4pt] &= 1.57 \times 10^{-10} m, \, or \, 0.157 \, nm \end{align*} \nonumber \]

意义

确定的波长适合电磁频谱的X射线区域。再一次，当光的波长 () 与它相互作用的物理结构 (\(\lambda = 0.157 \, nm\)\(d = 0.252 \, nm\)) 的大小相似时，光的波浪性质就会变得突出。

练习\(\PageIndex{1}\)

对于示例中描述的实验\(\PageIndex{1}\)，可以观察到干扰最大值的另外两个角度是什么？什么限制了最大值的数量？

回答: \(38.4^o\)和\(68.8^o\); 之间\(\theta = 0^o \rightarrow 90^o\)，顺序 1、2 和 3 都是存在的。

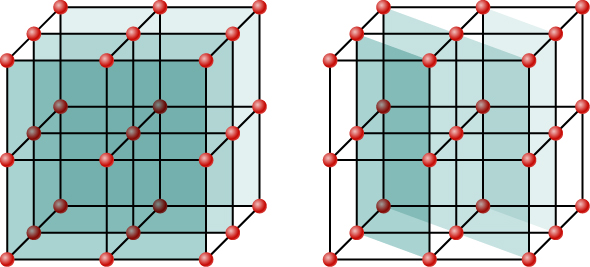
尽管为了简单起见，图中将晶体\(\PageIndex{2}\)描绘成散射中心的二维阵列，但真正的晶体是三维结构。散射可以同时发生在不同方向和间距模式的不同平面族上，称为布拉格平面，如图所示\(\PageIndex{3}\)。由此产生的干扰模式可能非常复杂。

图中显示了两个晶格，原子显示为小圆圈，通过线条相互连接。在第一个晶格中，突出显示在晶格中形成的平面。在第二张图中，突出显示了在晶格中形成的倾斜平面。在每种情况下，平面都被视为同一个晶格中不同原子的组合。 — 图\(\PageIndex{3}\)：由于形成晶体结构的规律性，一个晶体在其几何形状中可以有许多系列的平面，每个平面都会产生 X 射线衍射。