Skip to main content
Global

4.3：单缝衍射中的强度

  1. Last updated
  2. Save as PDF
  • Page ID
    202004

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 计算相对于单缝衍射峰的中心最大值的强度
    • 计算相对于屏幕上任意点的中心最大值的强度

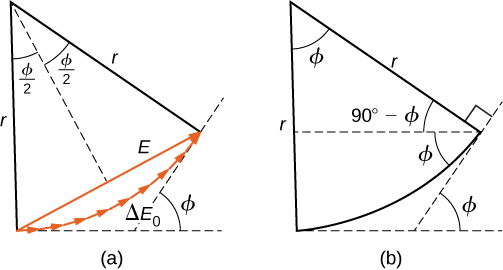
    为了计算衍射图案的强度，我们遵循交流电路中用于计算交流电路的相量方法。 如果我们认为前面所示的狭缝上有\(N\)惠更斯来源，每个源与其相邻的邻居相隔一定距离 A/n，则来自相邻源的波浪到达屏幕\(P\)上任意点之间的路径差为\((a/N) \, \sin \theta\)。 此距离等于相位差为\((2\pi a/\lambda N) \, \sin \, \theta\)。 到达角度位置所在点的波浪的相量\(\theta\)图如图所示\(\PageIndex{1}\)。 每个惠更斯小波的相量振幅为\(\Delta E_0\)，合成相量的振幅为\(E\)，来自第一个源和最后一个源的小波之间的相位差为

    \[\phi = \left(\dfrac{2\pi}{\lambda}\right) \, a \, \sin \theta. \nonumber \]

    使用\(N → ∞\)，相量图接近长\(N \Delta E_0\)度和半径的圆弧\(r\)。 由于弧的长度\(N \Delta E_0\)适用于任何\(ϕ\)，因此弧\(r\)的半径必须随着\(ϕ\)增加而减小（或者等效地，因为相量形成更紧的螺旋）。

    图 a 显示了一条弧线，其相量标记为 delta E 下标 0。 这会通过两条标有 r 的直线在圆心处减去一个角度。这个角度被一分为二，每半都用 phi 标记 2。 弧的端点通过标有 E 的箭头连接。弧线一个端点的切线是水平的。 圆弧另一端的切线与水平线成了 phi 的角度。 图 b 显示了弧线及其对应的角度 phi。 虚线从弧线的一个端点延伸到相反的直线 r。它与 r 垂直。它与弧线成一个角度 phi，与相邻的线 r 形成一个角度 90 减去 phi。
    图\(\PageIndex{1}\)：(a) 对应于单缝衍射图案中角度位置 β 的相量图。 来自第一个源和最后一个源的小波之间的相位差为\(\phi = (2\pi /\lambda)a \, sin \, \theta\)。 (b) 相量图的几何形状。

    图中\(\PageIndex{1a}\)使用 N=30 显示了 = 0（衍射图案的中心）的相量图。 在这种情况下，相量在一条长度的直线上端到端放置\(N \Delta E_0\)，半径 r 变为无穷大，结果具有其最大值\(E = N\Delta E_0\)。 光的强度可以使用电磁波的关系\(I = \dfrac{1}{2} c \epsilon_0 E^2\)获得。 然后，最大值的强度为

    \[I_0 = \dfrac{1}{2} c\epsilon_0 (N \Delta E_0)^2 = \dfrac{1}{2\mu_0 c}(N\Delta E_0)^2, \nonumber \]

    哪里\(\epsilon_0 = 1/\mu_0 c^2\)。 衍射图案前两个零的相量图如图\(\PageIndex{1b}\)和图所示\(\PageIndex{1d}\)。 在这两种情况下，在旋转 rad 表示 m = 1 和\(\phi = 2\pi\)\(4 \pi\) rad 表示 m = 2 之后，相量加为零。

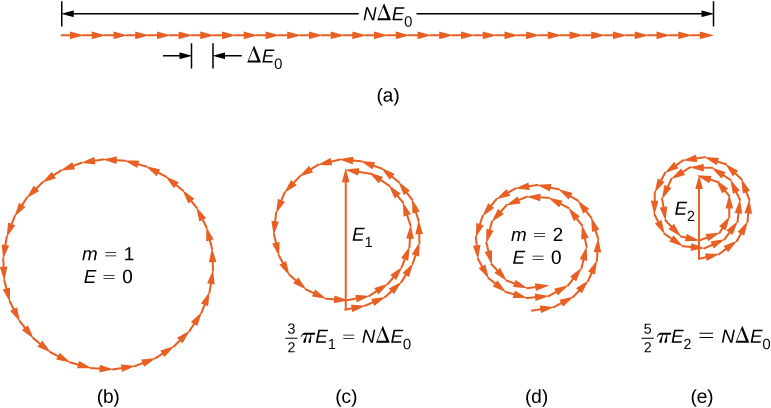
    图 a 显示了一行长度为 N delta E 下标 0 的 30 个相量。 相量的长度为 delta E 下标 0。 图 b 显示了一个圆圈，其中相量指向逆时针方向。 这被标记为 m 等于 1，E 等于 0。 图 c 显示了沿圆形的相量。 它们从底部开始，沿逆时针方向绕圆圈走一圈半。 从起点到终点的箭头标有 E1。 它形成了圆的直径。 图 c 被标记为 3 乘以 2 pi E1 等于 N delta E0。 图 d 显示了沿圆形的相量。 它们从底部开始，沿逆时针方向绕圆圈走两次。 该图标为 m 等于 2，E 等于 0。 图 e 显示了沿圆形的相量。 它们从底部开始，沿逆时针方向绕圆圈移动两次半。 从起点到终点的箭头标有 E2。 它形成了圆的直径。 图 c 被标记为 5 x 2 pi E2 等于 N delta E0。
    图\(\PageIndex{2}\)：单缝衍射图案上各个点的相量图（含有 30 个相量）。 围绕给定圆圈的多次旋转已稍微分开，因此可以看到相量。 (a) 中心最大值，(b) 第一个最小值，(c) 超出中心最大值的第一个最大值，(d) 第二个最小值，以及 (e) 超出中心最大值的第二个最大值。

    除中心最大值之外的接下来的两个最大值由部分 (c) 和 (e) 的相量图表示。 在 (c) 部分中，相量在\(\phi = 3\pi\) rad 中旋转并形成了由此产生的量级相量\(E_1\)。 由相量形成的电弧的长度为\(N\Delta E_0\)。 由于这相当于围绕一个直径圆旋转 1.5 次\(E_1\)，所以我们有

    \[\dfrac{3}{2} \pi E_1 = N \Delta E_0, \nonumber \]

    所以

    \[E_1 = \dfrac{2N\Delta E_0}{3\pi} \nonumber \]

    和

    \[I_1 = \dfrac{1}{2\mu_0 c}E_1^2 = \dfrac{4(N\Delta E_0)^2}{(9\pi^2)(2\mu_0c)} = 0.045 I_0, \nonumber \]

    哪里

    \[I_0 = \dfrac{(N\Delta E_0)^2}{2\mu_0 c}. \nonumber \]

    在 (e) 部分中，相量在\(\phi = 5\pi\) rad 中旋转，相当于围绕直径\(E_2\)和弧长的圆旋转 2.5 次\(N\Delta E_0\)。 这导致\(I_2 = 0.016 I_0\). 证明留给学生做练习（练习 4.119）。

    这两个最大值实际上对应于略小于\(3\pi\) rad 和\(5\pi\) rad 的值。 由于相量图的弧的总长度始终为\(N \Delta E_0\)，因此弧的半径会随着\(ϕ\)增加而减小。 因此，事实证明，\(E_1\)对于尚未完全卷曲穿过\(3\pi\) rad 和\(5\pi\) rad 的弧线，结果会稍大一些。\(E_2\) 练习 4.120 中研究了最大值的确切值。\(ϕ\) 在解决这个问题时，你会发现它们小于，但非常接近\(\phi = 3\pi, \, 5\pi, \, 7\pi,\)... rad。

    要计算屏幕\(P\)上任意点的强度，我们返回到图中的相量图\(\PageIndex{1}\)。 由于弧线在圆心处逆转一个角度，

    \[N\Delta E_0 = r\phi \label{eq10} \]

    和

    \[\sin \left(\dfrac{\phi}{2}\right) = \dfrac{E}{2r}. \label{eq11} \]

    其中\(E\)是合成场的振幅。 我们发现，求解方程\ ref {eq11}\(E\) 然后用方\(r\)程\ ref {eq10} 代替

    \[\begin{align*} E &= 2r \, \sin \, \dfrac{\phi}{2} \\[5pt] &= 2\dfrac{N\Delta E_0}{\phi} \sin \, \dfrac{\phi}{2}. \end{align*} \nonumber \]

    现在正在定义

    \[\beta = \dfrac{\phi}{2} = \dfrac{\pi a \, \sin \, \theta}{\lambda} \label{4.2} \]

    我们得到

    \[E = N\Delta E_0 \dfrac{\sin \, \beta}{\beta} \label{eq15} \]

    方程\ ref {eq15} 将衍射图案中任一点合成场的振幅与中心最大值的振幅\(N \Delta E_0\)联系起来。 强度与振幅的平方成正比，所以

    \[I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 \label{eq20} \]

    其中\(I_0 = (N\delta E_0)^2/2\mu_0 c\)是图案中心的强度。

    对于中心最大值，= 0，β 也为零，我们从 l'Hôpital 的规则中可以看出\(\lim_{\beta \rightarrow 0}(sin \, \beta/\beta) = 1\)，就是这样\(lim_{\phi \rightarrow 0}I = I_0\)。 对于下一个最大值\(\phi = 3\pi\) rad，我们有\(\beta = 3\pi/2\) rad，当代入方程\ ref {eq20} 时，它会产生

    \[I_1 = I_0 \left(\dfrac{\sin \, 3\pi/2}{3\pi/2}\right)^2 = 0.045 I_0, \nonumber \]

    这与我们在本节前面使用相量图的直径和周长发现的结果一致。 将\(\phi = 5\pi\) rad 代入方程\ ref {eq20} 会得到类似的结果\(I_2\)。

    方程\ ref {eq20} 的曲线如图\(\PageIndex{3}\)所示，其正下方是实际衍射图案的照片。 请注意，中心峰比其他峰亮得多，并且图案的零位于\(\beta = m\pi\)读取时出现的那些点。\(sin \, \beta = 0\) 这对应于

    \[\dfrac{\pi a \, \sin \theta}{\lambda} = m\pi, \nonumber \]

    要么

    \[a \, \sin \, \theta = m \lambda, \nonumber \]

    这是我们之前因破坏性干扰或单个缝隙而得出的。

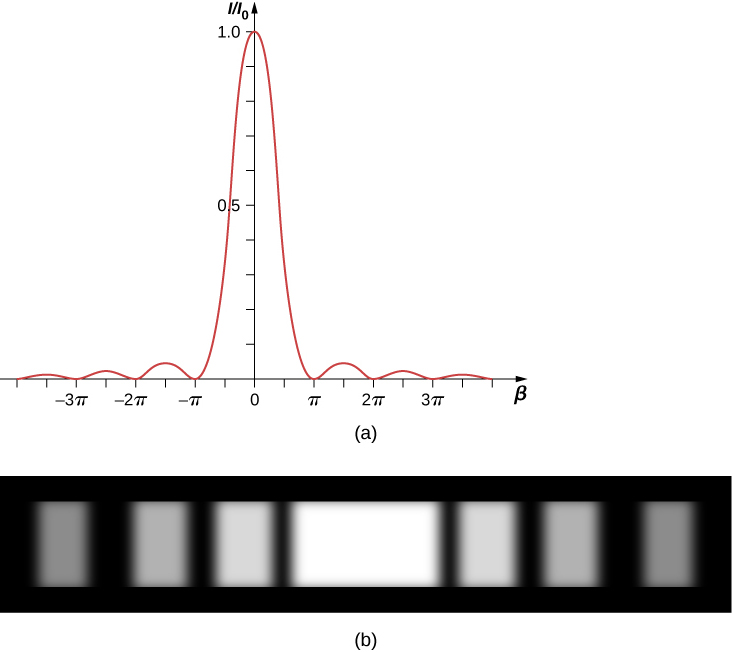
    图 a 显示了 I by I0 与 beta 的对比图。 在 beta 时，图表中心有一个波峰，等于 0。 它的 y 值为 1。 这张图的两边都有波纹，当你向外走时，波纹会变小。 该图在负 3 pi、负 2 pi、负 pi、pi、2 pi、3 pi 处为零。 图 b 显示了亮区和暗区交替出现的条带。 中央部分最亮。
    图\(\PageIndex{3}\)：(a) 计算出的单缝衍射图案的强度分布。 (b) 实际的衍射图案。
    示例\(\PageIndex{1}\): Intensity in Single-Slit Diffraction

    波长为 550 nm 的光穿过宽度为 2.00 μm 的狭缝，产生类似于图中所示的衍射图案\(\PageIndex{3a}\)。

    1. 根据与中心最大值之间的角度找出前两个最小值的位置。
    2. 在这两个最小值之间的中间点确定相对于中心最大值的强度。

    策略

    最小值由方程 4.2.1 给出\(a \, sin \, \theta = m\lambda\)。 前两个最小值为 m = 1 和 m = 2。 计算出角度后，方程\ ref {eq20} 和方程\ ref {4.2} 可用于确定强度。

    解决方案
    1. 求解 β 的方程 4.2.1 可以给我们\(\theta_m = \sin^{-1}(m\lambda/a)\)，所以

      \[\theta_1 = \sin^{-1} \left(\dfrac{(+1)(550 \times 10^{-9} m)}{2.00 \times 10^{-6}m}\right) = +16.0° \nonumber \]

      和

      \[\theta_2 = \sin^{-1} \left(\dfrac{(+2)(550 \times 10^{-9}m)}{2.00 \times 10^{-6}m}\right) = +33.4°. \nonumber \]

    2. \(\theta_1\)和之间的中间点\(\theta_2\)是

      \[\theta = (\theta_1 + \theta_2) /2 = (16.0° + 33.4°)/2 = 24.7°. \nonumber \]

    方程\ ref {4.2} 给出

    \[\beta = \dfrac{\pi a \, sin \, \theta}{\lambda} = \dfrac{\pi (2.00 \times 10^{-6}m) \, \sin \, (24.7°)}{(550 \times 10^{-9}m)} = 1.52\pi \, or \, 4.77 \, rad. \nonumber \]

    根据方程\ ref {eq20}，我们可以计算

    \[\dfrac{I}{I_0} = \left(\dfrac{\sin \, \beta}{\beta}\right)^2 = \left(\dfrac{\sin \, (4.77)}{4.77}\right)^2 = \left(\dfrac{-0.9985}{4.77}\right)^2 = 0.044. \nonumber \]

    意义

    这个位置介于两个最小值之间，非常接近最大值的位置、预期接近\(\beta = 3\pi/2\)或的位置\(1.5\pi\)。

    练习\(\PageIndex{1}\)

    对于示例中的实验\(\PageIndex{1}\)，从中心到哪个角度是第三个最大值，相对于中心最大值，它的强度是多少？

    回答

    \(74.3^o\)，\(0.0083 I_0\)

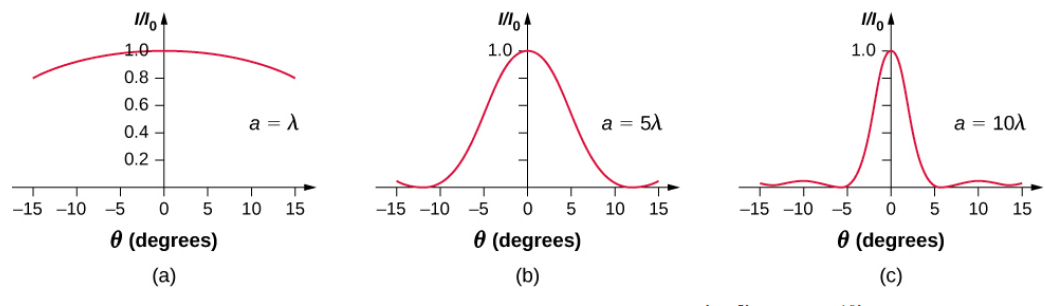
    如果狭缝宽度变化，\(a\)则强度分布会发生变化，如图所示\(\PageIndex{4}\)。 中心峰分布在从\(sin \, \theta = -\lambda/a\)到的区域内\(sin \, \theta = +\lambda/a\)。 对于小 β，这相当于角宽度\(\Delta \theta \approx 2\lambda /a\)。 因此，狭缝宽度的增加会导致中心峰宽度的减小。 对于带有 ≫ λ的狭缝，中心峰非常尖锐，而如果是 β l，则会变得相当宽。

    图 a 到 c 显示了 I 乘 I0 和 theta 的图表（以度为单位）。 每个波峰都有一个波峰，在 x=0 处的 y 值为 1。 标有 lambda 等于 lambda 的图 a 的弧线很宽。 标有 a 等于 5 lambda 的图 b 的波峰较窄。 它的零大致介于 10 和 15 之间，在负 10 和负 15 之间。 标为 a 等于 10 lambda 的图 c 有一个狭窄的波峰。 它在正负 5 处有零，大致介于 10 和 15 之间，在负 10 和负 15 之间。
    图\(\PageIndex{4}\)：不同狭缝宽度的单缝衍射图案。 当狭缝宽度 a 从 a =l 增加到 5λ然后增加到 10λ时，中心峰的宽度会随着第一个最小值的角度减小而减小，如方程 4.2.1 所预测。
    衍射模拟

    光学中的衍射实验可能需要大量的准备，但是安德鲁·达菲的模拟不仅可以快速设置，而且还能够立即改变狭缝宽度。 运行仿真并选择 “单狭缝”。 您可以调整狭缝宽度，并在屏幕上和图表中查看对衍射图案的影响。