4.2: 单缝衍射

Last updated
Save as PDF

Page ID: 201997

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释衍射现象及其观察条件
描述通过单个狭缝进行的衍射

在穿过狭窄的孔径（开口）后，向特定方向传播的波浪往往会扩散。例如，即使听者位于房间的一部分，光线传播的几何形状规定只能保持沉默，也可以听到通过敞开的门进入房间的声波。同样，穿过防波堤开口的海浪可以蔓延到里面的整个海湾。（图\(\PageIndex{1}\)）。声音和海浪的传播和弯曲是衍射的两个例子，衍射是波浪在开口或障碍物的边缘弯曲，所有类型的波浪都表现出这种现象。

照片显示了海滩附近防波堤的俯视图。防波堤上有一个开口，可以让海浪进入。 — 图\(\PageIndex{1}\)：由于海浪的衍射，通过防波堤开口进入的海浪可以蔓延到整个海湾。（来源：修改谷歌地球的地图数据）

声波的衍射对我们来说是显而易见的，因为可听区域中的波长与它们遇到的物体的大小大致相同，要想轻松观察到衍射效应，就必须满足这一条件。由于可见光的波长范围约为 390 到 770 nm，因此大多数物体不会显著衍射光。但是，确实会出现孔径足够小以至于可以观察到光的衍射的情况。例如，如果你将中指和食指靠在一起，透过开口看一个灯泡，你会看到一个相当清晰的衍射图案，由平行于手指的明线和暗线组成。

通过单缝衍射

穿过单个狭缝的光所形成的衍射图案与我们在干涉一章中讨论的双狭缝或衍射光栅形成的衍射图案略有不同。 \(\PageIndex{2}\)该图显示了单缝衍射图案。请注意，两侧的中心最大值都大于最大值，并且两侧的强度都会迅速降低。相比之下，衍射光栅会产生间隔均匀的线条，在中心两侧缓慢变暗。

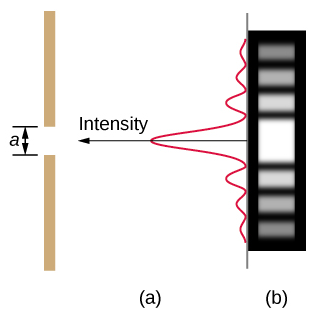
图 a 显示了左侧的一条垂直线。它的间隙长度为 a。右侧显示的是垂直波浪。波浪的中心有一个高峰，对应于狭缝。波浪在顶部和底部都会衰减。沿着波浪中央波峰指向狭缝的箭头被标记为强度。图 b 显示了带有水平标记的浅线和暗线的条带。与缝隙相对应的中心线是最亮的。 — 图\(\PageIndex{2}\)：单缝衍射图案。 (a) 穿过单个狭缝的单色光具有中心最大值，两侧都有许多更小且更暗的最大值。中心最大值比显示的要高六倍。 (b) 该图显示了亮度中心最大值，两侧显示了较暗和较薄的最大值。

单缝衍射的分析如图所示\(\PageIndex{2}\)。在这里，光线到达狭缝，均匀照亮它，并在其宽度上同相。然后，我们考虑光从同一狭缝的不同部分向前传播。根据惠更斯的原理，狭缝中波锋的每个部分都会发射小波，正如我们在《光的本质》中所讨论的那样。这些光线就像是从相位开始向四面八方传播的光线。（每条射线都垂直于小波的波锋。）假设屏幕与缝隙的大小相比非常远，那么朝向共同目的地的光线几乎是平行的。当它们直行时，如图（a）部分所示，它们保持同相，我们观察到中心最大值。但是，当光线相对于光束的原始方向以一定角度 β 传播时，每条射线移动到公共位置的距离不同，它们可以相位或异相。在 (b) 部分中，来自底部的射线比来自顶部的射线传播距离一个波长 λ的距离。因此，来自中心的射线比狭缝底部边缘的射线传播距离小 λ/2，异相并产生破坏性干扰。从稍高于中心的一条射线和一条来自稍高于底部的射线也会相互抵消。实际上，来自狭缝的每条射线都会破坏性地干扰另一条射线。换句话说，成对消除所有光线会使该角度下的强度达到暗的最小值。通过对称性，另一个最小值出现在光的入射方向右侧（朝向图底部）的相同角度。

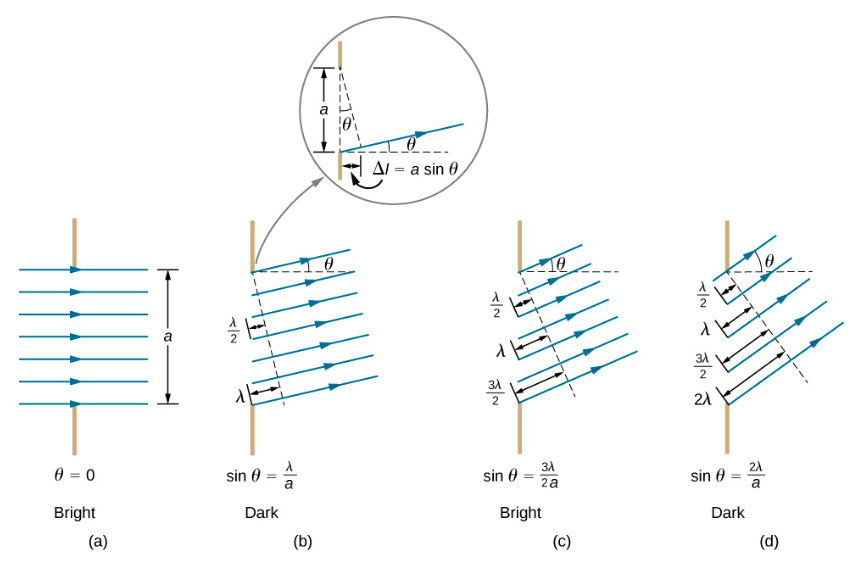
图 a 显示水平光线从左向右穿过长度为 a 的垂直狭缝。这被标记为 theta 等于零，明亮。图 b 显示光线以 theta 与水平方向成一定角度穿过狭缝。它被标记为 sine theta 等于 lambda 乘以 a，dark。一条垂直于光线的虚线触及狭缝的顶部。它与狭缝底部的垂直距离为 lambda，距离狭缝中心的垂直距离为 lambda x 2。另一个视图显示虚线与垂直方向成一定角度 theta。它在特定点与从狭缝底部开始的射线相交。该点与狭缝的水平距离为 delta l，等于正弦西塔。图 c 显示光线以 theta 与水平成一定角度穿过狭缝。它被标记为 sine theta 等于 3 lambda x 2 a，亮。一条垂直于光线的虚线触及狭缝的顶部。它与狭缝底部的垂直距离为 3 lambda x 2。图 d 显示光线以 theta 与水平方向成一定角度穿过狭缝。它被标记为 sine theta 等于 2 lambda 乘以 a，dark。一条垂直于光线的虚线触及狭缝的顶部。它与狭缝底部的垂直距离为 2 lambda。 — 图\(\PageIndex{3}\)：穿过单个狭缝的光会向各个方向衍射，并可能产生建设性或破坏性干扰，具体取决于角度。来自狭缝两侧的射线的路径长度差异可以看作是\(\sin θ\).

在 (c) 部分所示的较大角度下，来自狭缝顶部和底部的光线的路径长度会有所不同。\(3λ/2\) 一条射线从底部传播的距离\(λ\)与射线的距离不同，相位到达，具有建设性的干扰。两条光线，每条光线都略高于这两条射线，也具有建设性的作用。来自狭缝的大多数射线都有另一条光线需要建设性地干扰，并且在这个角度下会出现最大强度。但是，并非所有射线都会对这种情况产生建设性的干扰，因此最大值不如中心最大值那么强烈。最后，在 (d) 部分中，显示的角度足够大，足以产生第二个最小值。如图所示，来自狭缝两侧的射线的路径长度差异为\(a \sin \theta\)，并且我们可以看到，当该距离是波长的整数倍时，可以获得破坏性最小值。

因此，要获得对单个缝隙的破坏性干扰，

\[\underbrace{a \sin θ = mλ}_{\text{destructive interference}} \nonumber \]

哪里

\(m = ±1, ±2, ±3,...\)，
\(a\)是缝隙宽度，
\(λ\)是光的波长
\(θ\)是相对于光源原始方向的角度，并且
\(m\)是最小值的顺序。

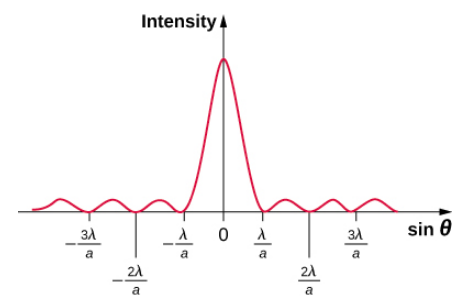
该图\(\PageIndex{3}\)显示了单缝干扰的强度图，很明显，中心最大值两侧的最大值强度要小得多，也没有那么宽。在双缝衍射中探讨了这种效果。

该图显示了强度与正弦西太差的对比图。正弦太等于 0 时，强度为最大值。两边都有较小的波峰，正弦波峰等于负 2 lambda a，减去 lambda a、lambda a、2 lambda a，依此类推。 — 图\(\PageIndex{3}\)：一张单缝衍射强度图，显示中心最大值比侧面的最大值更宽，强度更大。实际上，中心最大值比此处显示的要高六倍。

示例\(\PageIndex{1}\): Calculating Single-Slit Diffraction

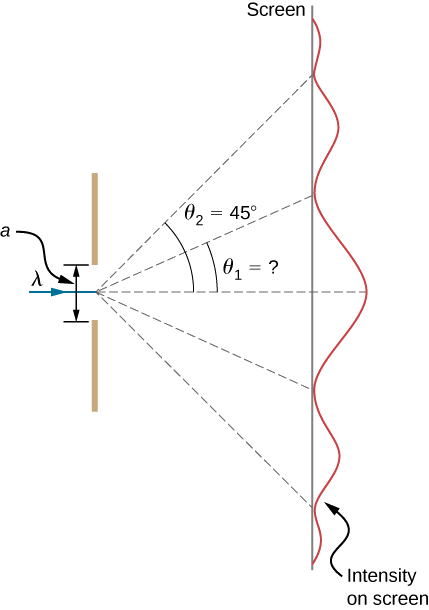
波长为 550 nm 的可见光落在单个狭缝上，相对于光的入射方向以 45.0° 的角度产生最小第二次衍射，如图所示\(\PageIndex{5}\)。

缝隙的宽度是多少？
第一个最小值是在什么角度产生的？

该图显示了左侧的一条垂直线。中间有一条长度为 a 的狭缝。一条标有 lambda 的射线水平穿过狭缝。这会分成5条落在屏幕上的虚线。屏幕显示为一条垂直线。在五条虚线中，有两条与水平线形成角度 theta 1 和 theta 2。西塔 2 是 45 度。 Theta 1 小于 theta 2 且未知。屏幕上的强度显示为垂直波浪。中间的波峰是最大的，从缝隙中心开始的水平虚线落在屏幕上。波浪在顶部和底部衰减。剩下的四条虚线对应于波浪中的低谷。 — 图\(\PageIndex{5}\)：在本例中，我们分析了单缝衍射图案的图形。

策略

根据给定的信息，假设屏幕离狭缝很远，我们可以先使用方程来找\(a\)出\(a \sin θ = mλ\)第一个最小值的角度\(\theta_1\)。

解决方案

我们得到了\(λ=550\,nm\)\(m=2\)、和\(\theta_2 = 45.0°\)。求解方程\(a\)并\(a \, \sin \, \theta = m\lambda\)用已知值代替得出
\[a = \frac{m\lambda}{\sin \, \theta_2} = \frac{2(550 \, nm)}{\sin \, 45.0°} = \frac{1100 \times 10^{-9} m}{0.707} = 1.56 \times 10^{-6} m. \nonumber \]
求解方程\(\sin \, \theta_1\)并\(a \, \sin \, \theta = m\lambda\)用已知值代替得出
\[\sin \, \theta_1 = \frac{m\lambda}{a} = \frac{1(550 \times 10^{-9}m)}{1.56 \times 10^{-6}m}. \nonumber \]
因此，角度\(\theta_1\)为
\[\theta_1 = \sin^{-1}0.354 = 20.7°. \nonumber \]

意义

我们看到狭缝很窄（它只比光的波长大几倍）。这与以下事实一致：光必须与大小与其波长相当的物体相互作用，才能表现出明显的波浪效应，例如这种单缝衍射图案。我们还看到，中心最大值在原始光束的两侧延伸了 20.7°，宽度约为 41°。第一个和第二个最小值之间的角度仅为 24° (45.0°−20.7°)。因此，第二个最大值的宽度仅为中心最大值的一半左右。

练习\(\PageIndex{1}\)

假设示例中的狭缝宽\(\PageIndex{1}\)度增加到\(1.8 \times 10^{-6} m\)。第一个、第二个和第三个最小值的新角度位置是什么？第四个最低限度会存在吗？

回答: \(17.8^o\),\(37.7^o\),\(66.4^o\); 没有