3.E：干扰（练习）

概念性问题

3.1 Young 的双缝干扰

1。 杨的双缝实验将单个光束分解成两个光源。 两个独立的光源，例如遥远汽车的大灯，能否获得相同的图案？ 解释一下。

2。 是否有可能创建一个只有破坏性干扰的实验装置？ 解释一下。

3。 为什么两个紧密相连的小钠灯不会在遥远的屏幕上产生干扰图案？ 如果用两个紧密相连的激光笔代替钠灯会怎样？

3.2 干扰数学

4。 假设你使用同样的双缝在空中进行 Young 的双缝实验，然后在水中重复这个实验。 与干涉图案相同部分的角度会变大还是变小？ 灯光的颜色会改变吗？ 解释一下。

5。 为什么在双缝实验中使用单色光？ 如果使用白光会发生什么？

3.4 薄膜中的干扰

6。 增加楔角会对干涉条纹的间距产生什么影响？ 如果楔角过大，则不会观察到条纹。 为什么？

7。 两个原本同相的光波所走路径的差异与它们是建设性干扰还是破坏性干扰有何关系？ 这怎么会受到反射的影响？ 通过折射？

8。 漂浮在人泪层上的隐形眼镜任一表面反射的光线是否有相位变化？ 镜头的折射率约为1.5，其顶部表面干燥。

9。 将样品放在显微镜载玻片上时，在玻璃载玻片上的水滴上放置一个玻璃盖。 从上方入射的光线可以从玻璃盖的顶部和底部以及水滴下方的玻璃滑梯反射。 在哪些表面，反射光会发生相位变化？

10。 如果两块皇冠玻璃之间的液体是二硫化碳，请回答上述问题。

11。 在考虑一片火腿的食物价值时，你会注意到它潮湿的表面反射出彩虹般的颜色。 解释其起源。

12。 一位发明家注意到肥皂泡最薄时是深色的，并意识到所有波长都在发生破坏性干扰。 她怎么能利用这些知识为镜头制造一种在所有波长下都有效的非反射涂层？ 也就是说，涂层的折射率和厚度会有什么限制？ 这怎么可能不切实际？

13。 像示例 3.3 中描述的那样的非反射涂层非常适合单波长和垂直入射。 其他波长和其他入射方向会发生什么？ 具体一点。

14。 为什么看见一块厚玻璃反射的光的干涉条纹比从薄膜上反射的光要难得多？ 如果使用单色光会更容易吗？

3.5 迈克尔逊干涉仪

15。 描述如何使用迈克尔逊干涉仪测量气体（包括空气）的折射率。

问题

3.2 干扰数学

16。 450 nm 波长的蓝光落在相隔 0.0500 mm 的双狭缝上，一阶最大角度是多少？

17。 计算落在相隔 0.100 mm 的双狭缝上的三阶最大波长为 580nm 的黄光的角度。

18。 610 nm 橙光的第一个最大角度为 610 nm 的两个狭缝之间的间隔是\(\displaystyle 30.0°\)多少？

19。 找出两个狭缝之间的距离，这两条缝隙在角度为 410 nm 紫光时产生第一个最小值\(\displaystyle 45.0°\)。

20。 计算落在分隔的双狭缝上\(\displaystyle 30.0°\)时其最小值为第三个最小的光的波长\(\displaystyle 3.00μm\)。 明确说明如何按照本章末尾的 “问题解决策略：Wave Optics” 中的步骤进行操作。

21。 \(\displaystyle 2.00μm\)如果三阶最大值的角度为，则落在双狭缝上的光的波长是\(\displaystyle 60.0°\)多少？

22。 在前述问题中，四阶最大值在哪个角度？

23。 落在被分隔的双缝上的 400 nm 光的最高阶数是\(\displaystyle 25.0μm\)多少？

24。 找出落在双狭缝上的最大光波长，两条狭缝之间有一阶最大值。\(\displaystyle 1.20μm\) 这是在光谱的可见部分吗？

25。 两个狭缝之间的最小间隔是多少，这将产生720纳米红光的二阶最大值？

26。 (a) 在任何可见光下产生二阶最大值的两个狭缝之间的最小间隔是多少？

(b) 适用于所有可见光？

27。 (a) 如果落在双缝上的单色光的一阶最大角度为\(\displaystyle 10.0°\)，则二阶最大角度是多少？

(b) 第一个最小值的角度是多少？

(c) 这里可能的最高阶数是多少？

28。 下图是一个距离屏幕 x 的双缝隙，距屏幕中心的距离由 y 给出。当缝隙之间的距离 d 相对较大时，会出现许多亮点，称为条纹。 表明，对于小角度（其\(\displaystyle θ\)中\(\displaystyle sinθ≈θ\)，以弧度为单位），条纹之间的距离由下式给出\(\displaystyle Δy=xλ/d\)

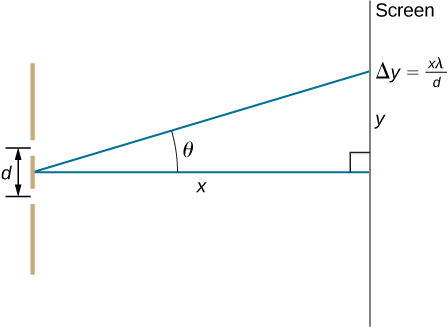
图中显示了一个距离屏幕 x 的双缝隙，距屏幕中心的距离由 y 给出。缝隙之间的距离为 d。

29。 根据前面问题的结果，

(a) 计算落在距离屏幕 3.00 m 的双狭缝上的 633 纳米光的条纹之间的距离，间隔为 0.0800 mm。

(b) 如果整个设备都浸入水中，折射率为1.33，则边缘之间的距离是多少？

30。 根据之前两个问题的结果，找出在屏幕上产生距离 0.120 mm 的双狭缝 2.00 m 的条纹的光的波长。

31。 在双缝实验中，在距离缝隙 1.5 米的屏幕上，第五个最大值距离中心最大值 2.8 cm。 如果狭缝相距 0.15 mm，则所用光的波长是多少？

32。 杨氏实验中的光源以两个波长发射。 在观察屏幕上，一个波长的第四个最大值与另一个波长的第五个最大值位于同一位置。 两个波长的比率是多少？

33。 如果500-nm和650nm的光照亮了两个相隔0.50毫米的狭缝，那么在2.0米外的屏幕上，这两个波长的二阶最大值相隔多远？

34。 波长为 700 nm 的红光落在由 400 nm 隔开的双缝上。

(a) 衍射图案中的一阶最大值在什么角度？

(b) 这个结果有什么不合理之处？

(c) 哪些假设不合理或不一致？

3.3 多缝干扰

35。 十个狭窄的狭缝间隔相等 0.25 mm，用波长为 580 nm 的黄光照亮。 (a) 第三和第四个主最大值的角度位置是多少？ (b) 屏幕上这些最大值与狭缝 2.0 米的距离是多少？

36。 明亮条纹的宽度可以计算为两侧两个相邻的深色条纹之间的间隔。 找出前面问题中三阶和四阶明亮条纹的角宽度。

37。 对于三缝干涉图案，求出次级最大值的峰值强度与主最大值的比率。

38。 干涉图案的中心条纹的角宽度是多少

(a) 20 个缝隙由\(\displaystyle d=2.0×10^{−3}mm\)？

(b) 50 个间距相同的狭缝？ 假设一下\(\displaystyle λ=600nm\)。

3.4 薄膜中的干扰

39。 肥皂泡的厚度为 100 nm，由垂直于其表面入射的白光照亮。 假设折射率与水相同，哪种波长和颜色的可见光最能建设性地反射？

40。 水面上的浮油厚度为 120 nm，由垂直于其表面入射的白光照亮。 鉴于其折射率为1.40，油会出现什么颜色（最具建设性的反射波长是多少）？

41。 计算浮油在被垂直于其表面的白光照亮时显示为蓝色的水上的最小厚度。 将蓝色波长设为 470 nm，将油的折射率设为 1.40。

42。 找出在垂直于其表面的白光照亮时显示为红色的肥皂泡的最小厚度。 将波长设为 680 nm，并假设折射率与水相同。

43。 塑料砧板顶部的肥皂水 (\(\displaystyle n=1.33\)) 薄膜厚度为 233 nm。 如果垂直于其表面照明，哪种颜色的反射效果最强？

44。 如果 Plexiglas 上肥皂水 (\(\displaystyle n=1.33\)) 在白光垂直照射时呈绿色（建设性地反射 520 纳米光），则其厚度最小的三种非零厚度是多少？

45。 假设你有一个主要用于 700 nm 红光的镜头系统。 在这个波长下不会反射的第二薄萤石（氟化镁）涂层是什么？

46。 (a) 当肥皂泡变薄时，它会变暗，因为与光的波长相比，路径长度的差异变小，并且顶部表面有相移。 如果路径长度差值小于波长的四分之一时变暗，那么在所有可见波长下，气泡的最大厚度是多少？ 假设折射率与水相同。

(b) 考虑到所发现的厚度，讨论薄膜的脆弱性。

47。 为了省钱让雷达看不见军用飞机，一位发明家决定在雷达上涂上折射率为1.20的非反射材料，该材料介于空气和飞机表面的折射率之间。 他认为，这应该比设计隐形轰炸机便宜得多。

(a) 涂层厚度应为多大才能抑制 4.00 厘米波长雷达的反射？

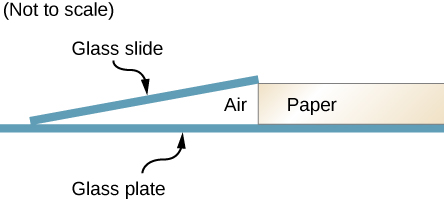
(b) 这个结果有什么不合理之处？

(c) 哪些假设不合理或不一致？

3.5 迈克尔逊干涉仪

48。 迈克尔逊干涉仪有两个相等的臂。 干涉仪使用波长为546 nm的汞光，并发现了稳定的条纹。 其中一只手臂被移动\(\displaystyle 1.5μm\)。 有多少边缘会穿过观测场？

49。 迈克尔逊干涉仪的行进镜移动的距离是多少，该干涉仪对应于经过观察屏幕某一点的 1500 条条纹？ 假设干涉仪是用 606 nm 的 krypton-86 光谱线照亮的。

50。 当迈克尔逊干涉仪的行进镜移动时\(\displaystyle 2.40×10^{−5}m\)，90 个条纹会经过观察屏幕上的一个点。 所用光的波长是多少？

51。 在迈克尔逊干涉仪中，使用来自氦铌激光器的波长为632.8 nm的光。 当其中一个镜像移动 D 的距离时，8 个条纹会移过视场。 距离 D 的值是多少？

52。 迈克尔逊干涉仪的一根臂上放置了一个长5.0厘米的腔室，两端有平行窗户（见下文）。 所用光在真空中的波长为 500 nm。 当所有空气都被抽出腔室时，有29个边缘经过观察屏幕上的一个点。 空气的折射率是多少？

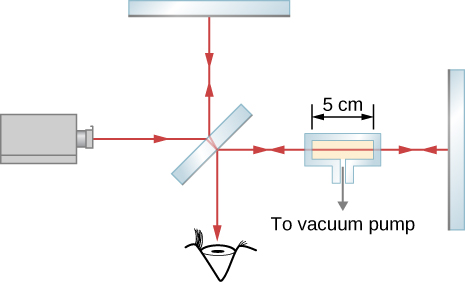
图为用于测量气体折射率的装置示意图。 装有气体的玻璃室放置在迈克尔逊干涉仪中，位于半镀银镜 M 和反射镜 M1 之间。 容器内部的空间宽度为 5 厘米。

其他问题

53。 对于 600 纳米波长的光和 0.12 mm 的狭缝间隔，双缝干涉图案中第一个和第三个最大值的角度位置是多少？

54。 如果前面问题中的光源发生变化，则发现第三个最大值的角度位置为\(\displaystyle 0.57°\)。 现在使用的光的波长是多少？

55。 红灯 (\(\displaystyle λ=710.nm\)) 照亮相隔一定距离的双缝隙\(\displaystyle d=0.150mm\)。 屏幕和缝隙相距 3.00 米。

(a) 在屏幕上找到中心最大值和第三个最大值之间的距离。

(b) 第二个和第四个最大值之间的距离是多少？

56。 两个源同相，用它发射波浪\(\displaystyle λ=0.42m\)。 确定在与两个来源距离较远的点发生的是建设性干扰还是破坏性干扰

(a) 0.84 和 0.42 m，

(b) 0.21 和 0.42 m，

(c) 1.26 和 0.42 m，

(d) 1.87 和 1.45 米，

(e) 0.63 和 0.84 m 以及

(f) 1.47 和 1.26 m。

57。 \(\displaystyle 4.0×10^{−6}m\)相隔的两个狭缝由波长为 600 nm 的光照亮。 干涉图案中的最高阶条纹是多少？

58。 假设可以观测到的最高阶条纹是使用 550 纳米波长光的双缝实验中的第八条条纹。 缝隙的最小间隔是多少？

59。 He-Ne 激光 (\(\displaystyle λ=632.9nm\)) 穿过相距 0.031 mm 的两个狭缝的干涉图案投射在 10.0 米外的屏幕上。 确定相邻明亮条纹之间的距离。

60。 Young 的双缝实验是在水中进行的 (\(\displaystyle n=1.333\))。 光源是真空\(\displaystyle λ=632.9nm\)中的 He-Ne 激光器。

(a) 这种光在水中的波长是多少？

(b) 两个间隔0.100 mm的狭缝的三阶最大角度是多少。

61。 将进行双缝实验，以便在距离两个缝隙2.13米的屏幕上出现相距1.27厘米的明亮条纹。 光源的波长为 500 nm。 两个缝隙之间的间隔应该是多少？

62。 声波会产生类似于双缝干扰的效果，而不是光线。 在空地上，两个相距 1.30 m 的扬声器由单功能发生器提供动力，以 1200 Hz 的频率产生正弦波。 学生沿着 12.5 米外的一条线行走，该线与扬声器之间的线平行。 由于建设性和破坏性的干扰，她听到大声和安静的交替模式。 （a）这个声音的波长是多少，（b）沿着这条线的中心最大值和第一个最大值（响亮）位置之间的距离是多少？

63。 氢气放电灯以四个波长（\(\displaystyle λ=\)410、434、486 和 656 nm）发射可见光。 (a) 如果这盏灯发出的光线落在相隔 0.025 mm 的 N 个缝隙上，那么在距离狭缝 2.0 米的屏幕上观看时，第三个最大值距离中心最大值有多远？ (b) 第二个和第三个最大值之间的距离是\(\displaystyle l=486nm\)多少？

64。 频率的单色光\(\displaystyle 5.5×10^{14}Hz\)落在相隔 0.020 mm 的 10 个狭缝上。 在距离狭缝 2.0 米的屏幕上，第一个和第三个最大值之间的间隔是多少？

65。 八个相等 0.149 mm 的狭缝由单色光均匀照亮\(\displaystyle λ=523nm\)。 在 2.35 米外的屏幕上，中心主角的最大宽度是多少？

66。 八个相等 0.149 mm 的狭缝由单色光均匀照亮\(\displaystyle λ=523nm\)。 与主最大值相比，次要最大值的强度是多少？

67。 厚度为 250 nm、折射率为 1.40 的透明薄膜被空气包围。 在近乎正常入射到胶片的白光束中，哪个波长在反射时会受到破坏性干扰？

68。 对于通过空气中的透明薄膜 (\(\displaystyle n=1.20\)) 传输的 450 nm 光，可以找到最小强度。

(a) 薄膜的最小厚度是多少？

(b) 如果该波长是出现强度最小值的最长波长，那么接下来的三个较低值会发生这种情况？\(\displaystyle λ\)

69。 一层薄薄的\(\displaystyle n=1.32\)薄膜被空气包围。 为了最大限度地减少正常入射光的反射，这种薄膜的最小厚度\(\displaystyle λ=500nm\)是多少？

70。 在平板玻璃 (\(\displaystyle n=1.50\)) 表面上放置薄膜，重复上一个问题的计算。

71。 在一次轻微的漏油事件之后，一层厚度为 450 nm 的 think oil (\(\displaystyle n=1.40\)) 薄膜漂浮在海湾的水面上。 (a) 飞过头顶的鸟能看到什么主要颜色？ (b) 海豹在水下游泳时会看到什么主要颜色？

72。 一张10厘米长的显微镜载玻片与一端的玻璃板之间用一张纸隔开。 如下所示，幻灯片的另一端与板材接触。由钠灯发出的光线从上方照亮幻灯片 (\(\displaystyle λ=589nm\))，沿着幻灯片可以看到每厘米有 14 个条纹。 这张纸的厚度是多少？ 图为一张显微镜载玻片，它在一端接触玻璃板，另一端被一张纸隔开。

73。 假设上述问题的设置浸入未知液体中。 如果现在在幻灯片上看到每厘米有 18 个条纹，那么液体的折射率是多少？

74。 当将两块平板玻璃板放在彼此之上并在它们之间的一边插入一张纸条时，就会产生一个充满空气的薄楔子。 当在反射中看到垂直落在板上的单色光时，就会观察到干涉条纹。 靠近板块接触边缘的第一个边缘是明亮的边缘还是深色边缘？ 解释一下。

75。 使用两块相同的矩形平板玻璃来测量头发的厚度。 玻璃板在一个边缘直接接触，在它们之间放一根头发，听到另一边的声音。 用钠灯 (\(\displaystyle λ=589nm\)) 照亮时，可以看到头发介于第 180 和第 181 个深色边缘之间。 头发直径的下限和上限是多少？

76。 两张由玻璃制成的显微镜载玻片由垂直入射的单色 (\(\displaystyle λ=589nm\)) 光照亮。 顶部幻灯片一端接触底部幻灯片，另一端靠在一根细铜线上，形成空气楔子。 铜线的直径为 29.45 微米。 在这些幻灯片上可以看到多少明亮的条纹？

77。 质量好的相机 “镜头” 实际上是一个镜头系统，而不是单镜头，但副作用是来自一个镜头表面的反射可以在系统内反射多次，从而在照片中产生伪影。 为了解决这个问题，这种系统中的一个镜头在一侧涂有一层薄薄的材料（\(\displaystyle n=1.28\)）。 镜头玻璃的折射率为 1.68。 通过破坏性干扰减少640 nm处反射的最小涂层厚度是多少？ （换句话说，涂层的效果需要优化\(\displaystyle λ=640nm\)。）

78。 从浮油正上方观察到波长（空中）440 nm 和 616 nm 的构造干扰。 这种油的折射率是\(\displaystyle n=1.54\)。 薄膜可能的最小厚度是多少？

79。 肥皂泡被吹到室外。 反射阳光的哪些颜色（用波长表示）得到了增强？ 肥皂泡的折射率为 1.36，厚度为 380 nm。

80。 带有 He-Ne 激光光源 (\(\displaystyle λ=632.8nm\)) 的迈克尔逊干涉仪将其干扰图案投射到屏幕上。 如果导致可移动的镜子移动\(\displaystyle 8.54μm\)，则会观察到多少条纹通过屏幕上的参考点移动？

81。 当迈克尔逊干涉仪中的可移动反射镜移位时，实验人员检测到 251 个条纹。 使用的光源是钠灯，波长为 589 nm。 可移动的镜子移动了多远的距离？

82。 迈克尔逊干涉仪用于测量穿过它的光的波长。 当可移动镜子正好移动 0.100 mm 时，观察到的穿过的条纹数量为 316。 光的波长是多少？

83。 使用 633 纳米光源将一个 5.08 厘米长的矩形玻璃腔插入迈克尔逊干涉仪的一根臂中。 该腔室最初在标准大气压下充满空气 (\(\displaystyle n=1.000293\))，但空气会使用真空泵逐渐抽出，直到达到接近完美的真空。 在过渡期间，观察到有多少条条纹在移动？

84。 在迈克尔逊干涉仪的一根臂上插入一块厚\(\displaystyle 75μm\)度的塑料片，这会导致干涉图案偏移86个条纹。 光源在空气中的波长为 610 nm。 这种塑料的折射率是多少？

85。 铝箔的厚度是使用迈克尔逊干涉仪测量的，该干涉仪的移动镜安装在千分尺上。 当千分尺夹在箔片上时，观察到的干扰图案与千分尺空时观察到的干扰图案有27个条纹的差异。 计算铝箔的厚度？

86。 迈克尔逊干涉仪的可移动镜安装在长度为 23.3 mm 的细金属棒的一端。 杆的另一端是固定的，因此它不会移动。 当棒的温度从变\(\displaystyle 15°C\)为\(\displaystyle 25C\)时，观察到了 14 个条纹的变化。 光源是 He Ne 激光，\(\displaystyle λ=632.8nm\)。 金属棒的长度变化是多少，它的热膨胀系数是多少？

87。 在热稳定实验室中，迈克尔逊干涉仪用于监测温度，以确保温度保持恒定。 可移动的镜子安装在一根1.00米长的铝棒的末端，固定在另一端。 光源是 He Ne 激光，\(\displaystyle λ=632.8nm\)。 该设备的分辨率对应于仅观察到一条条纹变化时的温差。 这个温差是多少？

88。 当一只手臂上放置由未知材料制成的\(\displaystyle 42.0-μm\)胶片时，65 条纹偏移会产生迈克尔逊干涉仪。 光源的波长为 632.9 nm。 使用表 1.1 中的折射指数识别材质。

挑战问题

89。 确定如果其中一个缝隙被厚度为 λ/ [2 (n−1)] λ/ [2 (n−1)] 的薄透明薄膜覆盖，其中 λλ是入射光的波长，n 是薄膜的折射率，则双缝干涉图案会发生什么。

90。 五十一条狭缝间隔相等，间隔为 0.10 mm。 狭缝由波长为 400 nm 的蓝光照亮。 第 25 个次要最大值的角度位置是多少？ 与初级最大值相比，它的峰值强度是多少？

91。 水上的油膜在很薄时会显得很暗，因为与光的波长相比，路径长度的差异很小，并且顶部表面会有相移。 如果路径长度差小于波长的四分之一时变暗，那么在所有可见波长下，油的最厚是多少？ 石油的折射率为 1.40。

92。 图 3.14 显示了由垂直入射的单色光照亮的两张玻璃幻灯片。 顶部幻灯片一端接触底部幻灯片，另一端停留在直径为0.100毫米的头发上，形成一团空气。 (a) 如果幻灯片长 7.50 厘米且使用 589 纳米光，则暗带之间的距离有多远？ (b) 如果幻灯片是用皇冠玻璃还是火石玻璃制成，有什么区别吗？ 解释一下。

93。 图 3.14 显示了两张 7.50 厘米长的玻璃幻灯片，由垂直入射的纯 589 nm 波长光照亮。 顶部幻灯片一端接触底部幻灯片，另一端停留在一些碎片上，形成空气楔形。 如果暗带相距 1.00 毫米，碎片有多厚？

94。 肥皂泡的厚度为 100 nm，由与其表面成\(\displaystyle 45°\)一定角度入射的白光照亮。 假设折射率与水相同，哪种波长和颜色的可见光最能建设性地反射？

95。 水面上的浮油厚度为 120 nm，由与其表面成\(\displaystyle 45°\)一定角度入射的白光照亮。 鉴于其折射率为1.40，油会出现什么颜色（最具建设性的反射波长是多少）？