3.6: 迈克尔逊干涉仪

Last updated
Save as PDF

Page ID: 202438

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释使用迈克尔逊干涉仪观察到的由镜面运动引起的条纹变化
解释使用迈克尔逊干涉仪观察到的由介质变化引起的条纹变化

迈克尔逊干涉仪（由美国物理学家阿尔伯特·迈克尔森发明，1852-1931 年）是一种精密仪器，它通过将光束分成两部分，然后在光束经过不同的光路后将其重组来产生干涉条纹。该图\(\PageIndex{1}\)描绘了干涉仪和来自扩展光源 S 上单点的光束路径，扩展光源 S 是一块磨砂玻璃板，用于扩散来自波长的单色灯的光\(\lambda_0\)。光束击中半银镜 M，其中一半反射到侧面，一半穿过镜子。反射的光传输到可移动的平面反射镜\(M_1\)，在那里它通过 M 反射回观察者。原始光束的透射一半由固定镜反射回去，\(M_2\)然后由 M 向观察者反射。

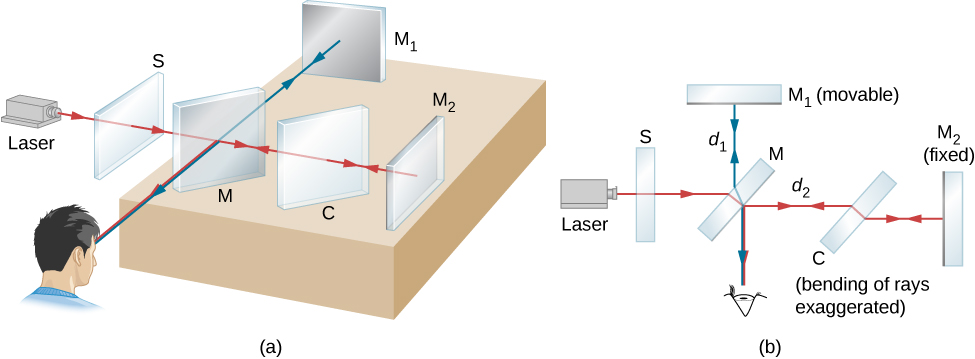
图 A 显示了迈克尔逊干涉仪的示意图。图 B 是迈克尔逊干涉仪的平面视图。激光发出的光束带着缝隙穿过屏幕 S。它击中了半银镜 M，其中一半反射到侧面，一半穿过镜子。反射光传输到可移动的平面反射镜 M1，然后通过 M 反射回观察者。原始光束的透射一半由固定镜 M2 反射回去，然后被 M 向观察者反射。 — 图\(\PageIndex{1}\)：(a) 迈克尔逊干涉仪。延伸光源是一块磨砂玻璃板，用于扩散激光发出的光。 (b) 干涉仪的平面视图。

由于两个光束都来自光源上的同一点，因此它们是相干的，因此会产生干扰。从图中可以看出，一个光束穿过 M 三次，另一个光束只穿过一次。为了确保两根光束穿过相同厚度的玻璃，在装有透明玻璃的补偿板 C 中放置了一块由透明玻璃制成的补偿板 C\(M_2\)。这块板是 M 的复制品（没有镀银），通常是用用于生产 M 的同一块玻璃切割而成的。补偿器安装到位后，两根光束之间的任何相位差都完全是由于它们行进距离的差异造成的。

两个光束重组时的路径差为\(2d_1 - 2d_2\)，其中\(d_1\)是 M 和 M 之间的距离\(M_1\)，\(d_2\)是 M 和 M 之间的距离\(M_2\)。假设此路径差异是一个整数波长\(m\lambda_0\)。然后，出现建设性干扰，在观察者身上可以看到光源上点的明亮图像。现在，如果两个光束的路径差异相同，则来自光源上任何其他点的光也会受到建设性的干扰并产生明亮的图像。这些点图像的集合是一个明亮的条纹，对应于路径差异为\(m\lambda_0\)（图\(\PageIndex{2}\)）。当\(M_1\)移动一段距离时\(\Delta d = \lambda_0/2\)，此路径差异会改变\(\lambda_0\)，并且每个条纹都会移动到先前被相邻条纹占据的位置。因此，通过计算移动时经过给定点的条纹数 m，观察者可以测量精确到波长一小部分的微小位移，如关系所示\(M_1\)

\[\Delta d = m\dfrac{\lambda_0}{2}. \nonumber \]

图为使用迈克尔逊干涉仪制作的条纹的照片。条纹可见为交替出现的黑眼圈和浅色圆圈。 — 图\(\PageIndex{2}\)：使用迈克尔逊干涉仪制作的条纹。（来源：“SillagesVideos” /YouTube）

示例\(\PageIndex{1}\): Precise Distance Measurements by Michelson Interferometer

迈克尔逊干涉仪使用波长为 630 nm 的红色激光。在保持镜子\(M_1\)固定的同时，镜子\(M_2\)会移动。在观众中，发现边缘会越过固定的十字线。找出镜\(M_2\)子移动到单条条纹越过参考线的距离。

策略

有关几何图形，\(\PageIndex{1}\)请参阅图。我们使用迈克尔逊干涉仪干扰条件的结果来找出移动的距离\(Δd\)。

解决方案

对于 630 nm 的红色激光和每个条纹交叉点 (\(m = 1\))，\(M_2\)如果你保持\(M_1\)固定，行驶的距离为

\[\Delta d = m\dfrac{\lambda_0}{2} = 1 \times \dfrac{630 \, nm}{2} = 315 \, nm = 0.315 \, \mu m.\nonumber \]

意义

这种测量的一个重要应用是定义标准仪表。正如《单位和测量》中所述，标准仪表的长度曾经被定义为迈克尔逊干涉仪中的镜面位移，对应于气体放电管中 krypton-86 特定条纹的 1,650,763.73 个波长。

测量气体的折射率

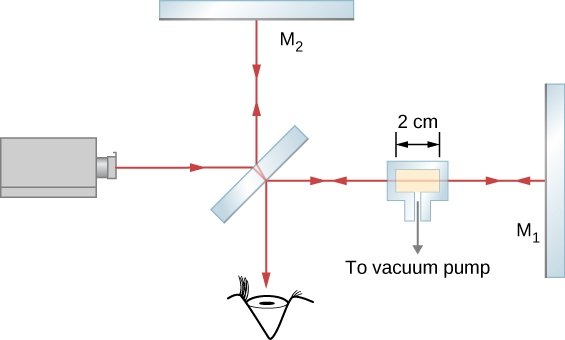
在迈克尔逊干涉仪的一个臂上，放置了一个玻璃室，里面装有用于排空内部并将气体放入其中的附件。容器内的空间宽 2 厘米。最初，容器是空的。当气体慢慢进入腔室时，你会观察到深色边缘会越过观测场中的参考线。当腔室被填充到所需的压力时，你已经计算出122个条纹越过了参考线。所用光的波长为 632.8 nm。这种气体的折射率是多少？

图片显示了用于测量气体折射率的装置示意图。装有气体的玻璃室放置在迈克尔逊干涉仪中，位于半镀银镜 M 和反射镜 M1 之间。容器内的空间宽 2 厘米。

策略

观察到的 m = 122 条纹构成了空腔室（真空）中适合的波长数量与充气时在同一腔室内适合的波长数量之间的差异。填充腔室中的波长缩短了 n 倍，即折射率。

解决方案

光线穿过玻璃室向右移动 t = 2 cm 的距离，在反射时向左移动另一距离 t。总行程为 L = 2t。空时，适合该腔室的波长数为

\[N_0 = \dfrac{L}{\lambda_0} = \dfrac{2t}{\lambda_0} \nonumber \]

其中\(\lambda_0 = 632.8\) nm 是所用光在真空中的波长。在任何其他介质中，波长为\(\lambda = \lambda_0/n\)，装在充气室中的波长数为

\[N = \dfrac{L}{\lambda} = \dfrac{2t}{\lambda_0/n}. \nonumber \]

过渡中观察到的条纹数为

\[\begin{align*} m = N - N_0, \\[4pt] &= \dfrac{2t}{\lambda_0/n} - \dfrac{2t}{\lambda_0}, \\[4pt] &= \dfrac{2t}{\lambda_0}(n - 1). \end{align*} \nonumber \]

求解 (n−1) 得出

\[n - 1 = m \left(\dfrac{\lambda_0}{2t}\right) = 122 \left(\dfrac{632.8 \times 10^{-9}m}{2(2 \times 10^{-2}m)}\right) = 0.0019 \nonumber \]

和\(n = 1.0019\)

意义

气体的折射指数非常接近真空的折射率，因此我们通常认为它们等于 1。 1 和 1.0019 之间的差异非常小，因此测量需要相应的灵敏技术，例如干涉测量。例如，我们不能指望使用仅基于斯内尔定律的技术来衡量这个值。

练习\(\PageIndex{1}\)

尽管观测到的条纹数 m 是一个整数，通常被认为不确定性为零，但实际上，在计算条纹时很容易忘记。在示例中\(\PageIndex{1}\)，如果你估计在报告条纹时可能错过了多达五个\(m=122\)条纹，(a) 示例中计算出的折射率值是\(\PageIndex{1}\)太大还是太小？ (b) 多少？

回答: a. 太小；b. 最多可达\(8 \times 10^{-5}\)

问题解决策略：波动光学

第 1 步。 检查情况以确定是否存在干扰。确定问题中是否考虑了狭缝、薄膜或干涉仪。
第 2 步。 如果涉及狭缝，请注意衍射光栅和双狭缝产生的干涉图案非常相似，但光栅的最大值更窄（更清晰）。单缝图案的特点是中心最大值较大，两侧最大值较小。
第 3 步。 如果涉及薄膜干扰或干涉仪，请注意干扰的两条射线之间的路径长度差。一定要使用所涉介质中的波长，因为它与真空中的波长不同。另请注意，当光线从折射率较高的介质反射时，会有额外的 λ/2λ/2 相移。
第 4 步。 准确确定问题中需要确定的内容（找出未知数）。书面清单很有用。绘制情况图。给图加标签很有用。
第 5 步。 如上所述，列出给出或可以从问题中推断出的内容（找出已知数）。
第 6 步。 求解要确定的量（未知）的相应方程并输入已知数。狭缝、光栅和瑞利极限涉及方程。
第 7 步。 对于薄膜干扰，总偏移具有构造干扰，即波长的整数。如果波长的总偏移量为半整数，则会产生破坏性干扰。永远记住，波峰到波峰是建设性的，而波峰到低谷是破坏性的。
第 8 步。 检查答案是否合理：有意义吗？ 例如，干涉图案中的角度不能大于 90°。