3.5: 薄膜中的干扰
- Page ID
- 202472
在本节结束时,您将能够:
- 描述反射时发生的相位变化
- 描述由常见光源的反射光线形成的条纹
- 解释薄膜中颜色的外观
漂浮在水上的浮油或阳光明媚的肥皂泡中看到的鲜艳色彩是由干扰引起的。 最亮的颜色是那些具有建设性干扰作用的颜色。 这种干涉发生在从薄膜的不同表面反射的光之间;因此,这种效应被称为薄膜干扰。
正如我们之前指出的那样,当光与大小与其波长相似的物体相互作用时,干扰效应最为明显。 薄膜是指厚度\(t\)小于光波长几倍的薄膜\(λ\)。 由于颜色与颜色间接相关,\(λ\)并且由于所有干扰在某种程度上都取决于所涉及物体大小的比例,因此我们应该期望看到不同厚度的薄膜会有不同的颜色,如图所示\(\PageIndex{1}\)。\(λ\)

什么原因导致薄膜干扰? 该图\(\PageIndex{2}\)显示了从胶片顶部和底部表面反射的光如何干扰。 入射光仅部分从胶片的顶部表面(射线 1)反射。 其余部分进入胶片,其本身从底部表面部分反射。 从底部表面反射的部分光线可能从胶片顶部冒出(射线 2),干扰从顶部反射的光(射线 1)。 进入胶片的光线传播的距离更长,因此它可能与从顶部反射的光线处于同相或异相。 但是,请再考虑一下图中的气泡\(\PageIndex{1}\)。 气泡在最薄的地方最暗。 此外,如果你仔细观察肥皂泡,你会注意到它在破裂时变暗了。 对于非常薄的薄膜,图中射线 1 和 2 的路径长度差异可以忽略\(\PageIndex{2}\)不计,那么为什么它们会产生破坏性干扰而不是建设性干扰呢? 答案是,反射时可能会发生相位变化,如下所述。
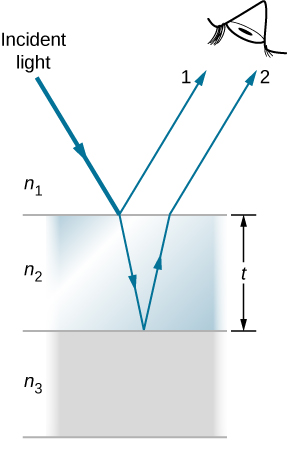
反射导致的相位变化
我们之前看到(Waves),机械波的反射可能涉及 180° 的相位变化。 例如,在较重的琴弦所连接的边界处反射时,弦上的行波会被反转(即 180° 的相位变化)。 但是,如果第二根弦更轻(或者更确切地说,线性密度较低),则不会发生反转。 光波产生相同的效果,但光的决定性参数是折射率。 光波在界面反\(\pi\)射时会发生180°或弧度的相位变化,超过该界面是折射率更高的介质。 从折射率较低的介质反射时不会发生相位变化(图\(\PageIndex{3}\))。 由于波浪的周期性质,这种相位变化或反转等\(±λ/2\)于行进距离或路径长度。 路径长度和折射率都是薄膜干扰的重要因素。
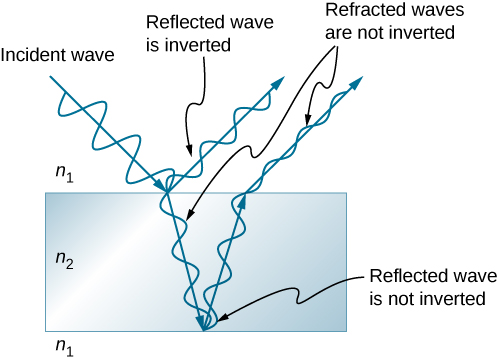
如果图中的胶片\(\PageIndex{3}\)是肥皂泡(本质上是两面都有空气的水),则射线 1\(λ/2\) 会出现相移,但射线 2 不会。 因此,当薄膜非常薄且两条光线之间的路径长度差异可以忽略不计时,它们完全不相位,并且在所有波长下都会发生破坏性干扰。 因此,这里的肥皂泡是黑暗的。 薄膜相对于光波长的厚度是薄膜干扰的另一个关键因素。 图中的射线 2 的\(\PageIndex{3}\)行进距离比射线 1 要长。 对于垂直于表面入射的光,射线 2 的传播距离大约比射线 1\(2t\) 远。 当该距离是介质中波长的整数倍或半整倍数时(其中 β 是真空中的波长\(\lambda_n = \lambda/n\),\(n\)是折射率),则会发生构造干扰或破坏性干扰,这也取决于任一射线中是否存在相位变化。
复杂的相机使用一系列多个镜头。 光线会从这些不同镜头的表面反射出来,从而降低图像的清晰度。 为了限制这些反射,镜片上涂了一层薄薄的氟化镁,这会造成破坏性的薄膜干扰。 如果它的折射率为1.38,并且设计用于限制550纳米光(通常是最强烈的可见波长)的反射,那么这部薄膜最薄的是多少? 假设玻璃的折射率为 1.52。
策略
参见图\(\PageIndex{2}\),\(n_1 = 1.00\)用于空气\(n_2 = 1.38\)、和\(n_3 = 1.52\)。 射线 1 和射线 2 在反射时都有 λ/2 的偏移。 因此,为了获得破坏性干扰,射线 2 需要比射线 1 传播半个波长。 对于垂直入射的射线,路径长度差为 2 t。
解决方案
为了在这里获得破坏性干扰,
\[2t = \dfrac{\lambda_{n2}}{2} \nonumber \]
其中\(\lambda_{n2}\)是胶片中的波长,由下式给出\(\lambda_{n2} = \lambda / n_2\)。 因此,
\[2t = \dfrac{\lambda/n_2}{2}. \nonumber \]
求解 t 并输入已知值得出
\[t = \dfrac{\lambda/n_2}{4} = \dfrac{(500 \, nm)/1.38}{4} = 99.6 \, nm. \nonumber \]
意义
当使用最薄的层时,例如本例中的薄膜在产生破坏性干扰方面最有效,因为入射角范围更广的光的强度会降低。 这些薄膜被称为非反射涂层;但是,这只是一个近似正确的描述,因为其他波长仅被部分取消。 非反射涂层也用于车窗和太阳镜。
将路径长度差与相位变化相结合
当两条射线的路径长度差为整数波长或半积分波长时,薄膜干涉最具建设性或破坏性最大。 也就是说,对于垂直入射的射线,
\[2t = \lambda_n, \, 2\lambda_n, \, 3\lambda_n, ... \, or \, 2t = \lambda_n/2, \, 3\lambda_n/2, \, 5\lambda_n/2, ... \nonumber \]
要知道干扰是建设性的还是破坏性的,还必须确定反射时是否有相位变化。 因此,薄膜干涉取决于薄膜厚度、光的波长和折射率。 对于入射在厚度不同的薄膜上的白光,随着厚度的变化,您可以观察到不同波长下构造干扰的彩虹色。
- 对波长为 650 nm 的红光产生构造干扰的肥皂泡最小的三个厚度是多少? 肥皂的折射率被认为与水的折射率相同。
- 哪三个最小的厚度会产生破坏性干扰?
策略
使用图形\(\PageIndex{3}\)可视化气泡,它充当两层空气之间的薄膜。 因此\(n_1 = n_3 = 1.00\)适用于空气,也\(n_2 = 1.333\)可用于肥皂(相当于水)。 从气泡顶部表面反射的射线 1 有 λ/2 偏移,而从底部表面反射的光线 2 没有偏移。 因此,要获得构造干扰,路径长度差 (2 t) 必须是波长的半整倍数——前三个是\(\lambda_n/2, \, 3\lambda_n/2\)和\(5\lambda_n/2\)。 要获得破坏性干扰,路径长度差必须是波长的整数倍数——前三个是 0\(\lambda_n\)、和\(2\lambda_n\)。
解决方案
a. 此处发生建设性干涉的情况是
\[2t_c = \dfrac{\lambda_n}{2}, \, \dfrac{3\lambda_n}{2}, \, \dfrac{5\lambda_n}{2}, ... \nonumber \]
因此,最小的构造厚度\(t_c\)为
\[t_c = \dfrac{\lambda_n}{4} = \dfrac{\lambda/n}{4} = \dfrac{(650 \, nm)/1.333}{4} = 122 \, nm. \nonumber \]
产生构造干扰的下一个厚度是\(t'_c = 3\lambda_n/4\),这样
\[t'_c = 366 \, nm. \nonumber \]
最后,产生构造干扰的第三个厚度是\(t'_c = 5\lambda_n/4\)
\[t'_c = 610 \, nm. \nonumber \]
b. 对于破坏性干扰,此处的路径长度差是波长的整数倍数。 第一种情况发生在厚度为零的情况下,因为顶部表面有相变,也就是说,
\[t_d = 0, \nonumber \]
上面讨论的非常薄弱(或可以忽略不计)的案例。 第一个产生破坏性干扰的非零厚度是
\[2t'_d = \lambda_n. \nonumber \]
替换已知值可以得出
\[t'_d = \dfrac{\lambda}{2} = \dfrac{\lambda/n}{2} = \dfrac{(650 \, nm)/1.333}{2} = 244 \, nm. \nonumber \]
最后,第三个破坏性厚度是\(2t''_d = 2\lambda_n\),所以
\[t''_d = \lambda_n = \dfrac{\lambda}{n} = \dfrac{650 \, nm}{1.333} = 488 \, nm. \nonumber \]
意义
如果用纯红光照亮气泡,我们会看到亮带和暗带的厚度都非常均匀地增加。 首先是厚度为 0 的暗带,然后是厚度为 122 nm 的亮带,然后是 244 nm 处的暗带,366 nm 处的亮带,488 nm 处的亮带,610 nm 处的亮带。 如果气泡的厚度变化平滑,比如光滑的楔子,那么带子间隔将均匀。
再举个例子\(\PageIndex{2}\),接下来的两个肥皂泡会导致什么厚度的肥皂泡
- 建设性干预,以及
- 破坏性干扰?
- 回答 a
-
853 nm 和 1097 nm
- 答案 b
-
731 nm 和 975 nm
另一个薄膜干扰的例子是显微镜载玻片分离时(见图\(\PageIndex{4}\))。 滑块非常平坦,因此它们之间的空气楔的厚度会非常均匀地增加。 相变发生在第二个表面,但不是第一个表面,因此幻灯片接触的地方会形成一条暗带。 结构性干扰的彩虹色重复,随着幻灯片之间距离的增加,一次又一次地从紫色变为红色。 随着空气层的增加,波段变得越来越难以看清,因为入射角度的微小变化对路径长度差异的影响更大。 如果使用单色光而不是白光,则会获得亮带和暗带,而不是重复彩虹色。
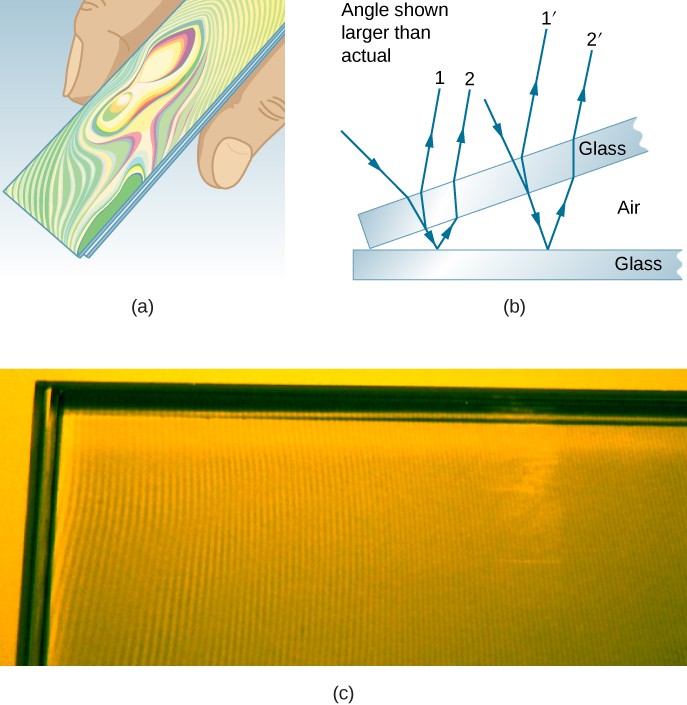
薄膜干涉的一个重要应用是在光学仪器的制造中。 镜头或反射镜在研磨时可以与主镜进行比较,从而使其在整个表面上精度小于一个波长。 该图\(\PageIndex{5}\)说明了称为牛顿环的现象,这种现象发生在两个镜头的平面表面放置在一起时。 (圆环之所以被称为牛顿环,是因为艾萨克·牛顿详细描述了它们及其用法。 牛顿没有发现它们;罗伯特·胡克发现了,牛顿不相信它们是光的波浪特征造成的。) 给定颜色的每个连续环表示镜头和空白之间的距离仅增加了半个波长,因此可以获得很高的精度。 一旦镜头变得完美,环形就不会出现。

薄膜干扰在自然界和制造业中还有许多其他应用。 由于薄膜干扰,某些飞蛾和蝴蝶的翅膀几乎呈虹彩色。 除了色素沉着外,机翼的颜色还受到薄膜涂层表面反射的某些波长的构造干扰的极大影响。 一些汽车制造商提供特殊的喷漆作业,这些作业利用薄膜干涉来产生随角度变化的颜色。 这种昂贵的选择基于薄膜路径长度随角度的差异而变化。 信用卡、纸币、驾驶执照和类似容易被伪造的物品上的安全功能使用薄膜干扰、衍射光栅或全息图。 早在1998年,澳大利亚就率先将美元钞票印在具有衍射光栅安全功能的聚合物上,这使得这种货币难以伪造。 其他国家,如加拿大、新西兰和台湾,也在使用类似的技术,而美元则包含薄膜干扰效应。


